Лекция 33

СПОСОБЫ КОНКРЕТНОГО РАСЧЕТА ФИЗИЧЕСКИ НЕЛИНЕЙНЫХ БАЛОК

Укажем один из способов решения уравнения изгиба физически-нелинейной балки:

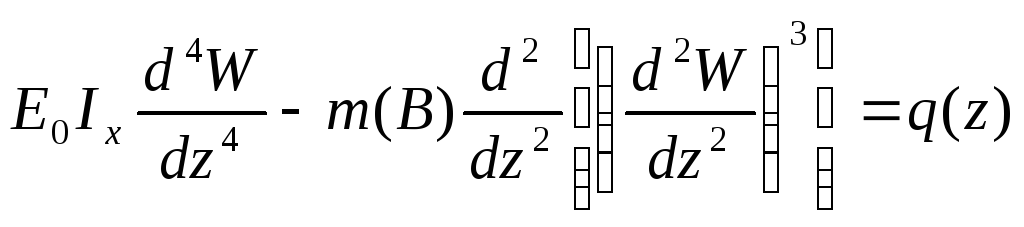(1) -обыкновенное нелинейное дифференциальное уравнение (т.к. во второе слагаемое входит В³)

E, m- постоянные

(3)-кубическая парабола

,

(1)- уравнение равновесия элементарной части балки.

Для задания конкретной задачи необходимо задать внешнюю нагрузку на балку и условие закрепления.

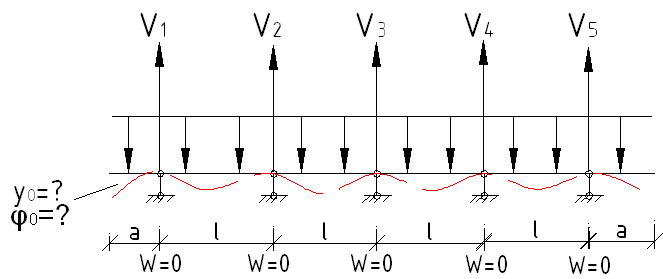
Граничные условия:

М(0)=0

Q(0)=0

• четыре граничных условия, полностью определяющих балку.

В задаче 7 неизвестных.

Для их нахождения используются условия:

Из решения замкнутой системы уравнений получаем величины семи неизвестных:

Тогда: (выражение для функции прогиба данной балки)

Для уравнения (1) предполагается, что:

(2)

Методы решения задачи:

1)Алгебраизация изгиба физически-нелинейной балки методом Бубнова-Галеркина.

Выражение (2) является приближенным выражением для функции прогиба.

При решении физически-нелинейной задачи с нелинейной связью напряжения-деформации (3) вид у(z) должен меняться.

Т.к. в строительных конструкциях допускаются небольшие пластические деформации, то на данном уровне деформирования считаем, что будет можно ввести коэффициент А уравнения (2)

РАСЧЕТ ФИЗИЧЕСКИ НЕЛИНЕЙНЫХ БАЛОК МЕТОДОМ БУБНОВА-ГАЛЕРКИНА

Используем алгебраизацию по методу Бубнова-Галеркина применительно к уравнению (1):

(4)

Подставляем (4) в (1): - в силу приближенности выражения (4)

Используем принцип Лагранжа:

Сумма работ системы всех внешних и внутренних сил на любом возможном и весьма малом перемещении равно нулю (обобщение принципа Лагранжа на физически-нелинейные системы).

- вариация прогиба балки.

(5)

Определенные интегралы от конкретных функций представляют собой числа, следовательно, после вычисления интегралов в (5) получаем:

(6)

Таким образом, от дифференциального нелинейного уравнения мы пришли к нелинейному алгебраическом уравнению (6).

РАСЧЕТ ФИЗИЧЕСКИ НЕЛИНЕЙНЫХ БАЛОК МЕТОДОМ КОНЧНЫХ РАЗНОСТЕЙ

Проводим алгебраизацию дифференциального уравнения (1) и граничных условий методом конечных разностей.

Для реализации метода конечных разностей по длине балки вводим сеть равноотстоящих узлов.

Для производных используем обычные формулы:

Тогда дифференциальное уравнении (1) и граничные условия записываются в виде системы линейных алгебраических уравнений.

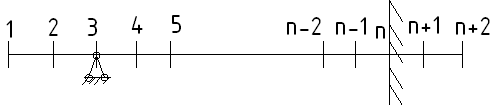
При числе участков разбиения длины балки порядка1000 обеспечивается точность вычислений по всем функциям порядка 0,1%, т.е. с помощью метода конечных разностей можно получить достоверные и весьма точные решения задач изгиба физически нелинейных балок.

Методы решения нелинейных дифференциальных уравнений

Практически реализуем следующий путь решения задачи:

1.предварительно привести уравнение к алгебраическому виду

2.решать данные алгебраические уравнения известными методами.

Рассмотрим метод простой итерации:

- нелинейное алгебраическое уравнение

Задача: построить нелинейную характеристику.

С ростом нагрузки интенсивность роста прогиба увеличивается

Рис.1

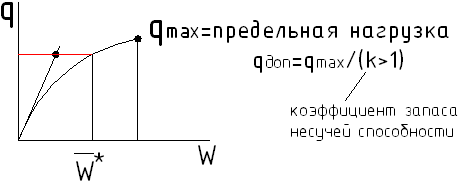
Наметим путь решения задачи:

- итерационная формула связи между предыдущим и последним значением А до сходимости (n=0,1,2,…)

- решение упругой задачи;

Доказательство:

Теорема о сходимости данного процесса, которая графически представляется в виде (рис 1)

Скорость сходимости метода простой итерации невысока.

Метод 2.

Рассмотрим уравнение:

Т.к. при , то величина А положительна (ищем в положительной области)

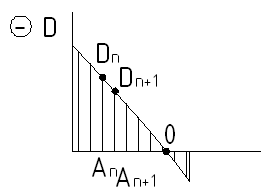
- условие перехода величины А через исходное значение.

Далее:

- смена знака шага и сбивания шага

Данная методика пригодна для линейного алгебраического уравнения любого порядка.

Метод упругих решений А. А. Ильюшина

Применим с любым методом алгебраизации задачи.

От уравнения (1) переходим к следующей записи:

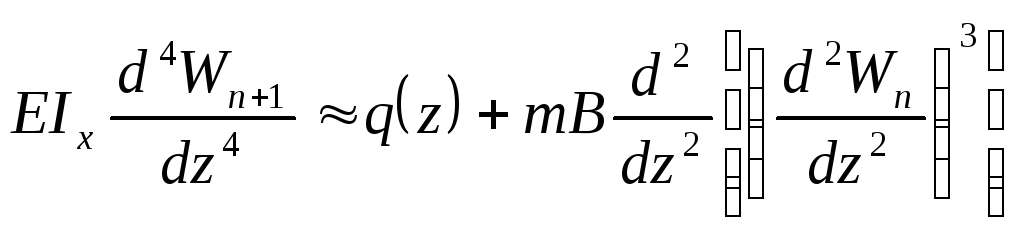, n=0,1,2,….

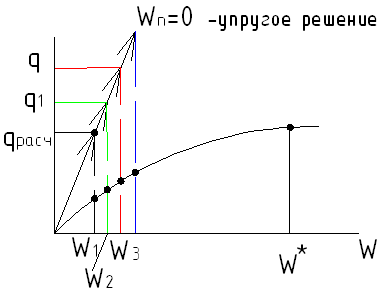
Правая часть полностью увеличивается, но разность между точками постоянно убывает

Метод переменных параметров упругости А. Биргера

Процесс сходимости является более быстрым, чем предыдущий. Графически процесс итераций имеет вид

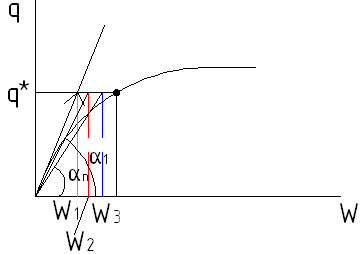
В этом случае дифференциальное уравнение используем в виде:

При движении к точному решению жесткостные параметры изменяются:

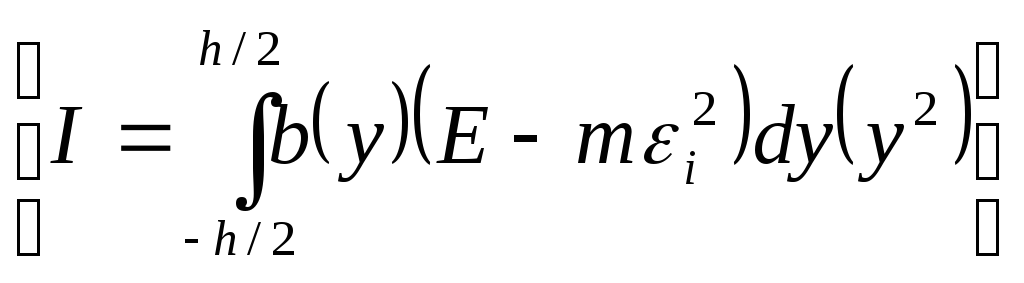- переменная жесткость, зависящая от уровня деформирования

При росте жесткость уменьшается (т.к. в скобках второе слагаемое увеличивается)

С учетом этого движение происходит под новым (меньшим) углом и процесс сходится быстрее, чем по методу упругих решений.

Метод Ньютона решения нелинейных алгебраических уравнений.

Предположим, что исходное деформированное уравнение алгебраизировано методом Бубнова-Галеркина или методом конечных разностей.

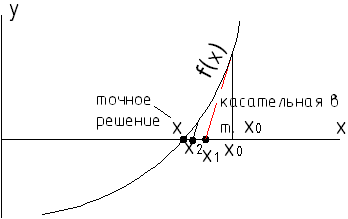
Выбираем начальное приближение к решению Х₀

Движения по касательным в точках Х_n

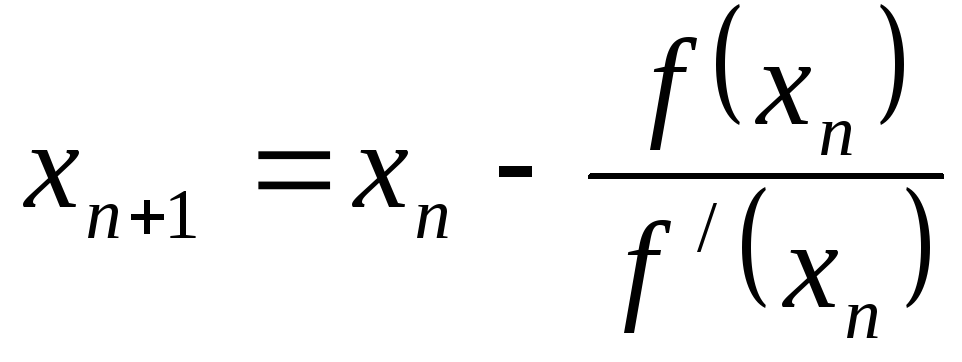, n=0,1,2,…

Скорость сходимости является квадратичной, т.е. очень высокой.

Этот метод применим к решению произвольной системы нелинейных алгебраических уравнений.

Шаговые методы решения нелегких задач. Метод последовательных нагружений.

Рассмотрим алгебраизованный аналог дифференциального уравнения (1)

(8)

Предположим, что при q=0, А=0- исходное недеформированное нагруженное состояние.

Разбиваем диапазон - на ряд малых степеней нагружени, например,

К уравнению (8) принимаем следующие возмущения

следует приращение значения нагрузки

(9) -точное выражение для исходного рассматриваемого состояния.

(*)

Подставляем (*) в (9)

(10)

Из (10) вычтем (9):

Далее повторяем процесс, т.е. получаем значения:

(т.е. вдоль кривой нагружения)