Лекция 30

Расчет пластинок методом Бубнова-Галеркина.

Записываем дифференциальное уравнение изгиба элемента пластинки:

(1)

Для конкретной задачи записывается по два граничных условия в каждой точке.

Записываем дифференциальное уравнение в безразмерном виде: при этом расчет одной пластины соответствует бесконечному множеству реальных пластин.

Вводим безразмерные переменные и функции по следующим формулам:

,

- безразмерный параметр прогиба; - толщина (м).

,

Подставляя данные формулы в уравнение (1):

/:

Вводим параметр

(2)

- дифференциальное уравнение изгиба пластинки в безразмерном виде.

При этом пластинка примет вид:

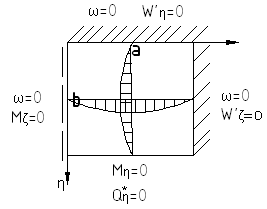
В безразмерном виде формулы для внутренних силовых факторов примут вид:

- безразмерный изгибающий момент в направлении оси ζ.

Для оси η:

-

В уравнении (2) справа от знака “=”- внешние силы, а слева- внутренние.

Принцип Лагранжа: Сумма работ всех внешних и внутренних сил упругой системы на любом возможном и бесконечно малом перемещении равно 0.

Возможные перемещения должны быть совместимы с граничными условиями задач.

Применяем принцип Лагранжа к уравнению (2).

Возможное перемещение обозначим: .

В методе Бубнова-Галеркина прогиб в первом приближении решения записаться в виде:

А- амплитуда прогиба, максимальное из решения задач по методу Бубнова-Галеркина.

Вариации прогиба записываются в виде:

- бесконечно малое изменение амплитуды прогиба.

(3)

В результате подстановки можно записать:

- функция с разделяющимися переменными

- функция с разделяющимися переменными

Тогда получаем следующие выражения:

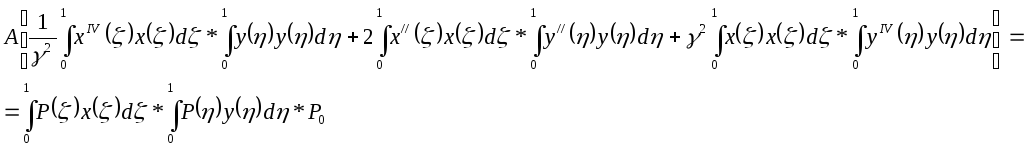
Т.к. функции иизвестны, то известны все величины определенных интегралов. После чего можно записать:

где _{и моменты инерции.}

После нахождения амплитуды прогиба все величины в пластинке подсчитываются по следующим формулам:

Аналогичные формулы для этих параметров используются методом Рицце - Тимошенко.

Рассмотрим пример:

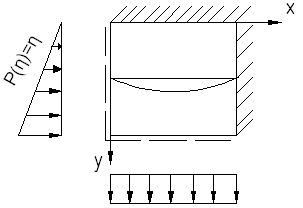
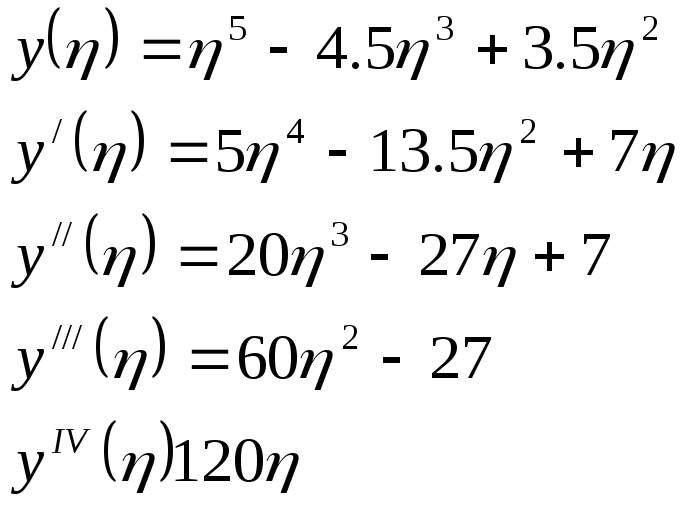
Получаем выражения для следующих производных функций

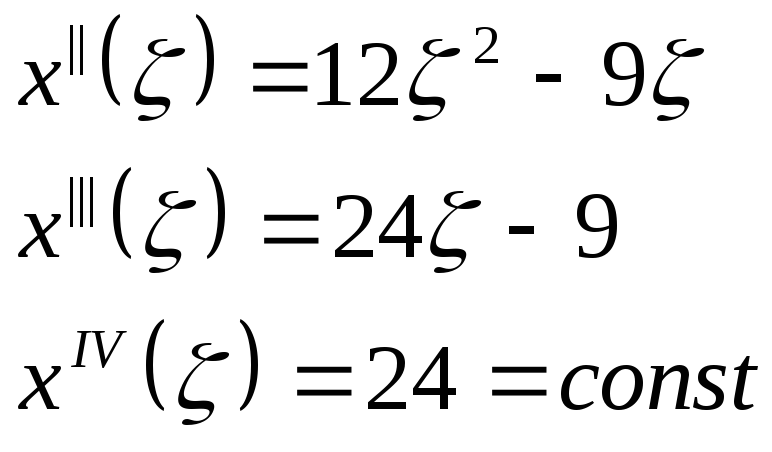
Подсчитаем интеграл:

Аналогично вычисляются интегралы I₁ и I₄.

в результате вычисления определенных интегралов получаются амплитуды прогибов А.

После этого необходимо посмотреть следующие эпюры:

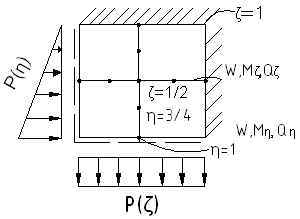
Чтобы не ошибиться, можно использовать ПЭВМ;

Можно записать:

WRITE (‘x=’); READLN (x);

WRITE (‘y=’); READLN (y);

WRITE (‘A=’); READLN (A);

MKS:=-A*((12*x*x-9*x)*(y*y*y+y*…)+MU*…)

WRITELN(‘MKS=’,MKS);

Лекция 31

Расчет пластинок методом Власова-Конторовича

Рассмотрим конкретную пластинку.

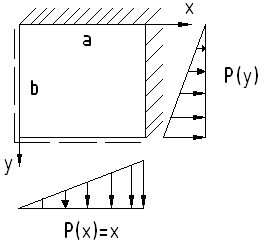
Входные данные: a, b, h, E, μ.

Условие закрепления пластинки (4)

Условие нагружения q(x,y) – аналогичная функция.

Если распределение q(x,y) сложное, то нагрузку следует разложить в ряд и получить решение на каждый член ряда. Затем полученное суммируется.

Расчет загружения половины плоскости. По нормам расчет ведется по загружению всей половины и четверти плоскости.

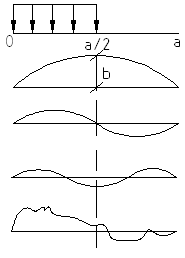
Удобнее решать задачу в безразмерном виде.

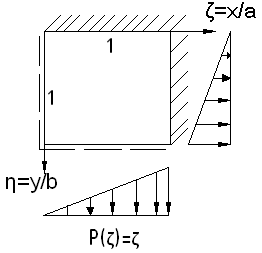
Входными параметрами являются:

Условие закрепления (4)

- функция с разделяющимися переменными

При этом необходимо записать в безразмерном виде дифференциальные уравнения изгиба пластин:

(1)

Необходимо записать граничные условия:

: ,- жесткое закрепление

Если шарнирное закрепление:

: ,

Т.к. сторона шарнирного закрепления остается прямой, то =>(2)

Шарнирное закрепление :,=>

: ,

В соответствии с методом Власова-Канторовича запишем:

(3)

Одну из функций необходимо построить по методу В.З. Власова.

С₃=0, С₄=0

После этого функция становится полностью определенной.

Используем принцип Лагранжа.

Сумма работ внешних и внутренних сил упругости системы на любом возможном и бесконечно молом равно 0.

: заменено приближенным выражением.

- приближенное выражение.

- известная функция

- малое возмущение

Тогда получим:

Все величины, зависящие от η, могли быть получены из-под значения интеграла:

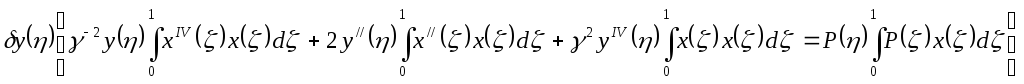(4)

Т.к. функция известна, то известны и величины определенных интегралов:

В результате из выражения (4) получается обыкновенное дифференциальное уравнение вида, дающая точное решение.

(5)

Если рассмотреть полное дифференциальное обыкновенное уравнение с переменными коэффициентами, то для решения можно использовать метод конечных разностей.

Т.к. (5) является неоднородным уравнением, то решение запишется в виде:

- решение неоднородного уравнения, определяемое правилом (5) (6)

(7)

Приходим к алгебраическому уравнению (характеристическому):

(8)

,

Решение получается в комплексном виде. Необходимо преобразовать его в вид:

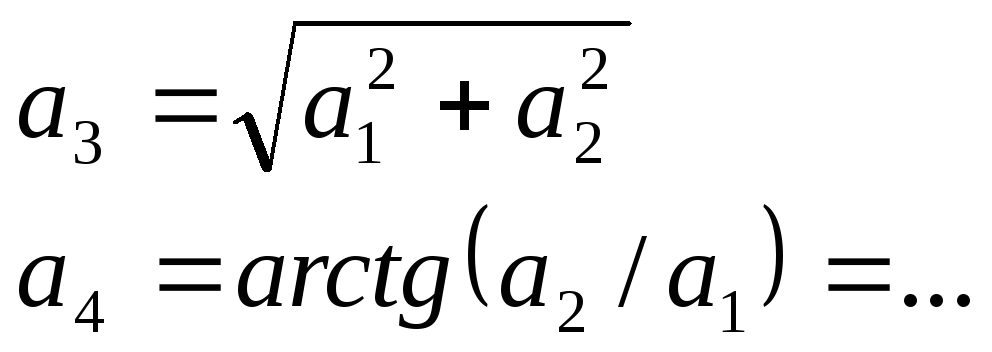
Тогда нужно подсчитать 2 величины:

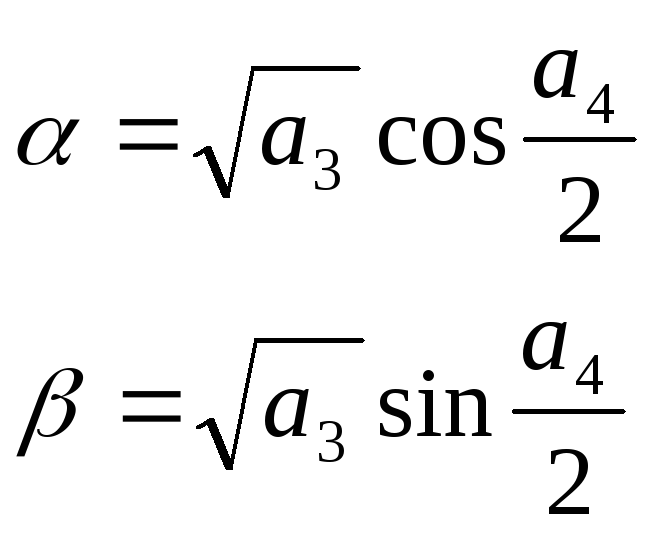
Тогда решение однородного уравнения запишется в виде:

После этого необходимо частное найти решение уравнения:

Т.к. нагрузка по оси η постоянна и , то

- число

Тогда общее решение:

_{Если реализуется случай Р(η)=η, то}

_{Остается найти произвольную постоянную интегрирования из условия закрепления пластинки по оси η}

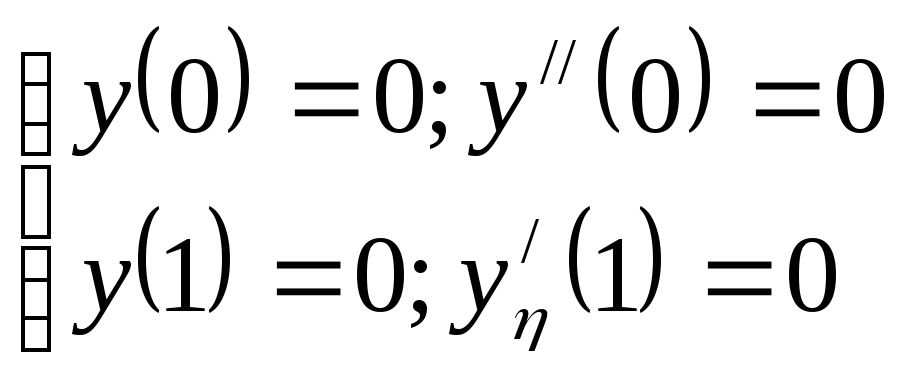
_{Получается система 4-х алгебраических уравнений относительно С1, С2, С3, С4, из которых находим эти величины.}

_{: ,}

_{Записываем выражение для производной функции у(η)}

_,,,,