Лекция 10

_{Изгиб балок}

_{Балкой называется как правило горизонтально расположенный прямолинейный стержень с определенным соотношением габаритов.}

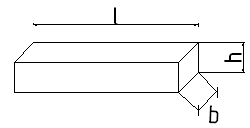
_{В сопротивлении материалов рассматриваются следующие опорные закрепления}

_{балок: шарнирно-подвижная опора, шарнирно-неподвижная опора, заделка (жесткое защемление).}

_{Нагрузки на балки делятся на: сосредоточенные силы P, сосредоточенные моменты M, распределенные по длине нагрузки q.}

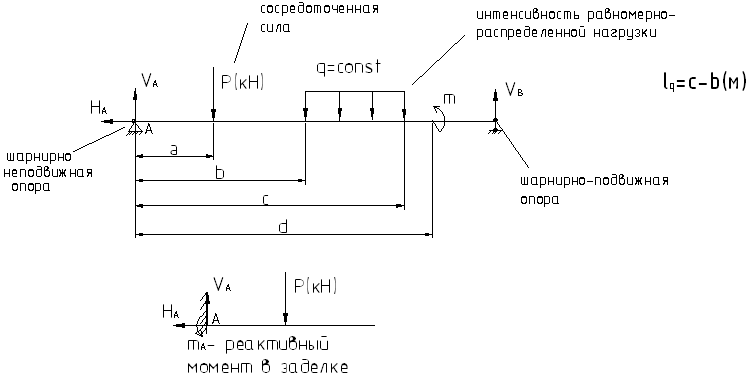
_{Проводим описание опытного исследования изгиба на образце балки.}

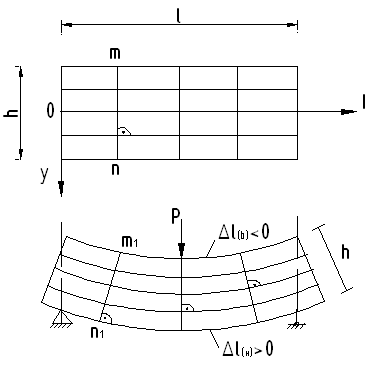
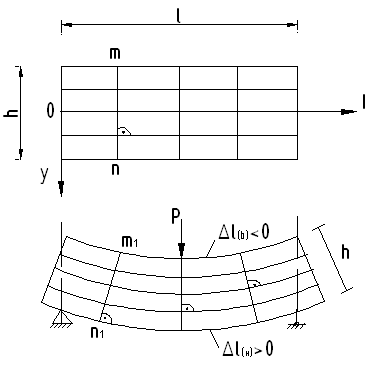
_{Из анализа деформированного состояния балки под нагрузкой можно установить следующее:}

1. _{В процесса нагружения высоты балки остается постоянной}

_h=const

_∆h=0

_{εy= ∆h/h=0}

₍₁₎

_{Т.к. h=const, то волокна по высоте балки не давят друг на друга (гипотеза Навье)}

_{2. При изгибе рассматриваемой на рис. балки верхние волокна укорачиваются, нижние волокна удлиняются, а волокна посередине высоты прямоугольного поперечного сечения балки сохраняют свою длину (нейтральные волокна)}

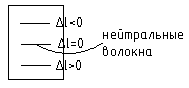
_{, (2)}

₍₃₎

• _{На эпюре продольных нормальных напряжений 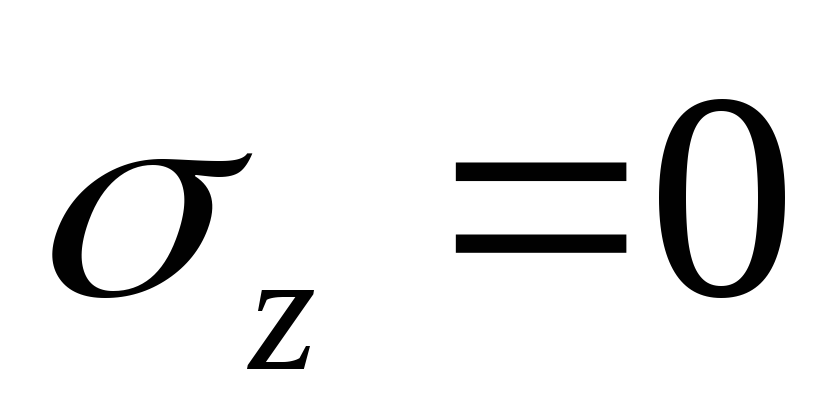на нейтральных волокнах балки}

_{3.При изгибе балок нормальный элемент mn остается прямым и перпендикулярным к бывшим горизонтальным прямым.}

_{- прямая (линейная зависимость)}

_{- линейная зависимость}

_{По гипотезам Навье σz меняются по высоте сечения балки по линейному закону}

_{\Из анализа формул (3) и (4) устанавливаем, что эпюра σz выглядит следующим образом.}

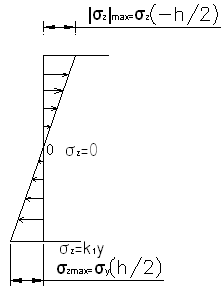
_{Вырежем из балки бесконечно малый элемент}

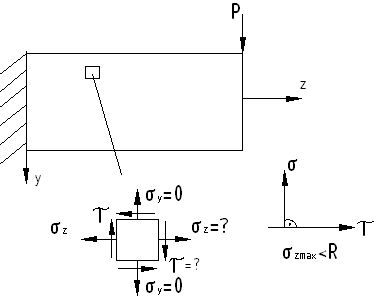
_{Rсреза – расчетное сопротивление материала на срез.}

_{Необходимо выявить внутренние силовые факторы в изгибаемой балке.}

_{Используем метод сечений РОЗУ:}

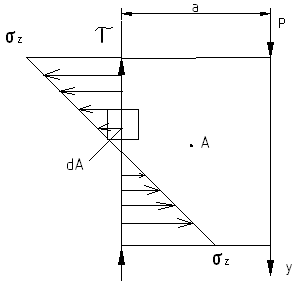
_{Условие несмещаемости по вертикали}

_{- поперечная сила}

_,

_{то есть Q можно найти через внешние силы, приложенные к балке.}

_{Определение (1): Поперечной (перерезывающей) силой Q (кН) в данном сечении балки называют внутренней силовой фактор , численно равный алгебраической сумме проекций на нормаль к оси балки всех сил, взятых по одну сторону от рассматриваемого сечения.}

_{Правило знаков для поперечной силы Q:}

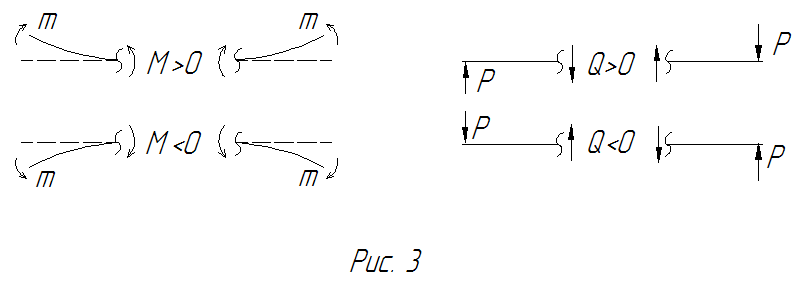
_{Q>0, если элемент балки вращается по часовой стрелке.}

_{Рассмотрим пример подсчета Q.}

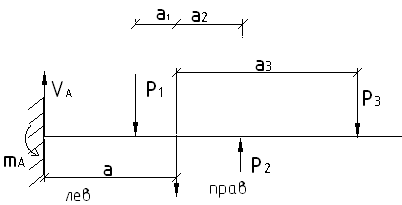
_{Рис. 1}

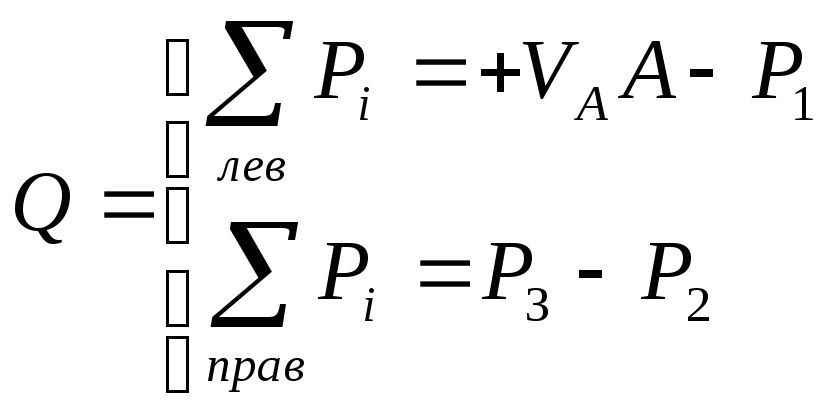
_{МА не входит в уравнение}

_.

_{Рассмотрим другой внутренний интегральный силовой фактор – изгибающий момент}

_{- изгибающий момент}

_{Итак, изгибающий момент может быть подсчитан двумя способами:}

_{Определение (2): Изгибающим моментом M(z) (кН*м) в данном сечении балки называют внутренний силовой фактор , численно равный в данном сечении балки алгебраической сумме моментов всех сил, взятых по одну сторону от рассматриваемого сечения.}

_{Правило знаков для изгибающего момента:}

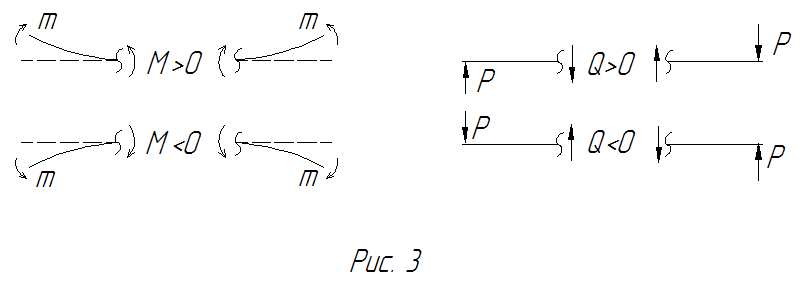
_{М>0, если при изгибе балки растягиваются нижние волокна}

_{По рисунку (1) вычисляем момент:}

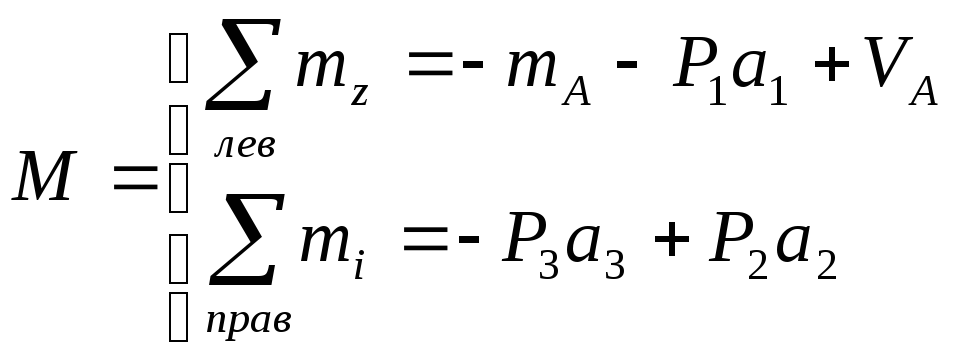
_{Существуют 9 фундаментальных правил взаимной проверки эпюр Q и M, основанные на теореме}

_{Д.И. Журавского:}

₍₁₎

₍₂₎

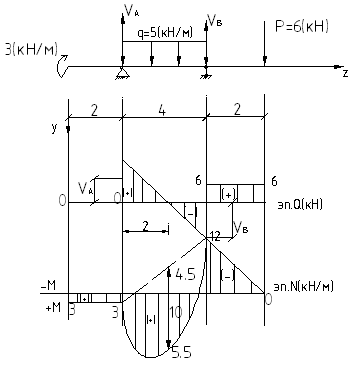
1. _{На участке балки без распределенной нагрузки q=0, Q=const, а момент меняется по закону прямой линии M=a+bz}

2. _{На участке балки c распределенной нагрузкой q=const, Q=a+bz - прямая, M=a1+b1z+c1z}² _{– парабола второй степени}

3. _{если на участке балки Qij>0, то Мправ>Mлев}

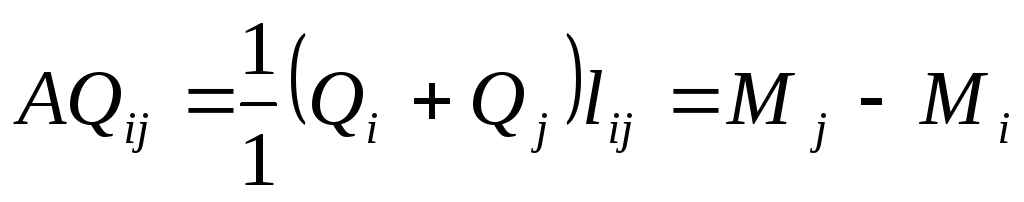4. _{- площадь эпюры Q на каждом участке балки равняется разности правой и левой ординат эпюры моментов M на данной участке.}

_{5., - экстремальная ордината на эпюре М соответствует нулевому значению на эпюре Q}

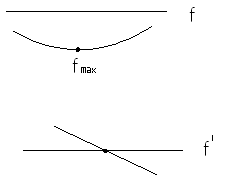
_{6.На эпюре Q под каждой сосредоточенной силой реализуется скачок на величину данной силы по направлению данной силы}

7. _{На эпюре М под каждым сосредоточенным моментом Mj реализуется скачок на величину Мj.}

8. _{Если на эпюре изгибающих моментов +М – снизу, а –М – сверху, то направление распределенной нагрузки q указывает направление выпуклости на эпюре М.}

9. _{Направление каждой сосредоточенной силы Рм указывает направление излома на эпюре М.}