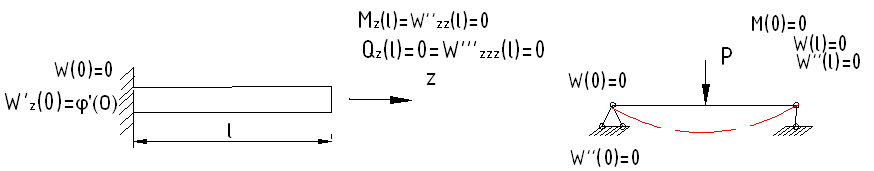- •Классификация объектов мдтт:
- •Гипотезы сопротивления материалов.
- •Принцип относительной жёсткости.
- •Лекция 2
- •Лекция 3 Расчет ступенчатого бруса
- •Лекция 4
- •Лекция 5
- •Лекция 6
- •Лекция 7
- •Лекция 8
- •Лекция 9
- •Лекция 10
- •Лекция 11
- •Лекция 12
- •Лекция 13
- •Лекция 14
- •Лекция 15
- •Лекция 16 балки на упругом основании
- •Составление уравнения прогибов y (z), углов поворота φ (z), изгибающих моментов м(z) и поперечных сил q(z)
- •Лекция 17 определение начальных параметров y0, φ0, m0, q0 из условий закрепления балки по концам
- •Построение эпюр y (z), φ (z), m (z), q (z) и реактивных давлений r (z)
- •Лекция 18
- •Внецентренное сжатие стержней.
- •Лекция 19
- •Лекция 20
- •Лекция 21
- •Лекция 22
- •Лекция 23
- •Лекция 24 Продольно-поперечный изгиб
- •Лекция 25
- •Лекция 26 Техническая теория изгиба пластин
- •Классификация пластинок
- •Упрощающие гипотезы теории пластин средней толщины
- •Лекция 27 вывод уравнения равновесия для элементарной части пластины
- •Виды граничных условий
- •Лекция 28
- •Лекция 29
- •Лекция 30
- •Лекция 31
- •Лекция 32
- •Лекция 33
- •Лекция 34
- •Явление усталости
- •Явление ползучести. Длительная прочность
- •Презентации
- •Учебные пособия
- •Видео-материалы
- •Список рекомендуемой иностранной литературы
- •2.2 Методические указания по проведению лабораторных работ
- •2.3. Методические указания по выполнению кр/кп
- •2.4. Методические указания по организации самостоятельной работы студента (срс)
- •2.5. Методические указания по выполнению ргр
- •Методические указания по курсу сопротивления
- •Тесты (прилагаются отдельным файлом)
- •Контрольные вопросы
- •Папка 4. Информационные материалы по дисциплине Выписка из Государственного образовательного стандарта
- •До изучения курса «Сопротивление материалов» студент должен изучить курс Высшей математики и курс Теоретической механики.
- •Министерство образования и науки Российской Федерации
- •3.Распределение трудоемкости (час) дисциплины по темам и видам занятий.
- •4.Содержание лекционного курса.
- •5. Перечень практических занятий
- •6. Перечень лабораторных работ.
- •7.Занятия для самостоятельной работы студентов.
- •8. Курсовой проект.
- •Экзаменационные вопросы.
- •13.Список основной и дополнительной литературы по дисциплине.
- •13.1 Основная литература.
- •13.2.Дополнительная литература
- •14.Использование наглядных пособий, тсо, вычислительной техники.
- •15.Дополнения и изменения в рабочей программе Рабочая программа пересмотрена на заседании кафедры
Лекция 32
Теории пластичности
Диаграмма деформирования пластичного материала.
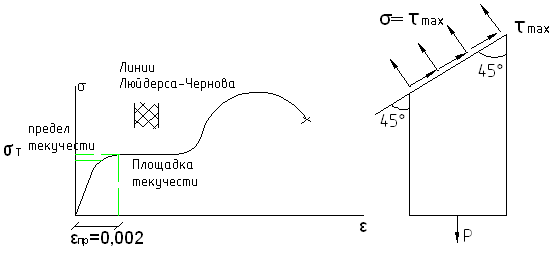
Для расчета стальных конструкций пластичную диаграмму заменяют условной диаграммой Прандтля.
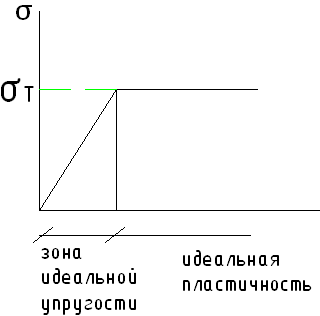 -
идеально упругое пластичное тело
-
идеально упругое пластичное тело

В зависимости от рассматриваемого материала (реального) выбирается та или иная (из условия совпадения теоретического материала данного опыта).
Для многих материалов диаграмма деформирования является не линейной.
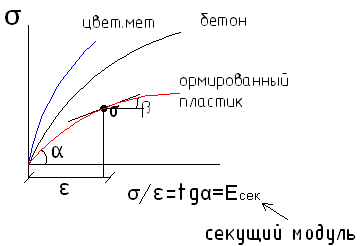
Поэтому
возникает необходимость математическое
описание зависимости
![]() .
.
Существуют апробированные формы:
![]() ,
,
![]() (1)
–степенная
зависимость с двумя коэффициентами а
и k.
(1)
–степенная
зависимость с двумя коэффициентами а
и k.
Коэффициенты подбираются из наилучших соответствий теоретической кривой и опытных результатов.
![]() (2)
– кубическая
парабола
(2)
– кубическая
парабола
![]() (Па)-
касательный модуль
(Па)-
касательный модуль
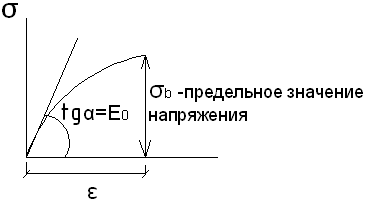
Вычисляем величину секущего и касательного модулей:
![]()
![]()
Используем два условия:
1)при
![]()
![]() - начальный модуль материала.
- начальный модуль материала.
![]()
В начальном участке деформирования траектория совпадает с упругой траекторией.
Для подсчета второго коэффициента используем условие:
![]() ,
,
![]() ,
что соответствует точке графика
,
что соответствует точке графика![]()
Тогда:
![]()
![]() Па
– величины констант получаются в [Па]
Па
– величины констант получаются в [Па]
Тогда формула имеет вид:
![]()
Теорию пластичности можно построить лишь путем введения определенных гипотез.
Вспомним термины, относящиеся к напряженному деформированному состоянию тела:
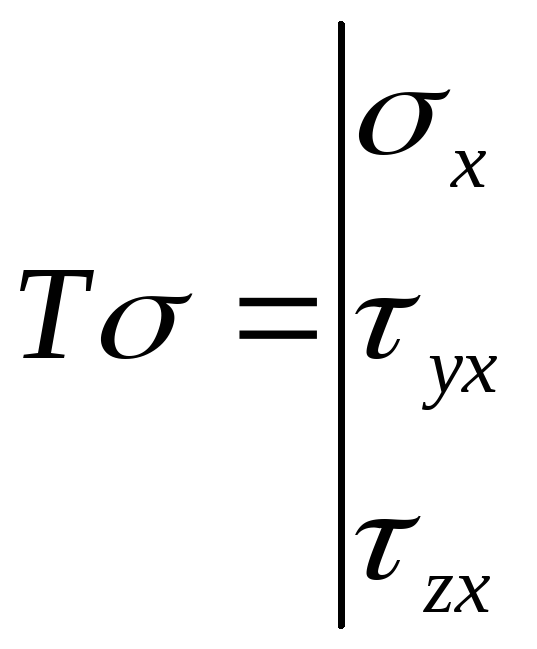
![]()
![]() -
тензор напряжения (тензор второго ранга)
-
тензор напряжения (тензор второго ранга)

![]()

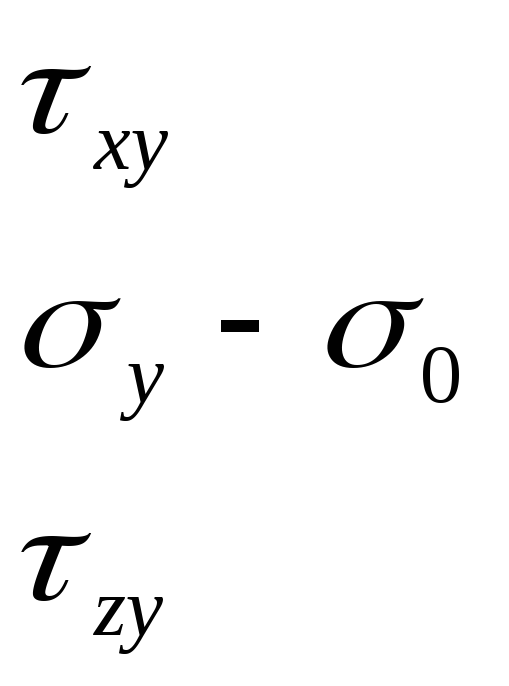
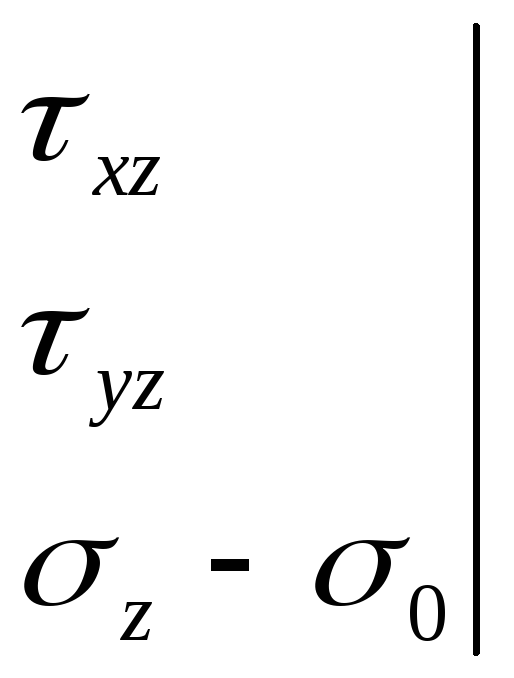
Среднее
нормальное напряжение в данной точке:
![]()
Для деформированного состояния вводим аналогичные величины:
![]()
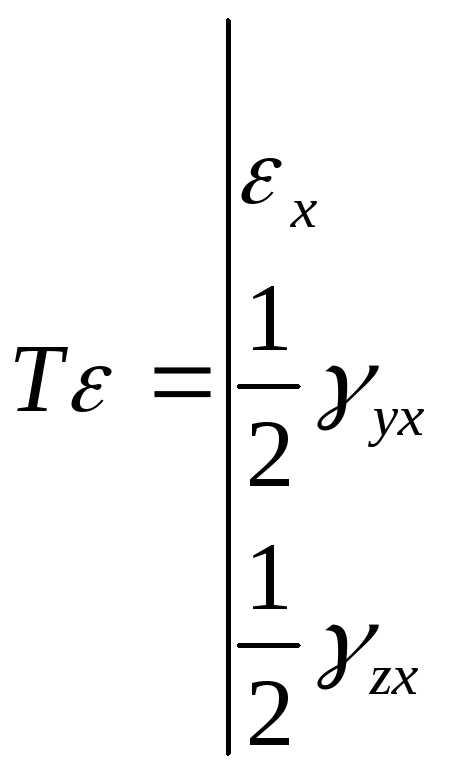
![]()
 -
тензор деформации (второго ранга)
-
тензор деформации (второго ранга)

![]()
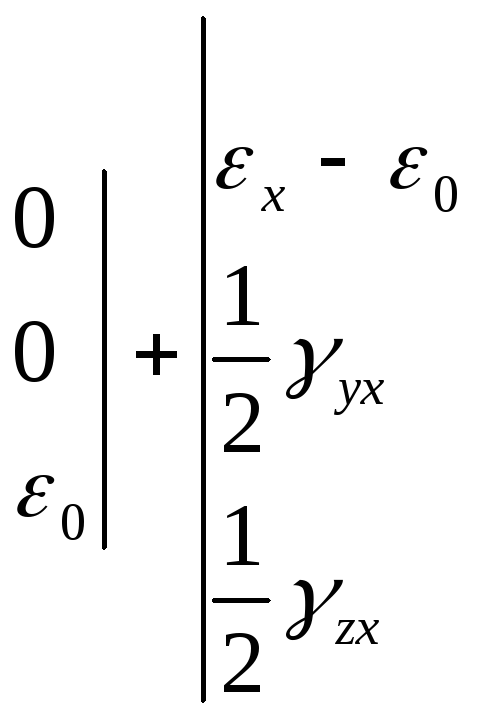
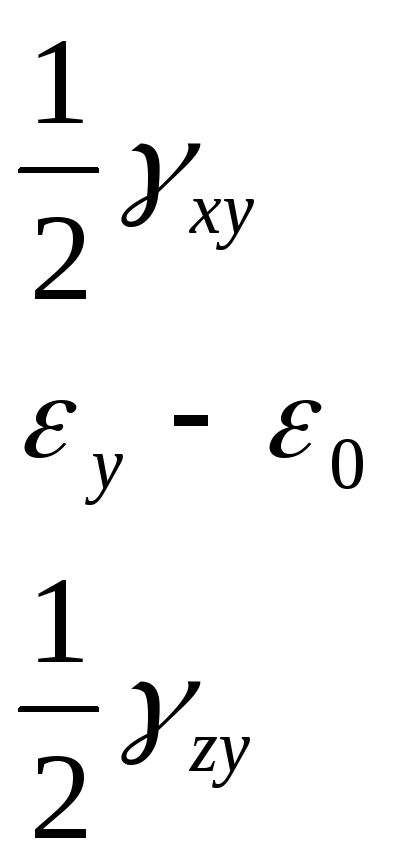
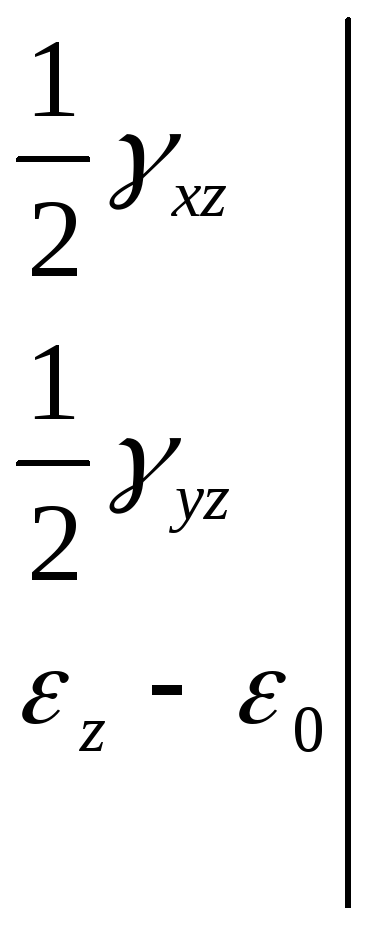
Средняя
линейная деформация в данной точке
тела:
![]()
Теория малых упруго-пластических деформаций А.А. Ильюшина
Данная теорема базируется на трех законах:
1)Закон изменения объема тела.
Изменен6ие объема происходит по линейному закону в следующем виде:
![]()
k - объемный модуль данного материала.
![]()
2)Закон изменения формы:
Изменение формы определяется дивиаторами напряжения и деформации:
![]() пропорциональная
зависимость между дивиаторами.
пропорциональная
зависимость между дивиаторами.
Подобие между напряжениями и деформационными состояниями изменения формы
![]()
![]()
![]()
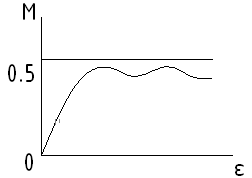
3)Закон
о единой кривой деформирования
![]() :
для
любого вида напряженного состояния
тела (одномерного, двухмерного,
трехмерного) существует единая зависимость
:
для
любого вида напряженного состояния
тела (одномерного, двухмерного,
трехмерного) существует единая зависимость![]() ,
причем функцияf
совпадает стыковой зависимостью
,
причем функцияf
совпадает стыковой зависимостью
![]() при простом испытании материала.
при простом испытании материала.
К простому испытанию относится испытание на растяжение, сжатие, изгиб.
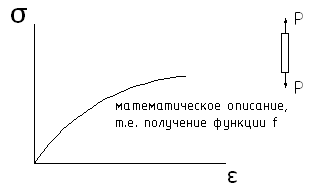
Затем, после получения функции f она применяется для любых типов напряженного состояния тела.
Как правило, при использовании теоремы Ильюшина вводят дополнительные упрощающие напряжения.
Обычно
предполагается
![]() ,
следовательно несжимаем материал (для
стержней, пластинок, оболочек значительно
легче вызвать изменение формы, чем
оббьем)
,
следовательно несжимаем материал (для
стержней, пластинок, оболочек значительно
легче вызвать изменение формы, чем
оббьем)
Запишем:
![]() ,
,![]() ,
,![]() ,
,![]()
![]() -
коэффициент Пуассона для несжимаемого
материала.
-
коэффициент Пуассона для несжимаемого
материала.
Тогда формула следует из второго закона:
 -более
простые формулы
-более
простые формулы
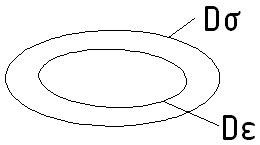
Траектория
![]() и
и![]() подобны и у них совпадает главные оси.
подобны и у них совпадает главные оси.
УРАВНЕНИЕ ИЗГИБА БАЛКИ ИЗ ФИЗИЧЕСКИ НЕЛИНЕЙНОГО МАТЕРИАЛА
Рассмотрим
балку из материал с нелинейной зависимостью
![]()
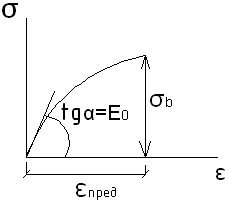
![]() -
кубическая парабола
-
кубическая парабола
![]()
![]()
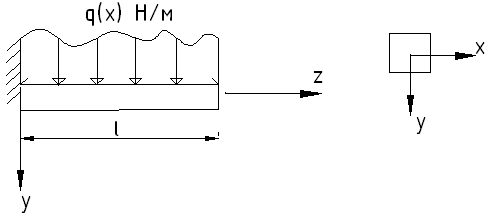
По теореме Журавского:
![]()
Возникает задача записи выражения для изгибающего момента М(z). При этом используются формулы для:
![]() -
нормальное напряжение по продольному
направлению вертикального деформирования
-
нормальное напряжение по продольному
направлению вертикального деформирования
![]() ;
;
![]()
![]() -
волокна по высоте балки не давят друг
на друга.
-
волокна по высоте балки не давят друг
на друга.
![]() -
деформирование по толщине балки
-
деформирование по толщине балки
![]() -
поперечный габарит балки остается
постоянным
-
поперечный габарит балки остается
постоянным
![]()
![]()
![]()
Для
несжимаемого материала
![]()
Тогда:
![]() -
для упругой задачи.
-
для упругой задачи.
Для балки при нелинейной зависимости будем иметь:
![]()
Выражение деформирования через прогиб балки:
![]() (совпадает
с изменением
(совпадает
с изменением
![]() в упругой балке)
в упругой балке)
Тогда выражение для момента имеет вид:
![]()

Подставляем в данную формулу следующие величины:
![]()
Тогда
изгибающий момент:
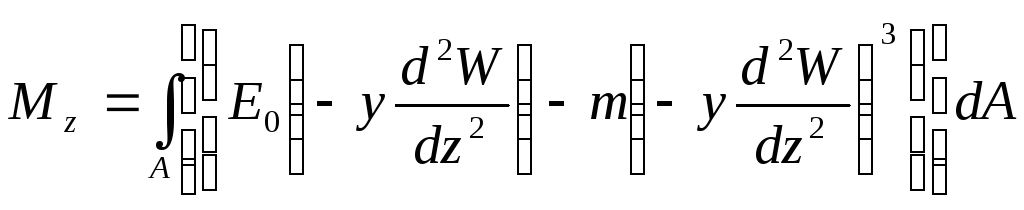
Рассмотрим балку прямоугольного поперечного сечения:
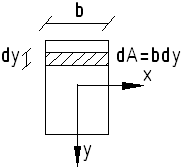
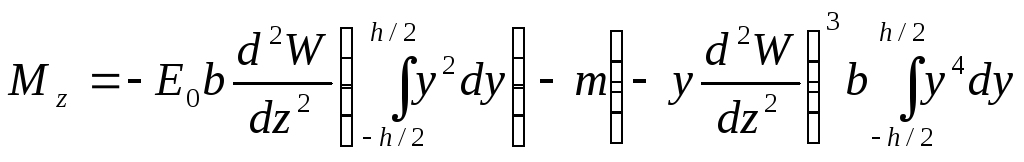
Подсчитаем величины:
![]() -момент
инерции поперечного сечения
-момент
инерции поперечного сечения
![]() -геометрическая
характеристика высшего порядка
-геометрическая
характеристика высшего порядка
Тогда выражение для изгибающего момента имеет вид:
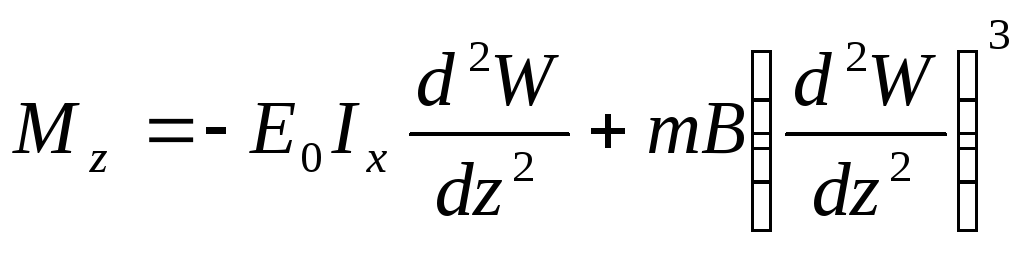
![]() подставим
в формулу Журавского:
подставим
в формулу Журавского:
![]()
Тогда:
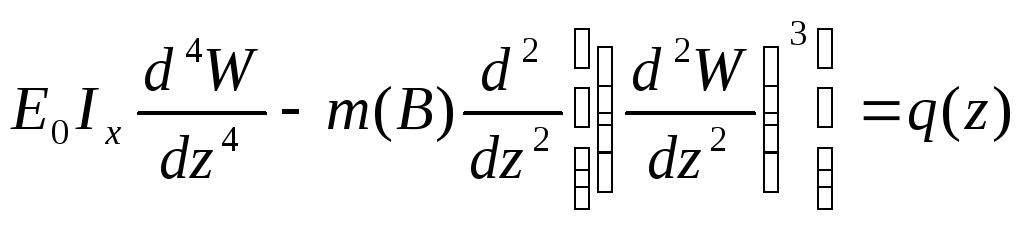 (1)
(1)
Для упругой балки получаем:
![]()
Уравнение (1) соответствует уравнению равновесия элемента балки под действием распределенной нагрузки q с учетом нелинейной зависимости деформации.
Для конкретизации задачи необходимо задать
1)q(z)
2)граничные условия по концам балки: