Лекция 23

Расчет изгибаемых балок с тонкостенным поперечным сечением

на стестенное кручение

При обычном изгибе балки используется функция у(м)- прогиб

у(м) –прогиб - участок закручивания (рад)

- угол поворота - искривление поперечного сечения стержня)

- изгибающий момент - бимомент

- изгибный момент

При кручении тонкостенного профиля возникает крутящий момент:

(1) - составляющая крутящего момента

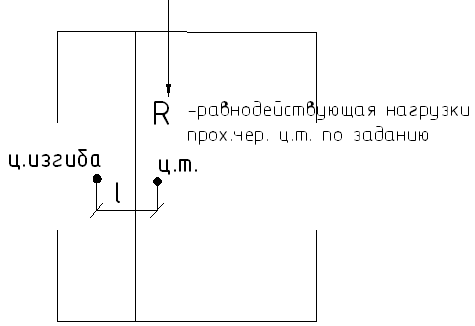
В результате возникает крутящий момент:

- расстояние от центра изгиба до центра точки

- секториальный момент площади при полюсе в центре изгиба.

Приводим уравнение (1) к виду:

Дифференцируем уравнение (1): - погонное колебание

(2)

Вводим обозначения: ;(3)

- может быть решено методом начальных параметров в соответствии с граничными условиями по концам балки.

Два начальных параметра определяются сразу из условий на левом конце балки, другой начальный параметр подсчитывается из системы уравнений, записанных для правого конца балки.

Нагрузка занимает всю балку целиком.

Тогда по методу начальных параметров выражения для функций будут иметь вид:

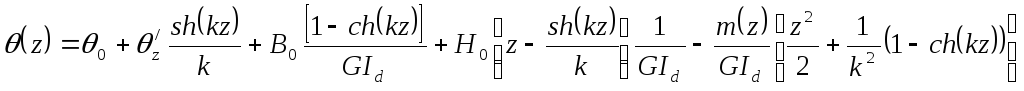
Все остальные функции получаются дифференцированием приведенного выражения

Рассматриваем вновь следующее поперечное сечение:

Ранее были подсчитаны следующие геометрические характеристики

, ,,,

, ,,,

,

Принимая (Н/м);(Нм/м)

Для трех схем:

1й случай:

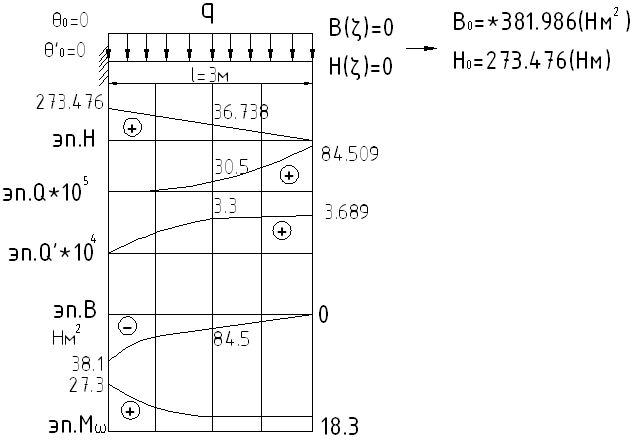
Угол закручивания зависит от k.

2й случай:

Эпюра получается разворотом предыдущей эпюры при частичной смене знаков.

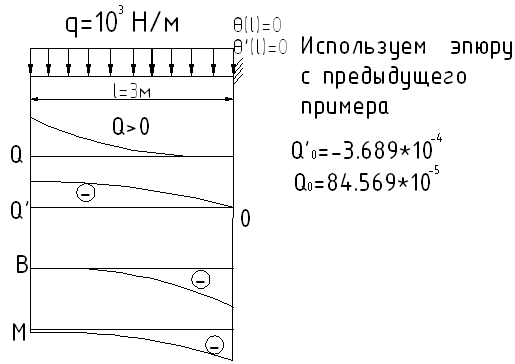
3й случай:

Затем необходимо построить следующие эпюры нормальных напряжений в поперечном сечении балки:

Сечения, где действуют идля всех типов закрепления балок совпадает, т.е. возможно рассмотреть следующие сечения:

Показываем характерный вид составленных эпюр у

В качестве точки, где выбрана берем точку О

При

Лекция 24 Продольно-поперечный изгиб

Рассмотрим шарнирно опертую по концам балку (рис.1), которая находится под действием поперечной нагрузки и централь­но приложенной силы Р.

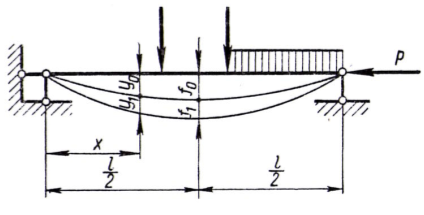
Рис. 1

Допустим, что сначала действовала только поперечная нагрузка, которая вызвала изгиб балки. Обозначим через у₀ и М₀ прогиб и изгибающий мо­мент в любом сечении бал­ки и примем это состоя­ние за начальное.

Приложим теперь к стержню, имеющему предварительное начальное искривление, сжимающую силу Р, тогда балка изогнется еще больше и прогиб б каждом сечении увеличится на величину y₁. Полный прогиб ее в любом сечении

у = у₀ + у₁

Величина полного прогиба будет плечом для сжимающей силы Р, следовательно, в каждом сечении балки помимо момента М₀ от действия поперечной нагрузки появится момент М_г от силы Р:

М₁=Ру=Р(у₀+у₁). (1)

Обозначим кривизну балки от действия поперечной нагрузки через 1/₀. Так как сжимающая сила увеличивает изгиб балки, то общая кривизна балки от действия поперечной нагрузки и сжимаю­щей силы Р будет 1/. Значит, приращение кривизны, вызываемое сжимающей силой Р, составит

. (2)

Так как приращение кривизны вызвано изгибающим момен­том М₁, то кривизна 1/₁ и изгибающий момент М₁ оказываются связанными соотношением

. (3)

Выразим приращение кривизны через вторую производную от приращения прогиба у₁:

.

Подставив кривизну 1/₀ и изгибающий момент М₁ в формулу (3), получим

_.

Перенесем неизвестные в этом уравнении в левую часть и, обозначив k²=P/EJ, запишем дифференциальное уравнение продольно-поперечного изгиба:

. (4)

Это уравнение полностью совпадает с уравнением, запи­санным для стержня, имеющего небольшое начальное искривление. Правая часть его у₀=у₀ (х) представляет собой изогнутую ось балки от действия поперечной нагрузки.

Таким образом, составлению дифференциального уравнения продольно-поперечного изгиба должен предшествовать расчет, в результате которого находится изогнутая ось балки от действия поперечной нагрузки.

Предположим, что изогнутая ось балки найдена. Тогда, под­ставляя выражение у₀=у₀ (х) в правую часть уравнения (4) и производя интегрирование, найдем приращение прогибов у₁ и изгибающих моментов М₁ в любом сечении балки от действия сжимающей силы. Складывая изгибающий момент М₁ от силы Р с изгибающим моментом М₀ от поперечной нагрузки, найдем пол­ный изгибающий момент в любом сечении стержня.

Решение задачи можно значительно упростить, если предста­вить изогнутую ось балки от поперечной нагрузки в силу ее поло­гости в виде полуволны синусоиды со стрелой, равной максималь­ному прогибу балки:

.

Предположим также, что дополнительные прогибы у в каждом сечении балки от действия сжимающей силы Р распределяются по закону синуса:

.

Подставляя принятые приближенные решения в уравнение (4), получим

.

Отсюда найдем стрелу прогиба f₁:

.

Это решение полностью совпадает с решением задачи о стержне, имеющем небольшое начальное искривление. Поэтому запишем сразу оконча­тельную формулу для вычисления полного прогиба в середине стержня:

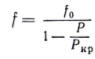. (5)

Изгибающий момент в любом сечении стержня от действия сжи­мающей силы Р определим по формуле

.

Проверка стержня на прочность производится по наибольшему изгибающему моменту. Для этого сначала найдем наибольший изгибающий момент М₀ от действия поперечной нагрузки и опре­делим сечение, в котором действует этот момент. Пусть это сечение будет х=с. Затем определим изгибающий момент М₁ в этом сечении от действия сжимающей силы Р:

.

Складывая эти моменты, найдем полный изгибающий момент в этом сечении

М = М₀+М₁.

При проверке на прочность нужно потребовать, чтобы напря­жения в крайних волокнах наиболее опасного сечения не превы­шали допускаемых:

.

Пример 1: Балка длиной l=4 м загружена в середине пролета вертикальной силой Р=10 кн и сжимается центрально приложен­ной силой P₁=150 кн (рис. 2). Подобрать сечение в виде дву­тавра, материал — Ст. 3.

Решение: Сначала подберем сечение из условия попереч­ного изгиба. Максимальный изгибающий момент в середине про­лета

Определим требуемый момент сопротивления:

По сортаменту нужно принять двутавр № 36. Однако, учитывая неблагоприятное влияние сжимающей силы, примем сечение с не­которым запасом: двутавр № 40, .F=71,4 см², J_у=666 см⁴, W_у==85,9 см³, i_y=3.05 см.

Рис.2.

Проверим подобранное сечение на устойчивость в плоскости наименьшей жесткости. Гибкость стержня

Выпишем значения коэффициентов :

при =130 = 0,40;

при = 140 =0,35.

Вычислим значение  для Х= 131,1:

Допускаемая сжимающая сила

Так как сжимающая сила принята Р₁=150 кн, то устойчивость стержня обеспечена.

Проверим теперь фактические напряжения в крайних волокнах наиболее опасного сечения. Максимальный прогиб в середине стержня от поперечной нагрузки

Для того чтобы вычислить полный прогиб, найдем сначала величину критической силы

Полный прогиб в середине стержня

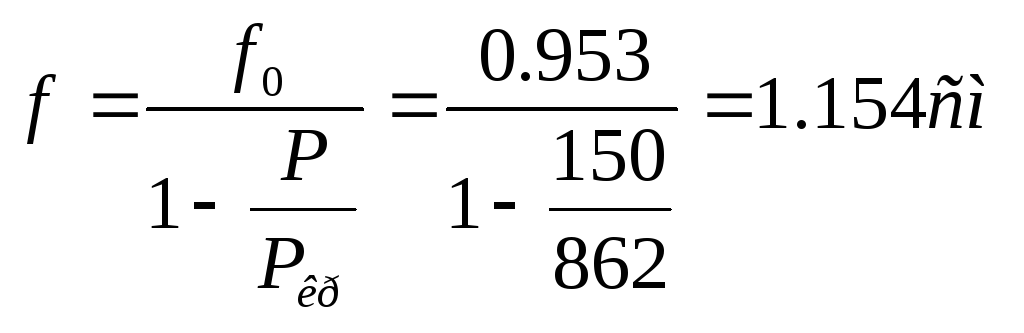
Вычислим дополнительный изгибающий момент от действия сжимающей силы:

Полный наибольший изгибающий момент и в середине стержня

М = М₀ + М₁=10+1,73=11,73 кнм.

Определим наибольшие сжимающие напряжения:

Подобранное сечение удовлетворяет условию прочности.