Лекция 4

Рассмотрим конкретный пример расчета стержня

1. V_A=? :

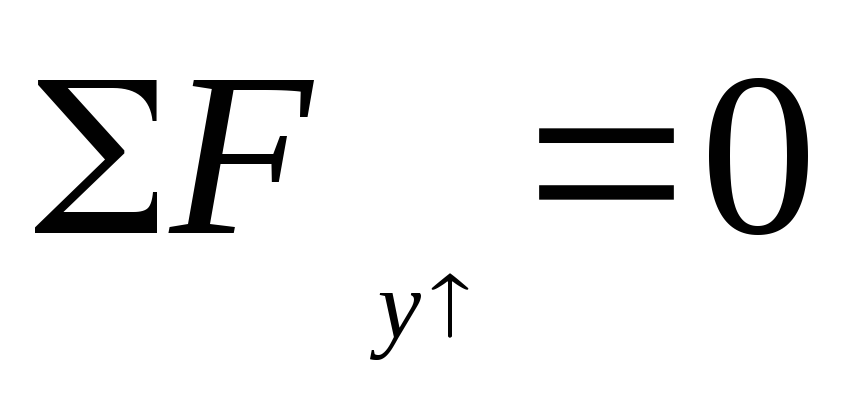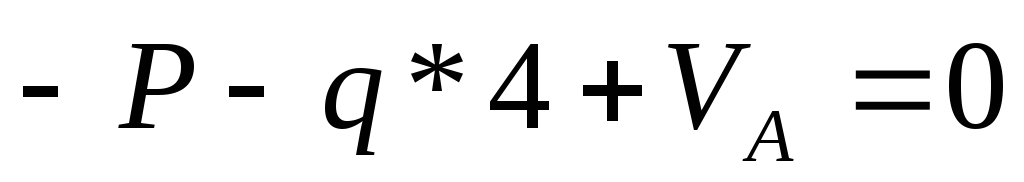
2. N=?

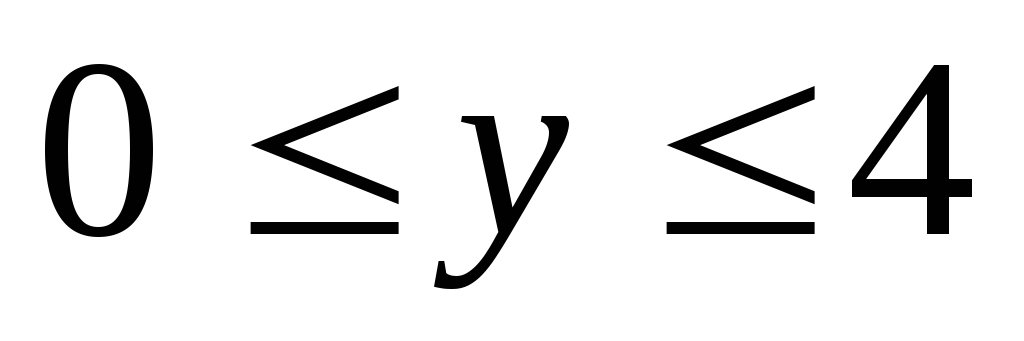
РОЗУ

:

N(0)= -P=-50 кН

N(4)= -50-40= -90 кН

СНиП: сталь:

К=1,2.. – коэффициент запаса прочности

Расчетное сопротивление для конструкций стали:

, i – конкретная точка по длине стержня

(9) – формула расчета на площадь при растяжении и сжатии

А=const

Расчет ступенчатого стержня на растяжении и сжатии

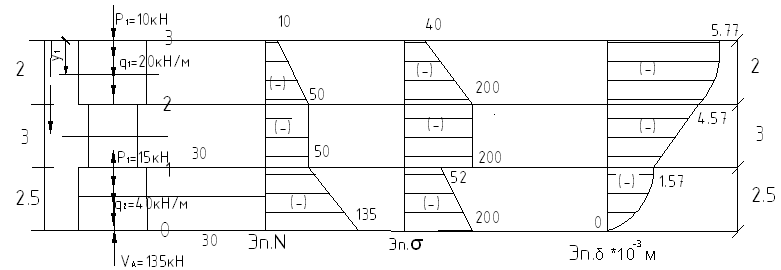
Модуль Юнга Е=2*10¹¹Па

1. Определение величины опорной реакции

V_A=?

2. Строим эпюру продольных усилий N

Эп.N=?

уч.2-3

РОЗУ

:

3. Уч.1-2

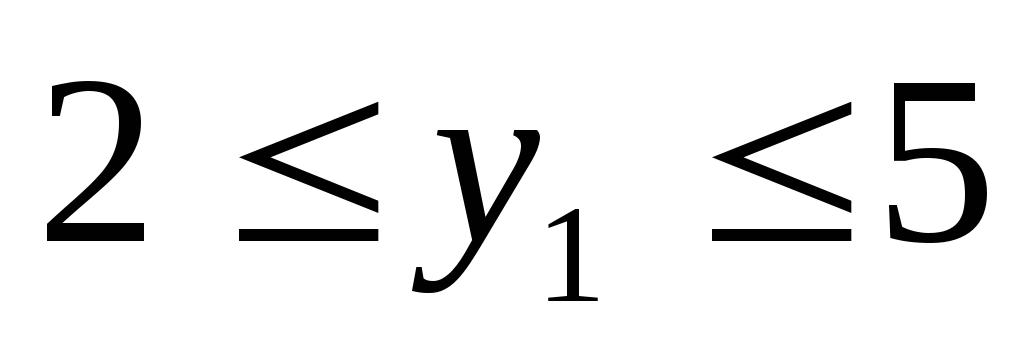
РОЗУ

:

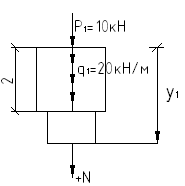
4. Уч.0-1

РОЗУ

:

На эпюре N всегда:

1. На участках без распределений нагрузки (где q_i=0) N_i=const

2. На участках с равномерно распределённой нагрузкой q_i=const, N_i=a_i+-q_i*y – прямая

3. Под каждой сосредоточенной силой на эпюре N реализует скачок на величине данной силы (P_j;V_k)

4. Подбираем площади A поперечных сечений стержня из условий их прочности

_{R- расчетное сопротивление}

5. 

6. _{Строим эпюру нормальных напряжений}

_{; i=1,2,3,…}

_{На каждом участке стержня необходимо рассмотреть 2 крайние точки}

_{Итак, эпюра всегда на каждом участке стержня подобна эпюре N.}

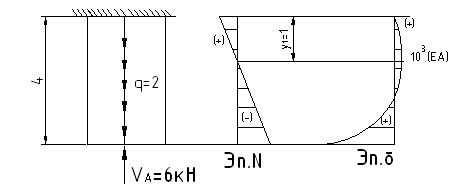
7. _{Строим эпюру вертикальных перемещений сечений бруса}

_{-при N=const – частный случай}

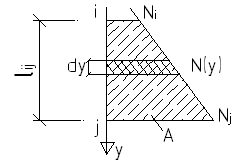
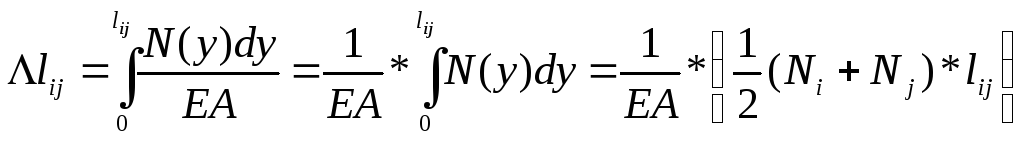
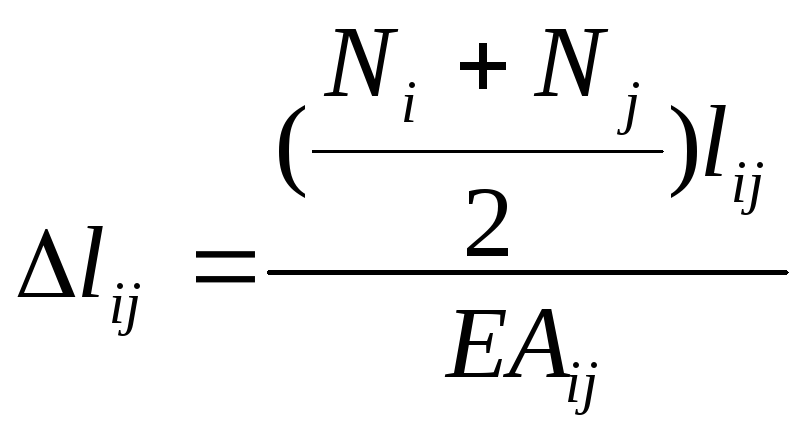_{(N – по закону прямых линий)}

_{(заделан. сечение)}

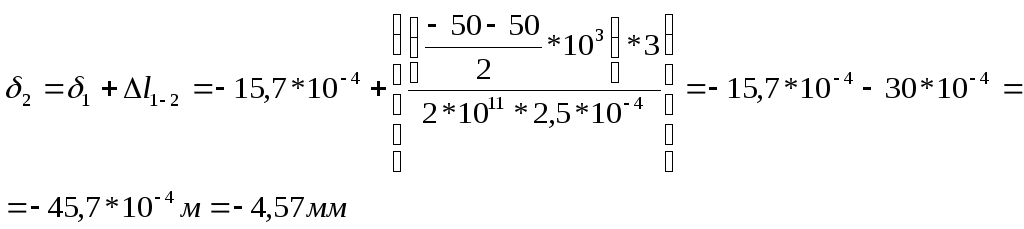
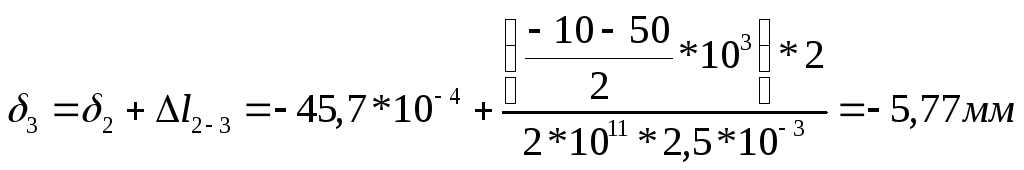
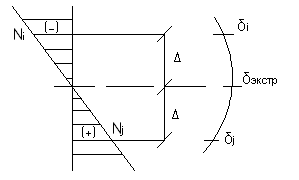
_{Рассмотрим отдельный случай, когда на участке стержня эп.N проходит через 0 график}

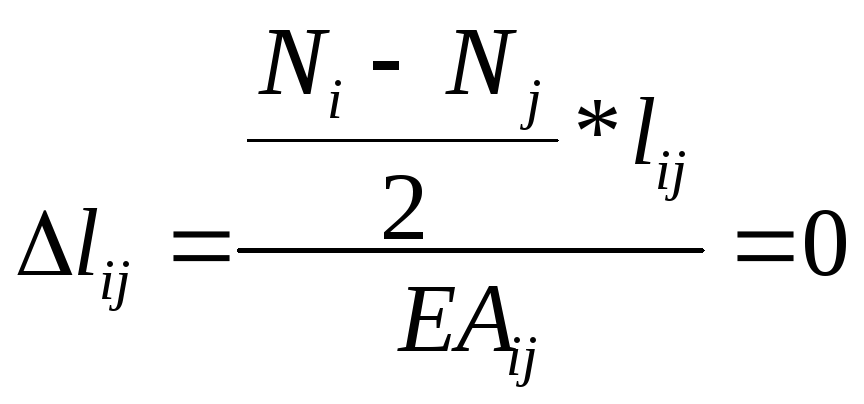
_{В сечении, где N=0}

_8-2x=6x

_8=8x

_x=1

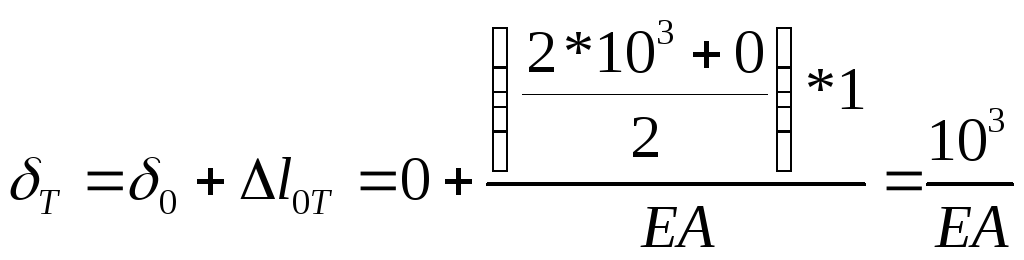
_{Итак, эп.} δ всегда:

1) на участке, где q_i=0 - прямая

2) на участке с распределённой нагрузкой, q_i=const

_{-парабола}

_{3) эп. непререрывна (на ней нет скачков)}

_{4) в заделанном сечении стержня}

_{5) в сечении, где N=0,}

Лекция 5

_{Статически определимые и статически неопределимые задачи при растяжении и сжатии}

_{В статически определимых задачах неизвестные находят из уравнений статики}

1. _{В статически неопределимых задачах уравнений статики недостаточно для нахождения неизвестных}

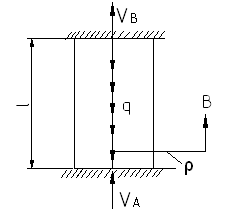
_{одно уравнение с 2-мя неизвестными}

₀₌₀

Необходимо записать 2-е уравнение из условия, что длина стержня L=const

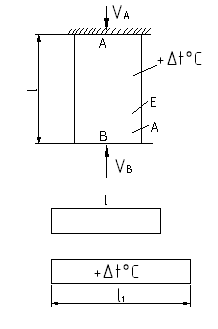
Рассмотрим температурную статически неопределимую задачу

При нагревании стержня он стремится расширится, однако этому препятствуют жесткие (несмещаемые) опоры

1. Статическая сторона задачи:

Составим уравнения равновесия

_{- одно уравнение с 2-мя неизвестными}

2. Геометрическая сторона задачи:

l=const, т.е. расстояние между т. А и В остается постоянным

Используем метод сечений (РОЗУ)

Разрежем стержень сечением непосредственно у нижней опоры B

Отбрасываем нижнюю часть конструкции, т.е. опору В

Заменяем отброшенную опору В реакцией V_B

Составляем уравнение

_{Которое соответствует отсутствию смещения т. В по вертикали:}

_,

₍₁₎

_{-коэффициент температурного расширения конкретного материала (1/град)}

_{Для меди}

_{Для стали}

_{Для бетона}

_{Возможность существования ж/б объясняется относительной близостью величин для стали и бетона}

_{Подставляя полученные слагаемые в выражение для и получаем}

_{Рассмотрим конкретные значения:}

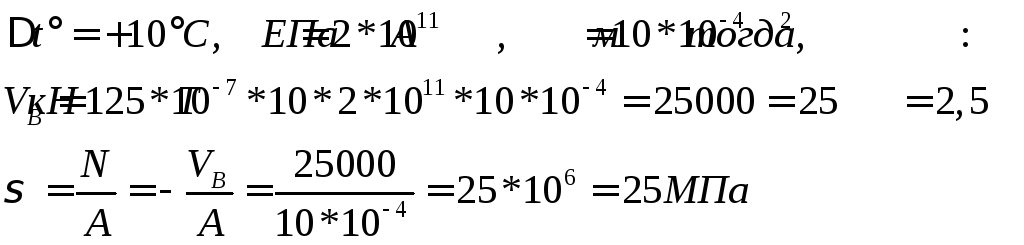
_{Итак, при решении задачи использовались:}

_{1.Ур-е равновесия}

_{2.Геометрические уравнения}

_{3.З-н Гука (физическая сторона задачи)}

_{Рассмотрим применение данного алгоритма к расчету следующей статически неопределимой системы:}

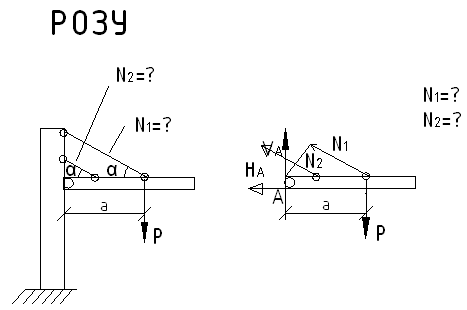
_{: одно уравнение с 2-мя неизвестными}

_{Для составления геометрического уравнения будем считать абсолютно жестким горизонтальный брус, который реально почти не изгибается при нагружении системы.}

_{Изображаем деформированное состояние системы}

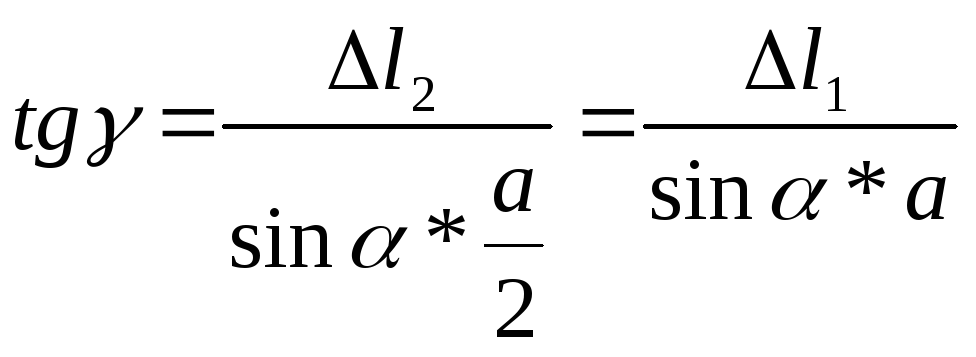_{(2) -геометрическое уравнение}

_{В геометрическое уравнение (2) не входят искомые усилия N1 и N2 , поэтому необходимо}

_{рассмотрение физической стороны задачи (уравнений закона Гука)}

₍₃₎

_А1=А2=А

_,

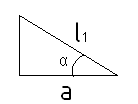
_{Подставляя данные формулы в уравнение (2)}

_{Рассмотрим пример статически неопределимой системы, когда усилие в одном из стержней является отрицательным}

_{Вновь считает брус абсолютно жестким.}

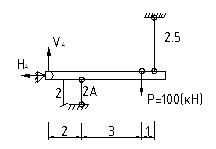
1. _{Уравнение статического равновесия}

_{: (1)}

₍₂₎

_{Данная запись необходима для того, чтобы в обоих частях равенства были положительные величины}

_{, (3)}