Лекция 27 вывод уравнения равновесия для элементарной части пластины

Сумма сил на вертикальную ось 0Z:

уравнения, полученные из составления моментов относительных осей x и y

Ур-ние Софи Жермен-Лагранжа -

основное дифференциальное уравнение изгиба пластинки, обычно записываемое в виде

Таким образом, расчёт любой пластинки сводится к решению ур-ния Софи Жермен при заданных граничных условиях (услов. закреп. её краёв).

ω – прогиб пластинки

– угол поворота

– изгибающ. мом.

– перерезыв. сила

H – крутящий момент

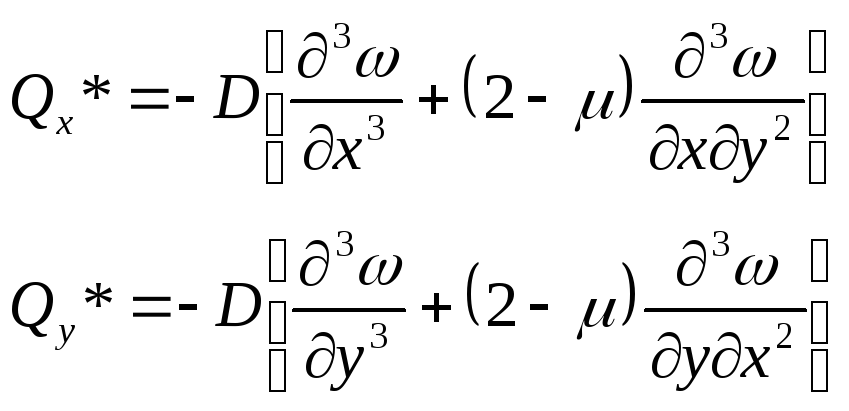- обобщенные поперечные силы Кирхгофа

Виды граничных условий

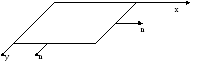
1. Край пластинки шарнир опёрт

2. Край пластинки жёстко защёмлён

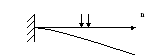
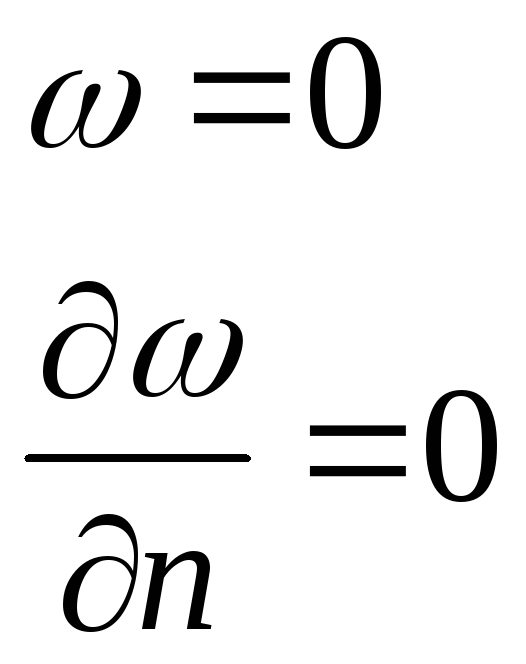
3. Край свободен от закрепления

Классификация граничных условий

Граничные условия бывают:

Геометрическими, статическими и смешанными.

– геометр. гр. усл.

– статич. гр. усл.

Граничные условия подразделяют на однородные и неоднородные .

Схема подхода к решению задач прочности пластины.

1. Анализ конструкции

2. Расчётная схема

3. Математическая модель

4. Численная реализация матем. модели

Построение аппроксимирующих функций статическим методом В.З.Власова

В.З.Власов (1906-1958гг) предложил способ построения функций распределения прогиба пластины, удовлетворяющих как граничным условиям, так и характеру распределения внешней нагрузки.

К входным параметрам относятся: a, b, h (м)-(1,2,3), толщина пластины; E(Па), μ(безр)- (4,5), условие закрепления (6,7,8,9); q(x,y) (10) (при расчете в размерном виде)

Σ10

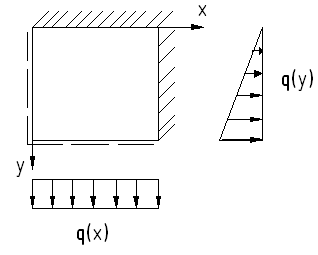
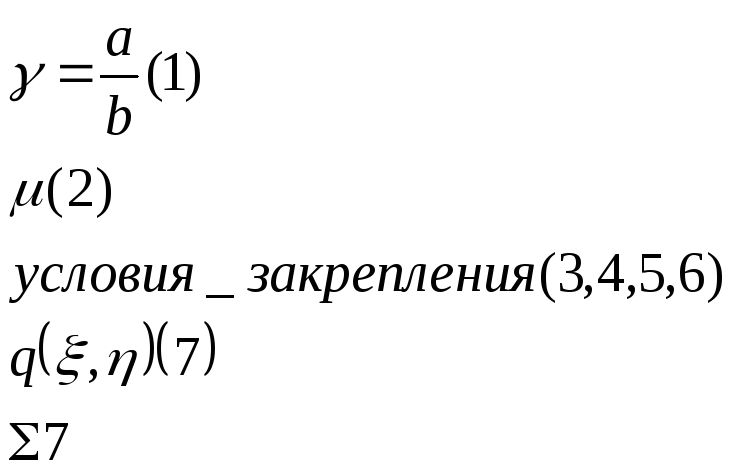
При решении в безразмерном виде решению соответствует бесконечное множество пластин для любых значений а(м), h(м), Е(Па)

Далее рассчитываем пластинку в безразмерном виде:

По алгоритму статического метода В.З.Власова необходимо:

1.Вырезаем из пластинки полоску по одному направлению

2.Рассматриваем данную полоску как обыкновенную балку

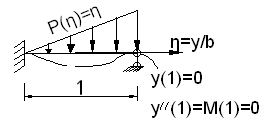
Дифференциальное уравнение изгиба балки имеет вид:

_{В безразмерном виде: (1)}

Кроме того используются граничные условия:

_;

Необходимо получить выражение y(η) и для ее производной.

Интегрируем выражение (1): _{; ;}

_{=> ; ;}

Используем граничные условия для нахождения С₁, С₂, С₃, С₄:

y(0)=0: 0+0+0+0+С₄ =0 => С₄=0

y^I(0)=0: 0+0+0+C₃=0 => C₃=0

Используем граничные условия на правом конце балки для подсчета величин С₁ и С₂:

_;

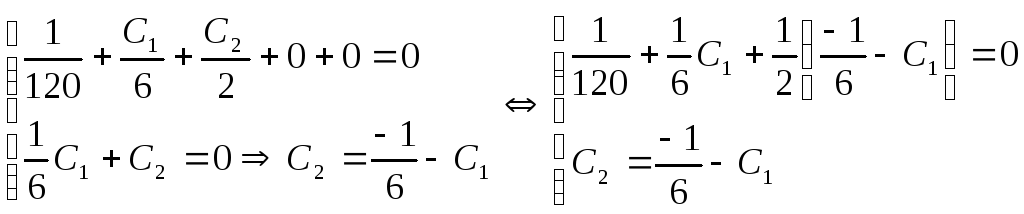
Подставляя полученные значения:

- точное решение для балки, но приближенное решение для пластинки, по направлению у.

Амплитуда прогиба пластинки не связана с амплитудой прогиба балки и затем будет найдена из решения задачи по одному из методов

В проведенный характер изменения прогиба пластинки по направлению оси η.

Т.е. для дальнейших расчетов применим:

Лекция 28

Построение аппроксимирующих функций статическим методом В.З.Власова

Аналогично поступаем по другому направлению:

Записываем дифференциальное уравнение изгиба балки, вырезанной из пластинки:

(1)

Граничные условия: х(0)=0, х^II(0)=0

Получаем выражение для х(ζ):

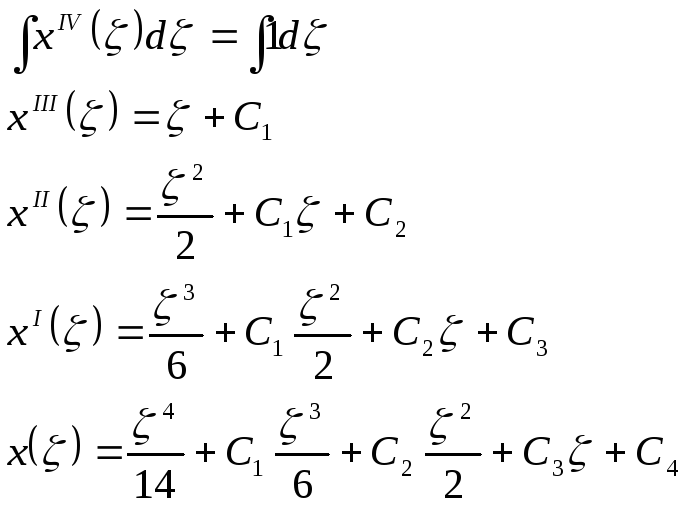
Используем граничные условия для нахождения произвольных постоянных интегрирования:

Принимаем для дальнейших расчетов:

Проверяем, удовлетворяет ли функция граничным условиям:

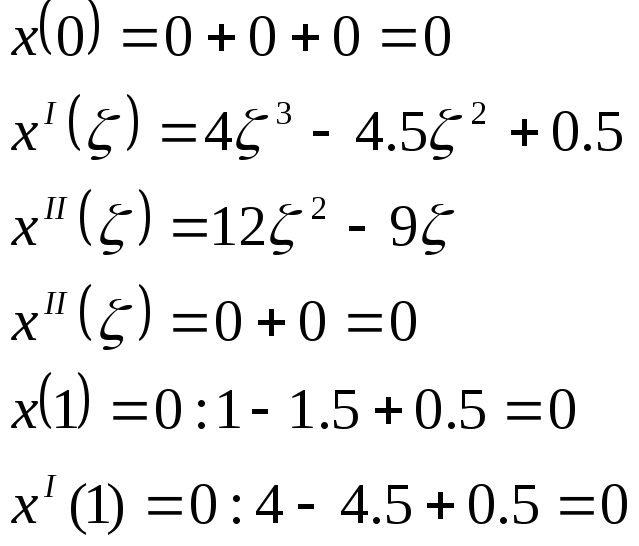
Таким же образом можно проверить функцию у(η):

Надо помнить, что старшая степень х(ζ)=4, т.к. нагрузка ζ и η поставлена. В у(η) старшая степень 5, т.к. нагрузка изменяется линейно.

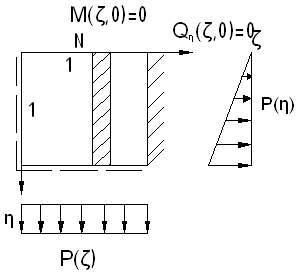
Рассмотрим пластинку со свободным закреплением края:

Вырезаем из пластинки полоску по направлению оси η. Рассматриваем балку.

Записываем дифференциальное уравнение изгиба балки:

На свободном крае:

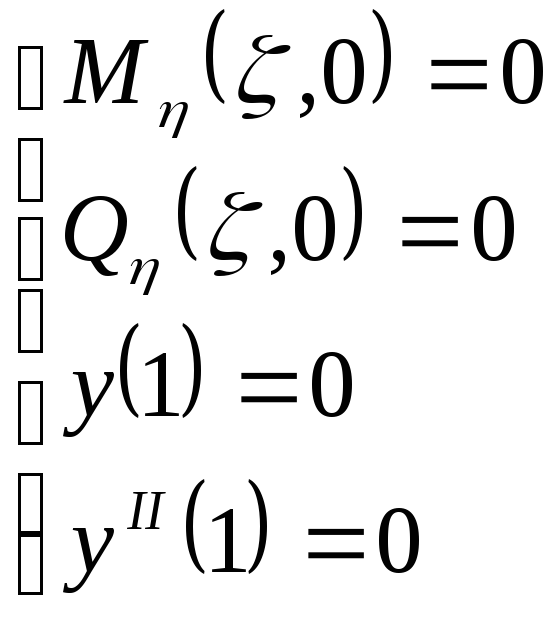
Рассмотрим выражение

и меняется вдоль свободной стороны, т.е. результат будет разный, если взять ζ=ζ₁, ζ=ζ₂, ….

Записываем функцию прогиба в виде: - запись с разделяющимися переменными, при этом в решении выносится некоторая погрешность.

Производим смягчение граничащих условий по принципу Сен Венона:

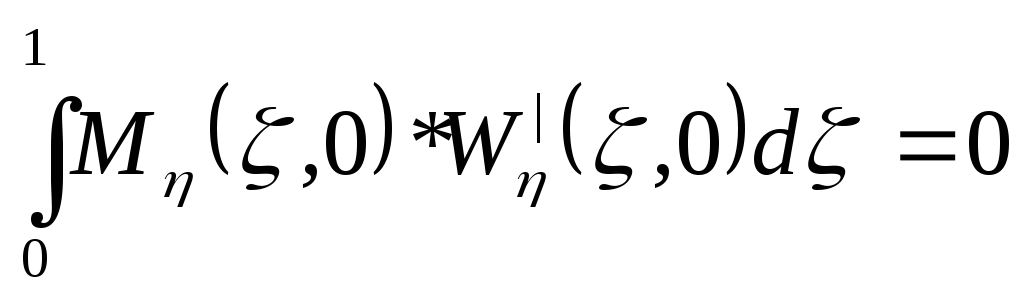- сумма работ изгибающих моментов на углах поворота вдоль стороны η равно 0. Данная запись следует из вариационной формулировки задачи.

Очевидно, что запись примет вид:

Интегрирование идет по ζ, поэтому величины, зависящие от η можно вынести за знак интеграла:

В данном случае у нас X(ζ)- известная функция: , поэтому величины определенных интегралов могут быть подсчитаны:

Известно, что

В EXCEL подсчет определенных интегралов:

В результате в полученной нами записи оказывается: обозначим

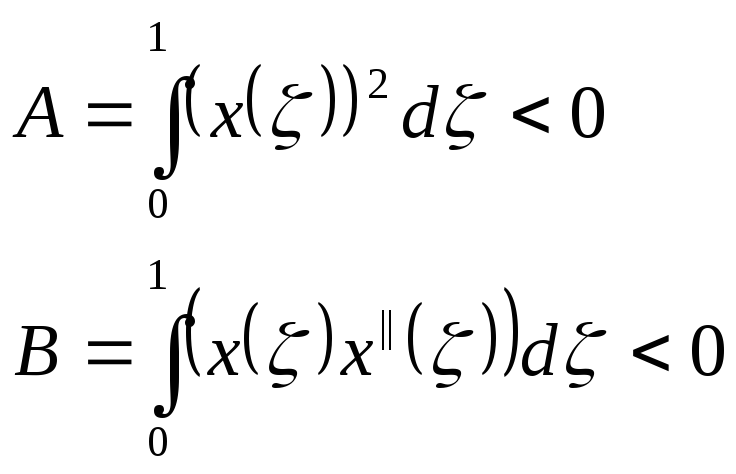
В результате получаем уравнения:

Подставляя сюда выражения для и:

(1)

Аналогично поступаем со вторым граничным условием:

- сумма поперечных сил Кирхгофа на прогибы 0

В результате некоторых преобразований получаем:

(2)

Дописываем (3) и (4) уравнения в данную систему:

(3)

(4)

Получаем систему четырех уравнений с четырьмя неизвестными.

На главной диагонали должны стоять не нулевые коэффициенты: