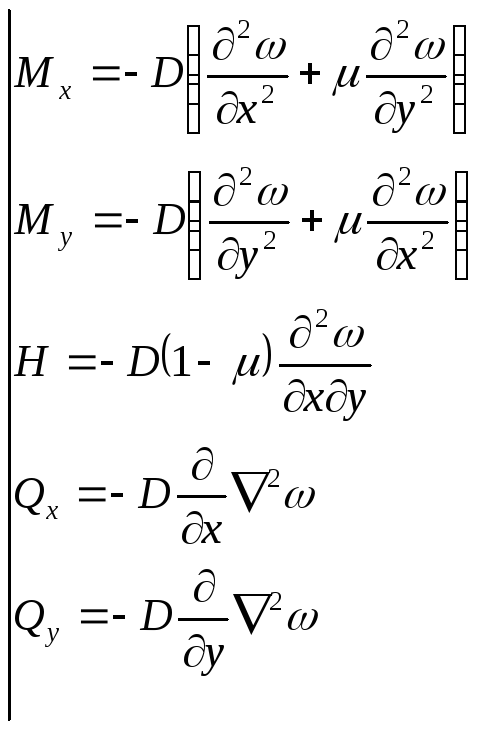- •Классификация объектов мдтт:
- •Гипотезы сопротивления материалов.
- •Принцип относительной жёсткости.
- •Лекция 2
- •Лекция 3 Расчет ступенчатого бруса
- •Лекция 4
- •Лекция 5
- •Лекция 6
- •Лекция 7
- •Лекция 8
- •Лекция 9
- •Лекция 10
- •Лекция 11
- •Лекция 12
- •Лекция 13
- •Лекция 14
- •Лекция 15
- •Лекция 16 балки на упругом основании
- •Составление уравнения прогибов y (z), углов поворота φ (z), изгибающих моментов м(z) и поперечных сил q(z)
- •Лекция 17 определение начальных параметров y0, φ0, m0, q0 из условий закрепления балки по концам
- •Построение эпюр y (z), φ (z), m (z), q (z) и реактивных давлений r (z)
- •Лекция 18
- •Внецентренное сжатие стержней.
- •Лекция 19
- •Лекция 20
- •Лекция 21
- •Лекция 22
- •Лекция 23
- •Лекция 24 Продольно-поперечный изгиб
- •Лекция 25
- •Лекция 26 Техническая теория изгиба пластин
- •Классификация пластинок
- •Упрощающие гипотезы теории пластин средней толщины
- •Лекция 27 вывод уравнения равновесия для элементарной части пластины
- •Виды граничных условий
- •Лекция 28
- •Лекция 29
- •Лекция 30
- •Лекция 31
- •Лекция 32
- •Лекция 33
- •Лекция 34
- •Явление усталости
- •Явление ползучести. Длительная прочность
- •Презентации
- •Учебные пособия
- •Видео-материалы
- •Список рекомендуемой иностранной литературы
- •2.2 Методические указания по проведению лабораторных работ
- •2.3. Методические указания по выполнению кр/кп
- •2.4. Методические указания по организации самостоятельной работы студента (срс)
- •2.5. Методические указания по выполнению ргр
- •Методические указания по курсу сопротивления
- •Тесты (прилагаются отдельным файлом)
- •Контрольные вопросы
- •Папка 4. Информационные материалы по дисциплине Выписка из Государственного образовательного стандарта
- •До изучения курса «Сопротивление материалов» студент должен изучить курс Высшей математики и курс Теоретической механики.
- •Министерство образования и науки Российской Федерации
- •3.Распределение трудоемкости (час) дисциплины по темам и видам занятий.
- •4.Содержание лекционного курса.
- •5. Перечень практических занятий
- •6. Перечень лабораторных работ.
- •7.Занятия для самостоятельной работы студентов.
- •8. Курсовой проект.
- •Экзаменационные вопросы.
- •13.Список основной и дополнительной литературы по дисциплине.
- •13.1 Основная литература.
- •13.2.Дополнительная литература
- •14.Использование наглядных пособий, тсо, вычислительной техники.
- •15.Дополнения и изменения в рабочей программе Рабочая программа пересмотрена на заседании кафедры
Лекция 25
Динамические воздействии. Удар падающим грузом.
К динамическим воздействиям относятся:
1.Колебания системы (система выводится из состояния равновесия и затем совершает колебания вокруг состояния равновесия)
2.Ударное воздействие (удар падающим грузом, внезапное полное нагружение)
3.Сейсмические воздействия.
Удар падающим грузом
Теория упругого удара заключает в себя следующее:
1)при ударе считается, что возникают только упругие деформации
2)кинетическая энергия падающего груза полностью переходит в энергию деформации системы (ударяемой)
3)не происходит рассеяние энергии на нагревание, на преодоление сопротивления среды.
В результате получается величина коэффициента динамичности:
![]() (1)
(1)
h -высота падения груза
![]() -
величина перемещения груза при его
статическом действии
-
величина перемещения груза при его
статическом действии
Существует следующий подход к решению задач:

![]() -
работа статически приложенной силы
-
работа статически приложенной силы
 -
пример груза, роняемого с высоты О
-
пример груза, роняемого с высоты О
Во всех остальных случаях необходимо знать высоту падения груза и прогиб при статическом действии груза.
Пример 1.
Продольный удар.

а) рассмотрим статическое действие груза

![]()
![]()
б) вычитаем напряжение при статическом действии нагрузкой:
![]() -
малая величина
-
малая величина
в)
предположим, что
![]()
![]() -
величина, сопоставимая с расчетным
сопротивлением данного материала.
-
величина, сопоставимая с расчетным
сопротивлением данного материала.
Рассмотрим аналогичную задачу для железобетонного стержня.
![]()
для бетона Е=3*1010 Па
![]() Па
Па
![]()
![]() (МПа)-
практически равно сопротивлению бетона
на сжатие.
(МПа)-
практически равно сопротивлению бетона
на сжатие.
Rсж=30 МПа
Rраст=1 МПа
Рассмотрим пример на поперечный удар.
На балку падает с высоты h груз Q

![]() (м)
(м)
Q=1000(H)=0.1(т)
h=0.02 (м)
![]() (Нм)
(Нм)
Тогда
![]() (см3)
=>
(см3)
=>
Возьмем
![]() №10:
№10:![]() (см3),
(см3),
![]() (см4)
(см4)
Определяем прогиб под грузом при его статическом действии

Определяем по формуле Симпсона:
![]()
Единым образом описать эпюру, представляющую собой ломанные линии, нельзя.
![]() (мм)
(мм)
Подсчитаем
величину динамического коэффициента:
![]()
Тогда
![]() (МПа)-
составляет больше половины расчетного
сопротивления.
(МПа)-
составляет больше половины расчетного
сопротивления.
Выясним, с какой высоты h можно ронять на данную балку данный груз.
![]()
![]()
Подбором определяем возможную высоту падения груза.
Учет деформированных опорных устройств при ударе
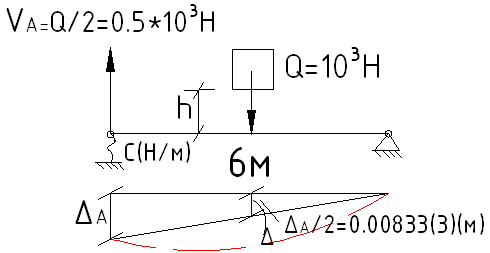
![]() см
см
На
величине
![]() под грузом накладывается величина
прогиба от статического действия груза,
т.е. 0,01136(м)
под грузом накладывается величина
прогиба от статического действия груза,
т.е. 0,01136(м)
Тогда
![]() (м)
(м)
 -
динамический коэффициент понизился,
по сравнению со случаем жесткой опоры
-
динамический коэффициент понизился,
по сравнению со случаем жесткой опоры
Динамические напряжения также понижаются:
![]()
Лекция 26 Техническая теория изгиба пластин
Пластикой будем называться тела, призматической или цилиндрической формы у которых один размер (толщина) мал по сравнению с другими размерами.

Классификация пластинок
В зависимости от вида напряженного состояния пластинки классифицируется так:
1.
Очень тонкие пластинки – мембраны, в
ней возникают осевые усилия N,
а изгиб. моментов нет M=0;Q=0.







2. пластинки средней толщины – плиты
![]() h
– толщина
h
– толщина
a – размер в плане
3.толстые плиты
![]()
4.гибкие пластины, промежуточный случай между 1 и 2
![]()

широко применяется в машиностроении
Упрощающие гипотезы теории пластин средней толщины
Гипотеза: При изгибе пластинки её толщина не меняется
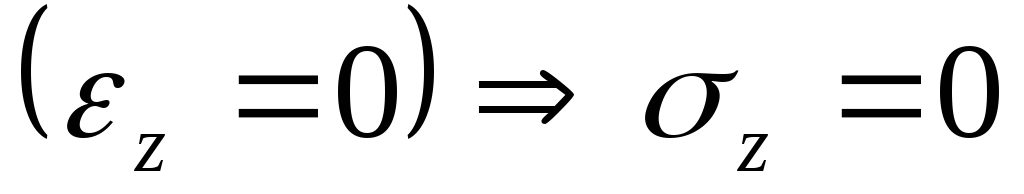 ,а плоскости, параллельные серединной
плоскости, друг на друга не давят.
,а плоскости, параллельные серединной
плоскости, друг на друга не давят.Гипотеза Кирхгофа о прямолинейном нормальном элементе
Всякое плоское до деформации вертикальное сечение пластины остаётся плоским и после деформации.

Гипотеза: При изгибе пластинки отсутствуют тангенциальные перемещения в её срединной плоскости при z=0, u=v=0
Следствия из введённых гипотез:
1. ![]()
2. 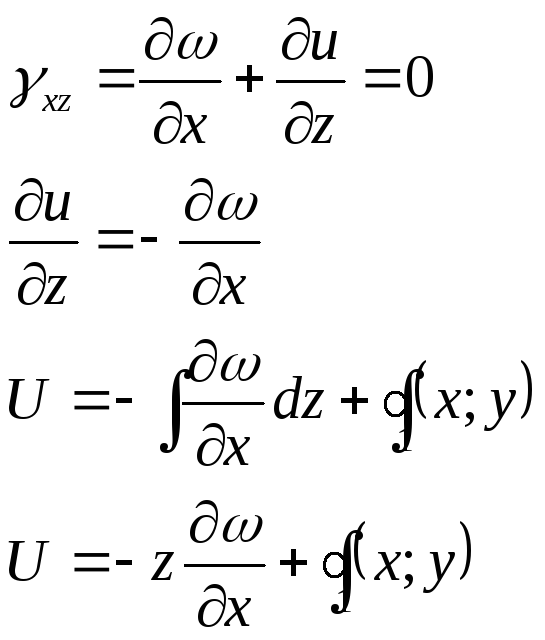

Используя
3 гипотезу, получим
![]()
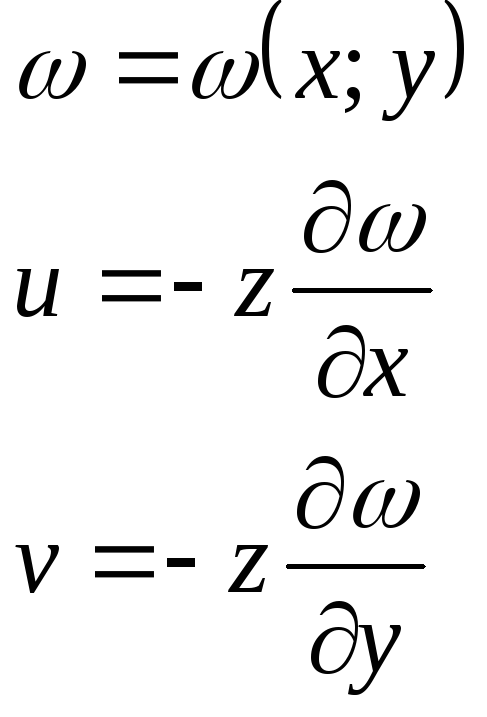 Таким
образом после введения 3-х упрощающих
гипотез, мы видим, что вместо 3-х неизвестных
функцийU,V,W
осталась одна неизвестная функция –
прогиб пластинки, которая не содержит
переменной z.
Таким
образом после введения 3-х упрощающих
гипотез, мы видим, что вместо 3-х неизвестных
функцийU,V,W
осталась одна неизвестная функция –
прогиб пластинки, которая не содержит
переменной z.
Будем рассматривать срединную плоскость.
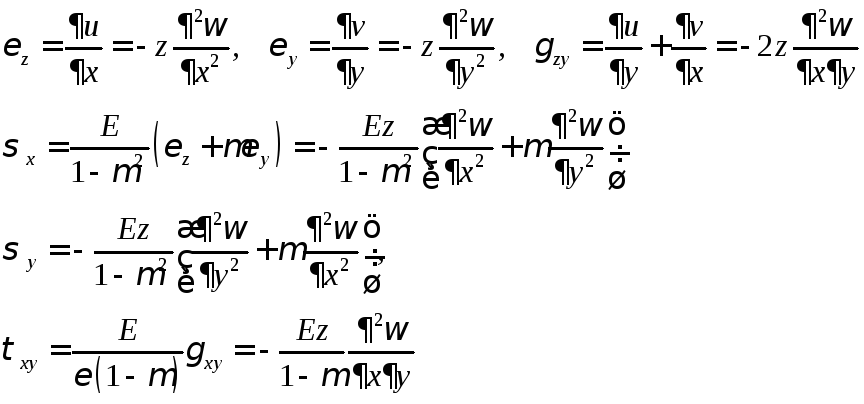
ВЫВОД ФОРМУЛ ДЛЯ ИЗГИБАЮЩИХ И КРУТЯЩЕГО МОМЕНТОВ И ПОПЕРЕЧНЫХ СИЛ

![]()
![]() – элементарный момент
– элементарный момент
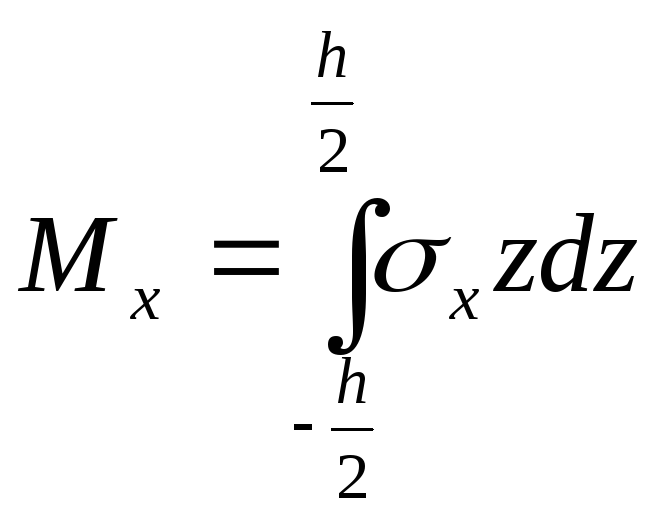 –изгибающий
момент
–изгибающий
момент
 ,EJ
– жёсткость при изгибе балки
,EJ
– жёсткость при изгибе балки
![]()

![]() –цилиндрическая
жёсткость изгиба пластинки
–цилиндрическая
жёсткость изгиба пластинки
![]()

R
– равнодействующая
![]() .
.![]()
H – крутящий момент
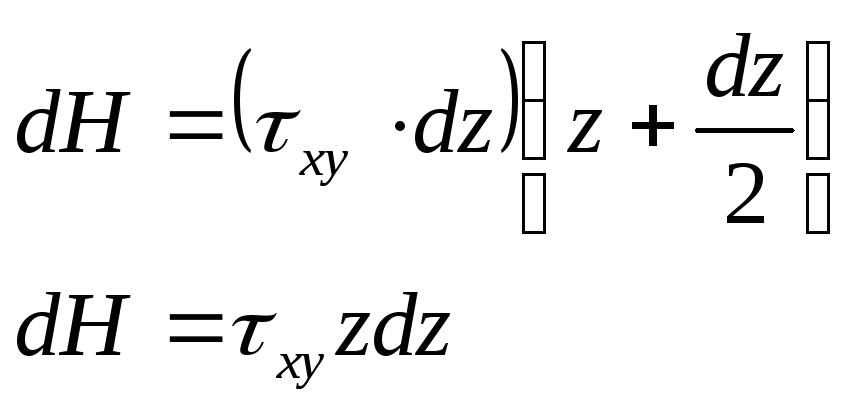

![]()