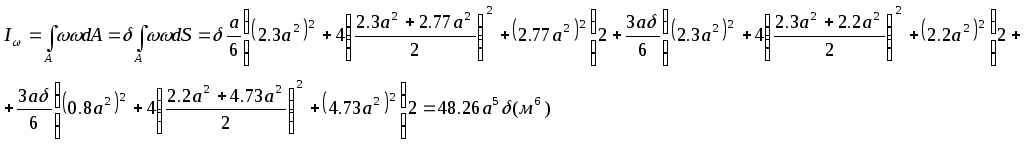Лекция 21

Тонкостенные стержни открытого профиля.

Рассмотрим некое тонкостенное поперечное сечение

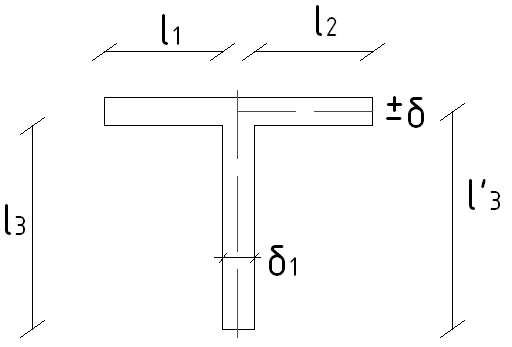
Считаем, что к тонкостенным профилям относятся такие, у которых:

(i=1,2,…,n)

Например у №10

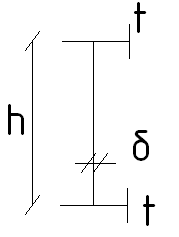
- толщина стенки

- высоко

У №40: d=0.8см; h-2t=40-2*1.35=37.3см;

Существуют более сложные тонкостенные поперечные сечения

Рассмотрим особенности работы тонкостенных поперечных сечений:

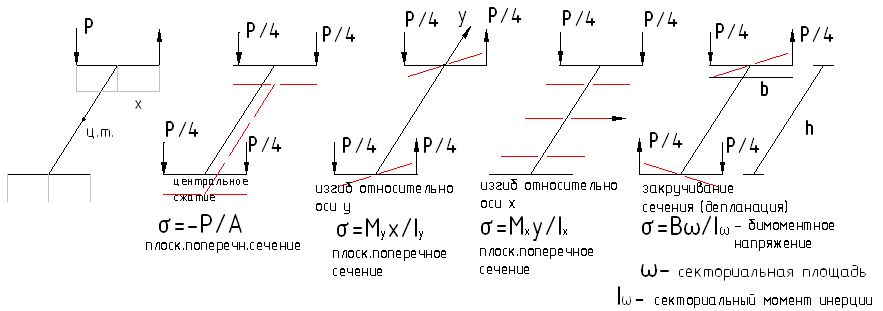
По (рис.1): (Нм²)

Рассмотрим задачу на внецентренное сжатие двутаврового поперечного сечения.

Возьмем №12:h=12см, b=6.4см, d=0.48см, t=0.73см, А=14.7см², ,,,

Выясним максимальную величину допускаемой силы при приложении ее к точке А₁, А₂, А₃.

;

;

;

Поделим Р_доп при расположении сжимающей силы в точке А3

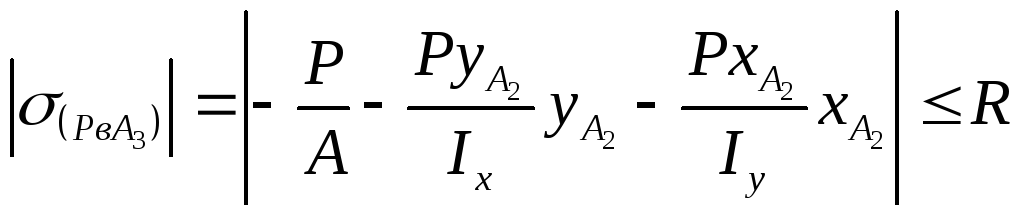
или:

;

Эксцентриситет сжимающей силы относительно оси у вызывает резкое снижение величины допустимой нагрузки для двутаврового поперечного сечения.

Попытаемся подсчитать координаты пересечения нулевых линий с осями X и Y.

- нулевая линия

На оси х: ;

На оси у: ;

Выясняем, какова будет эпюра напряжений в сечении сжатой двутавровой стойки.

Полный расчет сжатой стойки предполагает полное исследование ее устойчивости:

считаем, что потеря устойчивости может произойти в плоскости наибольшей жесткости.

; ;;

Подсчитаем гибкость:

Очевидно, что величину критической силы можно определить по формуле Лосинского:

Данная величина меньше, чем Р_доппри простом сжатии без возможности потери устойчивости.

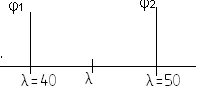
Допускаемое напряжение подсчитывается по формуле:

Лекция 22

Расчет изгибаемых балок с тонкостенным поперечным сечением

Тонкостенностью называются поперечные сечения, у которых

а- длина элемента профиля

δ- толщина элемента профиля

Для тонкостенных поперечных сечений дополнительно возникает напряжение:

(1)

Причем вносит существенный вклад в общее напряженное состояние.

Сначала необходимо определить все геометрические характеристики поперечных сечений

1. Определение положения центральной точки поперечного сечения:

выбираем произвольную ось OY

Координаты центральной точки определить по формуле:

Подсчитаем статические моменты площади и площади поперечного сечения:

- при этом все размеры берутся в осях элемента.

- решение между осью у и центральной точкой сечения.

2. Определяем величины Моментов инерции сечения относительно оси X_c и Y_c

по формуле Симпсона.

Можно построить эпюру у:

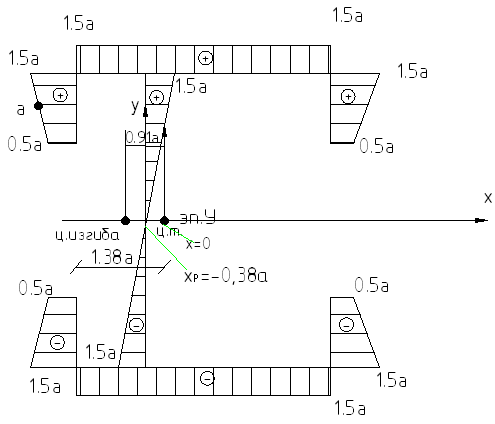
- формула Симпсона

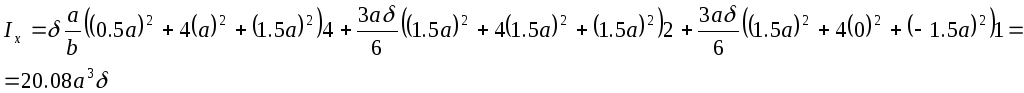
Аналогично может быть подсчитана величина Iy:

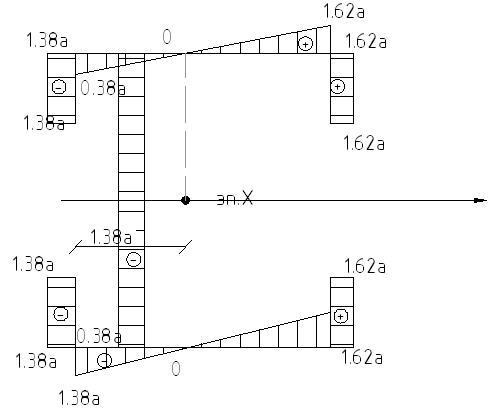
Если использовать для подсчета геометрических характеристик точное выражение, то получаем:

. Погрешность в вычислениях:

Статический момент площади:

Координаты центра точек:

, погрешность

,

Итак, выполненные приближенные вычисления обладают высокой точностью.

В формуле для моментных напряжений:

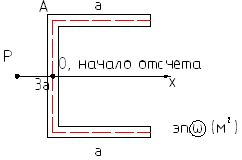
Определение: секториальной площадью называется величина, равная удвоенной площади треугольников, описывающих при движении точки по оси элементы сечения.

Правило №1: в местах соединения элементов профиля

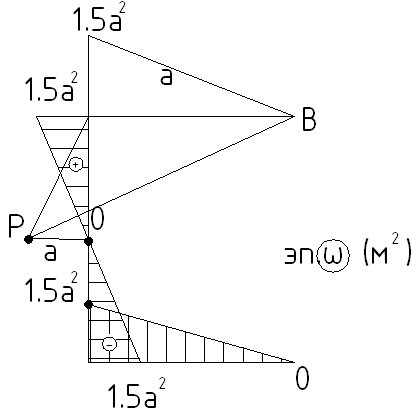
Правило №2: при движении конца вектора по прямой, меняется по закону прямой линии.

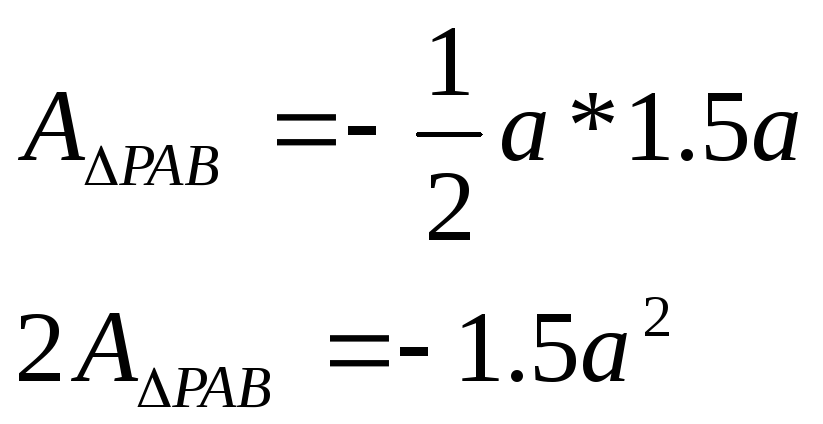
При определенном выборе положения полюс эпюра получается в простейшем полюсе.

Правило №3: если при движении вектора по прямой треугольники получается вырожденными, то площадь

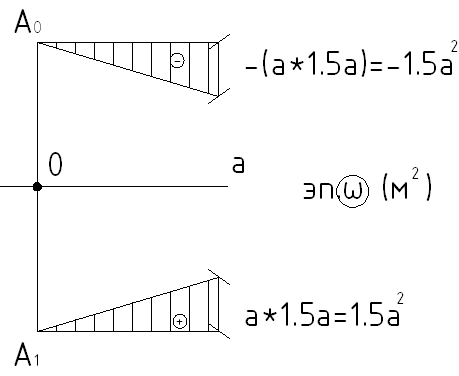
Для дальнейших вычислений стремимся к наибольшей простой эпюре .

Понятие о центре изгиба:

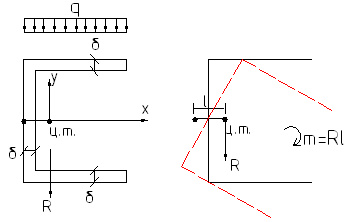
Если равнодействующая, приложенная к нагрузке R, проходящая через центр точки сечения, то создается момент, равный произведению R на решение между центром точки и центром изгиба.

В результате поперечное сечение будет закручиваться вокруг центра изгиба, в данном случае по часовой стрелке.

Если равнодействующая R действующая в точке изгиба, то сечение деформируется без закручивания и напряжение можно подсчитать по формуле:

В реальном случае: , причем второе слагаемое вносит существенный вклад в напряженное состояние.

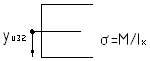
Для получения центра изгиба используется формула:

(2)

- центробежный секториальный момент относительно оси Х.

Тогда

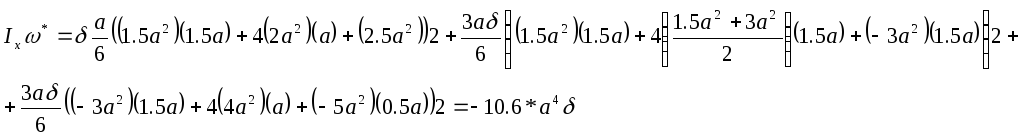
Тогда координата центра изгиба получается по формуле:

: в главных центральных осях (I_ц) необходимо отстроить по оси ОХ на 0,91.

Для дальнейших вычислений потребуется эпюра , взятая для полюса в центре изгиба:

В формулу напряжения входит секториальная величина для ω: