Лекция 20

Устойчивость стержней

Устойчивость- способность объекта сохранять исходное состояние в равновесии и проектной форме деформирования при действии расчетных нагрузок.

Примеры потери устойчивости:

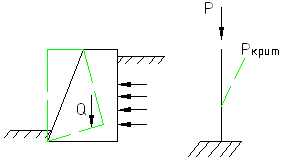
Изогнутое состояние- потеря устойчивости.

41% аварий происходит за счет потери устойчивости элементов конструкции.

Теоретически устойчивость стержней исследовал Л. Эйлер (18в.).

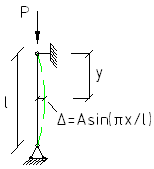
Формула Эйлера: (1)

Р_крит- номинальная критическая сила, при которой происходит потеря устойчивости стержня.

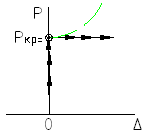
Формула (1) соответствует шарнирному закреплению стержня по концам.

,

На практике условие закрепления стержней весьма разнообразное. Поэтому необходимо рассматривать всевозможные варианты.

Вводим понятие о приведении длины стержня:

- безразмерный коэффициент приведения длины

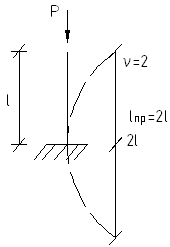
Полуволна синуса набирается на длине

При этом формула Эйлера имеет вид:

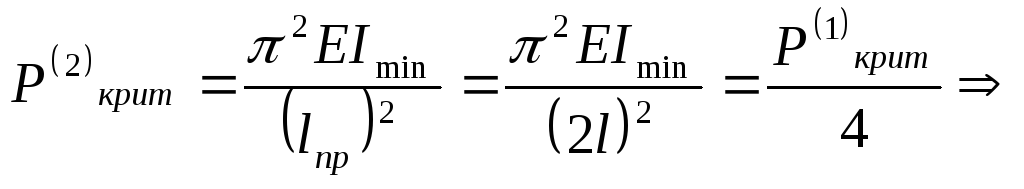величины критической силы в 4 раза меньше по отношению к случаю (1).

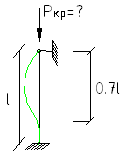
с увеличением жесткости опорных устройств величины критических сил возрастают.

- длина реализации полуволны синуса.

Рассмотрим самый жесткий, возможный вариант закрепления:

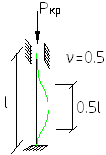
наивысшее возможное значение критической силы при закреплении стержня по концам.

наличие горизонтальных опорных стержней по длине стержня существенно увеличивают величины Р_кр.

Рассмотрим, что происходит в случае (4), если убрать одну из связей: (горизонтальная подвижность)

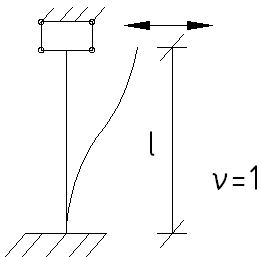
при удалении связи величина критической силы существенно понижается (устойчивость теряется при меньшем значении Ркр).

Обобщенная формула Эйлера:

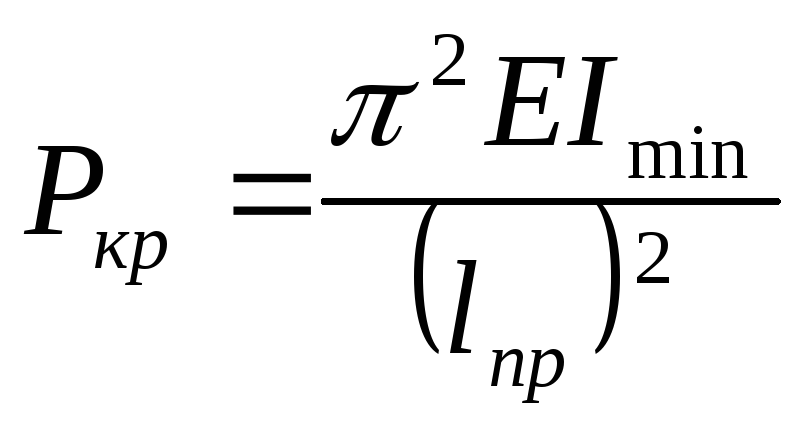
Справедливы следующие утверждения:

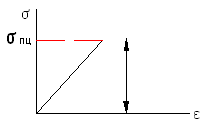
1. Потеря устойчивости происходит в пределах пропорциональной зависимости между напряжением и деформацией.

Формула (3) не применима

2. Сила действует строго центрально

3. Стержень является строго прямолинейным

4. Нет никаких поперечных воздействий на стержень

В реальности данное условие не выполняется

Рассмотрим случай, когда потеря устойчивости происходит при возникновении пластических деформаций:

1876-1888гг.- США- 251 катастрофа мостов.

Слепое следование формуле Эйлера (3)

Выясним, к чему ведет ограничение (1):

Переходя от критических сил к критическим напряжениям:

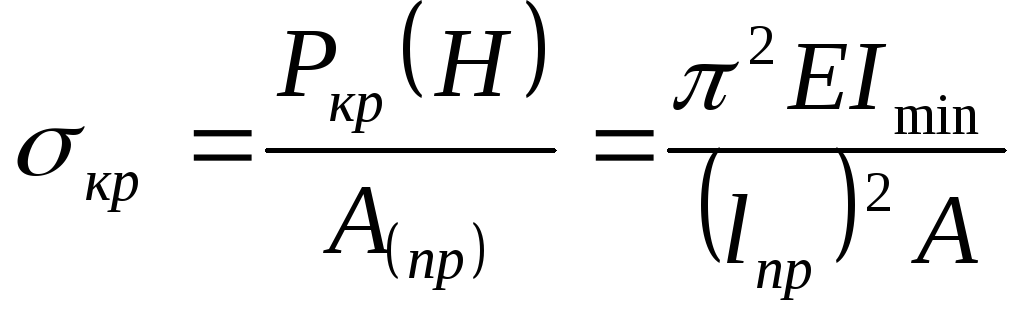
Во внецентренном сжатии введено понятие о радиусе инерции относительно оси:

(4)

Тогда:

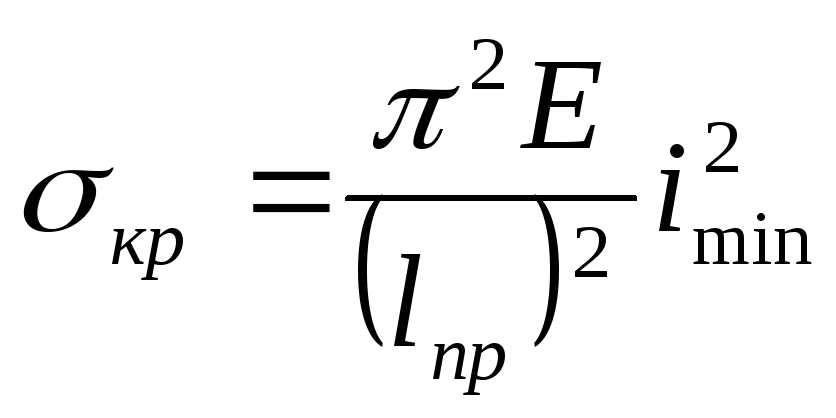
Вводим понятие о фундаментальной величине- гибкости стержня.

(5)

Например, если увеличивается длина стержня, то пропорционально увеличивается его гибкость.

При сокращении габаритов поперечного сечения стержня уменьшается .

Формула для тогда имеет вид:

Отсюда находим предельное значение гибкости λ:

(6)

Если , то можно использовать формулу Эйлера:

Для стали: ;;

Для сосны: ;;

Для бетона: ;

В результате проведения опытов под криволинейными центральносжатыми стержнями, получаются следующие критических напряжений:

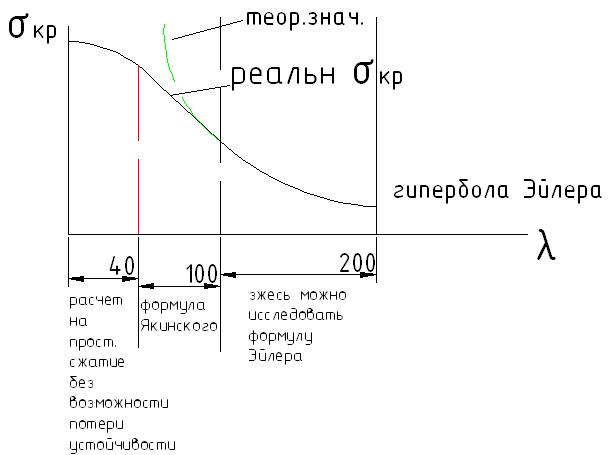
Формула для при возможности возникновения пластичной деформации перед потерей устойчивости.

Формула, полученная в результате обработки данных многочисленных опытных исследований, имеет вид:

(7)

a и b – экспериментальные коэффициенты (получены статической обработкой данных опытов)

Для стали: а=300(МПа); b=1.14(МПа)

При подстановке N получаем (линейная зависимость)

По Ясинскому:

Разделом между формулами является величина

- формула Эйлера

- формула Ясинского

Практический способ расчета стержней на устойчивость:

Величина Р_кр считается лишь для идеальных стержней:

а) идеальный стержень прямолинеен

б) центрально-сжатый

в) без внутренних полостей

г) без боковых воздействий

В реальности стержни теряют устойчивость при величинах

При этом величина ,- коэффициент запасоустойчивости

Общепринято вести расчет следующим образом:

Считаем, что

Тогда формула принимает следующий вид:

(8)

(9)

Для каждого материала составляем таблицу в соответствии между гибкостью и величиной

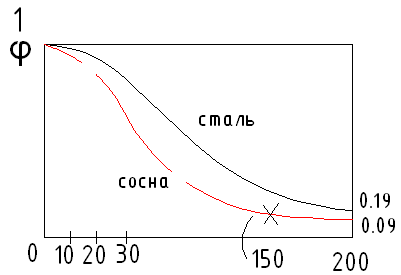
Рассмотрим алгоритм использования формулы (9). В нее входят две неизвестных величины А и . Обычно задают

Тогда

_,

Далее определяем гибкость стержня:

В табличные значения даются с шагом 10 по

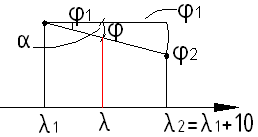
(10)

После этого сопоставим полученные величины с ранее взятыми величинами. Если они различаются существенно, то:

Возвращаемся на подсчет площади поперечного сечения с новым значением

Доказано, что данный процесс сходится к точному значению для конкретного числа шагов.

При наличии опыта проектирования конкретных стержней возможно назначать величины , исходя из конкретных прежних данных. После подсчета окончательных габаритов поперечных сечений вычисляем величину, которую необходимо округлить до разумной величины. Кроме того, известна величина:

да:

нет:

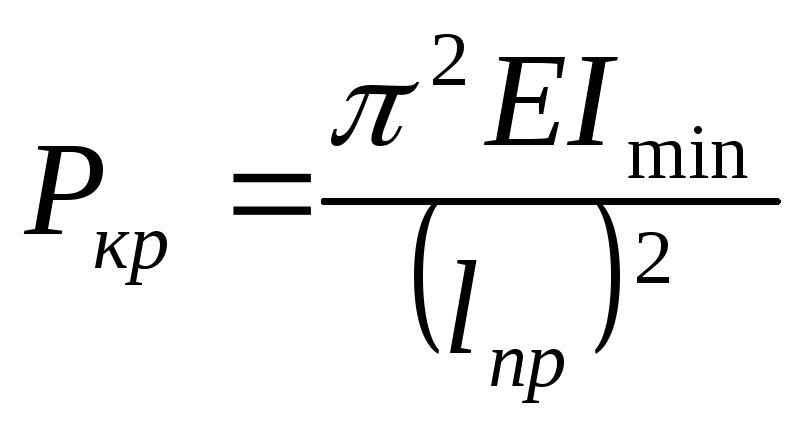
из них следует:

Для стальных конструкций