Лекция 19

_{Косой изгиб}

Он встречается во многих элементах строительных конструкций.

α- угол между линией действия силы и главной осью балки.

Общим является то, что балка изгибается в плоскости, не совпадающей ни с одной из главных осей. Изобразим силу, действующую под углом к главным осям балки.

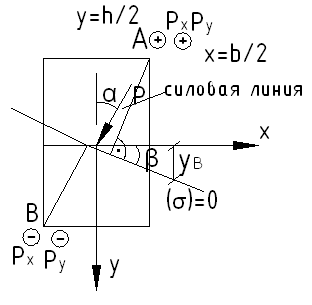
_{Рис. 1}

_{Аналогичная ситуация возникает при торможении груза.}

_{Ранее изучался изгиб относительно главных осей. Раскладываем силу Р на две составляющие}

_{Ру вызывает изгибание балки относительно оси х:}

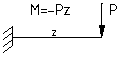Рис.2

_{Аналогично записывается выражение для другой составляющей силы Рх}

_{Суммарное напряжение в точке поперечного сечения:}

₍₁₎

_{- характер изменения изгибающих моментов вдоль оси z.}

_{Знаки в формуле (1) зависят от выбранного напряжения осей х и у.}

_{Очевидно, что в формуле (1) для балки с (рис.2) с нагрузкой с (рис.1) напряжение будет следующим:}

_{; ,}

_{Необходимо найти точки сечения, в которых действует наибольшее нормальное напряжение.}

_{После этого с использованием условий прочности необходимо подобрать габариты поперечного сечения, а затем определить наибольшие возможные действующие нагрузки, после чего необходимо проверить величины напряжений, действующих в сечении}

_{Как и при внецентренном сжатии точки наиболее удалены от нейтральной линии, на которой}

Из условия _{получаем:}

_{β- угол между нейтральной линией (где ) и осью х.}

_{Можно записать выражение для}

₍₂₎

_{Если , то силовая линия перпендикулярна нулевой линии.}

_{Приведем сечения, для которых это выполняется безусловно}

Для этих геометрических фигур косой изгиб никогда не реализуется.

Косой изгиб реализуется лишь в тех балках, у которых _:

_{Например, он реализуется для прямоугольного поперечного сечения:}

_;

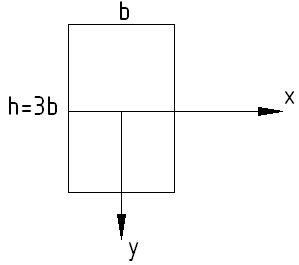
_{При этом}

_{Для доски (прямоугольной) 5х15см нулевая линия будет почти горизонтальной.}

_{Первый вариант существенно экономичней.}

Наибольшие напряжения возникнут в точках, отмеченных (+)(+) и (-)(-).

Определяем напряжения в данных точках:

_{При косом изгибе главной является проверка на растяжение, т.к., как правило, .}

_{Вышеприведенное относительно к расчету по первому предельному состоянию (по прочности).}

_{Переходим к расчету по второму предельному состоянию (по деформативности). Рассмотрим идеализированный случай прямого изгиба балки.}

Определяем прогиб на конце консольной балки.

Перемножим эпюры М и М₁ по формуле Симпсона.

_{Переходим к косому изгибу, тогда:}

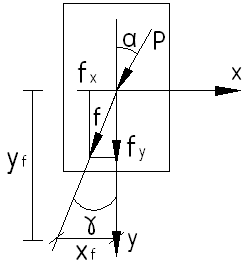
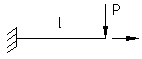Относительно оси у прогиб вызывается силой и составляет

По оси х перемещение вызывается силой _:

_{Результирующий вектор прогиба будет определяться по теореме Пифагора:}

Подсчитаем угол _{, составленный вектором прогиба у:}

_{Запишем: (3)}

Данная формула совпадает с формулой

_{Отсюда следует, что вектор прогиба перпендикулярен нулевой линии.}

_{Для балок различной назначения устанавливается свое собственное отношение , для балок на двух опорах эта величина = 1/450.}

_{Рассмотрим пример по косому изгибу.}

_{Зададим пролет двутавровой балки, нагрузку на нее:}

Зададим угол отклонения при торможении

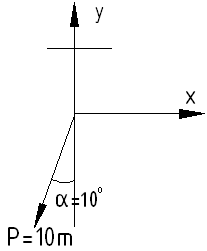
Очевидно, что:

_{Тогда ;}

_{Максимальное напряжение составляем:}

_{Сначала подбираем балку при прямом изгибе нос запасом прочность}

С запасом принимаем №55:

№55

Проверим данное сечение:

Из-за второй составляющей (горизонтальной) σ_max существенно превышает расчетное сопротивление.

Предположим, что возьмем наибольший №60:

Тогда:

Вывод: сечение необходимо делать из двух прокатных двутавров, так как двутавр №60 не удовлетворяет условию прочности.