Radzevich, S.P. Monograph - 2001

цилиндрические) вырождаются в полярные координаты.

3.7.3. Взаимосвязь между цилиндрическими и сферическими координатами. В текущей точки M на поверхности Д И ее цилиндрические и сферические координаты связаны следующими зависимостями:

и

M r M sin M ; M M ; Z M r M cos M .

3.8.О линейных преобразованиях

Кроме координатного и отображающего преобразований в практике обработки сложных поверхностей деталей на многокоординатных станках с ЧПУ находят применение и другие виды отображений. Если обрабатываемая деталь обладает симметрией (центральной, зеркальной или одновременно центральной и зеркальной), в памяти системы ЧПУ металлорежущим станком достаточно иметь данные, описывающие лишь часть обрабатываемой поверхности Д детали. В этом случае необходимая информация обо всей поверхности Д детали может быть получена при помощи вращений, сдвигов и отображений. Этим достигается более рациональное использование объема памяти системы ЧПУ металлорежущим станком. Выполняемые преобразования симметрии, сдвига, изменения масштаба по осям координат и т.п. являются преобразованиями объектов и не оказывают влияния на систему координат, в которой деталь описана. С такими преобразованеиями можно познакомиться по работам (Faux, I.D., Pratt, M.J., 1987; Marciniak, K, 1991; Mortenson, M.E., 1985). Матричное описание вращений вокруг координатной оси, вокруг оси, произвольным образом ориентированной в пространстве, в т.ч. как проходящей, так и не проходящей через начало координат, достаточно подробно описано в литературе (Люкшин В.С., 1968). Использование матриц для получения проекций геометрических образов на координатные плоскости рассмотрено в (Marciniak, K, 1991).

Гл а в а 4. Геометрия касания поверхности детали

иисходной инструментальной поверхности

Эффективность формообразования поверхностей деталей зависит от множества различных факторов. Для определения наивыгоднейшего значения каждого из факторов и наилучшего сочетания всех факторов вместе взятых требуется информация. Часть необходимой информации содержится в исходных данных – в чертеже детали: это сведения о форме и параметрах обрабатываемых поверхностей, требования к точности их обработки, взаимного расположения и пр. Другая часть информации, необходимая для решения задачи синтеза наивыгоднейшего формообразования поверхности детали, генерируется в процессе разработки технологии изготовления детали, в частности, при подготовке управляющих программ для системы ЧПУ металлорежущим станком. Эту часть информации можно рассматривать как промежуточную – в окончательно разработанном технологическом процессе в явном виде она отсутствует. Дополнительным источником, позволяющим генерировать вторую часть необходимой информации, служит геометрия касания поверхности детали и исходной инструментальной поверхности.

В соответствие с дифференциально-геометрическим методом (Радзевич С.П., 1991) решение задачи синтеза наивыгоднейшего формообразования поверхности детали основано на том, что поверхность Д

является первичной. Чтобы исходя из этого можно было решить задачу определения вида и параметров исходной инструментальной поверхности И наивыгоднейшего инструмента для обработки заданной поверхности детали, а затем синтезировать наивыгоднейшую кинематику формообразования, необходимо аналитически описать геометрию касания поверхности Д детали и ИИП И инструмента в каждый момент

формообразующей обработки.

Характер касания поверхностей Д и И , параметры их локальной топологии и относительная локальная

ориентация определяют эффективность применяемого способа обработки детали. Эффективным средством увеличения производительности и повышения точности формообразования поверхностей деталей гладким регулярным отсеком поверхности И инструмента является управление значениями параметров локальной топологии поверхностей Д и И в точке K их касания, которые определяют геометрию касания этих

поверхностей.

Используются различные аналитические методы описания геометрии касания поверхности детали и исходной инструментальной поверхности в дифференциальной окрестности точки их касания (Радзевич С.П.,

1987).

В процессе формообразования поверхность Д детали и поверхность И инструмента являются

сопряженными: в относительном движении в каждый момент времени они касаются одна другой и имеют не менее одной общей точки – точки K их касания. Если поверхности Д и И касаются одна другой в точке, то

точка К будет единственной (или их множество конечно, когда поверхности Д и И касаются одна другой

одновременно в нескольких точках – такие случаи в практике формообразующей обработки деталей встречаются как исключение). Если же поверхности Д и И касаются одна другой вдоль некоторой линии –

характеристики E , или в пределах некоторого участка поверхности Д , множество точек касания

бесконечно.

Понятие геометрия касания поверхности Д детали и поверхности И инструмента подразумевает как

качественную, так и количественную оценку соотношений элементов их локальной топологии в точке K и охватывает различные подходы к аналитическому описанию полноты прилегания поверхности И к поверхности Д . Для этого используются геометрические образы, обобщающие элементы локальной

топологии обеих поверхностей Д и И и представляющие собой своеобразный комбинированный геометрический образ.

Интуитивное представление о геометрии касания поверхностей Д и И и о полноте их прилегания одна к другой (т.е. о степени конформности1 исходной инструментальной поверхности И к обрабатываемой поверхности Д детали) можно получить из простого примера. Пусть выпуклая сфера некоторого радиуса

касается:

-другой выпуклой сферы;

-плоскости;

-вогнутой сферы некоторого (большего) радиуса.

Интуиция подсказывает, что в первом случае касающиеся поверхности наименее полно прилегают одна к другой, во втором – больше, а в третьем – еще больше. Степень конформности касающихся поверхностей в первом случае наименьшая, во втором – больше, а в третьем – еще больше.

Чтобы описать аналитически геометрию касания поверхностей Д и И требуется, чтобы обе эти

поверхности были аналитически представлены в некоторой общей системе координат и был образован замкнутый цикл прямого и обратного последовательного преобразования координат.

4.1.Образование замкнутого цикла последовательных преобразований координат

Под замкнутым циклом последовательных преобразований координат понимается такая последовательность их преобразований, при которой к любой из систем координат, входящих в цикл, можно прийти от любой другой системы координат, образующией этот цикл. В этом случае использование формулы (3.16) для всего цикла приведет к тому, что после выполнения всех входящих в цикл преобразований возвращаемся к исходной системе координат. Это необходимый и достаточный признак того, что цикл последовательных преобразований координат является замкнутым.

Введение в рассмотрение замкнутых циклов последовательных преобразований координат дает возможность рассматривать решение задачи синтеза наивыгоднейшего формообразования поверхности детали в любой из систем координат, образующих цикл, в первую очередь в той из них, в которой описание процесса наиболее удобно.

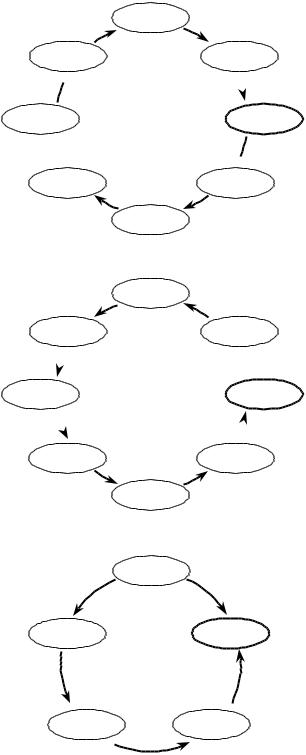
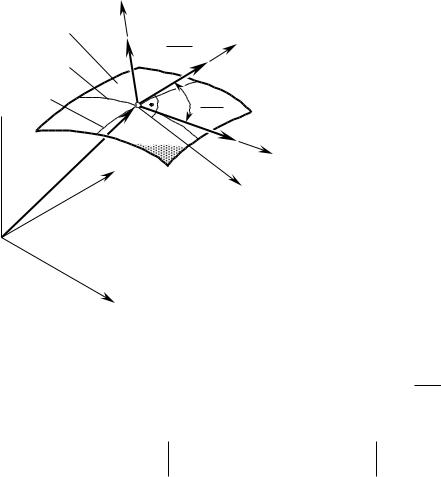
Взамкнутом цикле последовательных преобразований координат можно выделить прямое и обратное направление преобразования координат (рис. 4.1.).

Впрямом цикле (рис. 4.1.1) переход от системы коодинат XдYдZд детали первоначально производится к

локальной подвижной системе координат x K y K z K с началом в точке K касания поверхности Д детали и И инструмента. Такой переход осуществляется либо непосредственно оператором Res Д д , либо (например, когда заданная в своей системе координат XпдYпдZпд поверхность Д представляет собой

совокупность отдельных отсеков, каждый из которых задан в своей системе координат) через некоторые промежуточные системы координат Xпд.iYпд.i Zпд.i каждого из отдельных отсеков поверхости детали.

В обратном цикле последовательных преобразований координат (рис. 4.1.2) переход от системы координат XдYдZд детали первоначально производится в направление подвижной локальной системы

координат xиK yиK zиK с началом в точке K касания поверхности Д детали и И инструмента. Такой

переход описывается совокупностью операторов преобразований координат последовательно от одной к другой.

В замкнутом цикле последовательных преобразований координат составление операторов преобразования одной локальной системы координат xд yдzд в другую xи yи zи описывается, как правило,

проще.

Геометрическая информация о поверхности Д И может быть задана, например, ее уравнением (1.2):

в векторной форме.

1Конформный – от лат. conformis – подобный, соответствующий, сообразный.

В системе координат x K y K z K главные направления на поверхности Д находятся как корни квадратного уравнения (4).

Uд линией на ней.

Вслучае неортогональной параметризации поверхности Д угол ωд между осями x1 и y1 локальной

При построении системы координат x K y K z K следует обратить внимание на направление оси y K : устанавливая порядок сомножителей в векторном произведении исходных направляющих векторов надо