Radzevich, S.P. Monograph - 2001
.pdf
220 |
|
|
4. Геометрия касания поверхности детали и исходной инструментальной поверхности |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
R |
|
R |
|
|
|
|
1 tan 2 |
; |
|
|
c |
|
n |
; |
|
|
|
|
|
R |
|
. |
|
|
|||||||
|
|
|
|
1.д |
|
2.д |
|
|
|
|
|
|
arctan |
|
|
2.д |
|
|
|
||||||||||||||||||
|
|
|
k |
R |
|
|
R |
|
|
tan |
2 |
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
R |
|
tan |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.д |
|
|
|
|
|
|||||||||
|
|
|
|
2.д |
|
1.д |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Таким |
образом |
|
R |
|
R |
|
|
|
, |
R |
, , |
|
n |
|
|
|
|
|
|
T |
2.д |
|
|
|
|
|
|
|
|||||||||
|
|
R |
|
|
. |
|
|
|
|
T |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
1.и |
|
|
1.и |
1.д |
|
|
2.д |
|
k |
|
|
|
|
|
2.и |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Первый главный радиус кривизны R1.и |
поверхности И |
|
|
|
|
|
|
|
|
|
|
|
|
|
T1.и |
||||||||||||||||||||||
инструмента должен быть не только вещественным и |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
положительным, но и больше k . Следовательно, кроме |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
обычных |
условий |
существования |
|
вещественного |
и |
|
|
|
|
|
|
|
|
К |
|
|
|
|
T |
||||||||||||||||||
положительного корня, необходимо потребовать выпол- |
|
|
|
|
|
|
|
|
|
|
|
|
|
1.д |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
нение дополнительного условия, а именно, чтобы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 c 2 |
4c2 cot 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
1 c |
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
|
Sи |
|||||||||||||||
|
|
|
|
2(tan 2 c) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
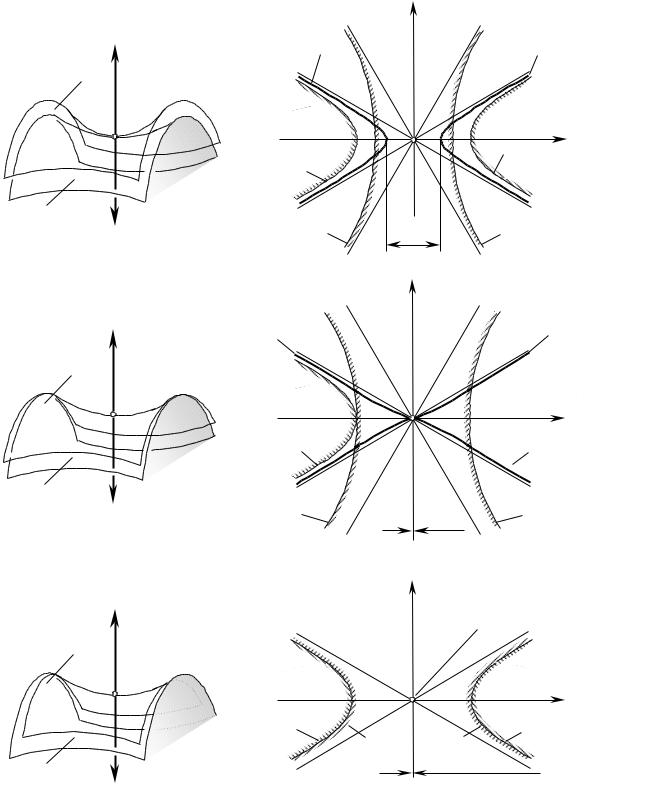
4.4.4. Квадратичная индикатриса Дюпена. |
Рас- |
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
V, , w |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
смотрим случай линейного касания поверхности детали |
Рис. 4.14. Квадратичные |
индикатрисы |
кривизны |
||||||||||||||||||||||||||||||||||
и исходной инструментмльной поверхности. |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
сопряженных поверхностей |
Д и И . |
||||||||||||||||||||||||||||
Поверхность |
Д |
может |
|
быть |
|
|
репараметризована |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
таким образом, что первые производные от rд |
по новым |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Uд и Vд |
параметрам имеют единичную длину, а новые параметрические Uд |
|
и Vд линии совпадают с |
||||||||||||||||||||||||||||||||||
линиями кривизны на |
Д . Тогда в точке K справедливы соотношения |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
(4.67) |
|
|
|
|
|
|
2rд N |
д |
k |
|
|
, |
2rд |
N |
д |
0 , |
|
2rд |
k |
2.д |
. |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
U |
|
2 |
|
|
1.д |
|
Uд Vд |
|
|
|
|
V2 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
д |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д |
|
|
|
|
|
|
|
|
|
|
Обозначим через угол между некоторым направлением |
|
rи |
на поверхности И и первым главным |
|||||||||||||||||||||||||||||
|
Uи |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
направлением T1.д |
и через |
|
угол между направлением |
|
|
|
|
(здесь w – параметр характеристики E |
||||||||||||||||||||||||
C w |
||||||||||||||||||||||||||||||||
поверхностей Д и И ) и тем же первым главным направлением T1.д |
(рис. 4.14). |
|
|
|
||||||||||||||||||||||||||||
Исходя из того, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
2rи |
n |
|
L |
; |
|
|
|
2rи |
n |
и |
M |
и |
; |
|
|
|
2rи |
n |
|
N |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
Uи Vи |
|
|
V2 |
|
|
||||||||||||||||
|
|
|
|
|
U 2 |
|
и |
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
и |
|||||||
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
и принимая во внимание, что вдоль характеристики E выполняются соотношения |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Nд w Nи w N w C N w , |
||||||||||||
|
Gд w Gи w G w C w C w , |
|
|
|||||||||||||||||||||||||||||
из (67) можно получить, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
2 |
rд |
|
|
|
|
|
|
|
2 |
rд |
|
|
|
|
2 |
rд |
|
|
|
|
|
|
G k1.д cos 2 |
k2.д sin 2 ; |
|||||
(4.68) |
N G |
|
cos2 |
|
2 |
|
|
cos sin |
|
|
sin 2 |
|
||||||||||||||||||||
|
|
|
Uд Vд |
V2 |
|
|||||||||||||||||||||||||||
|
|
U 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
д |
|
|
|
|
|
|
|
|
|
|
|
|
д |
|
|
|
|
|
|
|
|
|
|
|
|
||
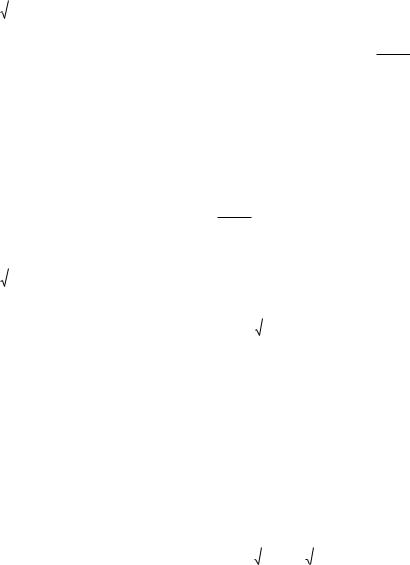

|
4.5. Мера степени конформности поверхности детали и исходной инструментальной поверхности |
|
223 |
||||||
n д |
|
|
|
|
4.5.1. Функции конформности. Для аналити- |
||||
|
|
|
|
ческого описания геометрии касания поверхностей |
|||||
|
|
|
Rи |
|
деталей и инструментов введем меру степени их |
||||
|
|
|
|
конформности, отражающую полноту прилегания |
|||||
Д |
|
|
Д |
И |
поверхности И инструмента к поверхности |
Д |
|||
|
И |
детали и особенности геометрии их касания в |
|||||||
К |
|
||||||||
|
|
|
|
дифференциальной окрестности точки K . |
|
|
|||
|
|
|
Rд |
|
Через контактную нормаль n д и (рис. 4.16.1) |
||||
|
|
|
|
проведем пучок секущих плоскостей. Каждая |
|||||
|
|
|
|
|
|||||
|
|
|
|
|
плоскость пучка пересекает поверхности Д |
и |
И |
||
|
1. |
|
2. |
|
по гладким кривым, касающимся одна другой в |
||||
|
|
|
точке K . Обозначим радиусы |
кривизны |
линий |
||||
|
|
|
|
|
|||||
Рис. 4.16. К определению индикатрисы конформности |
пересечения поверхностей |
Д и |
И текущей плос- |
||||||
поверхности |
И инструмента к поверхнос- |
костью пучка через Rд и |
Rи |
(рис. 4.16.2). Кон- |
|||||
ти |
Д обрабатываемой детали. |
|
формные свойства поверхностей |
Д и И опреде- |
|||||
|
|
|
|
|
|||||
|
|
|
|
|
ляются алгебраическими значениями радиусов кри- |
||||
визны Rд и |
Rи . Для однозначного аналитического описания геометрии касания поверхностей Д |
и |
И |
||||||
используем аналитический функционал от Rд |
и Rи , |
для которого не существует такого согласованного |
|||||||
между собой изменения аргументов, при котором для разных значений аргументов функционал тождественен сам себе. Функционалы такого класса назовем функциями (функционалами) конформности. В общем виде они записываются так:
rconf |
F f1 Rд ; f2 Rи , |
(4.75) |
|
где f1 Rд –нелинейная функция от Rд ; |
|
|
|
f2 Rи –нелинейная функция от Rи ; |
|
|
|
F – произвольный функционал. |
|
|
|
В частных случаях функции f1 Rд |
и |
f2 Rи могут быть из одного класса функций, в том числе они |
|
могут быть одинаковыми (т.е. иметь вид |
f Rд и f Rи ). |
|
|
Определение 4.3. Функция конформности – это сложная функция (функционал) двух нелинейных функций, зависящих от алгебраических значений нормальных радиусов кривизны Rд и Rи поверхностей Д и
И в точке K их касания, для которого не существует такого согласованного между собой изменения аргументов, при котором для разных значений аргументов функционал тождественен сам себе.
При изменении отношения dUд (т.е. при вращении секущей плоскости вокруг контактной нормали) dVд
аргументы Rд и Rи изменяются по величине, а соответствующее им значение функции конформности количественно отражает конформные свойства поверхностей Д и И в текущем положении секущей
плоскости.
Текущее положение плоского нормального сечения удобно определить центральным углом , который это сечение образует с первым главным сечением C1.д поверхности Д .
С учетом того, что Rд Rд и Rи Rи , функционал (75) преобразуется к виду
|
|
|
|
r |
conf . |
F |
|
f |
* ; |
f * , |
(4.76) |
|
|
|
|
|
|
|
1 |
2 |
|
||
где функции f * |
, |
f |
* |
аналогичны функциям |
f , |
f |
2 |
в уравнении (75). |
|
||
1 |
|
|
2 |
|
|
1 |
|
|
|
Д и И однозначно. |
|
Все функции класса (76) описывают геометрию касания поверхностей |
|||||||||||
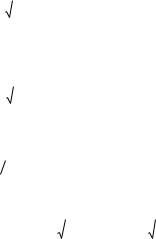
224 |
4. Геометрия касания поверхности детали и исходной инструментальной поверхности |
|
|
|||
|
Поскольку функционал F f * ; f |
* |
зависит от двух нелинейных функций |
f * |
и f * , он всегда |
|
|
1 |
2 |
|
|
1 |
2 |
нелинеен (за исключением случая, когда, во-первых, f * тождественно равно |
f * |
) и, во-вторых, имеет |
||||
|
|
|
1 |
2 |
|
поверхности И |
экстремумы, соответствующие экстремальным значениям степени конформности |
||||||
инструмента к поверхности Д детали. |
|
|
|
|
|
|
Для решения задачи синтеза наивыгоднейшего формообразования поверхности детали из класса функций конформности можно использовать любую функцию – каждая из них однозначно описывает геометрию касания поверхностей Д и И в дифференциальной окрестности точки K . Целесообразно
выбрать функционал F возможно более простой структуры, не имеющий локальных экстремумов и обладающий другими полезными свойствами (см. ниже).
4.5.2. Индикатриса конформности. Для решении задачи синтеза наивыгоднейшего формообразования поверхности детали удобно использовать частный случай функции конформности (76), а именно – индикатрису конформности поверхности детали и исходной инструментальной поверхности (Радзевич С.П.,
1987, 1988).
Чтобы получить уравнение этой характеристической кривой, рассмотрим дифференциальные окрестности точки K на поверхности Д детали и на поверхности И инструмента. Для этого с точкой K
свяжем начало локальной системы координат xд yд .
Распределение нормальных кривизн поверхности Д в дифференциальной окрестности точки K описывается индикатрисой кривизны Ind Д (44):
(4.77) |
|
|
|
|
|
Lд |
|
x2 |
|
2Mд |
|
x y |
|
|
Nд |
|
y2 |
1 . |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
Eд |
|
|
д |
|
|
EдGд |
|
д д |
|
|
|
|
Gд |
|
д |
|
|
|
|
|
|
|
|||||
Аралогичным уравнением (44): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
(4.78) |
|
|
|
|
|
Lи |
|
x2 |
|
|
2Mи |
|
x y |
|
Nи |
|
y2 |
1 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
Eи |
|
|
и |
|
|
EиGи |
|
и и |
|
|
|
|
|
Gи |
|
и |
|
|
|
|
|
|
|
||||
индикатрисы |
кривизны |
Ind И |
|
описывается |
распределение |
|
нормальных кривизн поверхности И в |
||||||||||||||||||||||||||
дифференциальной окрестности точки K на ней. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Индикатрису конформности |
|
Indconf Д И |
поверхностей |
|
Д |
и |
И |
|
определим как плоскую кривую, |
||||||||||||||||||||||||
радиус-вектор rconf каждой точки которой равен алгебраической сумме |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sgn Φ 1 |
|
|
|
|
|
|
sgn Φ 1 . |
|||||||||||
(4.79) |
r |
conf |
r |
д |
sgn R |
r |
sgn R |
|
|
R |
|
|
|
|
|
|
R |
|
|
||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
д |
|
и |
|
|
и |
|
|
|
|
д |
|
|
|
|
|
|
|
2.д |
|
|
|
и |
|
|
2.и |
|||
Формула (79) находится в соответствии с (76) – следовательно, индикатриса конформности Indconf Д И принадлежит к классу функций конформности (75). Второй сомножитель каждого слагаемого в
И принадлежит к классу функций конформности (75). Второй сомножитель каждого слагаемого в
(79) – функция-знак, не изменяет величин rд и rи , он определяет их знак с учетом характера кривизны плоских нормальных сечений поверхностей Д и И в точке K : “+” – для выпуклых и “–“ – для вогнутых нормальных сечений этих поверхностей.
Чтобы воспользоваться уравнениями (77) и (78) индикатрис кривизны Ind Д и Ind И , необходимо эти
уравнения, во-первых, записать в общей системе декартовых координат, и, во-вторых, перейти к общей системе полярных координат.
В процессе обработки инструмент занимает различные положения относительно детали – ориентация поверхности И относительно поверхности Д изменяется во времени. Более того, в фиксированной точке К
инструмент имеет одну степень подвижности относительно детали – возможность поворота вокруг контактной нормали (см. гл. 3, раздел 2.3. “Ориентирующие движения инструмента”). Поэтому в общем
случае поверхности Д и И занимают такое положение одна относительно другой, в котором их первые главные секущие плоскости C1.д и C1.и образуют угол относительной локальной ориентации.

|
|
|
|
|
|
|
4.5. Мера степени конформности поверхности детали и исходной инструментальной поверхности |
|
|
|
225 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Чтобы записать уравнения (77) и (78) в общей системе декартовых координат, достаточно уравнение (78) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
привести к локальной системе координат |
xд yд |
|
|
детали. Для этого воспользуемся оператором Res Kи K |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
преобразования координат (12). После приведения (78) примет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
L |
|
|
|
M |
и |
|
|
|
|
|
|
N |
и |
|
|
|
|
|
2 |
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
2M |
и |
|
|
|
|
|
|
|
|
|
|
|
|
N |
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
и |
cos2 |
|
|
|
sin 2 |
|
|
|
sin 2 x |
|
|
|
и |
|
sin 2 |
|
|
|
|
|
|
|
|
cos 2 |
|
|
|
sin 2 x |
y |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Eи |
|
|
|
EиGи |
|
|
|
|
|
|
Gи |
|
|
|
|
|
д |
|
|
|
Eи |
|
|
|
|
|
|
|
|
|
|
|
|
EиGи |
|
|
|
|
|
|
|
|
|
|
|
Gи |
|
|
|
|
|
|
|
|
д |
д |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.80) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
M |
и |
|
|
|
|
|
|
|
|
|
N |
и |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
sin |
2 |
|
|
|
|
|
|
|
sin 2 |
|
cos2 |
y |
2 1. |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Eи |
|
|
|
|
|
|
|
|
|
|
|
EиGи |
|
|
|
|
|
|
Gи |
|
|
|
|
|
д |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Уравнения (77) и (80) индикатрис кривизны Ind Д и Ind И представлены в общей системе координат |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
xд yд . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Для перехода к полярным координатам воспользуемся формулами (3.30). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
После преобразований из (77) и (80) соответственно получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
rд |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EдGд |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.81) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos2 M |
|
|
|
|
|
|
|
|
|
|
|
|
sin 2 N |
|
|
|
|
|
sin 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L G |
д |
д |
|
E |
д |
G |
д |
д |
E |
д |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
rи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EиGи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
(4.82) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
cos2 |
M |
|
|
|
|
|
|
|
|
|
|
sin 2 N |
|
|
|
sin 2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
L G |
и |
и |
|
E |
и |
G |
и |
|
и |
E |
и |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Подставляя (81) и (82) в (79), приходим к результату: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
rconf |
|
|
|
|
|
|
|
|
|
|
EдGд |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sgnΦ2.1д |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
cos2 M |
|
|
|
|
|
|
|
|
|
|
|
|
sin 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
L G |
д |
д |
|
E |
д |
G |
д |
|
sin 2 N |
д |
E |
д |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
д |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.83) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EиGи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sgnΦ2.и . |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 M |
|
|
|
|
|
|
|
|
|
|
|
sin 2 N |
|
|
|
|
|
sin 2 |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L G |
и |
cos |
и |
|
E |
и |
G |
и |
и |
E |
и |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Уравнение (83) является уравнением характеристической |
|
|
кривой |
|
|
– |
|
индикатрисы |
конформности |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Indconf Д / И |
первого рода поверхности детали и исходной инструментальной поверхности. Анализ этого |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
уравнения показывает, что в общем случае индикатриса конформности |
|
Indconf Д / И |
является плоской |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
кривой четвертого порядка. Она обладает центральной и, в частных случаях (когда угол |
|
локальной |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ориентации кратен 0,5 ) зеркальной |
симметрией. |
Свойство |
центральной симметрии |
индикатрисы |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
конформности |
|
Indconf Д / И |
|
позволяет |
|
без |
|
|
|
потери |
информации |
рассматривать |
|
ее |
|
|
в |
пределах не |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
центрального угла 2 , а в пределах центрального угла и тем самым уменьшить занимаемый объем памяти ЭВМ и системы ЧПУ металлорежущим станком. Если же в каждой точке касания поверхностей Д и И эта характеристическая кривая дополнительно обладает зеркальной симметрией, угол может быть уменьшен еще в два раза 0,5 .
Индикатриса конформности Indconf Д / И инвариантна относительно характера параметризации
поверхностей Д и И – при изменении параметризации изменяется уравнение этой кривой, но не ее форма и параметры. Параметры Indconf Д / И не зависят от величин углов д и между координатными Uд и и
Vд и линиями, но зависят от относительной ориентации контактирующих поверхностей Д и И .

226 |
4. Геометрия касания поверхности детали и исходной инструментальной поверхности |
Если |
поверхности Д и И параметризованы ортогонально, то при выводе уравнения (83) можно |
исходить не из уравнений (44) индикатрис кривизны Ind Д И , а из более простых уравнений (45) – это приведет к получению более простого уравнения индикатрисы конформности Indconf Д / И , которое можно
рассматривать как частный случай уравнения (83).
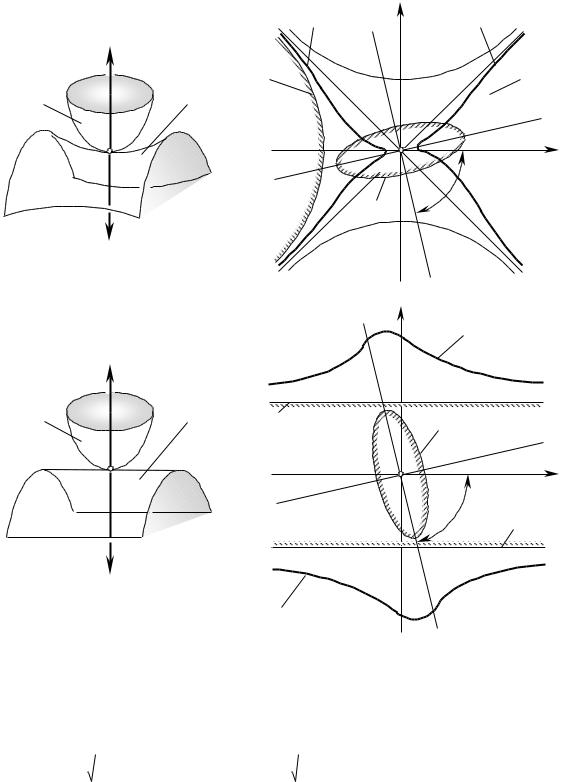
На рис. 4.17 приведены примеры индикатрис конформности Indconf Д / И для случаев касания гладких
регулярных локальных участков поверхностей Д и И : выпуклого эллиптического локального участка
поверхности И инструмента с гиперболическим (рис. 4.17.1) и выпуклым параболическим (рис. 4.17.2) локальным участком поверхности Д детали; показаны соответствующие индикатрисы кривизны и
характерные параметры формы контактирующих поверхностей.
Индикатриса конформности Indconf Д И (83) тесно связана со вторыми основными квадратичными формами Φ2.д и поверхностей Д и И .
И (83) тесно связана со вторыми основными квадратичными формами Φ2.д и поверхностей Д и И .
Параметры индикатрисы конформности (83) требуется расчитывать в большом количестве точек касания поверхностей Д и И . В случаях, когда достаточно знать параметры этой характеристической кривой в
локальной системе координат, связанной с деталью, с помощью операторов преобразования координат (см. гл. 3) уравнение (83) можно из любой системы координат преобразовать в локальную подвижную систему координат. Можно поступить иначе и вывести уравнение уравнение этой характеристической кривой непосредственно в локальной подвижной системе координат. Для этого исходим из формулы Эйлера (30),
которую для поверхности |
Д детали и отдельно для поверхности И инструмента представим в такой форме: |
|||||||||||||||||||
Rд |
|
|
R1.дR2.д |
|
|
|
|
; |
Rи |
|
|
R1.иR2.и |
|
cos2 . |
||||||
R |
|
sin 2 R |
|
cos2 |
R |
sin 2 R |
|
|||||||||||||
|
|
|
1.д |
2.д |
|
|
|
|
|
|
|
1.и |
|
2.и |
|
|
|
|||
Подставив эти значения Rд и Rи |
нормальных радиусов кривизны в (79), получим: |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R1.дR2.д |
|
|
|
|
1 |
|
|
|
|
R1.иR2.и |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
rconf |
|
|
|
|
sgn Φ2.д |
|
|
|
|
|
sgnΦ2.и . |
|||||||||
R |
sin 2 R |
cos2 |
|
R |
sin |
2 μ R |
cos2 μ |
|||||||||||||
|
|
|
1.д |
|
2.д |
|
|
|
|
|
|
1.и |
|
2.и |
|
|
|
|
|
|
Это уравнение эквивалентно уравнению (83) индикатрисы конформности |
Indconf Д И , но записано в |
|||||||||||||||||||
подвижной локальной системе координат, связанной с поверхностью Д детали.
Уравнение (83) может быть переписано в матричной форме. Для этого окажется полезным приведенное выше матричное уравнение (50) индикатрисы кривизны поверхностей Д И .
Подобно тому, как наряду с индикатрисой кривизны (индикатрисой Дюпена) (44) выше в рассмотрение введена индикатриса собственно кривизны (54), так и наряду с уравнением (83) индикатрисы конформности
Indconf Д И , построенном исходя из соотношений радиусов кривизны поверхностей Д и И (см. (79)), можно ввести в рассмотрение индикатрису конформности второго рода, построенную исходя из соотношений
И , построенном исходя из соотношений радиусов кривизны поверхностей Д и И (см. (79)), можно ввести в рассмотрение индикатрису конформности второго рода, построенную исходя из соотношений
собственно кривизн поверхностей |
Д и И . По аналогии с (79) индикатрису конформности второго рода |
|||||||||||||
Ind k |
Д / И определим как: |
|
|
|
|
|
|
|
|
|
|
|
|
|
conf |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.84) |
|
kconf |
|
kд |
|
|
sgn kд |
|
kи |
|
|
sgn kи . |
||
|
|
|
|
|
||||||||||
В рассматриваемом случае удобно воспользоваться формулой Эйлера (30), которую запишем для
поверхности Д детали и для поверхности И инструмента |
|
|
|
|
||||||||||
k |
д |
k |
cos2 k |
2.д |
sin 2 |
|
; |
k |
и |
k |
cos2 k |
2.и |
sin 2 |
. |
|
1.д |
|
|
|
|
|
1.и |
|
|
|
||||
4.5. Мера степени конформности поверхности детали и исходной инструментальной поверхности |
227 |
|
Indconf ( Д / И) |
yд |
Indconf ( Д / И) |
n д |
|
|
|
|
Ind Д |
|
Ind Д |
И |
Д |
|
|
|
C1.д |
|
xд |
K |
|
K |
|
|
C2.u |
Ind И |
|
|
|
|
|
nu |
|
|
|
|
|
C2.д |
C1.u |
|
1. |
|
|
|
|
yд |
Indconf ( Д / И) |
|
n д |
|
|
|
|
|
|
|
И |
|
D |
Ind |
Д |
|
|
Ind И |
|
|
|
|
|
|
|
|||
|
|
|
C1.д |
|
|
K |
|
xд |
|
K |
|
|
|
|
|
|
|
|
|
|
C2.u |
|
|
|
Ind Д |
|
|
n u |
|
|
|
|
|
|
|
|
2. |
|
Indconf |
( Д / И) |
C2.д |
C1.u |
|
|
|
|
|
|
|||||
Рис. 2.17. Примеры индикатрис конформности Indconf Д / И для случаев касания выпуклого
эллиптического локального участка поверхности И инструмента с гиперболическим
(1) и выпуклым параболическим (2) локальным участком поверхности Д детали.
Подставив эти значения kд |
и kи |
в (84), получим |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sgn Φ 1 . |
|
||
k |
conf |
|
|
k |
cos2 k |
2.д |
sin |
2 |
|
|
sgn Φ 1 |
|
|
k |
cos |
2 k |
2.и |
sin |
2 |
|
|
(4.85) |
|||
|
|
|
|
||||||||||||||||||||||
|
|
|
|
1.д |
|
|
|
|
|
2.д |
|
|
|
1.и |
|
|
|
|
|
|
2.и |
|
|||