
Radzevich, S.P. Monograph - 2001
.pdf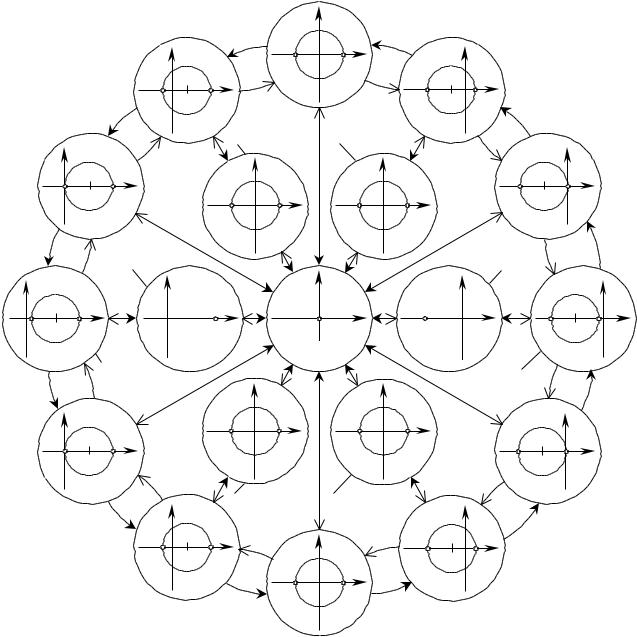
100 |
1. Рабочие поверхности деталей и инструментов. |
|
|
Минимальный |
|
|
|
|
|
Гиперболический |
|
tд и |
|
|
|
Гиперболический |
|
|
|
C |
|
|
|
||
псевдовыпуклый |
|
|
tд и |
|
псевдовогнутый |
|
|
|
|
|
|
|
|||
tд и |
|
|
kд и |
|
|
|
|
|
|
|
|
|
|
||
|
C |
|
C |
|
|
|
|
|
|
|
|
|
|
||
Выпуклый |
|
kд и |
|
|
kд и |
Вогнутый |
|
параболический |
|
|
|
параболический |
|||
|
|
|
|
|
|||
|
|
Минимальный |
Минимальный |
|
|
|
|
tд и |
|
|
|
|
|
tд и |
|
C |
|
tд и |
tд и |
|
|
C |
|
k |
|
C |
C |
|
|
kд и |
|
д и |
|
|
|
|
|
|
|
|
|
kд и |
|
kд и |
|
|
|
Выпуклый |
|
|
|
|
Вогнутый |
|
|
омбилический |
|
|
|
|
омбилический |
|
|
tд и |
tд и |
tд и |
|
tд и |
|
tд и |
|
C |
|
|
|
|
|
C |
|
kд и |
|
kд и |
kд и |
|
kд и |
|
kд и |
|
|
Уплощения |
|
|
|
|
|
Выпуклый |
Вогнутый |
эллиптический |
tд и |
tд и |
эллиптический |
|
tд и |
|
C |
C |
tд и |
C |
|
kд и |
kд и |
C |
|
|
|
||
kд и |
|
|
|
kд и |
|
|
Минимальный |
Минимальный |
|
Выпуклый |
tд и |
|
tд и |
Вогнутый |
параболический |
|
C |
C |
параболический |
|
|
|
||
|
|
tд и |
|
|
|
|
kд и |
C |
kд и |
|
|
|
|
|
Гиперболический |
|
|
kд и |
Гиперболический |
псевдовыпуклый |
|
|
|
псевдовогнутый |
|
|
Минимальный |
|
|
Рис. 1.27. Взаимосвязь между различного типа локальными участками гладких регулярных поверхностей Д И : круговые диаграммы.
1.3. О классификации рабочих поверхностей деталей и инструментов |
101 |
|
|
|
Минимальный |
|
|
|
|
|
|
yд u |
|
|
|
Гиперболический |
|
|
|
|
|
Гиперболический |
псевдовыпуклый |
yд u |
|
|
|
yд u |
псевдовогнутый |
|
|
|
xд u |
|
|
|
Выпуклый |
|
xд u |
|
|
xд u |
Вогнутый |
параболический |
|
Минимальный |
Минимальный |
|
параболический |
|
|
|
|
|
|||
yд u |
|
yд u |
|
yд u |
|
yд u |
|
|
|
|
|
||
xд u |
|
|
|
|
|
xд u |
|
|
xд u |
|
xд u |
|
|
|
|
|
|
|
||
Выпуклый |
|
|
|
Вогнутый |
||
омбилический |
|
|
|
омбилический |
||
yд u |
yд u |
|
Индикатриса |
yд u |
yд u |
|
|
|
|
|
|
||
|
|
|
кривизны |
|
|
|
д u |
|
xд u |
несуществует |
xд u |
д u |
|
|
|
|
||||
|
|
|
Уплощения |
|
|
|
Выпуклый |
yд u |
|
yд u |
Вогнутый |
||
эллиптический |
|
эллиптический |
||||
yд u |
|
|
|
|
|
yд u |
|
|
|
xд u |
|
xд u |
xд u |
xд u |
|
|
|
|
|
|
|
|
|
|
|
|
|
Выпуклый |
yд u |
Минимальный |
Минимальный |
yд u |
Вогнутый |
|
|
|
|
|
|||
параболический |
|
|
|
|
параболический |
|
|
|
yд u |
|
|
||
|
|
|
|
|
|
|
|
|
xд u |
|
|
xд u |
|
Гиперболический |
|
|
|
xд u |
|
Гиперболический |
|
|
|
|
|
||
псевдовыпуклый |
|
|
|
|
|
псевдовогнутый |
Минимальный
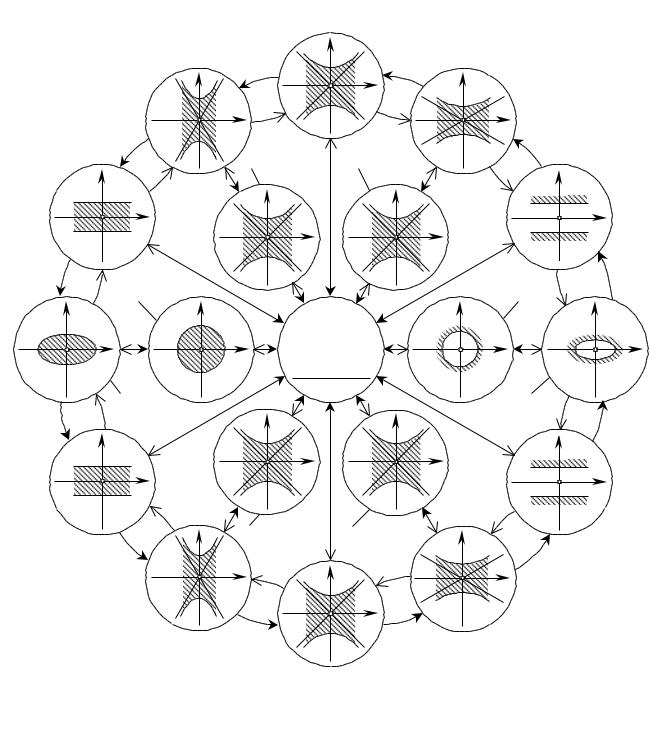
Рис. 1.28. Взаимосвязь между различного типа локальными участками гладких регулярных поверхностей Д И : индикатрисы кривизны (индикатрисы Дюпена).
102 |
|
|
1. Рабочие поверхности деталей и инструментов |
|
|
|
|
|||
|
|
|
|
Минимальный |
|
|
|
|
|
|
|
Гиперболический |
|
|
Д И |
n д u |
|
|
Гиперболический |
||
|
|
|
|
|
|
|||||
|
псевдовыпуклый |
|
|
|
|
|
псевдовогнутый |
|
||
|
|
n д u |
|
|
|
|
|
|||
|
|
Д И |
|
M |
Д И |
n д u |
|
|
||
|
|
|
|
|
|
|
|
|||
Выпуклый |
|
M |
|
|
|
|
M |
Вогнутый |
||
параболический |
|
|
|
|
|
|
|
параболический |
||
|
|
|
Минимальный |
Минимальный |
|
|
|
|
||
|
n д u |
|
|
|
|
|
|
Д И |
n д u |
|
|
Д И |
|
|
n д u |
|
n д u |
|
|
|
|
|
M |
|
Д И |
Д И |
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
|
|
|
|
M |
|
M |
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
Выпуклый |
|
|
|
|
|
Вогнутый |
|
|
|
|
омбилический |
|
|
|
|
|
омбилический |
|
|
|
Д И |
n д u |
Д И |
n д u |
Д И |
n д u |
Д |
И |
n д u |
Д И |
n д u |
|
|
|
|
|
||||||
|
M |
|
M |
|
M |
|
|
|
|
|
|
|
|
|
Уплощения |
|
M |
|
M |
|
|
|
Выпуклый |
|
|
|
|
Вогнутый |
|
|||
|
эллиптический |
|
n д u |
|
n д u |
|
эллиптический |
|
|
|
|
|
|
Д И |
Д И |
|
|
|
|
||
|
n д u |
|
|
|
|
Д И |
n д u |
|
||
|
|
|
|
|
|
|
|
|||
|
Д И |
|
|
M |
|
M |
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
Минимальный |
Минимальный |
|
|
M |
|
||
Выпуклый |
|
|
|
Вогнутый |
||||||
Д И |
n д u |
|
|
Д И |
n д u |
|||||
параболический |
|
|
параболический |
|||||||
|
|
|
|
|||||||
|
|
|
M |
Д И |
n д u |
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Гиперболический |
|
|
|
M |
|
|
Гиперболический |
||
|
|
|
|
|
|
|
||||
|
псевдовыпуклый |
|
|
|
|
|
|
псевдовогнутый |
|
|
|
|
|
|
Минимальный |
|
|
|
|
|
|
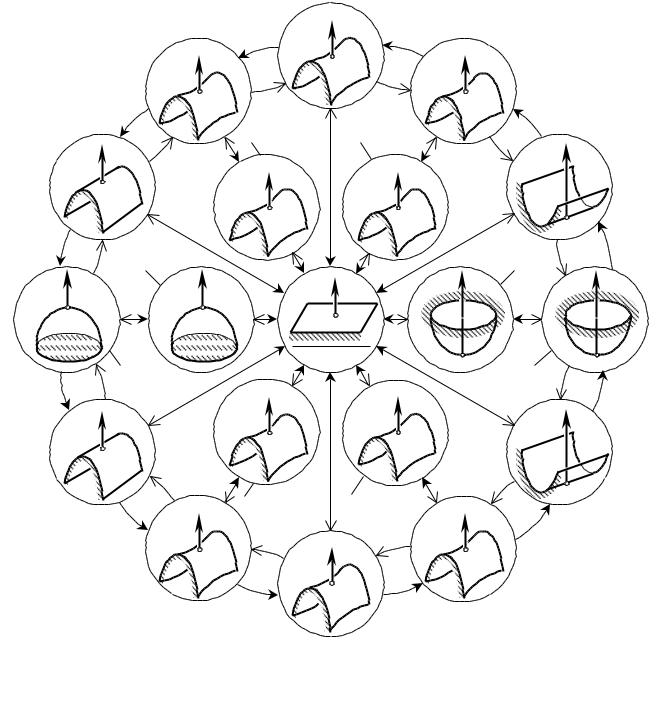
Рис. 1.29. Взаимосвязь между различного типа локальными участками гладких регулярных поверхностей |
||||||||||
|
Д И : схемы локальных участков. |
|
|
|
|
|
|
|
||
1.3. О классификации рабочих поверхностей деталей и инструментов |
103 |
||
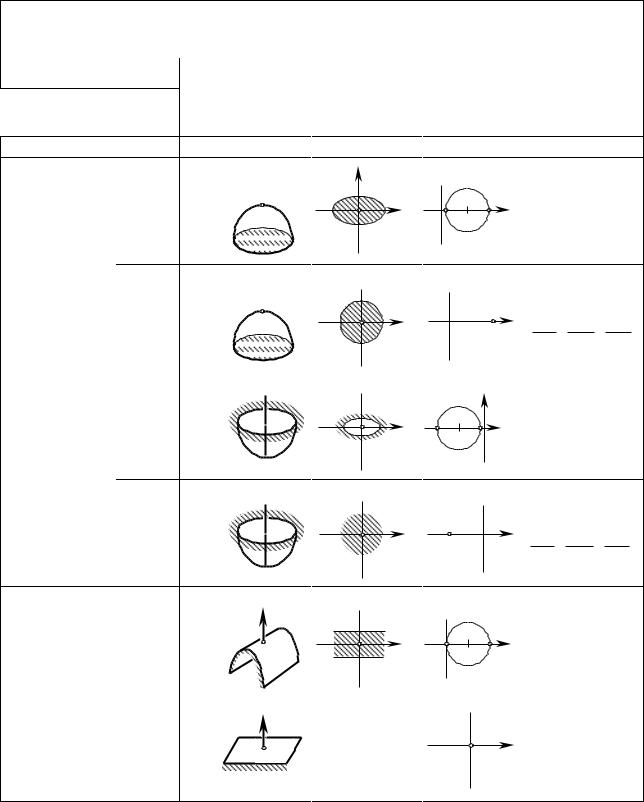
Гладкие регулярные локальные участки поверхности Д И сложной формы |
Таблица 1.1. |
||
|
|||
Тип локального участка |
Характеристика локального участка поверхности |
Д И |
|
поверхности Д И |
|||
|
|
||
кривизна
 полная
полная  средняя
средняя 
(гауссова)
1 2
~
Mд u 0
~
Gд u 0
~
Mд u 0
~
Mд u 0
~
Gд u 0
~
Mд u 0
cоотнош |
название |
|||
|
||||
k1 и k2 |
|
|
||
|
3 |
|
|
4 |
k1 k2 |
|
0 |
Выпуклый эллиптический |
|
|
||||
k1 |
k2 |
0 |
Выпуклый омбилиический |
|
|
||||
k1 |
k2 |
0 |
Вогнутый эллиптический |
|
|
||||
k1 |
k2 |
0 |
Вогнутый омбилиический |
|
|
||||
k1 k2 |
0 |
Выпуклый параболический |
||
|
||||
вид
локального
участка
5
Д И 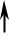 n д u
n д u
M
Д И 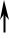 n д u
n д u
M
Д И 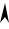 n д u
n д u
M

ДИ 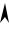 n д u
n д u
M

n д u
Д И
M
|
|
Уплощения |
Д И |
n д u |
|
|
|
||
k1 k2 |
0 |
|
|
M |
индикатриса
кривизны
6 |
yд u |
xд u |
yд u 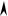
xд u
yд u 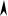
xд u
yд u 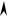
 д u
д u
yд u 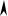
xд u |
Индикатриса кривизны не существует
круговая
диаграмма
7
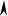 tд и
tд и
C
kд и
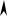 tд и
tд и
kд и
tд и |
C |
kд и |
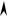 tд и
tд и
kд и
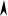 tд и
tд и
C
kд и
tд и 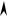

kд и
аналитический
признак
8
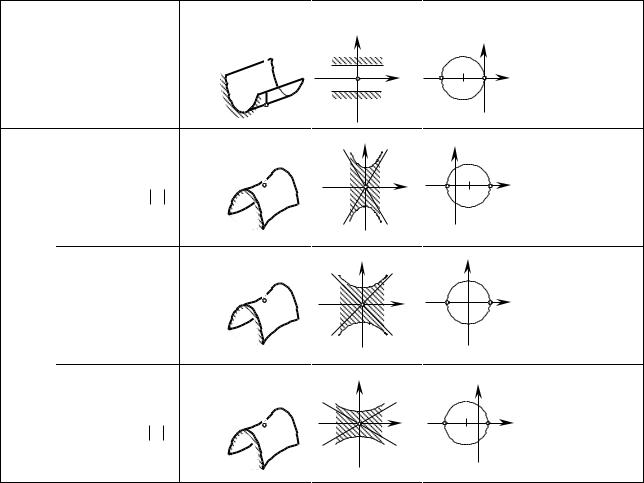
Lд u Nд u Mд2 u 0
Lд u Nд u Mд2 u 0
Eд u Fд u Gд u Lд u Mд u Nд u
Lд u Nд u Mд2 u 0
Lд u Nд u Mд2 u 0
Eд u Fд u Gд u Lд u Mд u Nд u
Lд u Nд u Mд2 u 0
Lд u Nд u Mд2 u 0 Lд u Nд u Mд2 u
104 |
1. Рабочие поверхности деталей и инструментов |
1 |
2 |
~ |
~ |
Gд u 0 |
Mд u 0 |
~
Mд u 0
~ |
~ |
Gд u 0 |
Mд u 0 |
~
Mд u 0
3
k1 0 k2
k1 k2 k1 k2
k1 k2
k1 k2 k1 k2
4
Вогнутый |
параболический |
Гиперболический |
псевдовыпуклый |
Минимальный |
|
Гиперболический |
псевдовогнутый |
5
Д И 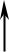 nд u
nд u
M
Д И  nд u
nд u
M
Д И  nд u
nд u
M
Д И  nд u
nд u
M
6 |
7 |
|
yд u |
tд и |
|
|
||
|
C |
|
xд u |
kд и |
|
yд u |
tд и |
|
C |
||
|
||
xд u |
kд и |
|
yд u |
tд и |
|
|
C |
|
xд u |
kд и |
|
yд u |
tд и |
|
|
C |
|
xд u |
kд и |
8
Lд u Nд u Mд2 u 0
Lд u Nд u Mд2 u 0
Lд u Nд u Mд2 u 0
Lд u Nд u Mд2 u 0
Краткая историческая справка. В исследованиях геометрии поверхностей круговые диаграммы впервые были применены, по-видимому, R.Miron (1958). Они использовались I.Vaisman (1959) для графической интерпретации свойств поверхностей Вейнгартена. Из более поздних публикаций по этому вопросу следует указать на работы P.Lowe (1980, 1982), A.Nutbourne (1986), на монографии A.Nutbourne and R.Martine (1988) и
C.Calladine (1983). Тем не менее историю применения круговых диаграмм в различных технических приложениях следует начинать с изучения трудов Х.О. Мора (Mohr, H.O.).
1.3.3. Типы локальных участков поверхности Д(И). На поверхностях деталей и инструментов можно выделить локальные участки следующих видов.
1.3.3.1. Гладкие регулярные локальные участки поверхности Д(И). В каждой неособой точке гладкой регулярной (следовательно, дважды непрерывно дифференцируемой) поверхности Д И существует (причем
единственный) соприкасающийся параболоид. Гладкие регулярные локальные участки поверхности Д И
удобно различать по типу соприкасающегося в рассматриваемой точке поверхности параболоида, в окрестности которой он расположен. Соприкасающийся параболоид определяет форму локального участка сложной
поверхности Д И в окрестности обыкновенной точки на ней.
Кривизна поверхности Д И в текущей ее точке M рассматривается как кривизна соответствующей линии на этой поверхности. Если через точку M провести нормаль N д и к поверхности Д И , через которую
проходит пучок секущих плоскостей, то кривизна линий пересечения поверхности плоскостями этого пучка в общем случае не будет одинаковой для разных нормальных сечений. Те плоские нормальные сечения C1.д и
и C2.д и , в которых кривизна линий пересечения поверхности Д И принимает соответственно минимальное
1.3. О классификации рабочих поверхностей деталей и инструментов |
105 |
и максимальное значения, являются главными секущими плоскостями, а соответствующие им кривизны k1.д и и k2.д и – главными кривизнами поверхности Д И . Главные кривизны поверхности находятся как
корни характеристического уравнения (Struik, D.J., 1961):
|
Lд и Eд и kд и |
Mд и Fд и kд и |
|
0, |
|
|
|||
|
Mд и Fд и kд и |
Nд и Gд и kд и |
|
|
а для вычисления их значения удобно воспользоваться квадратным уравнением, получаемым после раскрытия этого определителя:
E |
|
G |
F 2 |
k2 |
E |
|
N |
|
|
|
|
2F |
|
|
|
M |
д и |
G |
|
|
|
|
|
L |
|
|
k |
д и |
L |
|
|
N |
д и |
M |
2 |
|
0. |
(1.109) |
||||||||||||||||||||||||||||
|
д и д и |
д и |
д и |
|
|
|
д и д и |
|
|
|
|
|
|
д и |
|
|
|
|
|
|
|
д и |
|
д и |
|
|
|
|
д и |
|
|
|
|
д и |
|
|
|
|||||||||||||||||||||||||||||
Главные радиусы кривизны R1.д и и |
|
R2.д и |
|
– величины, обратные главным кривизнам k1.д и |
и k2.д и |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
соответствтенно R1.д и k1.1д и |
|
и R2.д и k2.1д и |
|
|
удобно находить как корни квадратного уравнения: |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
L |
|
N |
M 2 |
R2 |
|
E |
|
N |
д и |
2F |
|
|
|
M |
д и |
G |
|
|
|
|
L |
|
|
|
R |
|
|
|
E |
д и |
G |
|
F |
2 |
|
0. |
(1.110) |
|||||||||||||||||||||||||||||
д и д и |
д и |
д и |
|
|
|
д и |
|
|
|
|
|
|
д и |
|
|
|
|
|
|
|
|
д и |
д и |
|
д и |
|
|
|
|
д и |
|
|
д и |
|
|
|
||||||||||||||||||||||||||||||
Первая главная кривизна |
k1.д и |
|
поверхности |
|
Д И |
|
|
|
измеряется в первом главном сечении |
C1.д и |
и |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
имеет большее алгебраическое значение, а вторая главная кривизна |
|
k2.д и |
|
– измеряется во втором главном |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
сечении C2.д и – ее алгебраическое значение меньше. При таком допущении радиус кривизны R1.д и первого |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
главного сечения C1.д и поверхности |
Д И |
|
будет меньшим, |
а радиус кривизны R2.д и |
второго главного |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
сечения C2.д и – большим. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д И |
|
|
|
|
|||||||
Радиус кривизны текущего плоского нормального сечения Cд и |
поверхности |
расчитывается по |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
формуле: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Φ1.д и |
|
E |
д и |
dU 2 |
|
|
|
2F |
д и |
dU |
д и |
dV |
|
|
G |
д и |
dV2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
д и |
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
|
|
|
|
д и |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
Rд и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
Φ2.д и |
|
L |
|
|
|
|
dU |
2 |
|
|
|
2M |
д и |
dU |
д и |
dV |
|
|
N |
д и |
dV2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
|
|
|
|
д и |
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
|
|
|
|
д и |
|
|
|
|
|
|||||||||||||||||||||||
Пример 1.5. Рабочая поверхность |
|
Д детали представляет собой гиперболический параболоид, заданный в декартовой системе |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
координат (рис. 1.30) уравнением |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
Xд2 |
|
|
Yд2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д |
|
|
|
4 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Требуется определить основные элементы локальной геометрии поверхности |
|
|
Д : касательную плоскость, нормаль, коэффициенты |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
первых двух основных квадратичных форм, главные радиусы кривизны. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
Преобразуем уравнение поверхности |
Д в параметрическую форму. |
|
Поскольку гиперболический параболоид является линейчатой |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
поверхностью, то в данном случае в качестве координатных |
Uд |
|
и Vд линий |
удобно принять |
|
линии |
на поверхности |
Д , |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
удовлетворяющие двум условиям: |
|
|
|
|
Д |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
– первое семейство прямых линий на |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
X |
д |
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
д |
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д |
U |
д |
; |
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
д |
Z |
д |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
д |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
X |
д |
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
д |
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д |
U |
д |
; |
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
д |
Z |
д |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
д |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
– второе семейство прямых линий на |
Д |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||

106 |
1. Рабочие поверхности деталей и инструментов |
|
|
|
|
|
|
|
|
|
|||||
Zд |
|
X |
д |
|
Y |
|
|
X |
д |
|
Y |
|
. |
|
|
|
|
д V ; |
V |
|
д Z |
д |
|
|
|||||||
|
|
2 |
|
2 |
д |
д |
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
2 |
|
|
|
|
|||||
|
|
Сформулированное |
|
требование не |
является |
обязательным |
и |
решать эту и |
|||||||
|
Yд |
подобные задачи можно и при иной параметризации поверхности |
Д . |
|
|||||||||||
Xд |
|
Почленно складывая первое и третье уравнения, получим, |
что |
Xд Uд Vд . |
|||||||||||
|
Вычтя почленно из первого уравнения третье, |
найдем, что Yд Uд Vд . Подставив |
|||||||||||||
|
|
||||||||||||||
Д
Рис. 1.30. Элементы локальной геометрии поверхности Д , имеющей форму ги-
перболического параболоида.
первое уравнение в четвертое или третье уравнение во второе, придем к результату: Zд UдVд . Следовательно, уравнение гиперболического параболоида Д в
векторной форме может быть записано так:
rд Uд Vд i Uд Vд j UдVдk .
Продифференцировав это уравнение по параметрам U д и Vд , приходим к
следующим зависимостям для:
– направлений касательных прямых
rд |
i j V k; |
rд |
i j U |
д |
k ; |
|
|
||||
Uд |
д |
Vд |
|
|
|
|
|
|
|
– касательной плоскости
|
|
X |
КП |
X M Y |
|
|
Y M |
Z |
КП |
Z |
M |
|
|
|
|
|
|||||||
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
д |
|
|
КП |
д |
|
|
д |
|
|
|
0 ; |
|
|||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
Vд |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
Uд |
|
|
|
|
|
|
|
|
– прямой, нормальной к поверхности Д |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X X |
M |
|
|
Y Y M |
|
Z Z M |
|
||||||||||||
|
|
|
|
|
|
|
д |
|
|
|
|
д |
|
|
|
д |
|
; |
|
|
|
|
|
|
|
|
|
Uд Vд |
|
Uд Vд |
|
2 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
– коэффициентов первой основной квадратичной формы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Eд 2 Vд; |
|
|
Fд UдVд; |
|
|
Gд 2 Uд . |
||||||||||||||||
– коэффициентов второй основной квадратичной формы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Lд 0 ; |
|
|
Mд |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
; |
Nд 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
4 |
2(Uд Vд) UдVд(1 UдVд) |
|
|||||||||||||||||
Главные радиусы кривизны R1.д и R2.д |
поверхности |
Д находятся как корни квадратного уравнения (110) после подстановки в него |
|||||||||||||||||||||
найденных значений коэффициентов Eд , Fд , Gд первой Φ1.д |
|
и Lд , Mд , |
Nд второй Φ2.д |
основных квадратичных форм. |
|||||||||||||||||||
Для анализа строения локального участка сложной поверхности |
Д И будем использовать среднюю |
||||||||||||||
~ |
~ |
|
|
|
~ |
кривизну. По определению эти кривизны равны: |
|||||||||
Mд и , полную (гауссову) |
Gд и и абсолютную |
Aд и |
|||||||||||||
~ |
|
k1.д и k2.д и |
|
|
Eд и |
Nд и 2Fд и Мд и Gд и Lд и |
|
||||||||
Mд и |
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
||||
|
|
|
|
|
|
|
|
|
2[Eд и Gд и Fд и ] |
|
|||||
|
|
~ |
|
|
|
|
|
|
L N |
|
M |
2 |
|
|
|
(1.111) |
|
G |
k |
k |
|
д и д и |
|
|
д и |
; |
|
||||
|
|
|
|
F |
|
|
|||||||||
|
|
д и |
1.д и |
2.д и |
|
E G |
|
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
д и |
д и |
д и |
|
|
||
|
1.3. О классификации рабочих поверхностей деталей и инструментов |
|
|
|
|
|
|
|
|
|
107 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
n д u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
k1.д и |
|
k2.д и |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
C1.д u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ад и |
|
, |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
C2.д u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Д И |
|
|
|
|
|
|
|
|
|
|
где k1.д и и k2.д и – главные кривизны поверхно- |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сти |
|
|
Д И , |
определяемые как корни квадратного |
|||||||||||||||||||
|
|
M |
|
|
t 2 |
|
|
|
|
|
|
|
|
уравнения |
2 |
|
|
|
|
|
|
|
|
|
|
0. |
|
|
||||||||||||
|
l1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
kд и 2Mд и kд и Gд и |
|
|
|||||||||||||||||||||||
Zд u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Нормальная |
|
кривизна |
kд и |
|
поверхности |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
l2 |
|
|
|
|
|
|
|
|
|
|
|
|
Д И представляет собой величину, обратно про- |
|||||||||||||||||||||||
|
rд u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
порциональную радиусу кривизны |
|
Rд и сечения |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
Yд u |
|
|
|
|
|
|
|
|
t1 |
|
|
|
|
поверхности |
|
Д И |
|
плоскостью Cд и , проходя- |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
щей |
через |
|
нормаль |
|
n д и |
к |
|
поверхности: |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kд и Rд и . |
|
|
|
|
|
|
|
|
|
|
|
|
Д И |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Считаем, что |
|
поверхность |
|
задана |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(рис. 1.31) и известна единичная нормаль |
n д и к |
||||||||||||||||||||||
|
|
Xд u |
|
|
|
|
|
|
|
|
|
|
|
|
|
ней в регулярной точке |
M . Единичные векторы |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t i |
|
( i 1, 2, , ) лежат в плоскости, |
касательной |
||||||||||||||||||||||
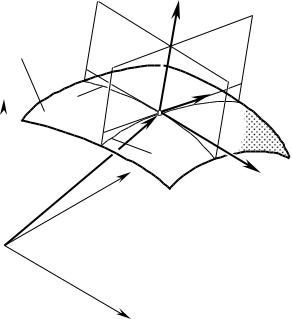
Рис. 1.31. Нормальная кривизна локального участка |
|
к |
Д И |
в точке |
|
M , и представляют различные |
||||||||||||||||||||||||||||||||||
|
направления |
|
на |
|
этой |
|
поверхности. |
Плоскость |
||||||||||||||||||||||||||||||||
|
сложной поверхности |
Д И . |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ci.д и , проходящая через векторы |
n д и |
и |
t i , |
||||||||||||||||||||
пересекает поверхность по плоской кривой li . Нормальная кривизна |
kд и |
|
поверхности |
Д И |
в точке |
M |
||||||||||||||||||||||||||||||||||
равна кривизне соответствующей кривой |
li . |
|
Текущее значение нормальной кривизны рассчитывается по |
|||||||||||||||||||||||||||||||||||||
формуле: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ф2.д и |
|
|
|
L |
|
|
dU |
2 |
|
2М |
д и |
dU |
д и |
dV |
|
N |
д и |
dV2 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
kд и |
|
|
д и |
|
|
д и |
|
|
|
|
д и |
|
|
|
|
д и |
. |
|
|
|
|
|
|
|
(1.112) |
||||||||||||||
|
Ф1.д и |
|
|
E |
д и |
dU 2 |
|
|
2F |
д и |
dU |
д и |
|
dV |
G |
д и |
dV |
2 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
д и |
|
|
|
|
д и |
|
|
|
|
д и |
|
|
|
|
|
|
|
|
|
|
|||||||||||
Если секущую плоскость Cд и |
поворачивать вокруг нормали n д и , то для разных ее положений будем |
|||||||||||||||||||||||||||||||||||||||
иметь свое значение нормальной кривизны ki.д и . Главные кривизны при этом соответствуют наибольшему
k1.д и и наименьшему k2.д и алгебраическому значению нормальной кривизны |
kд и , измеряем в главных |
||||||||
секущих плоскостях C1.д и и C2.д и соответственно. |
|
|
|
|
|
||||
Главные кривизны |
k1.д и и k2.д и находятся как корни квадратного уравнения (109) и измеряются в |
||||||||
нормальных плоскостях, |
касательных к главным направлениям t 1.д и и |
|
t 2.д и |
на поверхности Д И в |
|||||
основании перпендикуляра n д и . Необходимым и достаточным условием того, чтобы направление |
dUд и |
|
|||||||
dVд и |
|||||||||
|
|
|
|
|
|
|
|||
было главным, является равенство нулю определителя: |
|
|
|
|
|
||||
|
Eд и dUд и Fд и dVд и |
Fд и dUд и Gд и dVд и |
|
0 . |
|
(1.113) |
|||
|
|
|
|||||||
|
Lд и dUд и Мд и dVд и |
Мд и dUд и Nд и dVд и |
|
|
|
|
|
||
Существование и единственность соприкасающегося параболоида позволяет классифицировать гладкие регулярные локальные участки поверхности Д И сложной формы исходя из того, определенна, полуопреде-
108 |
1. Рабочие поверхности деталей и инструментов |
ленна или неопределенна его вторая основная квадратичная форма Φ2.д и .
Условие определенности второй основной квадратичной формы Φ2.д и не зависит от вида параметризации поверхности Д И , т.е. от выбора криволинейных координат на ней.
Если вторая основная квадратичная форма Φ2.д и определенна – то такой локальный участок будет
эллиптическим, если полуопределенна – параболическим и если неопределенна – гиперболическим гладким регулярным локальным участком поверхности Д И .
В пределах эллиптического локального участка соприкасающийся параболоид является эллиптическим
параболоидом, аналитический признак которого L |
N |
|
М |
2 |
0, |
а его |
полная (гаусовая) кризизна |
|||
|
~ |
д и д и |
|
д и |
|
Д И |
|
|||
всегда положительна ( |
0 ). Такой локальный участок поверхности |
не пересекает касательную |
||||||||
Gд и |
||||||||||
плоскость, а кривизна |
всех |
нормальных сечений |
имеет |
один |
знак – |
она положительна для выпуклых |
||||
|
|
|
|
|
|
|
|
|
~ |
|
эллиптических локальных участков (в этом случае средняя кривизна поверхности Mд и 0 ) и отрицательна |
||||||||||
|
|
|
|
|
~ |
|
|
|
|
|
для вогнутых эллиптических локальных участков поверхности ( Mд и 0 ). |
|
|||||||||
В частном случае, когда все кривизны становятся |
равными одна другой k1.д и k2.д и kд и , |
|||||||||
эллиптический локальный участок вырождается в омбилический гладкий регулярный локальный участок (локальный участок округления) поверхности Д И . В пределах омбилического локального участка
соприкасающийся эллиптический параболоид вырождается в параболоид вращения. Аналитическим признаком омбилического локального участка поверхности Д И являются соотношения
|
|
|
|
|
|
L N |
д и |
М 2 |
|
0; |
|
Eд и |
|
Fд и |
|
Gд и |
. |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
д и |
|
|
д и |
|
|
Lд и |
|
Мд и |
|
Nд и |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
~ |
Гауссова |
кривизна омбилического |
локального |
участка поверхности Д И |
всегда |
положительна |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
~ |
|
||
( Gд и 0 ), |
а средняя – положительна для выпуклых ( Mд и 0 ) и отрицательна для вогнутых (Mд и 0 ) |
||||||||||||||||||||||||
омбилических локальных участков. |
|
|
|
В пределах омбилического локального участка положе- |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
n д и |
|
С1.д и |
|
ние главных секущих плоскостей C1.д и и C2.д и на поверх- |
||||||||||||||||
Д И |
|
|
|
ности |
Д И становится неопределенным. |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
В пределах параболического локального участка |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
соприкасающийся параболоид вырождается в параболический |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
цилиндр; его аналитический признак L |
N |
M 2 |
0 , а |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
д и |
д и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
гауссова кривизна всегда равна нулю |
( Gд и 0 ). В пределах |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
параболического локального участка поверхность Д И каса- |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Рис. 1.32. Пример параболического локаль- |
ется плоскости по прямой линии, одна из ее главных кривизн |
||||||||||||||||||||||||
равна |
нулю (это |
главное сечение |
имеет точку перегиба |
||||||||||||||||||||||
|
|
ного участка гладкой регулярной |
|||||||||||||||||||||||
|
|
поверхности Д И . |
|
|
|
|
|
(рис. 1.32) или является прямой линией), а другая может быть |
|||||||||||||||||
|
|
|
|
|
|
|
~ |
|
|
|
либо положительной – для выпуклых параболических локаль- |
||||||||||||||
ных участков (в этом случае |
|
|
либо отрицательной – |
для вогнутых параболических локальных |
|||||||||||||||||||||
Mд и 0 ), |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
участков сложной поверхности ( Mд и 0 ). |
|
|
|
|
|
|
|
|
|
|
|
Д И |
|
||||||||||||
|
В частном случае, когда все кривизны параболического локального участка поверхности |
равны |
|||||||||||||||||||||||
нулю k1.д и k2.д и kд и 0 , параболический локальный участок поверхности вырождается в гладкий регулярный локальный участок уплощения. В пределах локального участка уплощения соприкасающийся

1.3. О классификации рабочих поверхностей деталей и инструментов |
|
109 |
||||||||
параболоид вырождается в плоскость, касательную |
к поверхности Д И в рассматриваемой |
ее точке. |
||||||||
Аналитическим признаком локального участка уплощения являются соотношения |
|
|
||||||||
L N |
М 2 |
0; |
L |
М |
д и |
N |
д и |
0. |
|
|
д и д и |
д и |
|
д и |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
~ |
; |
~ |
Гауссова и средняя кривизны локального участка уплощения всегда равны нулю ( Gд и 0 |
Mд и 0 ), |
|||||||||
следовательно нельзя говорить выпуклы они или вогнуты. По этой причине локальные участки уплощения инвариантны относительно стороны расположения тела детали или инструмента: любой из двух возможных вариантов расположения тела детали или инструмента может быть приведен к противоположному путем
поворота поверхности Д И .
Как и для омбилического локального участка, для локального участка уплощения положение главных секущих плоскостей C1.д и и C2.д и на поверхности Д И становится неопределенным.
Все локальные участки на плоскости (регулярные локальные участки уплощения) можно рассматривать как гладкие регулярные локальные участки параболического типа. Локальные участки уплощения можно
также рассматривать и как частный случай омбилических локальных участков поверхностей Д И , когда
нормальная кривизна омбилического локального участка равна нулю. Возможны и иные интерпретации локальных участков уплощения (см. рис. 1.27 – рис. 1.29).
В пределах гиперболического локального участка, соприкасающийся параболоид является гиперболи-
ческим параболоидом. Его аналитический признак L |
N |
д и |
М 2 |
0 . |
|
|
|
|
||||
|
|
д и |
|
д и |
|
|
|
|
|
|
||
Гауссова |
кривизна поверхности |
всегда отрицательная |
~ |
|
|
ее |
средняя |
кривизна |
может |
|||
(Gд и 0 ), а |
||||||||||||
|
~ |
для псевдовыпуклых, |
~ |
|
для |
минимальных |
~ |
|
||||
принимать любые значения (Mд и 0 |
Mд и 0 |
и Mд и 0 для |
||||||||||
псевдовогнутых гладких регулярных локальных участков гиперболического типа поверхностей Д И |
в том |
|||||||||||
числе и при |
фиксированной абсолютной кривизне |
~ |
|
|
|
Главные |
кривизны |
имеют взаимно |
||||
( Aд и Const ). |
||||||||||||
противоположные знаки – следовательно имеются как выпуклые, так и вогнутые нормальные сечения. Поэтому поверхность Д И в пределах гиперболического локального участка выпукловогнута – имеет
седлообразный вид и пересекает касательную плоскость по двум прямым линиям.
Таким образом на гладких регулярных отсеках поверхности Д И встречаются локальные участки
только 10 типов, которые могут быть классифицированы так (рис. 1.33).
Локальный подход к рассмотрению процесса многокоординатного формообразования поверхностей деталей подтверждает правильность использования локального подхода к разработке классификации локальных участков поверхностей деталей и инструментов (см. рис. 1.33) и хорошо согласуется с постулированным выше положением (см. постулат 1.1), в соответствие с которым формообразование сложных поверхностей деталей на многокоординатных станках с ЧПУ следует рассматривать в первую очередь локально: в окрестности текущей точки касания поверхностей Д и И .
Анализ топологии гладких регулярных локальных участков поверхности Д И включает определение
соотношений нормальных кривизн поверхности в дифференциальной окрестности текущей точки на ней. Структуру нормальных кривизн в заданной точке на поверхности Д И удобно графически изображать
при помощи характеристической кривой – индикатрисы кривизны, которая дает наглядное представление о распределении нормальных радиусов кривизны в окрестности точки на поверхности Д И . В геометрии для
этих целей используется индикатриса Дюпена1 – плоская характеристическая кривая второго порядка, которая
1Дюпен, Франсуа Пьер-Шарль (Dupin, F.P.-C.). (6.10.1784, Варзи, Ниверне - 18.1.1873, Париж), французский геометр и экономист, чл. Парижской АН (1818), почетный член Петербургской АН (с 1828). Окончил Политехническую школу в Париже (1804). Был морским инженером, затем – главным инженером французского флота, с 1819 – профессор Консерватории искусств и ремесел, с 1834 –морской министр. Труды в области дифференциальной геометрии – поверхности ортогональной системы пересекаются вдоль общих линий кривизны (теорема Дюпена). Развивая идеи своего учителя Г.Монжа, ввел кривую, позволяющую наглядно представить распределение кривизн поверхности в различных нормальных ее сечениях (индикатриса Дюпена). Как экономист выступал сторонником протекционизма.
