
Radzevich, S.P. Monograph - 2001
.pdf
30 |
1. Рабочие поверхности деталей и инструментов |
|
Нормаль к поверхности Д(И). В теории формообразования поверхностей при механической обработке деталей принято, что нормаль к поверхности Д И в каждой точке поверхности направлена от тела детали
или от исходного инструментального тела (ИИТ), т.е. от тела, ограниченного исходной инструментальной поверхностью. Это следует иметь в виду при выборе направлений осей локальной системы координат с тем, чтобы обеспечить правильное направление нормали.
Нормаль к поверхности Д И в текущей точке M ее гладкого регулярного участка – это вектор Nд и ,
проходящий через точку M перпендикулярно к касательной плоскости в этой же точке (см. рис. 1.5). Вектор нормали Nд и рассчитывается по уравнению:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Xд и |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vд и |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N X.д и |
||||
|
rд и |
T |
|
rд и |
|
Xд и |
|
Yд и |
|
Zд и |
|
|
Yд и |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
NY.д и |
|
||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
Nд и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
Vд и |
|
|
N |
|
. |
|
U |
|
|
V |
U |
д и |
|
U |
д и |
|
U |
д и |
Z.д и |
|||||||||||||
|
|
д и |
|
|
д и |
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vд и |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Д И |
Nд u |
rд u |
Касательная |
|
Vд u |
|
|
|
плоскость |
|
Vд и линия |
|
|
Zд u |
rд u |
|
rд u |
||
Uд u |
||
|
Uд и линия |
|
|
Yд u |
Это выражение преобразуется к виду
Nд и N X.д и |
NY.д и |
NZ.д и |
1 Т |
Yд и
U д и
Zд и
U д и
Xд и
U д и
Zд и Yд и
Vд и Vд и
Xд и Zд и
Vд и Vд и
Yд и Xд и
Vд и Vд и
1
Zд и
U д и
Xд и
U д и .
Yд и
U д и
|
|
Xд u |
|
|
|
|
|
|
|
|
|
|
Орт нормали к поверхности |
Д И равен: |
||||||||||||||
Рис. 1.5. Касательная плоскость к поверхности Д И |
|
|
|
|
|
n д и |
|
Nд и |
. |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
сложной формы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mod N |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
|
|||
Первая основная |
квадратичная форма поверхности Д(И) |
по |
определению |
есть |
|
квадрат линейного |
||||||||||||||||||||||
элемента этой поверхности в направлении, определенном относительно нее соотношением |
|
dVд и |
дифферен- |
|||||||||||||||||||||||||
|
dUд и |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
циалов. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть l t r U д и t , Vд и t |
– регулярная кривая на поверхности Д И . Тогда квадрат дифферен- |
|||||||||||||||||||||||||||
циала длины дуги этой кривой равен (Elber, G., Cohen, E., 1993): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
dsд и 2 |
dUд и |
|
dVд и |
ˆ |
dUд и |
|
dVд и T |
dUд и |
|
dVд и |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Φ1.д и |
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
dt |
|
|
dt |
|
G д и |
dt |
|
dt |
|
|
dt |
|
|
|
dt |
. |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||

|
|
|
1.2. Задание рабочих поверхностей деталей и инструментов. |
|
31 |
|||||||||||||||||||||||||||||||||
|
|
|
|
Расчет элементов их локальной геометрии |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Функция Φ1.д и |
известна как первая основная квадратичная форма поверхности |
Д И с матрицей |
||||||||||||||||||||||||||||||||||||
Gˆ д и , равной: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rд и |
|
|
|
rд и |
|
|
|
rд и |
|
|
|
|
rд и |
|
|
|||||||||||||
|
|
Gˆ д и |
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
||
|
|
gij |
|
|
|
U |
|
|
|
U |
|
|
|
|
|
|
U |
|
|
|
V |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
д и |
|
|
|
|
|
д и |
|
|
|
|
д и |
|
|
|
д и |
. |
|
|||||||||||||||
|
|
|
|
|
д и |
|
|
|
rд и |
|
, |
|
rд и |
|
|
|
|
rд и |
, |
|
|
rд и |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
V |
|
|
U |
д и |
|
|
|
|
V |
|
|
V |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
д и |
|
|
|
|
|
|
|
д и |
|
|
|
|
|
д и |
|
|
||||||||||||
Здесь скобки , обозначают внутреннее произведение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Уравнение первой основной квадратичной формы Φ1.д и |
поверхности |
Д И может быть записано в |
||||||||||||||||||||||||||||||||||||
виде: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ф |
|
|
ds |
2 |
E |
|
|
dU 2 |
|
2F |
|
|
dU |
|
dV |
|
|
G |
|
dV 2 |
(1.4) |
|||||||||||||||||
1.д и |
|
|
д и |
|
д и |
|
д и |
|
|
|
|
|
д и |
|
|
|
д и |
|
д и |
|
|
|
|
|
д и |
д и |
|
|||||||||||
и представимо в матричной форме: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Ф |
|
|
mod 2 dr |
|
dU |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dU |
|
|
|
|
|||||||||||||
|
|
д и |
д и |
|
|
dV |
|
|
|
|
|
д и , |
(1.5) |
|||||||||||||||||||||||||
|
1.д и |
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
|
|
д и |
|
|
|
|
dV |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
|
||||
где симметричная матрица
|
|
|
|
|
|
rд и |
|
|
rд и |
||||||
|
E |
|
F |
|
|
|
|
|
|
|
|
|
|
||
д и |
д и |
U |
д и |
U |
д и |
||||||||||
|
|||||||||||||||
|
|
|
|
|
|
|
|
||||||||
д и |
Fд и |
Gд и |
|
rд и |
|
|
rд и |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
Uд и |
|
Vд и |
|||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rд и
Uд иrд и
Vд и
|
|
rд и |
|
|
rд и |
|
|
||||
|
|
|
|
|
|
|
|
|
|
rд и |
|
|
|
|
|
|
|
||||||
|
|
Vд и |
|
U д и |
|||||||
|
|
|
|||||||||
|
|
U д и |
|||||||||
|
rд и |
|
|
rд и |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Vд и |
|
|
Vд и |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
rд и
(1.6)
Vд и
является первой основной фундаментальной матрицей или метрическим тензором поверхности Д И .
Коэффициенты первой основной квадратичной формы (первой основной дифференциальной формы Гаусса1) определяются по формулам:
|
2 |
|
rд и |
|
rд и |
|
rд и |
|
2 |
|
rд и |
||||
Eд и mod |
|
|
|
; |
Fд и mod |
|
|
mod |
|
; |
Gд и mod |
|
|
|
. |
|
|
|
|
|
|
||||||||||
|
|
|
U д и |
|
U д и |
|
Vд и |
|
|
|
Vд и |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1Гаусс, Карл Фридрих (Gauss , Karl Friedrich ) (30.4.1777, Брауншвейг, – 23.2.1855, Гёттинген), немецкий математик, внесший фундаментальный вклад также в астрономию и в геодезию. Родился в семье водопроводчика. В 1794-95 открыл и в 1821-23 разработал основной математический метод обработки неравноценных наблюдательных данных (метод наименьших квадратов). Его геометрические исследования связаны с практикой геодезии. Изучение формы земной поверхности потребовало углубленного общего геометрического метода для исследования поверхностей. Выдвинутые Гауссом в этой области идеи получили выражение в сочинении “Общие изыскания о кривых поверхностях” (1828) [Gauss, K.-F., Disquisitions Generales Circa Superficies Curvas, Gottingen, 1828. (English translation: General
Investigation of Curved Surfaces, by J.C.Morehead & A.M.Hiltebeitel, Princeton, 1902; reprinted with introduction by Courant, Raven Press, Hewlett, New York, 1965, 119p.).]. Руководящая мысль этого сочинения состоит в том, что при изучении поверхности как бесконечно тонкой гибкой пленки основное значение имеет не уравнение поверхности в декартовых координатах, а дифференциальная квадратичная форма, через которую выражается квадрат элемента длины и инвариантами которой являются все собственные свойства поверхности – прежде всего ее кривизна в каждой точке. Другими словами, Гаусс предложил рассматривать те свойства поверхности (т.н. внутренние), которые не зависят от изгибаний поверхности, не изменяющих длин линий на ней. Созданная таким образом внутренняя геометрия поверхностей в дальнейшем послужила образцом для создания n-мерной римановой геометрии.

32 |
1. Рабочие поверхности деталей и инструментов |
|
Очевидно, что коэффициенты Eд и и Gд и всегда положительны ( Eд и 0 , Gд и 0 ), а коэффициент Fд и может принимать и нулевое значение Fд и 0 . Поэтому первая основная квадратичная форма поверхности Д И является положительно определенной – она принимает только неотрицательные значения ( Φ1.д и 0 ), а в нуль обращается только в случае, когда U д и Vд и 0 . Это очевидно также из того, что
квадратный корень из первой основной квадратичной формы представляет собой дифференциал дуги кривой на поверхности Д И , длина которого может принимать только неотрицательные значения.
Приведенные соотношения для определения первой основной квадратичной формы поверхности Д И и ее гауссовых коэффициентов Eд и , Fд и и Gд и чрезвычайно полезны при решении задачи синтеза
наивыгоднейшего формообразования поверхности детали на металлорежущем станке.
Если две поверхности Д и И имеют одинаковые первые основные квадратичные формы, т.е. Φ1.д Φ1.и , то одну из них можно наложить на другую. Для этого достаточно, чтобы выполнялись соотношения Eд Eи, Fд Fи и Gд Gи (Норден, А.П., 1948, с. 174-175) – иными словами, наложимые одна на другую поверхности Д и И допускают такую параметризацию, при которой в точках этих
поверхностей с одинаковыми криволинейными координатами соответствующие коэффициенты их первых основных квадратичных форм равны. Примерами поверхностей, разворачивающихся одна на другую, служат цилиндр и плоскость, катеноид и геликоид и др.
Свойство поверхностей Д и И быть наложенными одна на другую имеет важные технологические
приложения. Вопрос о разворачиваемости одной поверхности на другую важен при решении задачи профилирования фасонных прижимных кулаков для ленточного шлифования сложных поверхностей деталей, например, для шлифования рабочих поверхностей турбинных лопаток и т.п. деталей. Поскольку шлифовальная лента изготавливается из тканного материала и может быть развернута на плоскость, то и фасонная рабочая поверхность прижимного кулака должна быть разворачивающейся на плоскость. Для этого достаточно, чтобы в каждой точке поверхности И прижимного кулака выполнялось условие

 EиGи Fи2 0 . В противном случае абразивная лента неизбежно будет растягиваться неравномерно и,
EиGи Fи2 0 . В противном случае абразивная лента неизбежно будет растягиваться неравномерно и,
вследствие этого, рваться. При невыполнении условия |
Eд Eи, Fд Fи и Gд Gи |
допустимы только |
упругие ее деформации. |
Д И просто получаются |
|
Вторые производные уравнения поверхности |
путем повторного |
дифференцирования соответствующих уравнений (2) и (3) для первых производных:
|
|
|
|
|
2 Xд и |
U , V |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
д и |
||
|
|
|
|
|
|
U |
2 |
|
|
|||||
|
|
|
|
|
|
|
д и |
|
|
|
|
|||
2r |
|
|
|
|
2Y |
|
|
|
|
|||||
|
|
д и |
|
|
|
|
д и |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
2 |
|
|
|
|
2 |
|
U д и , Vд и ; |
|||||
U |
|
|
|
U |
|
|
|
|
|
|||||
|
д и |
|
|
д и |
|
|
|
|||||||
|
|
|
|
|
|
2 Z |
|
|
|
|
|
|
||
|
|
|
|
|
|
д и |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
U |
, V |
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
U |
2 |
|
|
д и |
д и |
|
|||
|
|
|
|
|
|
|
|
д и |
|
|
|
|
||
|
|
|
|
|
2 Xд и |
U |
, V |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
д и |
||
|
|
|
|
|
|
V 2 |
|
||||||
|
|
|
|
|
|
|
д и |
|
|
|
|
||
2r |
|
|
|
|
2Y |
U |
|
|
|
||||
|
|
д и |
|
|
|
д и |
, V |
|
|||||
|
|
|
|
|
|
|
|
||||||
|
V |
2 |
|
|
|
|
V 2 |
|
д и |
д и |
|
||
|
д и |
|
|
|
д и |
|
|
|
|
||||
|
|
|
|
|
2 Z |
|
|
|
|
|
|||
|
|
|
|
|
|
д и |
|
|
|
|
|||
|
|
|
|
|
|
|
|
U |
, V |
|
|||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
V 2 |
|
д и |
д и |
|
||||
|
|
|
|
|
|
|
д и |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
2 Xд и |
U |
, V |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д и д и |
|
|
|
|
|
|
|
|
|
U |
|
|
V |
|
|
|||
|
|
2 |
|
|
|
|
|
|
д и |
д и |
|
|
|
|||
|
rд и |
|
|
|
2 |
Yд и |
U |
|
. |
|||||||
|
|
|
|
|
|
, V |
||||||||||
|
|
|
V |
|
U |
|
|
V |
||||||||
U |
|
|
|
|
|
|
|
д и д и |
|
|||||||
|
д и |
д и |
|
|
|
д и |
д и |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
2 |
Zд и |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
U |
, V |
|
||||
|
|
|
|
|
|
|
|
U |
|
|
V |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
д и д и |
|
|||
|
|
|
|
|
|
|
|
|
д и |
д и |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
|
1.2. Задание рабочих поверхностей деталей и инструментов. |
|
|
33 |
||||||
|
|
|
Расчет элементов их локальной геометрии |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
Вторая основная квадратичная форма поверхности Д(И) по определению есть проекция на направление |
|||||||||||
нормали |
n д и |
перемещения конца бесконечно малого вектора касательной |
drд и . |
|
|||||||
Рассматривая все кривые l t |
, проходящие через точку M U M , V M |
, и дифференцируя их уравнения |
|||||||||
|
|
|
|
д и |
д и |
|
|
|
|
||
дважды, |
для поверхности Д И |
в точке M U M |
, V M можно выделить свойства второго порядка. Вторые |
||||||||
|
|
|
д и |
д и |
|
|
|
|
|
|
|
|
|
|
|
|
r |
д и |
|
|
r |
д и |
|
производные от |
l t в качестве факторов содержат выражения с |
|
|
и |
|
. Однако внутреннее |
|||||
|
|
|
|
||||||||
|
|
|
|
|
U д и |
|
Vд и |
||||
|
|
|
|
|
|
|
|
|
|
|
|
произведение этих выражений на |
|
n д и |
|
всегда равно нулю, поскольку частные производные расположены в |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
плоскости, |
|
касательной к поверхности |
|
Д И . |
Поэтому в |
n |
|
|
|
|
U |
|
|
|
|
, V |
|
|
, |
d 2l t |
|
|
компонента |
|
d 2l t |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dt2 |
|
|
|
|
dt 2 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
|
|
д и |
|
|
д и |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
направлена перпендикулярно к поверхности Д И и состоит только из вторых производных: |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
n д и U д и , Vд и , |
d 2 l t |
|
|
n д и U д и , Vд и , |
d 2 rд и |
|
dU |
д и 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
dt |
2 |
|
|
|
|
|
dU |
2 |
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
d |
2 r |
д и |
|
|
|
|
dU |
д и |
|
|
|
dV |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d 2 r |
д и |
dV |
|
2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
|
|
|
|
||||||||||||
2 n д и U д и , Vд и , |
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
dt |
|
|
|
|
|
n д и U д и , Vд и , |
|
|
|
2 |
|
|
|
|
dt |
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
dU д и dVд и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dVд и |
|
|
|
|
|
|
|
||||||||||||||||||||
dU |
д и |
|
dV |
|
|
|
|
dU |
д и |
|
dV |
|
T |
|
|
|
|
|
|
|
dU |
д и |
|
|
|
dV |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
д и |
Lˆ |
д и |
|
|
|
|
|
|
д и |
|
Φ2.д и |
|
|
|
, |
|
|
|
|
|
д и |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
dt |
|
|
dt |
|
|
dt |
|
|
|
dt |
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Функция Φ2.д и |
известна как вторая основная квадратичная форма поверхности |
|
Д И . |
Ее матрица |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Lˆ д и записывается так: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
rд и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
rд и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
, |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
д и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
Lˆд и lij д и |
|
|
|
|
|
|
|
|
|
Uд и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
|
д и |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
rд и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
rд и |
|
|
|
. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
д и |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
д и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vд и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение второй основной квадратичной формы Φ2.д и поверхности |
|
Д И преобразуется к виду: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Ф |
2.д и |
|
dr |
д и |
dn |
д и |
L |
|
|
dU 2 |
|
2M |
д и |
dU |
д и |
dV |
|
N |
д и |
dV 2 . |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
|
|
|
д и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
|
|
|
|
|
|
д и |
|
|
|
|
|
|
||||||||||||||||||||||||||
По аналогии с (5) для второй основной квадратичной формы Φ2.д и |
можно записать ее матричное |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
представление: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Ф |
|
|
|
|
|
dU |
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
dU |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
2.д и |
|
dV |
|
|
|
д и |
N |
д и |
|
|
|
|
|
д и . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
|
|
д и |
|
|
M |
д и |
д и |
dV |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Симметричная матрица

34 |
1. Рабочие поверхности деталей и инструментов |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2rд и |
|
|
|
2rд и |
|
|||||||||||
|
|
|
n д и |
|
|
|
|
|
|
|
|
n д и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
U |
|
|
|
V |
|
U |
|
|
||||||||||
|
|
|
|
|
|
д и |
|
|
д и |
|
|||||||||||
Lд и |
Mд и |
|
|
|
|
|
|
|
|
|
|
д и |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Mд и |
Nд и |
|
|
|
|
2 |
rд и |
|
|
|
|
2 |
rд и |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
n д и |
|
|
|
|
|
|
n д и |
|
|
|
|
|
|
|
|||||
|
|
U |
д и |
V |
|
|
2 |
|
|
||||||||||||
|
|
|
|
|
|
|
д и |
|
|
|
Vд и |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
является вторым фундаментальным тензором поверхности |
Д И . Ее |
определитель (т.н. определитель |
|||||||||||||||||||
Грама) равен полной (гауссовой) кривизне этой поверхности:
|
|
|
|
|
|
|
|
Lд и |
Mд и |
|
|
|
~ |
||
|
|
|
|
|
|
|
|
Mд и |
Nд и |
|
k1.д и k2.д и Gд и . |
||||
Элементы |
bij |
являются |
компонентами тензора кривизны |
в естественных координатах det bij |
|||||||||||
k |
k |
2.д и |
det g |
ij |
k |
k |
2.д и |
|
Eд и |
Fд и |
|
. |
|
||
|
|
|
|||||||||||||
1.д и |
|
|
1.д и |
|
|
Fд и |
Gд и |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Вторую основную квадратичную форму Ф2.д и называют также оператором формы или отображением
Вейнгартена1 (Koenderink, J.J., 1990, c. 211).
Коэффициенты Eд и , Fд и , Gд и первой Φ1.д и и Lд и , Mд и , Nд и второй Φ2.д и основных
квадратичных форм (основных дифференциальных форм Гаусса) играют исключительно важную роль в дифференциальной геометрии поверхностей, в инженерной геометрии и в теории формообразования поверхностей при механической обработке деталей. Они введены К.-Ф. Гауссом и носят название гауссовых коэффициентов соответственно первого (в них входят производные только первого порядка) и второго порядка (определяемые производными первого и второго порядка).
1.2.2.2. Векторная форма. В инженерной геометрии широкое применение находит векторная алгебра. Использование компактной векторной формы аналитического описания поверхности Д И позволяет
наглядно интерпретировать задачи формообразования поверхностей деталей геометрически. Решая задачи синтеза наивыгоднейшего формообразования, часто приходится рассматривать векторное описание поверх-
ностей Д И совместно с матричным преобразованием координат.
Отличие вектора от столбцовой матрицы большей частью состоит в форме их записи, а использование той или иной формы записи определяется тем, в какое выражение – векторное или матричное они входят2.
Чтобы к векторам можно было применять аппарат матричного исчисления, их записывают как матрицыстолбцы, составленные из координат векторов в выбранном базисе.
Уравнение поверхностей деталей и инструментов. На координаты Xд и , Yд и , Zд и текущей точки на
поверхности |
Д И можно смотреть как на компоненты ее радиус-вектора rд и . Поэтому уравнение: |
|
(1.7) |
rд и rд и U д и , Vд и , |
U д и , Vд и G, |
показывает, что радиус-вектор rд и текущей точки M поверхности Д И представляет собой функцию двух независимых переменных U д и и Vд и .
В развернутом виде уравнение (7) записывается так:
1Вейнгартен, или Вайнгартен, Юлиус (Weingarten , J.) (25.3.1836 – 16.6.1910) – немецкий математик. Родился в Берлине. Профессор политехникума в Фрейбурге. Основные труды относятся к дифференциальной геометрии. Известны так называемые деривационные формулы, поверхность, функция, теорема, носящие имя Вейнгартена.
2При этом не следует забывать и об отличиях. Например, для векторов определено как векторное, так и скалярное произведение, чего нет для матриц.

1.2. Задание рабочих поверхностей деталей и инструментов. |
|
35 |
Расчет элементов их локальной геометрии |
|
|
|
|
|
rд и Xд и U д и , Vд и iд и Yд и Uд и , Vд и jд и Zд и Uд и , Vд и |
k д и . |
(1.8) |
Поверхность Д И будет задана, если задана векторная функция (7). При этом, фиксируя один из параметров Uд и или Vд и , имеем один переменный параметр и, следовательно, векторные уравнения
|
|
|
|
|
|
|
r |
д и |
r |
д и |
U M ;V |
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
r |
д и |
r |
д и |
U |
|
|
, V |
M |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
д и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
д и |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
описывают лежащие на поверхности |
Д И |
параметрические кривые. Очевидно, что U M и |
V |
M являются |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
|
д и |
|
|
|
|
||
константами из множества значений Uд и |
|
и |
Vд и . |
Если варьировать величинами констант, |
поверхность |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Д И |
покроется непрерывной сетью параметрических |
|
кривых, формируя при этом семейство кривых |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Uд и Const |
и трансверсальное ему семейство кривых Vд и Const . Через каждую обыкновенную точку на |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
поверхности |
Д И проходит по одной координатной кривой из каждого семейства. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Угол д и между параметрическими Uд и |
и Vд и |
|
кривыми рассчитывается по одной из следующих |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
формул: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
Fд и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
G |
д и |
F |
|
2 |
|
|
|
|
|
|
|
|
Hд и |
|
|
|
|
|
|
Hд и |
|
|
|
|
|
|||||||||||||||
|
|
cos д и |
|
|
|
|
; |
|
|
sin д и |
|
|
|
|
д и |
|
|
д и |
|
|
|
|
|
|
|
; |
|
tan д и |
. |
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fд и |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Eд и Gд и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Eд и Gд и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Eд и Gд и |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
Первые производные уравнения поверхности |
|
|
|
Д И |
при задании их векторным уравнением записыва- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ются в виде: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
rд и |
|
|
|
Xд и |
i |
д и |
|
|
|
Yд и |
j |
д и |
|
|
Zд и |
k |
|
|
; |
|
|
|
|
|
|
|
|
|
|
(1.9) |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Uд и |
|
|
|
|
Uд и |
Uд и |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Uд и |
|
|
|
|
|
|
|
|
|
|
д и |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
rд и |
|
|
Xд и |
i |
д и |
|
Yд и |
j |
д и |
|
|
Zд и |
k |
|
. |
|
|
|
|
|
|
|
|
|
|
|
(1.10) |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
V |
|
|
|
|
|
|
V |
|
|
|
|
д и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
|
|
|
|
|
д и |
|
|
|
|
|
|
|
|
|
|
|
|
д и |
|
|
|
|
|
|
|
|
|
д и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Первые производные уравнений (9) и (10) поверхности |
|
Д И |
по каждому из |
Uд и , Vд и |
параметров |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
определяют векторы |
|
rд и |
|
и |
rд и |
, касательные к координатным линиям. Векторы касательных |
|
|
rд и |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Uд и |
Vд и |
|
Uд и |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
и |
rд и |
|
не обязательно взаимно ортогональны и в общем случае не единичны. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
Vд и |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д И уравнением в векторной форме касатель- |
||||||||||||||||||||||||||||
|
Касательная плоскость. В случае описания поверхности |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ная плоскость определяется так |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
КП r |
M |
|
|
rд и |
|
|
rд и |
|
0 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.11) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
д и |
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
где rКП – радиус-вектор текущей точки касательной плоскости. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Нормаль к поверхности |
Д И в текущей точке M ее гладкого регулярного участка – это вектор |
Nд и , |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
проходящий через точку M перпендикулярно к касательной плоскости в этой же точке (см. рис. 1.5). Вектор
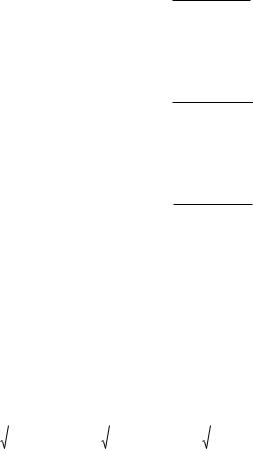
36 |
|
|
|
|
|
|
|
|
1. Рабочие поверхности деталей и инструментов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нормали Nд и к поверхности |
Д И рассчитывается по формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
r |
д и |
|
r |
д и |
|
|
Y , Z |
д и |
|
|
|
|
|
|
Z |
|
|
|
|
, X |
д и |
|
|
|
X |
|
|
|
,Y |
|
|
|
J |
|
|
|
|
|
. |
||||||||||||||||||||||||
(1.12) |
N |
|
|
|
|
|
|
д и |
|
|
|
|
|
|
|
|
|
|
д и |
|
|
|
|
|
|
|
|
д и |
д и |
|
|
J |
|
J |
|
||||||||||||||||||||||||||||||||
д и |
|
|
|
|
|
|
U |
|
|
,V |
|
|
|
|
|
U |
|
|
|
|
,V |
|
|
|
|
|
|
|
|
U |
|
|
|
,V |
|
|
x |
y |
z |
||||||||||||||||||||||||||||
|
|
|
U |
д и |
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
д и |
|
д и |
|
|
д и |
|
|
|
|
|
|
|
|
|
д и |
|
|
д и |
|
|
|
|
|
|
|
|
д и |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь якобианы J x, J y, J z соответственно равны: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Yд и |
|
|
|
Zд и |
|
|
|
|
|
Yд и , Zд и |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
J x |
Uд и |
|
|
Uд и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
(1.13) |
|
|
|
|
|
|
|
|
|
|
|
|
|
Yд и |
|
|
Zд и |
|
|
|
U |
|
|
|
|
|
, V |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
д и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vд и |
|
|
|
Vд и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Zд и |
|
|
Xд и |
|
|
|
|
Z |
|
|
|
|
|
|
, X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
д и |
|
U |
д и |
|
|
|
|
|
|
|
|
|
|
|
д и |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
J y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
(1.14) |
|
|
|
|
|
|
|
|
|
|
|
|
Zд и |
|
Xд и |
|
|
|
U |
|
|
|
|
|
|
, V |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
д и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vд и |
|
|
Vд и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Xд и |
|
|
|
|
Yд и |
|
|
|
|
|
Xд и , Yд и |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
J z |
Uд и |
|
|
Uд и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
(1.15) |
|
|
|
|
|
|
|
|
|
|
|
|
Xд и |
|
|
|
Yд и |
|
|
|
|
U |
|
|
|
|
|
|
, V |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
д и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vд и |
|
|
|
Vд и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Орт нормали n д и рассчитывается по формуле: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rд и |
|
|
|
|
r |
д и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n д и |
|
Nд и |
|
|
|
|
|
Uд и |
|
Vд и |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Nд и |
|
|
|
|
rд и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
д и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Uд и |
|
Vд и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
или, с учетом (12): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
J x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J z |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
n д и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
J y2 |
J z2 |
|
|
|
|
J x2 J y2 J z2 |
|
|
|
|
|
|
|
|
J x2 |
J y2 |
J z2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
J x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Зависимости (9) и (10) позволяют так записать уравнение прямой, направляющим вектором которой служит нормаль к поверхности Д И :
|
n |
|
|
r |
д и |
|
r |
д и |
|
|
|
r |
rд и |
|
|
|
|
|
, |
||||
|
|
U |
д и |
V |
|
||||||
|
|
|
|
|
|
|
|
д и |
|
||
где – число, определяющее положение текущей точки на прямой.
Нормаль к поверхности Д И и ее первые производные компактно записываются так (Maekawa, T., and Patrikalakis, N., 1994):
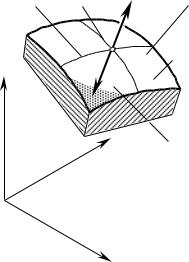
1.2. Задание рабочих поверхностей деталей и инструментов. |
37 |
||||||||||||||||||||||||||||||
|
|
Расчет элементов их локальной геометрии |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
Nд и |
|
rд и |
|
|
rд и |
; |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
U |
д и |
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
|
|
|
|
|
|
|
|
|
|
||||||
|
Nд и |
|
|
2rд и |
|
rд и |
|
|
|
rд и |
|
2rд и |
|
; |
|
||||||||||||||||
|
U |
д и |
|
|
2 |
V |
|
|
U |
д и |
U |
|
|
|
V |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
Uд и |
|
|
д и |
|
|
|
|
|
|
|
д и |
д и |
|
|
|
||||||||||||
Nд и |
|
|
|
2rд и |
|
|
|
rд и |
|
rд и |
|
|
2rд и |
|
. |
||||||||||||||||
V |
|
|
U |
V |
|
|
|
V |
|
|
|
U |
д и |
|
2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
д и |
|
|
|
д и |
д и |
|
|
д и |
|
|
|
|
|
Vд и |
|
|
|
|||||||||||||
В геометрическом аспекте поверхность имеет две стороны. Практически же она всегда принадлежит детали или инструменту, носителям формы этой поверхности. Это приводит к тому, что в машиностроении различают открытую и закрытую стороны поверхности детали (рис. 1.6) и инструмента. Сторона поверхно-
сти Д И , примыкающая к материалу детали или
инструмента, является закрытой, а противоположная, свободная для контакта с другими предметами, – открытой.
В теории формообразования поверхностей при механической обработке деталей принято, что
в каждой точке нормаль к поверхности Д И про-
ведена с открытой ее стороны, т.е. направлена от тела детали и от исходного инструментального тела. Это следует иметь в виду при выборе направлений осей локальной системы координат или порядка сомножителей в формуле (12) с тем, чтобы векторное произведение касательных к поверх-
ности Д И обеспечивало правильное направление нормали к ней.
U д линия |
Vд линия |
Д |
|
|
nд |
|
M |
открытаясторона |
|
поверхности Д |
|
|
|
|
Zд |
д |
|
|
|
|
|
Yд |
закрытаясторона |
|
поверхности Д |
Пример 1.1. Рассмотрим порядок определения вектора |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Xд |
|||||||||||||||||||||
нормали Nи к исходной инструментальной поверхности кони- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
ческой фрезы (рис. 1.7) с углом при вершине |
|
45 |
|
в текущей |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
точке M на ее исходной инструментальной поверхности И . |
|
|
|
|
Рис. 1.6. Открытая и закрытая стороны поверхности |
||||||||||||||||||||||||||||||||||
Пусть поверхность И параметризована так: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
детали Д . |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
rи iиUи sin и sin Vи jиUи sin и cosVи k иUи cos и. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Тогда: |
|
|
|
rи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
i |
и |
sin |
и |
sin V j |
и |
sin |
и |
cosV k |
и |
cos |
и |
; |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
Uи |
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
rи |
|
i |
и |
U |
и |
sin |
и |
cosV j |
и |
U |
и |
|
sin |
и |
sinV . |
|
|
|
|
||||||||||||||||
|
|
|
|
Vи |
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Следовательно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rи |
|
|
|
rи |
|
|
|
|
|
|
|
iи |
|
|
|
|
|
|
|
|
|
|
|
jи |
|
|
|
|
k и |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
N |
|
|
|
|
|
|
U |
|
sin |
|
cosV |
|
|
|
U |
|
sin |
|
sinV |
|
0 |
|
|
||||||||||||||||
|
и |
|
V |
|
U |
и |
|
|
|
|
|
и |
|
|
и |
|
|
|
и |
|
|
|
|
|
и |
|
|
и |
|
и |
|
|
|
|
|||||
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
sin и |
sinVи |
|
|
|
|
|
sin и cosVи |
|
cos и |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
= iиUи sin и cos и sinVи jиUи cos и k иUи sin 2 и .
Исходя из этого просто находится орт нормали.
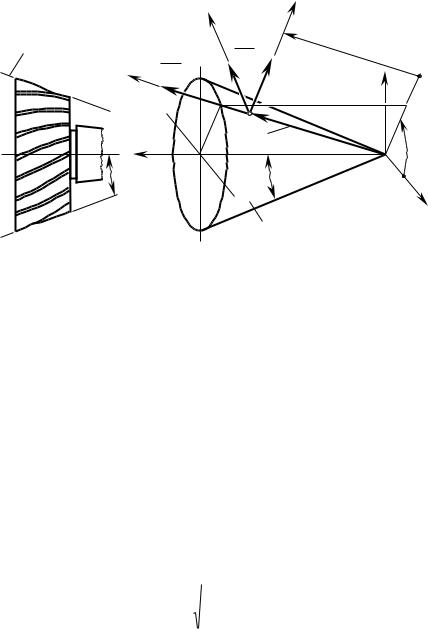
38 |
1. Рабочие поверхности деталей и инструментов |
|
|||
|
|
|
|
|
|
|
|
|
|
z M |
|
|
|
|
y M |
u |
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
И |
ru |
|
ru |
U u |
|
|
Vu |
|
||
|
M |
|
|
||
|
xu |
Uu |
|
Nu |
|
|
|
|
Xu |
||
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
Zu |
|
ru |
Vu |
|
|
|
|
|
|
|
u |
|
|
u |
|
|
|
|
|
|
Yu |
|
|
|
|
И |
|
|
Рис. 1.7. Построение нормали к конической поверхности И инструмента. |
||||
Вектор нормали Nи к поверхности И и векторы касательных |
rи |
, |
rи |
к координатным кривым на |
Uи |
|
|||
|
|
Vи |
||
ней используются в качестве направляющих векторов локальной системы координат (подвижного репера) с началом в текущей точке M на поверхности И .
Создающие базис орты этой системы будут:
|
|
|
|
rи |
|
|
|
|
|
|
|
rи |
|
|
|
|
|
|
|
|
rи |
|
rи |
|
|
|||||
(1.16) |
i |
M |
|
Uи |
|
; |
j |
M |
Vи |
; |
|
|
k |
M |
|
Uи |
Vи |
. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
и |
rи |
|
|
|
и |
|
rи |
|
|
|
|
и |
rи |
|
rи |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
Uи |
|
|
|
|
|
|
|
Vи |
|
|
|
|
|
|
|
|
Uи |
Vи |
|
|||||||
Орт k иM n и |
локальной системы координат на поверхности |
|
|
Д И равен |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
rи |
|
rи |
|
|
|
|
|
|
|
|
|
|
|||||||
(1.17) |
|
|
|
|
|
|
n и |
|
|
|
Uи |
Vи |
|
|
|
. |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
r |
и |
|
|
|
r |
и |
|
2 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
U |
и |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|||
Направляющие косинусы вектора нормали рассчитываются по формулам:
|
|
|
Yи |
|
|
Zи |
|
|
|
|
|
|
Zи |
|
Xи |
|
|
|
|
|
|
Xи |
|
|
|
Yи |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
Uи |
|
|
Uи |
|
|
|
|
|
|
Uи |
|
Uи |
|
|
|
|
|
|
Uи |
|
|
Uи |
|
|
|
||||
|
|
|
Yи |
|
|
Zи |
|
|
|
|
|
|
|
Zи |
|
Xи |
|
|
|
|
|
|
Xи |
|
|
|
Yи |
|
|
|
|
cos |
|
|
Vи |
|
|
Vи |
|
|
; |
cos |
|
|
Vи |
|
Vи |
|
|
; |
cos |
|
|
Vи |
|
|
|
Vи |
|
|
, |
||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
Nи |
|
|
|
|
Nи |
|
|
|
|
Nи |
|||||||||||||||||
где нормирующий множитель равен
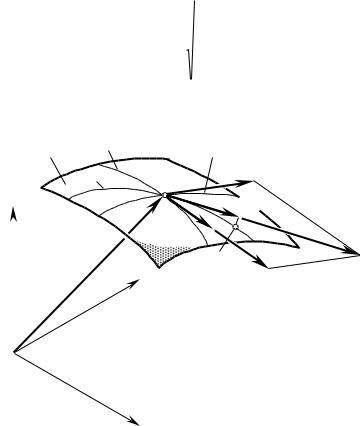
|
|
1.2. Задание рабочих поверхностей деталей и инструментов. |
39 |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
Расчет элементов их локальной геометрии |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
Y |
|
Z |
и |
|
2 |
|
Z |
и |
|
X |
и |
|
2 |
|
X |
и |
|
|
Y |
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|||||||||
Nи |
|
Nи |
|
|
|
Uи |
|
Uи |
|
|
|
Uи |
|
Uи |
|
|
|
Uи |
|
Uи |
|
. |
||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
Yи |
|
|
Zи |
|
|
|
|
|
Zи |
|
|
|
Xи |
|
|
|
|
Xи |
|
|
Yи |
|
|
|
|
||||
|
|
|
|
|
|
|
Vи |
|
Vи |
|
|
|
|
Vи |
|
|
Vи |
|
|
|
Vи |
|
|
Vи |
|
|
|
|||||||||
С учетом изложенного приходим к уравнению
|
Д И |
|
|
Vд u линия |
|
|
Uд u линия |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xиn XиM |
|
|
|
yиn YиM |
|
|
zиn ZиM |
|
. |
|||||||||||||||||||||||||||||||||
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d Uд и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
cos |
|
|
|
|
|
|
cos |
|||||||||||||||||
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Это уравнение задает прямую, |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
drд и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Zд u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
проходящую |
|
через |
точку M |
в |
нап- |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
d Vд и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
равлении нормали к исходной инстру- |
|
||||||||||||||||||||||||||||||||
|
|
|
rд u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ментальной |
|
поверхности. |
|
Здесь |
обо- |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
значено: x n , |
|
y n и |
z |
n |
|
– координаты |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d L д и |
|
|
|
|
|
|
|
и |
|
|
|
|
и |
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d Vд и |
|
|
|
|
|
|
текущей точки этой прямой. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
Yд u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Первая |
|
|
|
основная |
|
квадратичная |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
форма |
|
поверхности |
Д И . |
|
Задание |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
поверхности |
|
Д И |
уравнением |
в |
век- |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
торной форме позволяет наглядно ин- |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
терпретировать геометрический |
смысл |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ее |
первой |
|
|
основной |
|
квадратичной |
|
|||||||||||||||||||
|
|
|
|
|
|
|
Xд u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
формы. Для этого рассмотрим лежащую |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
на поверхности Д(И) линию l |
|
(рис. 1.8), |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
которую определим так |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Рис. 1.8. К определению первой основной квадратичной формы |
|
|
|
|
rд и Uд и t |
,Vд и t |
rд и t , |
|
(1.18) |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ф1.д u поверхности |
|
Д И . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
где t – параметр кривой l . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Если точка смещается вдоль линии l из положения |
|
M в положение |
M * , |
то вектор drд и определит |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
инфинитезимальное перемещение этой точки. Ограничиваясь рассмотрением только членов первого порядка |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
малости, получим |
|
|
|
rд и |
|
|
|
|
|
|
|
rд и |
|
|
|
|
|
|
|
|
rд и |
|
|
Uд и |
|
|
|
rд и |
|
|
Vд и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
dr |
д и |
|
dU |
д и |
|
|
|
dV |
|
|
|
|
|
|
dt |
|
|
dt. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
U |
д и |
|
|
|
V |
|
|
д и |
|
|
U |
д и |
|
|
t |
|
|
|
|
V |
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Здесь |
rд и |
|
d Uд и , |
|
rд и |
|
d Vд и , |
|
rд и |
|
Vд и |
|
d Vд и , |
|
rд и |
|
|
|
rд и |
|
Vд и |
|
d Lд и , |
|
|||||||||||||||||||||||||||||||||||||||
|
U |
д и |
|
V |
|
|
|
V |
|
U |
д и |
|
U |
д и |
V |
U |
д и |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
д и |
|
|
|
|
|
|
|
|
|
д и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
|
|
|
|
|
|
|
|
|
||||||||||||||||
а величины всех производных рассчитываются в точке M . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
Поскольку векторы d Uд и и |
d Vд и определяют касательную плоскость, |
то вектор |
drд и |
|
смещения |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
точки также лежит в этой плоскости. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
В предположении, что dUд и 0 , смещение drд и равно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
д и |
|
|
r |
д и |
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
dr |
д и |
|
|
|
|
|
|
|
|
|
|
д и |
dU |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.19) |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
V |
|
|
|
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
|
|
|
|
|
|
|
|
|
|
|
|
д и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
|
|
|
|
д и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
