Добавил:

Mehanik Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Технический Университет им. Р.Е. Алексеева

Предмет:

Технология машиностроения

Файл:

Radzevich, S.P. Monograph - 2001

.pdf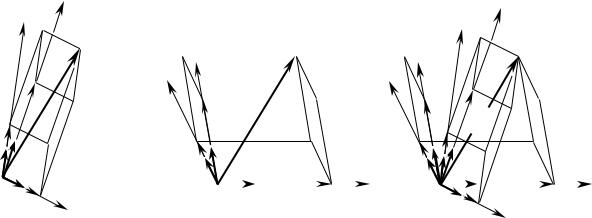

Скачиваний:

Добавлен:

23.02.2023

Размер:

24.47 Mб

Скачать

☆

<<< < Предыдущая 7 8 9 10 11 12 13 14 15 16 17 1819 / 6019 20 21 22 23 24 25 26 27 28 29 30 31 > Следующая >>>

180

3. Системы координат и линейные преобразования

M rx1 , r y1 , rz1

, r

M rx

,r y

,r z

, r

r y

О i1

Рис. 3.10. Базисы косоугольных систем координат.

	M		m11	m12	m13			t11	t21		t31		T T
(3.23)	M	1 2	m	m	m		t		t	22	t	32	T T	,
		1 2	21	22	23			12		22		32
			m	m	m			t	t	23	t	33
			31	32	33			13		23		33
будет матрицей перехода от первой системы координат								X1Y1Z1 ко второй системе координат							X2Y2 Z2 . Ее
i й столбец, совпадающий с		i й строкой матрицы				T , состоит из координат нового базиса									i 2 , j2 , k 2 ,

выраженных в исходном базисе i1 , j1 , k 1 .

Найдем зависимость новых координат вектора r от исходных его координат. Для этого представим

вектор r	через базисные векторы исходного X1Y1Z1 и нового					X2Y2 Z2 базисов:
(3.24)	r rx i1	ry	j1	rz	k 1 ;
	1	1		1
(3.25)	r rx i2	ry	j2	rz		k 2 .
	2	2		2

Воспользовавшись формулами (22), в разложении (25) новые базисные векторы выразим через исходные:

r rx2 t11i1 t12 j1 t13k 1 ry2 t21i1 t22 j1 t23k 1 rz2 t31i1 t32 j1 t33k 1 .

Приведя в этом соотношении подобные члены, получим

(3.26)	r t11rx	t21ry	t31rz	i1	t12rx	t22 ry	t32 rz	j1	t13rx	t23ry	t33rz	k 1 .
	2	2	2		2	2	2		2	2	2

Так как равенства (24) и (26) выражают один и тот же вектор в одном и том же базисе, то в силу единственности разложения вектора соответственные координаты в этих равенствах должны совпадать:

rx1 t11rx2 t21ry2 t31rz2 ; ry1 t12 rx2 t22ry2 t32rz2 ; rz1 t13rx2 t23ry2 t33rz2 ,

3.6. Косоугольные системы координат

181

откуда после замены tki на mik находим

rx	m11rx	m12ry	2		m13rz ;
1	2		2		2
ry	m21rx	m22ry		2	m23rz	;	(3.27)
1	2			2	2
rz	m31rx	m32ry	2		m33rz	.
1	2		2		2

В равенствах (27) исходные координаты вектора выражены через его новые координаты. Решая систему уравнений (27) относительно неизвестных rx2 , ry2 , rz2 , получаем

rx	s11rx	s12ry s13rz ;
2	1		1		1
ry	s21rx	s22 ry s23rz				;	(3.28)
2	1		1		1
rz	s31rx	s32 ry s33rz ,
2	1		1		1
где коэффициенты правых частей образуют матрицу
		s	s	s
	S	11	12	13		,
	S	s21 s22		s23		,
			s32
		s31	s32	s33

обратную матрице M1 2 :
S M1 2 1 .			(3.29)
В приведенных формулах использованы матрицы M1 2 ,	S и	T . Матрица	T – это таблица,

составленная из коэффициентов равенства (22), определяющих зависимость новых базисных векторов от исходных. Матрица S – это таблица из коэффициентов формул (28), характеризующих зависимость новых

координат вектора от исходных его координат. Матрица перехода M1 2 служит таблицей в формулах (27),

устанавливающих зависимость исходных координат от новых.

Матрицы M1 2 , S и T несобственные и тесно связаны одна с другой. Из определяющих матрицы

				1	T	T	1
M1 2 , S соотношений (23), (29) и правила транспонирования обратной матрицы				A		A	,

получим S M1 2 1 , T M1 2 T , S T T 1	и T S T 1.
Если матрицу A можно выразить через матрицу	B по формуле A	B T	1 , то справедливо также и

обратное равенство B A T 1 . Такие матрицы являются контрградиентными одна другой. Из изложенного следует:

Правило 3.1. Если зависимость новых базисных векторов от исходных определяется матрицей коэффициентов T , то зависимость новых координат вектора от исходных его координат определяется

матрицей S , контрградиентной матрице T .

Рассматривая вопрос преобразования косоугольных координат, Faux, I.D. и Pratt, M.J. (1987) отмечают, что применение косоугольных координат удобно в случаях, когда базисные векторы взаимно не ортогональны. На рис. 3.11 положение каждой точки плоскости, проходящей через точки A , B , O ,

определяется радиус-вектором r αa βb с началом в точке

, где

при условии, что

O A,

O B

182		3. Системы координат и линейные преобразования
a b 0 . Таким образом		точку O можно считать началом косоугольной системы осей с координатами
α,β . Длины отрезков
	O A и O B определяют масштабы вдоль этих осей.

Абсолютные

координаты

точки

P α, β определяются

соотношением r αa βb c , где

c OO .

Р ,

Если

A ,

B ,

лежат в одной

плоскости OXY, это

уравнение можно так представить в матричном виде:

b c

R Y

a2 b2

β .

Рис. 3.11. К преобразованию косоугольных

0 0 1

координат (Faux, I.D., and

где

0 T ,

1 –

декартовы

Pratt, M.J., 1987).

компоненты векторов a ,

b , c соответственно.

В трехмерном пространстве абсолютный радиус-вектор можно представить при помощи трех не

компланарных векторов a ,

b , c

и радиус-вектора ro , определяющего положение начала системы координат,

т.е.: r ro λa μb νc.

Это уравнение представимо в матричной форме

Детерминант этой матрицы задается величиной

a b c ;

он не равен нулю, т.к. a , b , c не

компланарны. Параметры λ , μ , ν являются косоугольными координатами по отношению к осям с началом в

ro и с направляющими векторами a , b , c соответственно.

3.6.2.Построение ортонорминованного базиса. По заданному произвольному базису i1 , j1 , k 1 можно (Клиот-Дашинский М.И., 1974) построить ортонормированный базис i N , j N , k N – базис, векторы которого

попарно ортогональны и имеют норму, равную единице (ортонормированному базису соответствует

прямоугольная декартова система координат). Найдем сначала вспомогательный базис i2 , j2 ,

k 2 , векторы

которого попарно ортогональны, но могут иметь норму, не равную единице.

Первый базисный вектор определим как

i2 i1 . Ясно, что

i2 0 , т.к.

вектор i1 ненулевой, ибо он

входит

в линейно

независимую систему i1 ,

j1 , k 1 .

Второй

базисный

вектор определим формулой

j2 j1

ν1i2 , где скаляр ν1 подобран так, чтобы вектор j2

был ортогонален вектору i2 (рис. 3.12):

j2 i 2 j1 ν1i2 i2 j1 i 2 ν1i 2i2 0.

Следовательно,

. Знаменатель этой дроби

i2 i2

не равен нулю,

т.к.

i2 0 . Поэтому и j2

– ненулевой

i1 i

вектор, ибо векторы i1 и j1

линейно независимы.

Допустим, что попарно ортогональные ненулевые

векторы

и j2 уже определены. Построим вектор k 2 .

Рис. 3.12. К построению ортонормированного

Для этого

положим

k 2 k 1 2i1 3 j2

и определим

числа ν2 и

ν3

из условия ортогональности вектора k 2

базиса.

3.6. Косоугольные системы координат								183
векторам k 2 и j2 : k 2 i2 k 1 i 2 2i2 i2 и k 2	j2 k 1	j2	3 j2 j2 . Откуда 2			k 1	i2	и 3	k 1 j2	.
						i 2 i2
									j2 j2
Знаменатели этих дробей не равны нулю, т.к.	i2 0 ,	j2	0 . Поэтому и k 2	–	ненулевой вектор, т.к. он
выражается в виде линейной комбинации линейно независимых векторов				i1 ,	j1 ,		k 1	с ненулевыми
коэффициентами.

Построенные ненулевые векторы i2 , j2 , k 2 попарно ортогональны и линейно независимы.

Так как векторы i2 , j2 , k 2 линейно независимы, то они образуют базис в трехмерном пространстве.

Если каждый из векторов разделить на его норму, получим векторы i N	i2	;	j N	j2	;	k N	k 2	,
	i2			j2			k 2

образующие ортонормированный базис.

Рассмотренный способ построения ортонормированного базиса по заданной линейно независимой системе называют процессом ортогонализации системы векторов.

Пример 3.7. Построим ортонормированную систему векторов по линейно независимой системе i1 1, 1, 0 , j1 1, 1, 1 ,

k1 1, 3, 3 . Координаты векторов заданы в естественном базисе.

1.Построим вспомогательную систему i 2 , j2 , k 2 , векторы которой попарно ортогональны:

а). i2 i1 1, 1, 0 ;

б). j2 j1 1i2 , 1			j1 i 2					2	1 ,		j2 1, 1, 1 1, 1, 0 0, 0, 1 ;
б). j2 j1 1i2 , 1								2	1 ,		j2 1, 1, 1 1, 1, 0 0, 0, 1 ;
			i2 i2					2
в). k 2 k 1 ν2i2 ν3 j2 ,					ν2		k 1 i 2					4	2 ,	ν3	k 1 j2			3		3 ,	k 2 1, 3, 3 2 1,1, 0 3 0, 0,1 1,1, 0 .
в). k 2 k 1 ν2i2 ν3 j2 ,					ν2								2 ,	ν3						3 ,	k 2 1, 3, 3 2 1,1, 0 3 0, 0,1 1,1, 0 .
								i 2 i 2			2				j2 j2		1
2. Построим ортонормированную систему:
	i	2			1			1								j	2		0, 0, 1 ;				k		1		1
i N		2				,				, 0	;				j N		2					k N		2		,		, 0	.
i N						,				, 0	;				j N							k N				,		, 0	.
	i	2						2								j	2						k 2		2		2
	i	2		2				2								j	2						k 2		2		2

Для локального репера с началом на поверхности Д И

направления касательных

rд и

Uд и

Vд и

могут быть взаимно перпендикулярными (в этом случае

rд и

0 ), тогда векторы

rд и

U д и

Vд и

Uд и

Nд и (здесь Nд и

rд и

) образуют локальный ортогональный базис в точке. Если направления

д и

касательных взаимно не перпендикулярны, такой базис можно построить несколькими путями. Например,

rд и	,	m	и Nд и формируют такой базис, если мы определим	m Nд и	rд и	. Далее переход к
Uд и					U д и

ортонормированному базису очевиден.

3.6.3. Преобразования косоугольных координат. Преобразования косоугольных координат удобно рассмотреть в такой последовательности: сначала рассмотрим параллельный перенос систем координат в пространстве, а затем поворот систем координат.

3.6.3.1 Параллельный перенос систем координат. Исходная система координат X1Y1Z1 с началом координат в точке O1 (рис. 3.13.1) переносом на вектор d1 2 преобразуется в систему координат X2Y2 Z2 с началом координат в точке O2 . Оси X2 , Y2 , Z2 параллельны соответствующим осям X1 , Y1 , Z1 исходной системы координат. Параллельный перенос описывается следующими формулами:

X2 X1 d x ;

Y2 Y1 d y ;

Z2 Z1 d z .

184

3. Системы координат и линейные преобразования

Y M

d1 2

Y M

1 2

d y

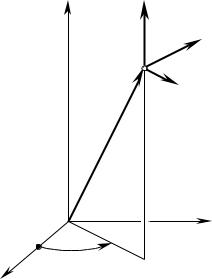
Рис. 3.13. Преобразования косоугольных координат: параллельный перенос начала координат.

Аналогичное имеет место при параллельном переносе косоугольных систем координат на плоскости (рис.3.13.2). Поэтому приведенные формулы справедливы и для вырожденного случая преобразованя координат на плоскости.

3.6.3.2. Поворот систем коор-

динат. Поворот декартовой системы координат X1Y1Z1 вокруг

проходящей через начало коорди-

нат оси	g	(рис. 3.14.1)		с
направляющими			косинусами
cos X1, g ,		cos Y1, g ,
cos Z1, g		на	угол

переводит ее в систему коориднат X2Y2 Z2 . Такое преобразование

координат описывается формулами:

X2 X1 cos 2 1 cos Y1 sin 1 cos Z1 sin 1 cos ;

Y2 X1 sin 1 cos Y1 cos 2 1 cos Z1 sin 1 cos ;

Z2 X1 sin 1 cos Y1 sin 1 cos Z1 cos 2 1 cos .

Если известны направляющие косинусы углов между осями декартовой системы координат систем координат X1Y1Z1 и X2Y2 Z2 с общим началом, то справедливы следующие формулы:

X2 l1 X1 m1Y1 n1Z1 ;

Y2 l2 X1 m2Y1 n2 Z1 ;

X3 l3 X1 m3Y1 n3 Z1 ,

Y M

X2 где li ,

mi , ni – направляющие

косинусы (i 1, 2, 3 ).

В векторной форме:

X2 Rs 1 2 X1 ,

X1 X1 X1 , Y1, Z1 и

где

Рис. 3.14. Преобразование косоугольных координат: поворот

системы координат.

X2 X2 X2 , Y2 , Z2 . Оператор результирующего преобразования координат может быть представлен в матричной форме:

3.6. Косоугольные системы координат							185
	l1	l2		l3		0
Rs	m	m		m		0
Rs	1 2 1	n	2	n	3	.
	n	n		n		0
	1		2		3
	0	0		0		1

где матрица в правой части является ортогональной.

Если заданы две системы координат X1Y1Z1 и X2Y2 Z2 с общим началом координат и известны косинусы углов между положительными направлениями осей X1 , Y1 , Z1 системы X1Y1Z1 и осей X2 , Y2 , Z2 системы X2Y2 Z2 , а также косинусы xy , yz , xz координатных углов системы координат X1Y1Z1 , то, зная положение точки M в системе координат X2Y2 Z2 , можно вычислить положение той же точки в системе координат X1Y1Z1 . В этом случае следует воспользоваться такими формулами:

1 2

xy yz

;

1 2

;

1 2

где:

X X2 cos X2 , X1 Y2 cos Y2 , X1 Z2 cos Z2 , X1 ;

Y X2 cos X2 , Y1 Y2 cos Y2 , Y1 Z2 cos Z2 , Y1 ;

Z X2 cos X2 , Z1 Y2 cos Y2 , Z1 Z2 cos Z2 , Z1 .

Поворот косоугольных

координат на

плоскости производится так.

Система координат

X1Y1Z1 с

координатным углом xy при повороте на

угол

переходит в систему координат X2Y2 Z2 .

При этом

формулы преобразования координат имеют вид:

sin xy

sin

;

sin

sin xy

Y .

sin xy

Очевидно, что приведенные формулы являются частным (вырожденным) случаем соответствующих формул преобразования косоугольных координат в пространстве.

Если xy 90 , получим: X2 X1 cos Y1 sin и Y2 X1 sin Y1 cos .

186	3. Системы координат и линейные преобразования

3.7. Криволинейные системы координат

Для упрощения преобразований на некоторых этапах решения задач формообразования поверхностей деталей и профилирования режущего инструмента удобно от ортогональной системы декартовых координат перейти к криволинейным координатам в пространстве, а после решения задачи в криволинейных координатах совершить обратный переход к прямоугольным декартовым координатам. Возможность упрощения при этом формы записи уравнений очевидна из следующего простого примера. Если в декартовой

системе координат уравнение сферы радиуса R с центром в

Z		ez
		e
		e
		z
	r	Y
X
Рис. 3.15. К образованию оператора
перехода Cl z, , .

начале координат имеет вид X 2 Y2 Z 2 R2 , то та же сфера в сферических координатах будет описана уравнением R Сonst , что существенно проще.

Преобразования криволинейных координат рассмотрим на примере цилиндрических и сферических систем координат.

3.7.1.Взаимосвязь между ортогональными декартовыми

ицилиндрическими координатами. Геометрическая информа-

ция о поверхностях детали и инструмента может быть представлена в цилиндрических коодинатах. Переход от ортогональной декартовой системы координат к системе цилиндрических координат производится путем переноса на r вдоль оси X , после которого следует поворот на угол вокруг оси Z и далее следу-

ющий перенос на z вдоль оси Z (рис. 3.15). Следовательно:

Cl z, , Tr z, Z Rt , Z Tr r, X

cos		sin	0	r cos

sin		cos	0	r sin .
	0	0	1	z
	0	0	0	1
	0	0	0	1

В цилиндрических координатах положение текущей точки M на поверхности Д И определяется полярными координатами M и ρ M ее проекции на плоскость XY и аппликатой Z M (рис. 3.16.1). Через эти координаты радиус-вектор r M текущей точки M на поверхности Д И выражается так

				r M M e Z M k ,
где e – орт радиус-вектора ρ M проекции точки M на координатную плоскость XY .
Координатные поверхности представляют собой:
-	ρ Const – круговые цилиндры с осью OZ ;
-	Сonst	– плоскости, проходящие через ось Z ;
-	Z Const – плоскости, параллельные плоскости координат XY ,
а координатные линии:				(окружности с центром на оси	Z , расположенной в плоскости,
-	Var ,	ρ Cosnt ,	Z Const	(окружности с центром на оси	Z , расположенной в плоскости,
	параллельной плоскости координат XY );
-	Const ,	ρ Var ,	Z Сonst	(прямые, проходящие через ось Z	параллельно плоскости координат
	XY );		Z Сonst (прямые, параллельные оси Z ).
-	Const , ρ Var ,		Z Сonst (прямые, параллельные оси Z ).

Каждой точке M ставится в соответствие три единичных вектора e , e ρ , e z k , которые касательны к координатным линиям и указывают направление возрастания соответствующей координаты как параметра.

где V M , VρM , VzM

3.7. Криволинейные системы координат

187

eZ k

M M , M , Z

Z M

r M

X M

Z M

Y M

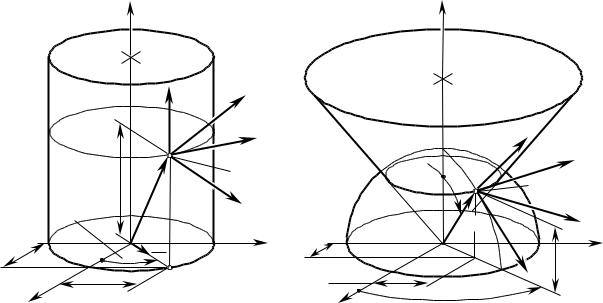
Рис. 3.16. Цилиндрические и сферические системы координат.

В противоположность базисным векторам i , j , k прямоугольной декартовой системы координат, единичные векторы e , e , e z изменяются при переходе от одной точки поверхности Д И к другой ее точке. Но в любой точке M они всегда взаимно перпендикулярны и образуют правую систему координат.

Если некоторый вектор V M разложить по направлениям единичных векторов e , e , e z , получим

V M V M e VρM e ρ VzM e z ,

– цилиндрические координаты некоторой точки M на поверхности Д И – в противоположность декартовым координатам VxM , VyM , VzM , которые используются в

разложении V M VxM i VyM j VzM k .

Декартовы координаты текущей точки M на поверхности Д И выражаются через ее цилиндрические координаты по формулам

Vx V sin Vρ cos ;

Vy V cos Vρ sin ;

Vz VZ .

Цилиндрические координаты точки M выражаются через ее декартовы координаты по формулам

V Vx sin Vy cos ;

Vρ Vx cos Vy sin ;

Vz Vz.

188

3. Системы координат и линейные преобразования

Линейный элемент поверхности Д И в цилиндрической системе координат равен

1.д и

д и

2 dρ2

dZ 2

д и

Декартовы и цилиндрические координаты текущей точки M на поверхности

Д И

связаны между

собой соотношениями (см. рис. 3.16.1):

Y M

tan

ρ M

M 2

;

X M

ρ M cos M ;

Y M ρ M sin M ;

Z M

Z M ,

где X M , Y M , Z M – декартовы координаты текущей точки M на поверхности

Д И ;

ρM – радиус цилиндра, проходящего через точку M ;

M – полярный угол точки M .

При решении задач на плоскости Z M 0 . В этом случае цилиндрические координаты вырождаются в полярные, которые с декартовыми координатами на плоскости связаны соотношениями:

M arctan

X M

ρ M cos M ;

;

(3.30)

sin

ρ M

X M

Y M

3.7.2. Взаимосвязь между ортогональными декартовыми и сферическими координатами.

Рассмотрим определение положения вектора при помощи сферических координат. Переход от ортогональной декартовой системы координат к системе сферических координат производится путем переноса на r вдоль оси Z , за которым следует поворот на угол вокруг оси Y и

затем поворот на угол вокруг оси Z (рис. 3.17):							Z	er
								er
Sph , , r Rt , Z Rt , Y Tr r, Z								e
cos cos			sin	cos sin	r cos sin
cos cos			sin	cos sin	r cos sin			e
			cos	sin sin	r sin sin			e
sin cos			cos	sin sin	r sin sin	.
	sin		0	cos	r cos
	0		0	0	1
	0		0	0	1
В сферических координатах положение текущей точки M на								r
В сферических координатах положение текущей точки M на
поверхности	Д И	определяется ее географическими координа-
тами M и ψ M		на сфере текущего радиуса r M с центром в						Y
начале координат и проходящей через эту точку (рис. 3.16.2).								Y

Радиус-вектор точки M выражается через эти координаты так:							X
			r e cosψ k sin ψ .				Рис. 3.17. К образованию оператора
							Рис. 3.17. К образованию оператора
Координатные поверхности представляют собой:							перехода Sph , , r .

				3.7. Криволинейные системы координат	189
- r Const		– сферы;
-	Const	– плоскости, проходящие через ось Z ;
-	ψ Const	– конусы вращения с осью, совпадающей с осью Z и вершиной, расположенной в начале
		координат,
а координатные линии:				– параллели (широты);
-	Var ,	ψ Const ,	r Const	– параллели (широты);
-	Const , ψ Var ,		r Const	– меридианы (долготы);
-	Const , ψ Const , r Var			– прямые, проходящие через начало координат.	Д И ставятся
Как и в случае применения цилиндрических координат, каждой точке M на поверхности					Д И ставятся

в соответствие единичные векторы e , e , er , которые касательны к соответствующим координатным линиям, идущим в направлении возрастания значений соответствующего параметра.

Если некоторый вектор V M разложить по единичным векторам e , e , er , получим

V M V M e VψM eψ Vr M er ,

где V , Vψ , Vr – сферические координаты текущей точки M на поверхности Д И . Декартовы координаты выражаются через сферические координаты по формулам:

Vx V sin Vψ cos cosψ Vr cos sin ψ;

Vy V cos Vψ sin cosψ Vr sin sin ψ;

Vz Vψ sin ψ Vr cos ψ.

Сферические координаты выражаются через декартовы координаты по формулам:

V Vx sin Vy cos ;

Vψ Vx cos cosψ Vy sin cosψ Vz sin ψ;

Vr Vx cos sin ψ Vy sin sin ψ Vz cos ψ.

Единичные векторы e , eψ , er взаимно перпендикулярны и образуют правую систему координат. Линейный элемент поверхности Д И в сферической системе координат можно рассчитать по формуле:

1.д и

dr 2

dψ

cos ψ

dψ2

д и

Декартовы и сферические координаты текущей точки

M на поверхности

Д И

связаны между собой

зависимостями (см. рис. 3.16.2):

Y M

Z M

M 2

;

tan

cos ψ

X M

Y M

Z M

X M r M cos M sin ψ M ;

Y M r M sin M sin ψ M ;

Z M r M cos ψ M .

Здесь X M , Y M , Z M – декартовы координаты текущей точки M на поверхности Д И ;

<<< < Предыдущая 7 8 9 10 11 12 13 14 15 16 17 1819 / 6019 20 21 22 23 24 25 26 27 28 29 30 31 > Следующая >>>

Соседние файлы в предмете Технология машиностроения

#
23.02.202324.47 Mб11Radzevich, S.P. Monograph - 2001.pdf
#
23.02.20237.23 Mб4Горбацевич - Курсовое проектирование по ТМ.doc
#
23.02.2023949.47 Кб3Мешкова - Организация Технологии Отрасли.pdf
#
23.02.20234.4 Mб1Оптимизация Технологических Систем (укр).pdf
#
23.02.2023882.47 Кб3Основные Положения Теории Базирования (Лекции).pdf
#
23.02.20231.01 Mб6Основы Проектирования ТП.pdf