
Radzevich, S.P. Monograph - 2001
.pdf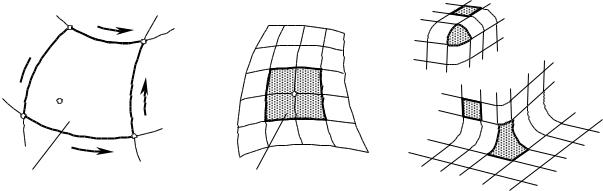
70
Uд 0
Vд 1
rд(0,Vд) 
Uд 0
Vд 0
Дi
1. Рабочие поверхности деталей и инструментов
 rд(U д,1)
rд(U д,1)
|
Uд 1 |
|
|
rд(Uд,Vд) |
Vд 1 |
|
|
rд(1,Vд) |
|
|
|
|
|
|
|
rд(U д,0) |
Uд 1 |
|
|
V 0 |
|
|
|
|
д |
Дi |
|
|
|
|
|
1. |
|
2. |
3. |
Рис. 1.14. Примеры отсеков обрабатываемой поверхности детали: выделенный отсек параметрически
заданной поверхности Д (1); сопряженные отсеки поверхности Д (2); 3-х, 4-х и 5-и угольные отсеки поверхности Д (3).
метрии находятся как для поверхностей, заданных аналитически. Решение задачи синтеза наивыгоднейшего формообразования дискретно заданных сложных поверхностей деталей на многокоординатных станках с ЧПУ в этом случае связано с решением дополнительной задачи аппроксимации формообразуемой поверхности Д , например, полиномиальными сплайнами, с широким использованием для этого методов вычисли-
тельной геометрии.
Уравнение поверхности Д(И) деталей и инструментов. Алгебраическая форма отсека поверхности Д ,
описанного бикубическим сплайном, имеет вид:
|
3 |
3 |
(1.62) |
rд Uд, Vд ai jUдiVдj , |
|
|
i 0 j 0 |
|
где a i j – векторные коэффициенты.
Выпишем уравнение (62) в развернутом виде и расположим его члены в таком порядке:
r |
д |
U |
д |
,V |
a U |
3V |
3 |
a U |
3V |
2 |
a U |
3V a |
U |
3 |
|
|||
|
|
д |
33 |
д д |
32 |
д д |
31 |
д д |
30 |
|
д |
|
||||||
|
|
|
|
|
a U |
2V3 |
a U |
2V 2 |
a U |
2V a |
|
U |
2 |
|
||||
(1.63) |
|
|
|
|
23 |
д |
д |
22 |
д |
д |
21 |
д д |
20 |
д |
|
|||
|
|
|
|
a U V |
3 |
a U V |
2 |
a |
U V aa U |
|
|
|||||||
|
|
|
|
|
д |
|||||||||||||
|
|
|
|
|
13 |
д д |
12 |
д д |
11 |
д д |
10 |
|
|
|||||
|
|
|
|
|
a V |
3 |
a V2 |
|
a |
|
V a |
00 |
. |
|
||||
|
|
|
|
|
03 д |
|
02 д |
|
|
01 д |
|
|
|
|||||
Этот 16-членный полином – вектор-функция скаляров |
Uд |
и |
Vд , определяет все точки, лежащие на |
|||||||||||||||
отсеке поверхности детали.
Алгебраической форме (63) бикубического отсека поверхности детали соответствует матричная форма
записи его уравнения: |
|
|
|
|
(1.64) |
rд |
~ |
~ |
T |
Uд |
A Vд |
, |
||
где обозначено: |
|
|
|
|
1.2. Задание рабочих поверхностей деталей и инструментов. |
|
Расчет элементов их локальной геометрии |
71 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a33 |
a32 |
a31 |
||
~ |
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
a |
|
a |
|
|
U |
3 |
U |
2 |
U |
|
1 T |
; |
V3 |
V 2 |
V 1 T |
a |
22 |
21 |
||||
U |
д |
д |
V |
; A 23 |
|
|
||||||||||||
|
|
д |
|
д |
|
|
|
д |
д |
д |
д |
a13 |
a12 |
a11 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a 02 |
a 01 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a 03 |
||||
a30
a 20 . a10
a 00
Обратим внимание на то, что индексы векторных элементов матрицы A соответствуют индексам в
развернутом уравнении (63).
Рассмотрим случай, когда произвольный отсек сложной поверхности детали ограничен двумя парами кривых – граничными кривыми, и дискретно задан так: известны координаты rдi четырех его вершин
i 1, 2, 3, 4 , в каждой вершине определены |
направления касательных |
rд |
|
|
|
и |
rд |
|
|
к каждой из |
||||||||||
Uд |
Vд |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
i |
|
i |
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
граничных кривых и, кроме того, в каждой вершине известен вектор кручения |
|
|
|
2rд |
|
|
|
. Исходя из этих |
||||||||||||
Uд Vд |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
i |
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
данных геометрическая форма бикубического отсека поверхности |
Д приводится к виду: |
|
|
|
|
|
|
|
||||||||||||
r |
|
|
~ |
|
|
~ |
Т. |
|
|
|
|
|
(1.65) |
|||||||
д |
U |
д |
М B М 1 V |
|
|
|
|
|
||||||||||||
|
|
|
|
д |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где матрица коэффициентов равна:
|
(1) |
|
|
|
|
||
|
r |
|
|
|
|
|
|
|
д |
|
|
|
|
|
|
|
r (4) |
|
|
|
|
||
|
|
|
|
|
|||
|
д |
|
|
|
|
|
|
e |
rд |
|
|
|
|
||
|
|
|
|
||||
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
U |
д |
|
|
||||
|
|
|
|
1 |
|||
|
|
|
|||||
|
r |
д |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
||
|
U д |
|
|
|
|
||
|
|
|
|
|
4 |
||
|
|
|
|
||||
(2) |
|
|
|
|
|
rд |
|
|
|
|
|
|
||
rд |
|
|
|
|
|
|
|
|
|
|
||||
|
Vд |
|
1 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||
(3) |
|
|
|
|
|
rд |
|
|
|
|
|
|
||
rд |
|
|
|
|
|
|
|
|
|
|
||||
|
Vд |
|
4 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||
rд |
|
|
|
|
2rд |
|
|
|
||||||
|
|
|||||||||||||
U д |
|
|
2 |
U д Vд |
|
1 |
||||||||
|
|
|||||||||||||
|
|
|
|
|||||||||||
rд |
|
|
|
|
2rд |
|
|
|||||||
|
||||||||||||||
U д |
|
3 |
U д Vд |
|
4 |
|||||||||
|
||||||||||||||
|
|
|
|
|
||||||||||
|
rд |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vд |
|
|
|
|
|
|
|
|
|
||||
|
|
|
2 |
|
|
|
|
|
r (i) |
|||||
|
|
|
|
|
|
|||||||||
|
r |
д |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Vд |
|
|
3 |
|
|
|
|
|
д |
||||
|
|
|
|
|
|
|
||||||||
|
2 |
rд |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||
U |
|
V |
|
|
|
|
rд |
|||||||
|
|
д |
|
|
|
|
|
д |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
V |
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
rд |
|
|
|
|
|
|
|
|
|
д |
||
|
|
|
|
|
|
|
|
|
|
|
||||
U |
д |
V |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
д |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
r |
д |
|
|
|
|
|
||
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||
U д |
|
|
|||||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
i |
|
|
(1.66) |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
2 |
rд |
|
|
|
|
|
||
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||
|
U |
д |
V |
|
|
|
|||||
i |
|
|
|
|
|
д |
i |
|
|
||
|
|
|
|
|
|
|
|
|
|
||
Сопоставляя (65) и (64) видим, что
B M 1 A M T 1.
Для рассматриваемого случая дискретного задания поверхности Д матрица M 1 равна
|
0 |
0 |
0 |
1 |
|
M |
|
|
|
|
|
1 1 |
1 |
1 |
1 . |
(1.67) |
|
|
0 |
0 |
1 |
0 |
|
|
|
2 |
1 |
|
|
|
3 |
0 |
|
||
Например (Dinauer, W.R., Daffie, N.A., |
Philpott, M.L., |
1994), если отсек поверхности Д |
представлен |
||
вектором

72 |
|
|
|
1. Рабочие поверхности деталей и инструментов |
|
|
||||||||||||||||
r |
д |
U |
д |
,V |
X |
д |
U |
д |
,V |
|
Y |
U |
д |
,V |
|
Z |
д |
U |
д |
,V |
|
1 Т, |
|
|
д |
|
|
д |
|
д |
|
д |
|
|
|
д |
|
|
|||||||
где параметры Uд и Vд пронормированы, т.е. изменяются от 0 до 1, то он может быть переписан в Эрмитовой форме (Mortenson, M., 1985)
|
|
|
|
|
|
|
|
|
|
|
U |
д |
M |
h.д |
Q |
x.д |
MT |
|
VT |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h.д д |
|
|
|
|
|
|
|
|||||||||
|
|
|
r |
|
|
U |
|
|
,V |
UдM h.дQ y.дMTh.дVдT |
, |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
д |
|
|
д |
д |
U |
д |
M |
h.д |
Q |
z.д |
MT |
|
VT |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h.д д |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где векторы Uд и Vд равны |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
д |
U 3 |
|
|
U |
2 |
U 1 ; |
|
|
V V3 |
|
|
V |
2 V 1 . |
|
|||||||||||||||||||
|
|
д |
|
|
|
|
|
д |
|
|
|
|
|
|
|
|
д |
|
|
|
|
д |
|
|
д |
|
|
д |
|
|
||||
Матрица Эрмита1 M h.д имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
M |
|
3 |
|
|
3 |
|
2 |
|
1 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
h.д |
|
0 |
|
|
0 |
|
|
1 |
|
|
|
0 |
|
. |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||||||||
Здесь Q x.д есть матрица, определяющая |
rд |
|
– компоненты вектора положения, касательные к Uд |
и |
||||||||||||||||||||||||||||||
Vд линиям, а также векторы кручения в четырех углах отсека: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
rд 0,0 |
rд 0,1 |
|
|
rд 0,0 |
|
rд 0,1 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
V |
|
|
|
|
V |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д |
|
|
|
|
|
|
д |
|
|
||
|
|
|
r |
д |
1,0 |
r |
д |
1,1 |
|
|
rд 1,0 |
|
r rд 1,1 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
V |
|
|
||||||||||
|
|
|
rд 0,0 |
rд 0,1 |
|
|
|
|
|
д |
|
|
|
|
д |
|
|
|||||||||||||||||
Q x.д |
2rд 0,0 |
2rд 0,1 . |
|
|||||||||||||||||||||||||||||||
|
|
|
|
U |
д |
U |
д |
|
|
|
U |
д |
|
|
|
U |
д |
V |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д |
|
|
|||||||
|
|
|
rд 1,0 |
rд 1,1 |
2rд 1,0 |
|
2rд 1,1 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
U |
д |
U |
д |
|
U |
д |
V |
|
|
|
U |
д |
V |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
д |
|
|
д |
|
|
|||||||||||
По форме матрицы Q y.д и Q z.д |
подобны матрице Q x.д . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
В алгебраической форме (64) аналитического описания бикубического отсека сложной поверхности |
Д |
|||||||||||||||||||||||||||||||||
переменными являются матрицы |
~ |
|
|
|
|
|
|
|
~ |
– соответственно первый и последний сомножитель. Матрица |
||||||||||||||||||||||||
Uд |
|
|
и Vд |
|||||||||||||||||||||||||||||||
A в качестве своих элементов содержит векторы a i |
j , каждый из которых является величиной постоянной – |
|||||||||||||||||||||||||||||||||
следовательно, матрицу A следует рассматривать как постоянную. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
Геометрическая форма (65) бикубического отсека сложной поверхности детали содержит переменные
матрицы |
~ |
и |
~ |
, также являющиеся первым и последним сомножителем соответственно. Произведение |
Uд |
Vд |
1Эрмит, Шарль (Hermite, Charles) (24.12.1822, Дьёз, – 14.1.1901, Париж), французский математик, член Парижской АН (1856). С 1848 работал в Политехнической школе, с 1869 – профессор Парижского университета. Эрмиту принадлежат исследования по различным вопросам классического анализа, алгебры и теории чисел. Основные работы связаны с теорией эллиптических функций и ее приложениями. Эрмит изучил класс ортогональных многочленов – многочлены Эрмита. Ряд работ Эрмита посвящены теории алгебраических форм и их инвариантов. Доказал (1873) трансцендентность числа e.
1.2. Задание рабочих поверхностей деталей и инструментов.
Расчет элементов их локальной геометрии |
|
73 |
|
|
|
матриц M B M T в (65) – величина постоянная. Это очевидно, во-первых, потому, что элементы матрицы |
||
B в (66) – величины постоянные и матрица (67) состоит из констант. Во-вторых, |
произведение |
|
M B M T A , где A , как было отмечено, является постоянной матрицей. |
|
|
Для различных способов задания бикубического отсека поверхности Д всегда имеем |
произведение |
|
нечетного количества матриц-констант, умноженного с обеих сторон на переменные матрицы |
~ |
~ |
Uд |
и Vд . |
|
Поэтому для расчета элементов локальной геометрии поверхности детали в виде отсека поверхности, описанного бикубическим сплайном, достаточно задать уравнение вида (64), с той лишь разницей, что
матрицу A будем рассматривать как произведение нечетного количества постоянных по величине матриц
Aд :
~ |
n |
|
~ Т |
|
|
rд Uд |
|
|
|
Vд , |
(1.68) |
|
Aq |
||||
|
|
|
|
|
|
|
q 1 |
|
|
|
|
где q – порядковый номер матрицы в произведении;
n – количество перемножаемых матриц.
Получение аппроксимационной формулы дает возможность перейти от дискретного задания к непрерывному аналитическому описанию поверхности детали уравнением, являющимся ее математической моделью.
Первые производные уравнения поверхности детали. Если дискретно заданная поверхность Д аналити-
чески описана бикубическим уравнением вида (68), то для нахождения необходимых производных уравнение
отсека этой поверхности удобно переписать в форме: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
3 3 |
|
|
n |
|
|
|
i |
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
rд Uд,Vд |
|
|
|
q |
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
ai j U |
дVд |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 0 j 0 q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
n |
q |
|
|
3 |
|
n |
|
q |
|
|
|
2 |
n |
|
q |
|
|
n |
|
q |
|
|
3 |
|
||
|
|
a |
V |
|
a |
|
V |
a |
V |
a |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
U |
д |
||||||||||||||||||
|
|
33 д |
|
|
|
32 |
|
д |
|
|
31 |
д |
|
|
30 |
|
|
|||||||||||
|
q 1 |
|
|
|
|
|
q 1 |
|
|
|
|
|
|
q 1 |
|
|
|
|
|
q 1 |
|
|
|
|
|
|
|
|
|
|
n |
q |
|
|
3 |
|
n |
|
q |
|
|
|
2 |
n |
|
q |
|
|
n |
|
|
|
|
|
2 |
|
|
|
|
a |
V |
|
a |
V |
a |
V |
a |
q |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
U |
|
д |
||||||||||||||||||
|
|
23 |
д |
|
q 1 |
|
22 |
|
д |
q 1 |
|
21 |
д |
q 1 |
|
20 |
|
|
|
|||||||||
|
q 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.69) |
||||
|
|
n |
|
|
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
q |
|
3 |
|
|
q |
|
|
2 |
q |
|
|
|
q |
|
|
|
|
||||||||||
|
|
a |
V |
|
a |
|
V |
a |
V |
a |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
10 |
U |
д |
|||||||||||||||||
|
13 д |
|
12 |
|
д |
|
11 |
|
д |
|
|
|
|
|||||||||||||||
|
q 1 |
|
|
|
|
|
q 1 |
|
|
|
|
|
|
q 1 |
|
|
|
|
|
q 1 |
|
|
|
|
|
|
|
|
|
|
n |
q |
|
|
3 |
|
n |
|
q |
|
|
|
2 |
n |
|
q |
|
|
|
n |
|
q |
|
|
|
|
|
|
|
a |
V |
|
a |
|
V |
a |
|
V |
a |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
; |
|
|
|
|
||||||||||||||||
|
|
03 д |
|
|
|
02 |
|
д |
|
|
01 |
д |
|
|
00 |
|
|
|
|
|||||||||
|
q 1 |
|
|
|
|
|
q 1 |
|
|
|
|
|
|
q 1 |
|
|
|
|
|
q 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
n |
|
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a33q |
a32q |
a31q |
a30q |
|
|
3 |
|
|
||||||||||
|
|
|
|
q 1 |
|
q 1 |
|
q 1 |
|
q 1 |
|
|
|
V |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
д |
|
||||||||||||
|
|
|
|
|
n |
|
|
n |
|
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
a q |
a q |
a q |
a q |
|
|
|
|
2 |
|
|
||||||||
3 |
2 |
U д |
q 1 |
|
23 |
q 1 |
|
22 |
q 1 |
21 |
q 1 |
|
20 |
|
|
Vд |
|
|
|||||
U д |
U д |
|
n |
|
|
n |
|
|
n |
|
|
n |
|
|
|
|
|
|
|
; |
|||
|
|
|
|
|
a13q |
a12q |
a11q |
a10q |
|
|
V |
|
|
|
|||||||||
|
|
|
|
q 1 |
|
q 1 |
|
q 1 |
|
q 1 |
|
|
|
|
д |
|
|
||||||
|
|
|
|
|
n |
a q |
n |
a q |
n |
a q |
n |
a q |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||||||||
|
|
|
|
|
|
03 |
|
02 |
|
01 |
|
00 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
q 1 |
|
q 1 |
|
q 1 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
q 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
74 |
|
|
|
|
1. Рабочие поверхности деталей и инструментов |
|
|
|
|
||||||||||||||||
|
|
|
U д3 |
|
|
Uд2 U д |
|
|
n |
|
|
|
Vд3 |
|
Vд2 |
|
|
|
|
|
|
||||
(1.70) |
|
|
|
1 |
|
aijq |
|
|
|
Vд |
1 T. |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
q 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из (70) находим, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
д |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
(1.71) |
|
|
|
|
|
|
3U д2 |
|
2Uд |
|
1 |
0 |
|
aijq |
|
Vд2 |
Vд |
Vд |
1 T ; |
||||||
|
|
|
|
|
|
||||||||||||||||||||
|
U д |
|
|
|
|
|
|
|
|
q 1 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.72) |
|
rд |
|
|
2 |
U д Uд |
1 |
|
|
n |
q |
|
|
2 |
2Vд |
1 |
0 |
T |
. |
||||||
|
V |
|
Uд |
aij |
|
3Vд |
|
||||||||||||||||||
|
|
|
д |
|
|
|
|
|
|
|
|
|
q 1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если матричную форму записи уравнений (71) и (72) производных развернуть и полученный результат сопоставить с уравнениями соответствующих производных, полученных путем дифференцирования уравнения (69), то будем видеть, что получен один и тот же результат.
Касательные к координатным линиям. Уравнения (71) и (72) первых производных уравнения (70)
поверхности Д И по U |
, V |
параметрам определяют векторы |
rд и |
и |
rд и |
, касательные к |
|
|
|
||||||
|
д и |
д и |
|
Uд и |
|
Vд и |
|
|
|
|
|
|
|||
координатным линиям для отсека поверхности, описанного бикубическим уравнением. По аналогии с рассмотренным выше для рассмотрения дифференциально-геометрических характеристик поверхности вводятся в рассмотрение: касательные направления, касательная плоскость, нормаль к поверхности и
составляется уравнение первой основной квадратичной формы поверхности Д И .
Вторые производные уравнения поверхности Д И . Если дискретно заданная поверхность Д аналити-
чески описана бикубическим уравнением вида (68), то с учетом (71) и (72) имеем
|
|
2r |
д |
|
6U д |
|
||
|
|
|
|
2 0 |
||||
|
U |
2 |
||||||
|
|
|
|
|
|
|||
|
|
д |
|
|
|
|
||
|
|
2r |
д |
|
|
3U д2 |
|
|
|
|
|
|
|
2U д |
|||
U д Vд |
||||||||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
V3 |
||
0 |
|
a q |
|||||
|
ij |
|
|
д |
|
||
q 1 |
|
|
|
|
|
||
|
|
|
|
n |
|
|
|
1 0 |
aijq |
|
|||||
|
|
q 1 |
|
|
|||
Vд2 Vд 1 T ;
3Vд2 2Vд 1 0 T ;
|
2r |
д |
|
|
|
|
|
n |
|
6Vд |
2 0 0 T. |
|
|
|
|
U д3 |
Uд2 |
U д |
1 |
aijq |
|||||
V 2 |
||||||||||||
|
|
|
|
|
q 1 |
|
|
|
||||
|
д |
|
|
|
|
|
|
|
|
|
||
На основании этих формул, по аналогии с рассмотренным выше, для нахождения дифференциально-гео- метрических характеристик поверхности Д И вводится в рассмотрение вторая ее основная квадратичная
форма, которая используется для расчета параметров кривизны поверхности и др.
1.2.5.2. Сложные поверхности деталей и инструментов, заданные числовыми отметками.
Применяемое на практике дискретное задание рабочих поверхностей деталей и инструментов в виде матрицы преимущественно с равномерным распределением элементов (как правило, точек), позволяет при необходи-
мости определить элементы локальной геометрии поверхности Д И , непосредственно исходя из матрицы, определяющей координаты принадлежащих поверхности Д И точек. При решении этой задачи в дискрет-
ной форме появляются особенности.
Необходимые для определения коэффициентов первой Φ1.д и и второй Φ2.д и основных квадратичных форм первые и вторые производные уравнения поверхности Д И , заданной дискретно, могут быть найдены
|
|
1.2. Задание рабочих поверхностей деталей и инструментов. |
|
|
|
|||||||||||
|
|
|
Расчет элементов их локальной геометрии |
|
|
|
75 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
путем использования методов дифференцирования функций, заданных дискретно. |
|
|
|
|||||||||||||
Первые производные поверхности |
Д И . Касательные прямые. В окрестности текущей точки Mi, j на |
|||||||||||||||
поверхности детали или инструмента выбраны две пары |
близлежащих к ней |
точек Mi,( j 1) , Mi,( j 1) , |
||||||||||||||
M i 1 , j , и M i 1 , j |
(рис. 1.15.1), расположенные в двух трансверсальных направлениях |
на Д И . Через три |
||||||||||||||
соседние точки Mi,( j 1) |
, Mi, j |
и Mi,( j 1) |
одного |
ряда |
проходит |
плоскость |
i , |
уравнение которой |
||||||||
представимо в виде (рис. 1.15.2): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
X M X |
i, j |
Y M Y |
Z |
M |
Z |
i, j |
|
|
|
|
||||
|
|
i |
|
|
i |
i, j |
|
i |
|
|
|
|
|
|
||
|
|
Xi, j 1 Xi, j |
Yi, j 1 Yi, j |
Zi, j 1 Zi, j |
0 |
|
|
(1.73) |
||||||||
|
|
Xi, j 1 Xi, j |
Yi, j 1 Yi, j |
Zi, j 1 Zi, j |
|
|
|
|
||||||||
или в векторной форме: |
rк.i ri, j |
ri, j 1 ri, j ri, j 1 ri, j |
0 . |
|
|
|
||||||||||
|
|
|
|
|
||||||||||||
|
Nд u |
|
|
|
rд u |
|
|
|
|
|
|
Nд u |
|
|
rд u |
|
|
Mi 1, j 1 |
i |
|
|
Vд u |
|
|
|
|
|
|
i |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|||
|
|
|
|
Mi, j 1 |
Д И |
|
|
|
|
|
|
д u |
||||
Mi 1, j |
|
|
|
|
|
|
|
|
|
|
||||||
|
Mi, j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Mi, j Mi, j 1 |
|||
|
|
|
|
|
|
|
Mi 1, j 1 |
|
|
|
|
Mi, j 1 |
||||
Mi 1, j 1 |
Mi, j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
rд u |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Zд u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Mi 1, j |
Uд u |
|
|
2. |
|
|
|
|
||||
rд u |
|
|
j |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
Nд u |
|
|||
|
|
Mi 1, j 1 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Y |
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
rд u |
|
д u |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Uд u |
|
|
|
|
|
|
|
|
|
|
|
|
|
Mi 1, j |
Mi, j |
Mi 1, j |
|
|
Xд u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
|
|
|
|
|
|
|
3. |
|
|
|
|
|
Рис. 1.15. Локальный участок дискретно заданной поверхности |
Д И в окрестности точки Мi, j на ней. |
|||||||||||||||
Аналогичные уравнения справедливы и для поскости j , |
проходящей через другие три соседние точки |
|||||||||||||||
M i 1 , j , Mi, j и Mi,( j 1) |
во втором ряду: |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
X |
M X |
|
Y M |
Y |
Z |
M Z |
|
|
|
|
||||
|
|
|
j |
i, j |
|
j |
|
i, j |
|
j |
|
i, j |
|
|
|
|
|
|
X i 1 , j Xi, j |
Yi 1 , j Yi, j |
Z i 1 , j Zi, j 0 |
|
|
|
|||||||||
|
|
X i 1 , j Xi, j |
Yi 1 , j Yi, j |
Z i 1 , j Zi, j |
|
|
|
|||||||||
и в векторной форме: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
76 |
1. Рабочие поверхности деталей и инструментов |
|
|
r к. j ri, j ri, j 1 ri, j ri, j 1 ri, j |
0 . |
Система координат XiYi Zi связана с плоскостью (73) таким образом, что ее начало расположено в плоскости (73), а координатная плоскость XiYi совпадает с этой же плоскостью. Тогда в системе координат XiYi Zi уравнение окружности, проходящей через три точки Mi,( j 1) , Mi, j и Mi,( j 1) , имеет вид:
(1.74) |
Xc.i |
XO,i 2 |
Yc.i |
YO.i 2 |
Ri2 , |
|||||
где Xc.i и Yc.i |
– координаты текущей точки окружности в системе координат XiYi Zi ; |
|||||||||
XO.i и YO.i |
– координаты цетра окружности; |
|
|
|
|
|
|
|
||
Ri |
– радиус окружности. |
|
|
|
|
|
|
|
|
|
Неизвестные параметры окружности XO.i , |
YO.i и Ri |
находятся как решение системы уравнений: |
||||||||
|
|
X |
* X |
O.i |
2 Y* Y |
2 |
R2 ; |
|||
|
|
|
i |
|
i |
O.i |
|
|
i |
|
(1.75) |
|
* |
|
|
|
2 |
* |
|
2 |
2 |
X i 1 XO.i |
Yi 1 YO.i |
Ri ; |
||||||||
|
|
|
|
|
|
2 |
|
|
2 |
|
|
X*i 1 XO.i |
Y*i 1 YO.i Ri2 , |
||||||||
|
|
|
|
|
|
|
|
|
|
|
где X*i 1 , Y*i 1 ; |
Xi* , Yi* и X*i 1 , Y*i 1 – координаты точек Mi,( j 1) , Mi, j |
и Mi,( j 1) |
XiYi .
Исходя из (74) с учетом (75) уравнение касательной к окружности (74) в точке Mi, j столбцовой матрицы:
в системе координат
представимо в виде
|
|
|
|
|
|
X* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
*i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
Y |
|
|
|
* |
|
* |
|
|
T |
|
|
|
|
||
(1.76) |
|
|
|
|
i |
|
|
|
0 |
|
|
|
|
|
||||||||
|
|
|
ri |
|
0 |
|
Xi |
Yi |
1 . |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Перейдя |
от системы |
|
координат |
XiYi |
|
|
к |
исходной |
системе |
координат Xд и Yд и Zд и , в которой |
||||||||||||
поверхность |
Д И задана изначально, |
получим вектор |
|
ri |
касательной |
|
ri* |
(76), записанный в исходной |
||||||||||||||
системе координат Xд и Yд и Zд и : |
|
|
|
|
|
|
|
|
Xi* U |
д и |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Xi U |
д и |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Yi U д и |
|
|||
(1.77) |
r |
|
Res i Д r |
* |
M |
|
|
|
Y* U |
д и |
|
|
||||||||||
i |
i |
i д |
|
i |
|
|
|
|
|
|
. |
|||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Zi U д и |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аналогичное соотношение может быть получено и для другой плоскости (рис. 1.15.3), проходящей через три соседние точки M i 1 , j , Mi, j и Mi,( j 1) :
|
|
|
|
|
|
|
|
X |
* V |
|
|
X j V |
|
|||
|
|
|
|
|
|
|
|
|
|
j |
д и |
|
|
д и |
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
Yj Vд и |
||||
(1.78) |
r |
|
Res i Д r |
* |
M |
|
|
Y* |
|
|||||||
j |
j |
j д |
|
j |
д и |
|
|
|
|
. |
||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Z j Vд и |
||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

1.2. Задание рабочих поверхностей деталей и инструментов.
|
Расчет элементов их локальной геометрии |
77 |
||||
|
|
|
|
|
|
|
Параметрами в уравнениях касательных являются U д и и |
Vд и параметры. В качестве |
U д и и |
||||
Vд и параметров могут быть использованы, например, углы поворота радиус-вектора окружностей в каж- |
||||||
дом из плоских нормальных сечений поверхности Д И . |
|
|
|
|
||
Касательная плоскость к поверхности |
Д И в некоторой ее точке Mi, j находится как плоскость, |
|||||
проходящая через эту точку и содержащая два направления (77) и (78). Поэтому ее уравнение имеет вид: |
||||||
|
XКП Xi, j |
YКП Yi, j |
ZКП Zi, j |
|
|
|
|
|
|
||||
|
li |
mi |
ni |
|
0 . |
|
|
l j |
m j |
n j |
|
|
|
Нормаль к поверхности Д И определяется через векторное произведение касательных. С учетом (77) и (78) в этом случае имеет место соотношение:
|
i |
j |
Nд и |
Xi |
Yi |
|
X j |
YJ |
Для расчета орта нормали справедлива формула:
n д и |
|
Nд и |
|
|
Nд и |
|
|
|
|
||
|
Nд и |
Xi X j 2 Yi Yj 2 Zi Z j 2 |
|||
|
|
|
|
|
k
Zi .
Z j
|
|
|
i |
j |
k |
|
|
|
|
|
|
Xi |
Yi |
Zi |
|
|
|
|
|
|
X j |
Yj |
Z j |
|
|
. |
|
|
|
|
|
||||
|
|
|
|
|
|
|
||
Xi X j |
2 Yi Yj 2 Zi Z j 2 |
|||||||
Первая основная квадратичная форма поверхности Д И определяется уравнением (23), коэффициенты первой основной квадратичной формы Φ1.д и равны соответственно (25).
С учетом (77) и (78) можно записать, что:
Eд и Xi 2 |
Yi 2 |
Zi 2 ; |
(1.79) |
|||
Fд и Xi X j |
Yi Yj Zi |
Z j ; |
(1.80) |
|||
Gд и X j |
2 |
Yj |
2 |
Z j |
2 . |
(1.81) |
Тогда с учетом (79)-(81) первая основная квадратичная форма представима в виде:
Φ1.д и |
dSд2 и Xi 2 Yi 2 Zi 2 |
dUд2 и |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 X |
i |
X |
j |
Y Y Z |
i |
Z |
j |
dU |
dV |
X |
j |
2 Y |
2 |
Z |
2 |
dV 2 . |
|
|
|
i J |
|
|
д и д и |
|
|
j |
|
j |
д и |
|||||
Вторые производные и вторая основная квадратичная форма поверхности Д И . Вторая основная квадратичная форма поверхности Д И определяется как (38), а ее коэффициенты равны (48)-(50) соответственно.
78 1. Рабочие поверхности деталей и инструментов
Для вычисления коэффициентов Lд и , Mд и и Nд и второй основной квадратичной формы Φ2.д и в рассматриваемом случае известны все первые производные от Xд и , Yд и и Zд и по параметрам U д и и Vд и , а также коэффициенты Eд и , Fд и и Gд и первой основной квадратичной формы Φ1.д и (см. выше). Не известными остаются входящие в формулы (48)-(50) вторые производные от Xд и , Yд и и Zд и по параметрам U д и и Vд и . Чтобы отыскать эти производные при дискретном задании поверхности Д И ,
воспользуемся подходом, используемым при выводе формул Вейтгартена (Struik, D.J., 1961).
Уравнения Вейтгартена (или Гаусса-Вейнгартена). Коэффициенты Eд и , Fд и и Gд и первой основ-
ной квадратичной формы |
|
Φ |
|
поверхности |
Д И зависят только |
от первых производных |
|
rд и |
и |
||||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1.д и |
|
|
|
|
|
|
|
|
|
|
|
U д и |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
rд и |
|
, а коэффициенты Lд и , Mд и и Nд и |
второй основной квадратичной формы Φ2.д и зависят как от |
|||||||||||||||||||
|
Vд и |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
первых |
|
rд и |
и |
rд и |
, |
так и от вторых производных |
2rд и |
, |
|
2rд и |
и |
2rд и |
. |
Поэтому |
|||||||||
|
U |
д и |
V |
|
2 |
|
U |
V |
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
д и |
|
|
|
|
U д и |
|
|
|
д и |
д и |
|
Vд и |
|
|
|
||
соотношения между коэффициентами первой и второй основными квадратичными формами не могут быть чисто алгебраическим (чисто алгебраические соотношения имеют место в особых случаях, для характеристики специальных поверхностей или для описания локальной топологии поверхностей в
специальных точках, таких, как омбилические). В общем случае соотношения между коэффициентами Eд и , Fд и , Gд и и Lд и , Mд и , Nд и носят дифференциальный характер и могут быть найдены так.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
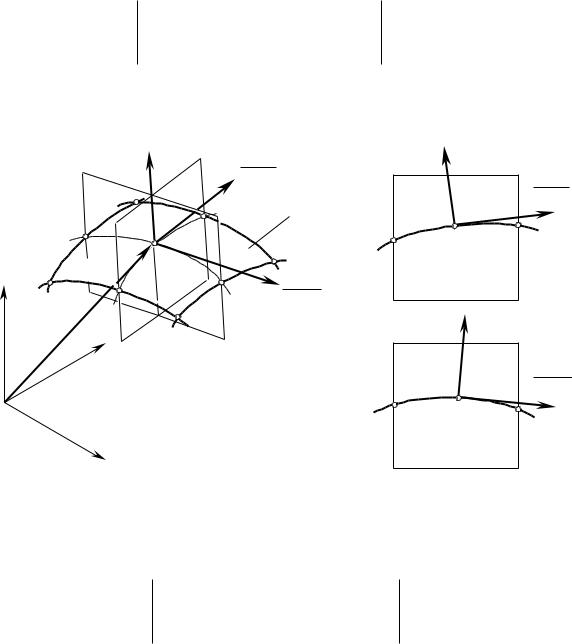
Введем в рассмотрение подвижный трехгран- |
||||||||||||||
|
|
|
|
U д и линия |
n д u |
rд u |
|
|
|
ник (рис. 1.16) |
с началом в текущей точке M на |
|||||||||||||||||||
|
Vд и линия |
|
|
|
|
|
|
|
поверхности |
Д И , |
который образован не тремя |
|||||||||||||||||||
|
|
|
|
|
Vд u |
|
|
|
взаимно перпендикулярными единичными вектора- |
|||||||||||||||||||||
|
|
|
|
|
|
M |
|
|
|
|
|
Д И |
|
ми, а |
|
тремя |
линейно |
независимыми векторами |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
rд и |
|
, |
rд и |
и |
n |
д и . Векторы |
rд и |
и |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Zд u |
|
|
|
|
|
|
|
|
|
|
|
|
|
U д и |
Vд и |
|
|
|
|
U д и |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
rд u |
|
|
|
rд u |
|
|
|
|
rд и |
|
лежат в плоскости, касательной в точке M |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Vд и |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
Uд u |
|
|
|
|
|
|
|
|
Д И , |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
Yд u |
|
|
|
к поверхности |
|
которая в |
свою |
очередь |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ортогональна орту нормали n д и . Этот подвижный |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
трехгранник зависит от двух параметров |
U д и и |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
Xд u |
|
|
|
|
|
|
|
|
Vд и . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Любой вектор может быть линейно выражен |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
через |
составляющие |
подвижного |
трехгранника. |
||||||||||||
Рис. 1.16. Подвижный трехгранник, связанный с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2rд и |
|
||||||||||||||
|
|
|
текущей точкой М на поверхности |
|
Д И . |
|
Если |
выполнить это |
для векторов |
|
|
|
, |
|||||||||||||||||
|
|
|
|
|
U д2 и |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2rд и |
и |
2rд и |
, то получим уравнения следующего вида: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
U |
V |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
д и |
д и |
|
Vд и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2rд и |
|
|
|
rд и |
|
|
rд и |
|
|
|
n |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
U д2 и |
1 U д и |
|
2 Vд и |
|
|
3 |
|
д и |
|
|
|
|
|
|
|
|
||||||

1.2. Задание рабочих поверхностей деталей и инструментов.
|
|
|
|
|
|
|
|
Расчет элементов их локальной геометрии |
|
|
|
|
|
|
|
|
|
|
|
|
79 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2r д и |
|
|
|
|
rд и |
|
|
|
r д и |
|
|
n |
|
|
; |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
U |
|
V |
|
|
1 U |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
д и |
|
|
|
|
|
д и |
|
|
2 V |
|
|
|
|
|
3 |
|
|
д и |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
д и |
|
|
|
|
|
|
|
|
д и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
2rд и |
|
|
r д и |
|
|
rд и |
|
|
n |
|
|
|
|
, |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
V |
2 |
|
|
|
|
1 Uд и |
2 Vд и |
|
|
3 |
|
д и |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
д и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где коэффициенты 1, , 3 должны быть определены. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Используя соотношения (25) для гауссовых коэффициентов |
Eд и , |
|
Fд и , Gд и |
и уравнение (23) для |
||||||||||||||||||||||||||||||||||||||||
первой основной квадратичной формы Φ1.д и , приходим к результату: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
d 2rд и |
n |
|
L ; |
|
|
|
|
|
|
d 2rд и |
n |
|
|
|
M |
|
|
|
; |
|
|
|
|
|
|
d 2r д и |
n |
|
N |
. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
3 |
|
dUд2 и |
д и |
|
д и |
|
|
3 |
|
dUд и dVд и |
|
д и |
|
|
д и |
|
|
|
|
|
3 |
|
dVд2и |
|
д и |
|
д и |
||||||||||||||||
Cнова используя соотношения (25) для гауссовых коэффициентов Eд и , Fд и , Gд и первой основной квадратичной формы Φ1.д и и введя обозначения:
11, 1 d 2rд и drд и ; dUд2 и dUд и
находим, что
11, 1 Eд и 1 Fд и 2 ;
11, 2 d 2rд и drд и , dVд и
11, 2 Fд и 1 Gд и 2
или, решая эти уравнения относительно 1 и 2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
1 |
Gд и 11, 1 Fд и 11, |
2 |
; |
|
2 |
|
Eд и 11, 2 Fд и 11, 1 |
. |
|
|
(1.82) |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
E |
G |
|
|
F |
2 |
|
|
|
|
|
|
|
|
|
|
E |
|
G |
д и |
F |
2 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
д и д и |
|
|
д и |
|
|
|
|
|
|
|
|
|
|
|
|
|
д и |
|
|
|
д и |
|
|
|
|
|
|||||||||||||
Взятые в квадратные скобки символы 11, 1 и |
11, 2 выражаются через производные от |
Eд и , |
Fд и и |
||||||||||||||||||||||||||||||||||||||||
Gд и , поскольку |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
drд и |
|
d 2rд и |
|
|
dEд и |
; |
|
|
2 |
|
drд и |
|
|
|
d |
2rд и |
|
|
|
dEд и |
; |
|
|
|||||||||||||||||||
dUд и |
dUд2 и |
|
dUд и |
|
|
|
dUд и |
|
|
|
dUд и dVд и |
dVд и |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
drд и |
|
|
|
|
d 2rд и |
|
d 2rд и |
|
|
|
drд и |
|
|
dFд и |
. |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
dUд и |
|
dVд и dUд и |
dUд2 и |
|
dVд и |
dUд и |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Поэтому: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
11, 1 |
1 |
|
dEд и |
; |
|
|
|
|
11, 2 |
dFд и |
|
1 |
|
dEд и |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
dUд и |
2 dVд и |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
2 dUд и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
