Добавил:

Mehanik Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Технический Университет им. Р.Е. Алексеева

Предмет:

Технология машиностроения

Файл:

Radzevich, S.P. Monograph - 2001

.pdf

Скачиваний:

Добавлен:

23.02.2023

Размер:

24.47 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 605 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

40	1. Рабочие поверхности деталей и инструментов

Векторы drд и и d Vд и коллинеарные – это следует из уравнения (19), согласно которому направление смещения точки по поверхности Д И зависит только от отношения

д и

(1.20)

д и

dUд и

Величина смещения точки M по длине дуги равна

(1.21)

dSд и

drд и

а первая основная квадратичная форма поверхности

Д И

представляет собой квадрат дифференциала

длины этой дуги

(1.22)

Ф1.д и

dSд2 и drд2 и .

Таким образом, по определению первая основная квадратичная форма Ф1.д и поверхности

Д И есть

квадрат линейного элемента этой поверхности в направлении, определенном относительно поверхности соот-

ношением

dVд и

дифференциалов:

dUд и

д и

1.д и

д и

(1.23)

dUд и 2

д и

dUд и dVд и

dVд и

д и

Eд и dUд2 и 2Fд и dUд и dVд и Gд и dVд2и .

Вобозначениях Гаусса имеем

(1.24)

drд и

rд и

dUд и

rд и

dVд и ;

д и

rд и 2

rд и

rд и 2

Eд и

Gд и

;

Fд и

д и

;

д и

Гауссовы коэффициенты Eд и , Fд и , Gд и первой основной квадратичной формы поверхности Д И представляют собой скалярные функции внутренних координат – функции Uд и и Vд и параметров:

Eд и rд и 2 Uд и , Vд и ;

Uд и


F	д и	rд и		U	, V	rд и	U	, V	;

		U	д и		д и д и	V		д и д и
						д и

1.2. Задание рабочих поверхностей деталей и инструментов. Расчет элементов их локальной геометрии

Gд и rд и 2 Uд и , Vд и .

Vд и

В координатах они соответственно равны:

Eд и

rд и

;

Fд и

rд и

;

Gд и

rд и

д и

(1.25)

Здесь и далее все частные производные вычисляются в одной точке на поверхности Д И , например, в

точке К их касания.

Первая основная квадратичная форма поверхности Д И может быть записана в такой форме (Maekawa, T., Patrikalakis, N., 1994):

rд и

д и

1.д и

д и

Этому соотношению соответствует следующая форма записи коэффициентов первой основной квадратичной формы поверхности Д И и их первых производных (Maekawa, T., Patrikalakis, N., 1994):

Eд и

rд и

;

Eд и

rд и

2rд и

;

Eд и

rд и

2rд и

;

д и

U д и

д и

Fд и

rд и

;

д и

Fд и

2rд и

rд и

2rд и

;

Fд и

2rд и

rд и

2rд и

;

д и

U д и

д и

Vд и

rд и

д и

;

Gд и

rд и

2rд и

;

Gд и

rд и

2rд и

д и

Vд и

Квадрат дискриминанта линейного элемента обозначается так:

д и

H д и Eд и Gд и Fд и

д и

(1.26)

д и

или в координатах

(Yд и , Zд и

(Zд и , Xд и

(Xд и , Yд и

Hд и

0 ;

, V

д и

42	1. Рабочие поверхности деталей и инструментов

Hд и 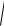Eд и Gд и Fд2и .

Всегда принимается, что Hд и 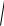Eд и Gд и Fд2и .

Выражение для площади Sд и фрагмента поверхности Д И имеют вид (Ефимов Н.В., 1978):

dX dY

Xд и , Yд и dU

д и

д и д и

д и

, V

д и

(1.27)

Xд и

Uд и

Vд и

F 2 dU

dV .

Yд и

д и

д и д и

д и

Uд и

Vд и

связи с тем,

что

для измерения длин дуг на поверхностях

И , углов между двумя пере-

секающимися кривыми на них и площадей отсеков поверхностей достаточно знать только первую основную

квадратичную форму, говорят, что квадратичная форма Φ1.д и

определяет метрику поверхности

Д И , в

связи с чем называют ее линейным элементом этой поверхности.

x M y M z M ,

Если рассмотрение вести в ортонормированной системе

начало координат

которой

совмещено с точкой

M , оси x M

y M расположены в плоскости,

касательной к поверхности

Д И

точке M , а ось

z M

направлена по нормали к ней (как это имеет место для подвижного репера с базисом

(16)), то вследствие равенства нулю косинусов углов, образованных координатными осями

x M

y M , а

также этими координатными осями с нормалью к поверхности

Д И ,

коэффициенты первой основной

квадратичной формы Φ1.д и приобретают особенно простой вид:

Eд и 1,

Fд и 0,

Gд и 1.

Следовательно,

составленный

из

этих

коэффициентов дискриминант

д и

F 2

д и

рассматриваемом случае будет тождественно равен H д и 1 .

В общем случае величина дискриминанта Hд и рассчитывается как модуль векторного произведения:

(1.28)

Hд и

rд и

д и

Раскрыв первую фундаментальную матрицу (6) или исходя из соотношений (26), получим:

д и

(1.29)

F 2

д и д и

д и

	1.2. Задание рабочих поверхностей деталей и инструментов.	43
	Расчет элементов их локальной геометрии	43
	Расчет элементов их локальной геометрии

Лагранж1 установил для векторов, что

A A e e A e 2 A e A e .

Если применить результат Лагранжа к соотношению (29), получим:

rд и

Hд и

д и

Использование дискриминанта в форме (28) позволяет привести еще одно соотношение, по которому можно определить орт нормали к сложной поверхности Д И :

rд и

n д и

U д и

Vд и

Uд и

Vд и

(1.30)

rд и

F 2

д и

U д и

Vд и

Вторые производные уравнения поверхности Д И при задании ее векторным уравнением, имеют вид:

д и

2 X

д и

2 Z

д и

;

U д2 и

д и

U д2 и

д и

2 X

д и

2 Z

д и

;

д и

2 X

д и

2 Z

д и

V 2

д и

Эти производные используются для определения кривизны поверхности

Д И

и др. параметров ее

локальной топологии – детально они рассматриваются ниже. Здесь кратко остановимся только на разъяснении геометрического смысла вектора перекрестной производной.

Перекрестную производную	2 rд и			часто называют вектором кручения поверхности Д И , т.е.
	U	V

		д и	д и

1Лагранж, Жозеф Луи (25.1.1736 – 10.4.1813) – французский математик и механик, чл. Берлинской АН (1759), Парижской АН (1772), почетный чл. Петербургской АН (1776). Родился в Турине (Италия), высшее образование получил в артиллерийском училище в Турине, еще до окончания которого начал преподавать в нем математику. Мемуар “О способах нахождения наибольших и наименьших величин интегралов” принес ему признание. В 1766 – 1787 Лагранж был президентом Берлинской АН. После открытия Института и Бюро долгот Лагранж становится их членом и в 1792 вместе с П.Лапласом, Г.Монжем и др. разрабатывает метрическую систему мер. В математическом анализе дал формулу остаточного члена ряда Тейлора, формулу конечных приращений и интерполяционную формулу, ввел способ множителей для решения задачи отыскания условных экстремумов. В области дифференциальных уравнений создал теорию особых решений и разработал метод вариации произвольных постоянных. Установил разложение корней уравнений в т.н. ряд Лагранжа. Исходя из общих законов динамики указал две основные формы дифференциальных уравнений движения несвободной системы, которые названы уравнениями Лагранжа 1-го рода, и вывел уравнения в обобщенных координатах – уравнения Лагранжа 2-го рода. Парижская АН 5 раз отмечала деятельность Лагранжа своими премиями.

44		1. Рабочие поверхности деталей и инструментов
мерой изменения вектора	2 rд и		с изменением	Vд и параметра или мерой изменения вектора	2 rд и	с
	U	2			V2

		д и			д и

изменением U д и параметра. Несмотря на то, что термин вектор кручения употребляется ниже, необходимо

указать, что он может ввести в заблуждение. Значение перекрестной производной в текущей точке параметрически заданной поверхности Д И зависит не только от строения самой поверхности, но и от вида ее пара-

метризации – даже на плоскости она может быть не равна нулю. Поэтому геометрическая интерпретация вектора перекрестной производной как вектора кручения поверхности требует осторожности, так как


2		r д и		0
U		V

	д и		д и

не обязательно свидетельствует о закрученности поверхности.

Вторая основная квадратичная форма поверхности Д И . Покажем, что вторая основная квадратичная форма Φ2.д и поверхности Д И (ее вторая дифференциальная форма Гаусса) характеризует отклонение

точки M * на кривой l , принадлежащей поверхности Д И , от касательной плоскости к этой

поверхности (рис. 1.9).

Вектор t является единичным вектором касательной к произвольной кривой l , лежащей на поверхности Д И и проходящей через точку M

на ней. Из некоторой близкой точки M * кривой l проведем перпендикуляр к плоскости КП , касательной к Д И в точке M – он пересечет

касательную плоскость в точке B . Вектор

l* l*n д и

характеризует отклонение точки M * от касатель-

ной плоскости. Здесь l* является алгебраической величиной – она положительна, когда направле-

ние вектора l* совпадает с направлением орта нормали n д и .

Направление единичной нормали (30) к поверхности Д И может быть определено двояко:

	n д u	Д И
l		КП
l	M
	M
Zд u
M		t
rд u
(M	)	M
rд u
		Yд u

Xд u

Рис. 1.9. К определению второй основной квадратичной

формы Ф2.д u поверхности Д И .

r д и

n д и

U д и

Vд и

или

n *д и

Vд и

U д и

r д и

U д и

Vд и

U д и

Очевидно, что единичные

нормали n д и и n *д и

имеют

взаимно

противоположные

направления

( n д и n *д и ). Помним при этом, что нормаль

Nд и (как и орт нормали

n д и ) к поверхности

Д И всегда

направлены от тела детали и от исходного инструментального тела.

1.2. Задание рабочих поверхностей деталей и инструментов.

Расчет элементов их локальной геометрии

Связь между алгебраической величиной l*

и второй основной квадратичной формой Φ2.д и

основана на

следующем:

Обозначим

радиус-векторы

точек

соответственно

д и

rд и U д и

, Vд и

r M* r

д и

M dU

, V

д и

2. Принимая во внимание, что

д и

(M ) , V (M )

m r

д и

(M ) dU

, V (M ) dV

д и

получим

, V M

m r

д и

, V

д и

(1.31)

д и

3. Смещение l*

точки M * от касательной плоскости равно

l* m n д и .

(1.32)

Уравнения (31) и (32) позволяют записать

l* r

д и

M dU

, V

д и

M , V M

д и

4. Разложив эту разность

д и

, V M

д и

M , V M

д и

в ряд Тейлора1 и ограничивая рассмотрение только членами второго порядка малости, получим:

д и

2 r

д и

2 r

д и

dU 2

dV 2

д и

где все производные рассчитываются в точке M .

5. Векторы производных

rд и

лежат в касательной плоскости, поэтому

U д и

rд и

д и

rд и

n д и

0 .

(1.33)

д и

1Тейлор, Брук (Taylor, Brook) (18.8.1685-29.12.1731) – английский математик, член Лондонского королевского общества (с 1712). Родился в Эдмонтоне (Мидлсекс). Окончил Кембриджский университет (1709). Непременный секретарь Лондонского королевского общества (1714-1718). Основные исследования относятся к математическому анализу, механике и баллистике. Исходя из формулы Ньютона, выражающей приращение функции в виде ряда, расположенного по возрастающим степеням приращения независимой переменной, вывел общую теорему о разложении функции в степенной ряд (ряд Тейлора). Нашел правила дифференцирования функции, обратной данной. В учении об особых решениях дифференциальных уравнений предложил новый вид решений. Дал механико-геометрическую формулировку решения дифференциального уравнения малых колебаний струны. Определил центр качания маятника. Изучал полет снарядов, капиллярные явления, вопросы сцепления между жидкостями и твердыми телами. Показал, что среднее сечение свободной поверхности жидкости между двумя вертикальными пластинками, наклоненными одна к другой под малым углом, есть гипербола. В теории колебаний его результаты были развиты Ж.Л.Д’Аламбером и Ж.Л.Лагранжем. Занимался также вопросами оптики, астрономии и философии.

1. Рабочие поверхности деталей и инструментов

6. Из уравнений (32) и (33) следует, что:

rд и

Φ2.д и

(1.34) l

n д и dU д и

n д и dUд и dVд и

n д и dVд и

д и

Поэтому вторая основная квадратичная форма Φ2.д и

поверхности

Д И равна

удвоенной

величине

отклонения l* .

Если в уравнение (34) ввести обозначения:

2rд и

rд и

r д и

Lд и

2rд и

n д и

U д2 и

U д и

Vд и

;

U д2 и

Eд и Gд и Fд2и

2rд и

r д и

rд и

д и

Mд и

д и

;

д и

Eд и Gд и Fд и

2r д и

r д и

д и

n д и

Vд и

д и

Nд и

Vд2и

Eд и Gд и Fд2и

будем иметь:

2.д и

д и

Коэффициенты Lд и ,

Mд и

Nд и

второй основной

квадратичной

формы

Φ2.д и

могут

быть

использованы для расчета смешанного произведения векторов касательных и кручения поверхности

Д И :

r д и

2r д и

r д и

2r д и

;

д и

U д и

Vд и

U д и

Vд и

U 2

д и

д и д и

д и

r д и

д и

2r д и

r д и

2r д и

д и

H д и n д и U

д и Mд и ;

д и

r д и

2r д и

r д и

2r д и

д и

U д и

Vд и

U д и

Vд и

д и д и

V 2

д и

д и д и

д и

1.2. Задание рабочих поверхностей деталей и инструментов.
Расчет элементов их локальной геометрии	47
	47

Здесь дискриминант равен H д и 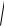Eд и Gд и Fд2и .

По определению вторая основная квадратичная форма поверхности Д И есть проекция на направление нормали n д и перемещения конца бесконечно малого вектора касательной dr д и :

r д и

N д и

2.д и

d r

д и

dU 2

dV2

;

д и

2.д и

d r

д и

d n

д и

d 2

д и

(1.35)

д и

Равенство скалярных произведений

d 2r д и n д и d rд и d n д и

(1.36)

следует из соотношения

d rд и n д и 0

(1.37)

после его дифференцирования.

Уравнение (37) основано на том, что:

Д И из заданной точки M к

а) вектор d r д и описывает бесконечно малое перемещение по поверхности

бесконечно близкой ей точке M * ;

Д И в некоторой ее точке M и поэтому перпендикулярен орту

б) вектор d r д и касателен к поверхности

нормали n д и в этой же точке M . Из уравнения (37) получим

d d r д и n д и d 2rд и n д и drд и dn д и 0 ,

откуда следует (36).

В развернутом виде уравнение Ф2.д и d 2r д и n д и может быть получено так. Дифференцирование (37) дает:

д и

2r д и

dV 2

r д и

д и

r д и

;

д и

U д и

д и

Vд и

д и

Φ2.д и drд и dn д и d 2rд и n д и

(1.38)

1. Рабочие поверхности деталей и инструментов

r д и

dV 2

д и

dV 2

д и

Пользуясь этими соотношениями, следует помнить о порядке выполнения операций векторного и скалярного произведений: в смешанном произведении векторы сначала перемножаются векторно, после чего – скалярно.

Правая часть уравнения (38) представляет собой квадратичную форму дифференциалов dU д и и dVд и . Уравнение (38) может быть получено из равенства

(1.39)

Ф2.д и dn д и dr д и .

После дифференцирования (39) получим

(1.40)

д и

n д и

д и

n д и

dV .

д и

Принимая во внимание уравнения (24), (39) и (40), имеем

n д и

r д и

(1.41)

2.д и

д и

U д и

n д и

r д и

n д и

r д и

n д и

r д и

д и

Vд и

U д и

Vд и

U д и

Vд и

д и

Vд и

д и

С учетом того, что векторы

r д и

rд и

касательны к поверхности Д(И), правую часть уравнения

U д и

Vд и

(41) можно упростить

(1.42)

n д и

rд и

n д и

rд и

д и

Продифференцировав равенства (42) один раз по U д и , другой – по Vд и , получим

д и

n д и

r д и

2r д и

n д и

д и

U д и

д и

r д и

д и

r д и

2r д и

n д и

д и

(1.43)

1.2. Задание рабочих поверхностей деталей и инструментов.

Расчет элементов их локальной геометрии

r д и

n д и

r д и

2r д и

n д и

д и

r д и

n д и

r д и

2r д и

д и

n д и

д и

Vд и

откуда следует, что

r д и

n д и

r д и

n д и

2r д и

д и

Для коэффициентов второй основной квадратичной формы Φ2.д и имеем:

rд и

n д и

д и

2 rд и

;

Uд и

U д и

д и

Mд и

rд и

n д и

rд и

n д и

д и

2 rд и

;

д и

Nд и

rд и

n д и

2 rд и

д и

Уравнение (41) совместно с (43) приводит к результату (38).

Как и для первой основной квадратичной формы

Φ1.д и , гауссовы коэффициенты

Lд и ,

Mд и ,

Nд и

второй основной квадратичной формы Φ2.д и

являются скалярными функциями внутренних координат –

функциями параметров U д и и Vд и :

Lд и Lд и U д и , Vд и ;

Mд и Mд и Uд и , Vд и ;

Nд и Nд и U д и , Vд и .

Параметрически

заданная

поверхность

Д И

общего вида может быть определена как векторное

отображение

двухпараметрического

UV пространства

трехмерное

пространство

(Maekawa, T., and

Patrikalakis, N., 1994):

д и

2.д и

d r

д и

dU 2

д и

dV 2 .

д и

Этому соотношению соответствует краткая форма записи коэффициентов второй основной квадратичной формы поверхности Д И (Maekawa, T., and Patrikalakis, N., 1994):

<<< < Предыдущая 1 2 3 45 / 605 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете Технология машиностроения

#
23.02.202324.47 Mб11Radzevich, S.P. Monograph - 2001.pdf
#
23.02.20237.23 Mб4Горбацевич - Курсовое проектирование по ТМ.doc
#
23.02.2023949.47 Кб3Мешкова - Организация Технологии Отрасли.pdf
#
23.02.20234.4 Mб1Оптимизация Технологических Систем (укр).pdf
#
23.02.2023882.47 Кб3Основные Положения Теории Базирования (Лекции).pdf
#
23.02.20231.01 Mб6Основы Проектирования ТП.pdf