Добавил:

Mehanik Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Технический Университет им. Р.Е. Алексеева

Предмет:

Технология машиностроения

Файл:

Radzevich, S.P. Monograph - 2001

.pdf

Скачиваний:

Добавлен:

23.02.2023

Размер:

24.47 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 609 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

1. Рабочие поверхности деталей и инструментов

и, если подставить эти выражения в (82), видно, что коэффициенты 1 и 2 могут быть определены через Eд и , Fд и и Gд и и их первые производные. Аналогичное справедливо и в отношении коэффициентов

1, 2 и 1, 2 .

Введем новые обозначения для коэффициентов 1 и 2 : обозначим их через 111 и 112 соответственно. Если подобным образом изменить обозначения для коэффициентов 1, 2 и 1, 2 , то придем к системе уравнений:

(1.83)

(1.84)

(1.85)

где коэффициенты ijk

2rд и

rд и

2 rд и

Lд и n д и ;

Uд2 и

Uд и

Vд и

2rд и

rд и

д и

;

12 U

д и

12 V

д и

2rд и

rд и

2 rд и

Nд и n д и ,

Uд и

Vд и

д и

i, j, k 1, 2

определены следующим образом:

Gд и

dEд и

2Fд и

dFд и

Fд и

dEд и

dUд и

dVд и

dUд и

;

2 Eд и Gд и Fд2и

Gд и

dEд и

Fд и

dGд и

dVд и

dUд и

2 Eд и Gд и Fд2и

;

2Gд и

dFд и

Gд и

dGд и

Fд и

dGд и

dVд и

;

dUд и

dVд и

2 Eд и Gд и Fд2и

2Eд и

dFд и

Eд и

dEд и

Fд и

dEд и

dUд и

;

dVд и

2 Eд и Gд и Fд2и

Eд и

dGд и

Fд и

dEд и

dUд и

dVд и

2 Eд и Gд и Fд2и

;

dGд и

dFд и

dGд и

д и

dVд и

д и

dVд и

dUд и

2 Eд и Gд и Fд2и

1.2. Задание рабочих поверхностей деталей и инструментов.

Расчет элементов их локальной геометрии		81
		81
В уравнениях (83)-(85) неизвестными остаются гауссовы коэффициенты Lд и ,	Mд и и	Nд и второй
основной квадратичной формы Φ2.д и поверхности Д И .

Коэффициенты ijk называют символами Кристоффеля. Здесь удобно ввести в рассмотрение не только символы ijk , но и символы kji , определив их как ijk kji , (поскольку 211 121 и 212 122 ).

Выражения ij, k называют символами Кристоффеля первого рода; в этом случае коэффициенты ijk называют символами Кристоффеля второго рода. Они зависят только от коэффициентов Eд и , Fд и и Gд и первой основной квадратичной формы Φ1.д и и их первых производных по параметрам Uд и и Vд и .

Уравнения Гаусса (83)-(85) полезно дополнить двумя уравнениями, которые выражают производные

dn д и	и	dn д и	через их проекции на оси подвижного трехгранника. Поскольку	dn д и	и	dn д и	лежат в
dUд и		dVд и		dUд и		dVд и

касательной плоскости, выражения для их расчета могут быть представлены в таком виде:

dn д и

drд и

;

dn д и

drд и

dUд и

2 dVд и

dVд и

1 dUд и

2 dVд и

Вновь используя соотношения (25) для гауссовых коэффициентов Eд и , Fд и , Gд и первой основной квадратичной формы Φ1.д и и уравнение (23), получаем:

Lд и p1Eд и p2 Fд и ;	Mд и q1Eд и q2 Fд и ;
Mд и p1Fд и p2Gд и ;	Nд и q1Fд и q2Gд и ,

или

dn д и Fд и Mд и Gд и Lд и dUд и Eд и Gд и Fд2и

dn д и Fд и Nд и Gд и Mд и dVд и Eд и Gд и Fд2и

drд и Fд и Lд и Eд и Mд и dUд и Eд и Gд и Fд2и

drд и Fд и Mд и Eд и Nд и dUд и Eд и Gд и Fд2и

drд и ;

dVд и

drд и .

dVд и

Эти уравнения называют уравнениями Вейнгартена.

Зная уравнения (77) и (78) касательных к поверхности Д И , находим уравнение нормали

(1.86)

(1.87)

n д и к ней,

производные	dn д и	и	dn д и	по параметрам Uд и и Vд и , а также величину угла д и между касательны-
производные	dUд и	и	dVд и
	dUд и		dVд и
ми. Это дает возможность дополнить систему из двух уравнений (86) и (87) третьим уравнением
				cos д и	Fд и	(1.88)

					Eд и Gд и
					Eд и Gд и

и таким путем получить полностью определенную систему из трех уравнений (87)-(88) для нахождения трех искомых коэффициентов Lд и , Mд и и Nд и .

Вернемся к рассмотрению вопроса о нахождении производных для функций, заданных дискретно.

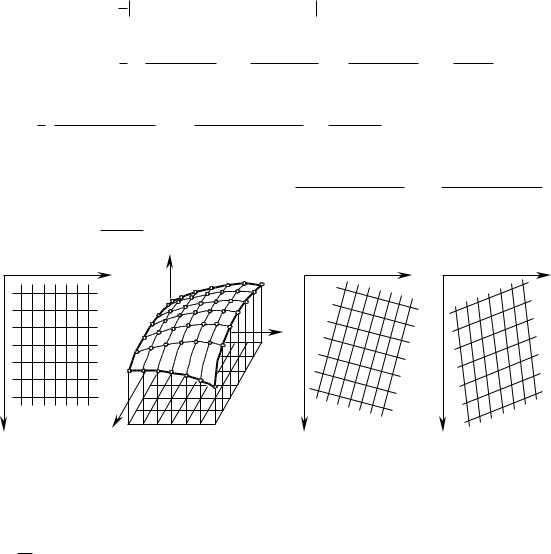
Дифференцирование таблично заданной функции z z x (рис. 1.17) производится по формулам:

1. Рабочие поверхности деталей и инструментов

Z X0

ph 3

p 0,5 Z 1 2 pZ0

p 0,5 Z 1 ;

Z X0

ph 4

3 p

2 6 p 2

Z 1

3 p2 4 p 1

3 p2 2 p 2

Z 1

3 p2

Z 2

;

Z X0

ph 5

2 p3 3 p2 p 1

Z 2

4 p3

3 p2 8 p 4

2 p

3 5 p

Z 1

(1.89)

4 p

3 p

8 p

4 Z

2 p

3 p

1 Z

В этих формулах p X X0

и X X0 ph .

Рис. 1.17. Касательные прямые и дифференцирование поверхностей, заданных числовыми отметками.

Пример 1.4. Найти производную Z X в точке X 0,51 функции Z X , заданной при X0 0,5 и h 0,02 пятью значениями:

Z 2 0,35889029 , Z 1 0,35553253 , Z0 0,35206533 , Z 1 0,34849251 и Z 2 0,344818 . Подставив приведенные исходные данные в

(89), получим: Z 0,51 0,1786491875 .

Для определения производных используются соответствующие зависимости, а именно:

Z	Z 1 Z 1	;	2 Z	Z 1 2Z0 Z 1
X			X 2	h2
	2h

– когда число узлов равно трем;

	Z		Z 2 8Z 1 8Z 1 Z 2	;
	X
			12h
2 Z		Z 2 16Z 1 30Z0 16Z 1 Z 2			;
X2
			12h2

1.2. Задание рабочих поверхностей деталей и инструментов.

Расчет элементов их локальной геометрии			83

	3Z	Z 2 2Z 1 2Z 1 Z 2	;
	X3	2h3

– когда число узлов равно пяти и

Z Z 3 9Z 2 45Z 1 45Z 1 9Z 2 Z 3

60h

Z 2Z 3 27Z 2 270Z 1 490Z0 270Z 1 27Z 2 2Z 3 ; 180h2

Z Z 3 8Z 2 13Z 1 13Z 1 8Z 2 Z 3

8h3

– когда число узлов равно семи.

Формулы для нахождения производных в узлах Z X существенно проще приведенных выше, так как в узлах P X принимает фиксированные значения. Особенно простыми являются формулы для центрального узла P X 0 . Эти формулы удобны для дифференцирования таблично заданных функций в точке X X0 .

Частные производные функции ряда переменных Z X1, X2 , , Xn вычисляются по приведенным выше

формулам, если задавать приращение одной из переменных и оставлять неизменными (равными заданным значениям) остальные переменные.

Для полного решения задачи нахождения производных дополнительно производится анализ чувствительности функции Z X1, X2 , , Xn к изменению ее параметров X1, X2 , , Xn .

Один из простейших способов нахождения смешанных производных уравнения r д и r д и U д и ,Vд и

состоит в следующем.

Уравнение поверхности Д И рассматривается первоначально в неявной форме:

AX 2 BY2 C Z 2 D XY E XZ F YZ G X H Y L Z M 0 ,

после чего его преобразуют к виду:

									X		2			B		Y		2				C				Z		2		D		XY				E			XZ			F			YZ				G			X			H			Y		L		Z			M		0
									X					A		Y							A			Z				A		XY				A			XZ			A			YZ					A		X			A			Y		A		Z			A		0
														A									A							A						A						A								A					A					A					A
и записывают в исходной форме:
									X			2 a Y2 a													2		Z 2		a		3	XY a					4		XZ a				5		YZ a						6	X a				7	Y a			8	Z a				9	0 .
															1										2						3						4						5								6					7				8					9
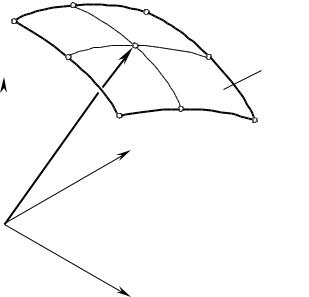
	В окрестности точки															M0,0								(рис. 1.18) на поверхности																							Д И						рассматриваем ближайшие к ней точки
Mi, j		(здесь i 1, 0, 1 и													j 1, 0, 1 ), координаты которых известны (заданы или могут быть расчитаны).
	Координаты этих точек Mi, j																									подставляем в исходное уравнение и таким путем приходим к системе из
X	2		a Y2			a			2	Z		2			a				3		X							Y				a		4	X		1, 1			Z	1, 1					a			Y					Z		1, 1
	1, 1		1	1, 1					2			1, 1							3				1, 1						1, 1					4			1, 1				1, 1							5			1, 1					1, 1
																																																					a6 X 1, 1 a7Y 1, 1 a8 Z 1, 1 a9 0;
X	2	a Y		2	a		2	Z		2			a			3	X			1,0				Y					a		4	X	1,0			Z		1,0		a		5		Y			Z			1,0			a		6		X		1,0	a			7	Y			a	8	Z	1,0	a	9	0;
	1,0		1 1,0				2			1,0						3				1,0						1,0					4		1,0					1,0				5			1,0					1,0					6				1,0				7		1,0			8		1,0		9

1. Рабочие поверхности деталей и инструментов

84
X	2		a Y2					a				2	Z		2				a				3			X		Y						a			4	X			1, 1					Z		1, 1			a		5			Y					Z	1, 1
	1, 1			1	1, 1							2			1, 1								3				1, 1		1, 1								4				1, 1							1, 1					5				1, 1					1, 1
																																																												a6 X 1, 1 a7Y 1, 1 a8 Z 1, 1 a9 0;
X	2	a Y			2		a			2	Z		2			a				3		X					Y			a			4	X		0, 1				Z			0, 1				a			Y				Z			0, 1			a			6		X		0, 1			a					Y			a		8	Z		0, 1		a		9	0;
	0, 1		1 0, 1							2			0, 1							3					0, 1 0, 1								4			0, 1							0, 1							5 0, 1							0, 1						6				0, 1							7 0, 1						8			0, 1				9
X	2 a Y2					a		2	Z		2			a			3	X			0,0			Y				a	4	X	0,0			Z	0,0				a					5	Y Z					0,0	a				6		X	0,0			a				7	Y a							8		Z	0,0	a		9	0;
	0,0		1	0,0				2			0,0						3				0,0					0,0			4		0,0				0,0									5	0,0					0,0					6			0,0							7		0,0						8			0,0			9
X	2	a Y			2		a			2	Z		2			a				3		X					Y			a			4	X		0, 1				Z			0, 1				a			Y				Z			0, 1			a			6		X		0, 1			a					Y			a		8	Z		0, 1		a		9	0;
	0, 1		1 0, 1							2			0, 1							3					0, 1 0, 1								4			0, 1							0, 1							5 0, 1							0, 1						6				0, 1							7 0, 1						8			0, 1				9
X	2		a Y2					a				2	Z		2				a				3			X		Y						a			4	X			1, 1					Z		1, 1			a		5			Y					Z	1, 1
	1, 1			1	1, 1							2			1, 1								3				1, 1		1, 1								4				1, 1							1, 1					5				1, 1					1, 1
																																																												a6 X 1, 1 a7Y 1, 1 a8 Z 1, 1 a9 0;
X	2	a Y2					a			2	Z		2			a			3			X					Y			a		4		X	1,0				Z			1,0				a			Y			Z				1,0			a			6		X		1,0			a				Y				a		8	Z		1,0		a		9	0;
	1,0		1 1,0							2			1,0						3					1,0				1,0				4			1,0							1,0							5 1,0							1,0						6				1,0						7			1,0				8			1,0				9
X	2		a Y2					a				2	Z		2				a				3			X		Y						a			4	X			1, 1					Z		1, 1			a		5			Y			1		Z	1, 1						a		6	X				1, 1		a		7	Y
	1, 1			1	1, 1							2			1, 1								3				1, 1		1, 1								4				1, 1							1, 1					5				1,		1			1, 1								6					1, 1				7		1, 1

a8 Z 1, 1 a9 0

девяти линейных уравнений для нахождения девяти неизвестных коэффициентов a1 , a2 , …, a9 .

M 1,0

Найденные путем решения этой системы

M 1, 1

коэффициенты a1 , a2 , …, a9

подставляются в

исходное уравнение, которое затем пребразуется

M0, 1

M0,0

(для этого используются методы, рассмотренные

M0, 1

ниже, в гл. 3) к виду r д и r д и U д и ,Vд и .

Д И

В результате появляется возможность нахо-

Zд u

дить смешанные и все другие необходимые

производные, причем не только в узловых точ-

rд u

M 1, 1

M 1,0

M 1, 1

ках Mi, j , но и в промежуточных между ними, в

том числе и за пределами отсека поверхности,

ограниченного

дугами

M 1, 1M 1,0 M 1, 1 ,

Y u

1, 1

0, 1

1, 1

1,0

1, 1

M 1, 1M0, 1M 1, 1 . В последнем случае к

результатам

нахождения

всех

производных

следует относиться с некоторой долей осторож-

ности – чем дальше от центра интерполирования

Xд u

M0,0

расположена точка,

в которой требуется

расчитать производные, тем больше погрешно-

сти расчетов.

Рис. 1.18. К нахождению смешанных производных

Как видно из изложенного, рассмотренный

подход к нахождению смешанных производных

дискретно заданной поверхности Д И .

уравнения поверхности

Д И

предельно прост

– для более точных расчетов могут быть использованы более совершенные (и вместе с тем, как правило, более громоздкие) методы нахождения смешанных производных.

1.2.6. Задание сложных поверхностей Д(И) с учетом допусков на точность их размеров и формы.

При формообразовании поверхностей деталей режущими инструментами неизбежны погрешности

1.2. Задание рабочих поверхностей деталей и инструментов.
Расчет элементов их локальной геометрии	85
	85

технологической системы. Поэтому номинальные значения параметров обработанной поверхности задают с допусками. В связи с этим появляется некоторая неоднозначность в задании поверхности Д . Чтобы исклю-

чить такую неоднозначность и обеспечить однозначность в задании поверхности детали, необходимую для последующего расчета инструмента, вводят в рассмотрение так называемую расчетную поверхность, которую обычно располагают в поле допуска на поверхность Д детали и рассматривают ее как расчетную поверх-

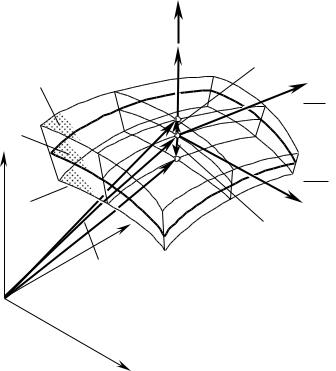
ность (рис. 1.19).

Рассмотренные выше методы задания и аналитического описания поверхностей деталей и инструментов позволяют ввести в рассмотрение аналитическое представление поверхности Д И с учетом допусков на точ-

ность их размеров и формы.

Реальные поверхности Д И всегда имеют отклонения размеров и параметров формы от их номи-

нальных значений, заданных чертежом детали и инструмента. Приемлемые величины отклонений регламентируются допусками на точность каждого из параметров. Результирующая погрешность обработки

h не должна превышать величину допуска hд на точность обработки (h hд ).

Наряду с номинальными поверхностями Дн

будем рассматривать поверхности

Д ..нв

и И ..нв ,

отстоящие

от

номинальных

поверхностей Д И

на

величины

верхних д.в, и.в

и нижних

д.н, и.н

предельных отклонений для поверх-

Nд

ностей Д и И соответственно. Ана-

литическое

описание

поверхностей

в.д U

предельных отклонений рассмотрим на

n д

примере

поверхностей

Д .в

.н

(рис. 1.19), после чего распространим

rд

полученный результат на поверхности

Дн

Vд

предельных отклонений

И .в

и И .н

исходной

инструментальной

поверх-

Zд

ности.

rд

В наиболее простом случае одно

rд. n

из предельных отклонений рассматри-

Uд

вается

равным нулю

( д.в

или

д.н 0 ).

Тогда

допуск на

точность

н.д

обработки будет равен значению того

Yд

предельного отклонения, которое не

rд

равно

нулю:

hд д.н

или

h д.в .

В более общем случае оба

предельных отклонения не равны ну-

Xд

лю: д.в

д.н

0 , в том числе они

могут

иметь

противоположные

знаки

(противоположные направления отсче-

Рис. 1.19. Поверхность

Д детали и поверхности Д В верхнего

та), а также быть равными по модулю.

Поверхность допуска Д h (в пер-

Д Н нижнего предельных отклонений.

вом случае) и поверхности верхнего Д .в и нижнего Д .н предельных отклонений (во втором случае) будут эквидистантными (параллель-

ными) номинальной поверхности Д детали.

Как правило каждая поверхность детали обрабатывается одним технологическим методом. Поэтому естественно предположить, что в виду постоянства условий обработки величины верхнего и нижнего предельных отклонений должны быть постоянными по величине – именно это имеет место при обработке большинства деталей общемашиностроительного назначения. При обработке деталей с рабочими поверх-

1. Рабочие поверхности деталей и инструментов

ностями сложной формы, когда имеет место изменение в большом диапазоне кривизны обрабатываемой поверхности, условия взаимодействия инструмента с деталью в пределах обрабатываемой поверхности Д

переменны. Это оказывает влияние на точность обработки и игнорировать это влияние можно не всегда. Поэтому допуск на точность обработки сложной поверхности детали может быть переменным в пределах обрабатываемого участка ее поверхности: в наиболее общем случае переменные величины предельных отклонений для всей обрабатываемой поверхности детали можно рассматривать как функции гауссовых координат на Д , т.е.

д.в д.в U	д	,V ;		д.н		д.н	U	д	,V	.
	д	д		д.н		д.н		д	д

Допуск на точность обработки, верхние и нижние предельные отклонения отсчитываются от номинальной поверхности Д по нормали к ней.

Исходим из того, что номинальная поверхность Д аналитически описана уравнением в векторной форме: rд rд(Uд,Vд) , а орт нормали к поверхности Д будет:

		rд	rд
n	д	Uд	Vд	.
		Uд	Vд

		rд	rд
		rд	rд
		Uд	Vд
		Uд	Vд

Векторные уравнения поверхности допуска и поверхностей верхнего и нижнего предельных отклонений для детали представимы в виде

(1.90)	rд[h] rд		n д hд (Uд,Vд) ;
(1.91)	r д.в r	д	n	д	д.в(U	д	,V ) ;
		д		д		д	д
(1.92)	rд.н rд n д д.н(Uд,Vд)
соответственно.	В эти уравнения подставляются алгебраические значения параметров							[h ] ,	в.д(U	д	,V )
								д		д	д

и н.д(Uд,Vд) , т.е. взятые с учетом их знака.

Каждое из приведенных трех уравнений может быть записано в проекциях на координатные оси, например, так:

rд[h] rд.x nд.x[hд](Uд,Vд) iд rд.y nд.y[hд](Uд,Vд) jд rд.z nд.z[hд](Uд,Vд) k д.в

(1.93) r д.в rд.x nд.x д.в (Uд,Vд) i д rд.y nд.y д.в (Uд,Vд) jд rд.z nд.z д.в (Uд,Vд) k д.в ;

r д.н rд.x nд.x д.н (U д,Vд) i д rд.y nд.y д.н ](U д,Vд ) jд rд.z nд.z д.н (U д,Vд) k д.в

или соответственно в параметрической форме.

Очевидно, что изложенное справедливо и в отношение исходной инструментальной поверхности И . Поэтому по аналогии с (90), (91) и (92) сразу запишем векторные уравнения поверхностей допуска и поверхностей верхнего и нижнего предельных отклонений для инструмента:

(1.94)

rи[h] r и n и hи (Uи ,Vи ) ;

1.3. О классификации рабочих поверхностей деталей и инструментов							87

r и.в r	и	n	и	и.в(U	и	,V ) ;	(1.95)
						и
rи.н rи		n и		и.н(Uи,Vи) .			(1.96)

Для инструмента уравнения, аналогичные (93), записываются так:

rи[h] rи.x nи.x[hи](Uи,Vи) iи rи.y nи.y[hи](Uи,Vи) jи rи.z nи.z[hи](Uи,Vи) k и.в ;

и.в r

и.в

,V ) i

и.в

,V ) j

n и.в

,V ) k

и.в

;

и.x

и.y

и.z

rи.н rи.x nи.x и.н(Uи,Vи) iи rи.y nи.y и.н](Uи,Vи) jи rи.z nи.z и.н(Uи,Vи) k и.в .

Уравнения (94), (95) и (96), а также соответствующие им формы записи в проекциях на координатные оси (93) или в параметрическом виде используются при расчете производительности многокоординатного формообразования сложных поверхностей деталей на станках с ЧПУ и при решении других задач синтеза.

1.3. О классификации рабочих поверхностей деталей и инструментов

Многообразие форм обрабатываемых поверхностей деталей и типоразмеров применяемых для этих целей фасонных инструментов огромно. Это приводит к большому разнообразию в технологии формообразующей обработки деталей. Для решения задачи синтеза наивыгоднейшего варианта технологии многокоординатной обработки сложных поверхностей деталей на станках с ЧПУ необходима подробная научная

классификация поверхностей Д И , включающая в себя все возможные виды этих поверхностей, опреде-

ленным образом стратифицированных.

1.3.1. Необходимость разработки классификации поверхностей деталей и инструментов.

Геометрическая классификация поверхностей деталей и инструментов, учитывающая требования технологии изготовления деталей, необходима для систематизации известных способов формообразования поверхностей

при механической обработке деталей, упрощения исследования сложных поверхностей Д И и изучения их

геометрической структуры с целью разработки новых высокоэффективных способов формообразования – с тем, чтобы уметь точно и с минимальными затратами времени и средств обрабатывать любую поверхность детали.

Известны многократные попытки классифицировать поверхности технических форм, сгруппировать разнообразные детали по определенным признакам в однотипные семейства для нормализации и типизации технологических процессов их изготовления. Вместе с тем не охваченное единой классификацией их разнообразие сохраняется большим – это приводит к серьезным затруднениям при проектировании, выборе и назначении рациональных видов оборудования, к тому, что многие задачи технологии машиностроения решаются эмпирическим путем.

Поиски принципов для разработки научных основ технологии машиностроения сопряжены с рядом затруднений. Избежать по крайней мере одного из серьезных затруднений, вызванных разнообразием видов изготавливаемых деталей и типов обрабатываемых их рабочих поверхностей, представляется возможным, если использовать формализованный подход к анализу и систематизации форм технических поверхностей, поскольку огромнейшее разнообразие видов изготовляемых деталей сводится к разнообразию форм их рабочих поверхностей.

С уверенностью можно утверждать, что в настоящее время нет научной классификации поверхностей технических форм, в полной мере удовлетворяющей потребностям теории формообразования поверхностей при механической обработке деталей, технологии машиностроения и смежных технических дисциплин. Это

следствие большой сложности задачи разработки научной классификации поверхностей Д И . Установлено

(Фролов С.А., 1983), что в обозримом будущем трудно ожидать возможности решения проблемы разработки классификации поверхностей не только вообще, но и классификации в более узком смысле – классификации

поверхностей технических форм. В этой связи подчеркивается, что многообразие поверхностей Д И и

1. Рабочие поверхности деталей и инструментов

способов их получения не позволяет создать строгую систему для классификации как поверхностей вообще, так и поверхностей Д И в частности. С геометрической точки зрения классификация поверхностей в целом

(как единого геометрического образа) не может иметь научного обоснования. Опыт убедительно показал бесплодность попыток создать научную классификацию поверхностей деталей и инструментов на макроуровне – как единых геометрических образов, которая для технических приложений является более предпочтительной.

Сложившееся положение с разработкой классификации поверхностей технических форм вынуждает изменить уровень рассмотрения этой проблемы, а именно: вместо систематизации поверхностей Д И в

целом как таковых (глобальный подход) классифицировать возможные виды их локальных участков

(локальный подход).

Правомерность локального подхода к вопросу разработки классификации поверхностей Д И оправдывается, в частности, следующим постулируемым положением:

Постулат 1.1. Если при обработке детали обеспечить выполнение всех условий формообразования поверхностей резанием в каждой точке обрабатываемой поверхности Д , то тем самым указанные условия

формообразования могут быть выполнены и для всей обрабатываемой поверхности детали; если хотя бы в одной точке обрабатываемой поверхности детали одно из условий формообразования поверхностей не выполняется, то в этом случае обработать деталь в полном соответствии с требованиями чертежа нельзя.

Первая часть постулированного положения является только необходимой, но не достаточной для обеспечения возможности обработки поверхности детали в полном соответствии с требованиями чертежа, тогда как вторая является достаточной для того, чтобы точно изготовить деталь было нельзя.

Сложные поверхности деталей не допускают движения “самих по себе” – это предопределяет целесообразность локального подхода к их формообразованию, а именно – в дифференциальной окрестности текущей точки на Д и, в этой связи, предполагает широкое использование результатов, полученных в

дифференциальной геометрии поверхностей (Радзевич С.П., 1991). Это также свидетельствует в пользу развития локального подхода к разработке классификации поверхностей деталей и инструментов.

При локальном подходе классификация может быть основана на анализе внутренних свойств и локальной топологии поверхностей Д И .

1.3.2. Круговые диаграммы локальных участков поверхностей деталей и инструментов. Для анализа, наглядной графической интерпретации свойств и разработки классификации гладких регулярных локальных участков поверхностей Д деталей и исходных инструментальных поверхностей И целесообразно

примененить круговые диаграммы (круги Мора1). Уравнение круговых диаграмм локальных участков поверхностей Д И могут быть получены так.

Следуя Nutbourn A. A. (1984) и Nutbourn A. A., Martin R. (1988) при рассмотрении круговых диаграмм локальных участков гладкой регулярной поверхности Д(И) исходим из формулы Эйлера2

(1.97)	k	д и	k	cos2 k	2.д и	sin 2
		д и	1.д и		2.д и

1Мор, Христианн Отто (Mohr, Christian Otto ) (8.10.1835-2.10.1918) – немецкий ученый в области механики. Родился в Вессельбурне (Гольштейн). Окончил Политехническую школу в Ганновере (1855). В 1856-1866 работал инженером железных дорог, в 1867-1873 – профессор Штуттгартского, в 1873-1899 Дрезденского политехнических институтов. С 1900 – в отставке. Одним из первых получил степень инженера-доктора honoris causa . Один из основоположников графической кинематики. Развивал методы графостатики. Предложил графический метод построения упругой линии в простых и неразрезных балках. Разработал метод расчета неразрезных балок с помощью уравнения трех моментов. Создал теорию прочности (теория Мора), разработал графический метод определения напряжений при сложном напряженном состоянии (круг Мора). Впервые применил расчет конструкций на невыгодное нагружение с помощью линий влияния, создал теорию расчета статически неопределимых систем методом сил. Дал обобщение формулы Максвелла (формула МораМаксвелла).

2Эйлер, Леонард (Euler , Leonhard) [4(15). 4.1707, Базель, Швейцария, – 7(18) 9.1783, Петербург], Математик, механик и физик. Родился в семье небогатого пастора Пауля Эйлера. Работал во многих отраслях математики, механики и др. В дифференциальной геометрии детально исследовал свойство геодезических линий, впервые применил натуральные уравнения кривых, а главное, заложил основы теории поверхностей. Ввел понятие главных направлений в точке поверхности, доказал их ортогональность, вывел формулу для кривизны любого нормального сечения, начал изучать развертывающиеся поверхности и др. В одной посмертно опубликованной работе предварил исследования К.-Ф.Гаусса по внутренней геометрии поверхностей.

1.3. О классификации рабочих поверхностей деталей и инструментов

и соотношения С. Жермен1

tд и k2.д и k1.д и sin cos ,

(1.98)

где k1.д и и k2.д и – главные кривизны локального участка поверхности

Д И в заданной ее точке M

(причем k1.д и k2.д и );

Д И в точке M , составляющего угол с

kд и – кривизна плоского нормального сечения поверхности

первым главным сечением C1.д и ;

tд и – кручение поверхности

Д И в точке M в наперед заданном направлении на поверхности.

Формуле (97) эквивалентно соотношение (Koenderink, J.J., 1990, с. 228):

д и

cos2

2.д и

sin 2 H

д и

k1.д и k2.д и

cos 2 .

1.д и

Формула (97) позволяет определить кривизну текущего нормального сечения поверхности Д И , если

известны главные радиусы кривизны и угол между исследуемым сечением и одним из них.

Чтобы получить уравнение круговой диаграммы для кривизны и кручения локального участка поверхности Д И , перепишем уравнения (97) и (98) в виде

kд и 12 k1.д и k2.д и 12 k1.д и k2.д и cos 2 ;

tд и 12 k1.д и k2.д и sin 2

соответственно, после чего исключим из них параметр . Выполнив необходимые преобразования, приходим к уравнению окружности

k	k	k	k	2.д и	t	2	0 .	(1.99)
д и	1.д и	д и		2.д и		д и

В системе координат kд и tд и круговая диаграмма локального участка поверхности Д И представляет

2.д и

собой окружность радиуса

1.д и

с центром

1.д и

, 0

. Обратим внимание на то, что

k1.д и k2.д и

Д И в точке M . Задаваемая уравнением

Mд и – т.е. равно средней кривизне поверхности

(99) круговая диаграмма пересекает ось абсцисс (рис. 1.20) в точках

k1.д и , 0

и k2.д и , 0 .

Прежде, чем перейти к рассмотрению круговых диаграмм локальных участков поверхности Д И ,

дополнительно введем в рассмотрение их векторные диаграммы. Для этого требуется кратко рассмотреть доказательство следующей теоремы (Nutbourn A. A., Martin R., 1988):

1Жермен, Софи (Germain , Sophie) (1.4.1776 – 17.6.1831) – французский математик и механик, родилась в Париже, дочь ювелира. Самостоятельно изучила метаматику. Состояла в переписке с Ж.Л.Д'Аламбером, Ж.Л.Лагранжем, К.-Ф.Гауссом. Оказала Гауссу существенную поддержку в 1807, когда французские войска оккупировали Ганновер. Разрабатывала теорию чисел, теорию упругости и

теорию колебаний. Доказала невозможность положительного решения в целых числах выражения xn yn zn , если x, y, z – простые

числа, не равные друг другу, а n – любое простое число меньше 100. Вывела несколько формул, названных ее именем. В развитии

математической физики труды Жермен являются основополагающими. Нашла ряд важных положений в теории упругих пластинок.

Написала также “Рассуждения о состоянии наук и литературы в различные культурные эпохи” (1833). Премия Института Франции

(1816).

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 609 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете Технология машиностроения

#
23.02.202324.47 Mб11Radzevich, S.P. Monograph - 2001.pdf
#
23.02.20237.23 Mб4Горбацевич - Курсовое проектирование по ТМ.doc
#
23.02.2023949.47 Кб3Мешкова - Организация Технологии Отрасли.pdf
#
23.02.20234.4 Mб1Оптимизация Технологических Систем (укр).pdf
#
23.02.2023882.47 Кб3Основные Положения Теории Базирования (Лекции).pdf
#
23.02.20231.01 Mб6Основы Проектирования ТП.pdf