Добавил:

Mehanik Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Технический Университет им. Р.Е. Алексеева

Предмет:

Технология машиностроения

Файл:

Radzevich, S.P. Monograph - 2001

.pdf

Скачиваний:

Добавлен:

23.02.2023

Размер:

24.47 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 607 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

60	1. Рабочие поверхности деталей и инструментов

Вряде случаев преобразование аналитического представления геометрической информации о поверхности

ДИ из одного вида в другой может быть неоправданно трудоемким или технически невыполнимым. Это

указывает на необходимость рассмотрения возможности перехода (создания своеобразного “мостика”) от каждого из рассмотренных и др. способов аналитического описания поверхности Д И к обобщенному

аталитическому описанию их в натуральной форме. Такой переход возможен также при использовании специальных способов аналитического и дискретного представления исходной геометрической информации о поверхностях деталей и инструментов, используемых в практике отраслевого машиностроения.

1.2.2.7. Натуральная форма. Непрерывным (аналитическим) способам описания поверхностей деталей и инструментов свойственна большая определенность и однозначность, возможность получения полной и

достоверной информации о геометрической структуре и строении локального участка поверхности Д И в

дифференциальной окрестности текущей точки на ней, большая или меньшая простота вычисления частных производных по каждому из параметров и др. Вместе с тем рассмотренные выше аналитические методы аналитического описания поверхностей неудобны тем, что они всегда связаны с определенной системой отсчета.

Подобно тому, как пространственную кривую можно описать натуральным уравнением двумя внутренними параметрами: ее кривизной и кручением в функции длины дуги кривой (т.е. в функции положения

точки на кривой), так и поверхность Д И можно аналитически описать в функции положения точки на поверхности двумя внутренними параметрами – ее первой Ф1.д и и второй Ф2.д и основными квадратичными формами. Согласно теореме Бонне1, являющейся основной теоремой в теории поверхностей, гауссовы

коэффициенты Eд и , Fд и , Gд и первой	Ф1.д и и		Lд и , Mд и ,				Nд и второй				Ф2.д и основных квадратичных
форм, удовлетворяющие неравенствам E	д и	0,	G	д и	0, E		G	д и	F	2	0 и условиям совместимости,
	д и			д и		д и		д и		д и

определяемым уравнениями Гаусса (его theorema egregium) и Петерсена2-Кодацци3, однозначно определяют поверхность Д И с точностью до ее расположения и ориентации в пространстве.

Две поверхности с одинаковыми квадратичными формами Ф1.д и и Ф2.д и взаимно конгруэнтны или

симметричны одна другой (Фавар, Ж., 1960, с.251).

Определение двух основных квадратичных форм Ф1.д и и Ф2.д и поверхности Д И равносильно зада-

нию этой поверхности в натуральной форме.

Если одна гладкая поверхность может быть получена из другой путем изгибания первой, то в соответствие с теоремой Гаусса полные кривизны этих поверхностей в соответствующих точках совпадают. Другими

словами, гауссова кривизна	~	является инвариантом изгибания поверхности	Д И . Поэтому она может
	Gд и

1Бонне, Пьер Оссиан (Bonnet , Pierre Ossian ) (22.11.1819 – 22.6.1892). Французский математик, родился в Монпелье. Окончил Политехническую школу в Париже (1838). Работал на Парижском факультете наук (с 1878 – профессор), член Бюро долгот (с 1862). Основные исследования относятся к математическому анализу и дифференциальной геометрии. Усовершенствовал и распространил метод Коши решения дифференциальных уравнений с частными производными первого порядка при любом числе переменных. Вывел упрощенные формы логарифмических критериев. Определил кривые постоянной кривизны и ввел понятие геодезической кривизны. Изучил (1848) изотермическую сеть, линии в которой имеют постоянную геодезическую кривизну (сеть Бонне). Доказал (1865) теорему о существовании и единственности поверхности с заданными первой и второй квадратичными формами. Ряд работ посвящен механике упругого тела и аналитической механике.

2Петерсен, Карл Михайлович (25.05.1828 – 01.05.1881) – русский математик. Родился в Риге. Окончил Дерптский университет (1853). С 1865 преподавал в Петропавловском училище в Москве. Работы посвящены дифференциальной геометрии. Вывел основные свойства коэффициентов так называемой второй основной квадратичной формы поверхности и решил вопрос об аналитических условиях, определяющих саму геометрическую форму поверхности. Дополнил (1853) уравнения Гаусса о соотношениях между первой и второй основными квадратичными формами еще двумя уравнениями (уравнения Гаусса-Петерсена). Эти результаты не публиковались и были переоткрыты А.Майнарди (1857) и Д.Кодацци (1868). Поэтому в иностранной литературе эти уравнения носят название уравнений совместимости Майнарди-Кодацци. Изучал свойства кривых и поверхностей на главном основании, работал в области теории дифференциальных уравнений в частных производных. Основатель московской геометрической школы. Один из основателей Московского математического общества (1865).

3Кодацци, Дельфино (Codazzi, Delfino) (7.3.1824 – 21.7.1873) – итальянский математик, родился в Лоди. С 1865 – профессор Павийского университета. Основные работы посвящены теории кривых и теории поверхностей. Работа о развертывающихся поверхностях в 1861 была премирована Парижской АН. В дифференциальной геометрии известны уравнения Майнарди-Кодацци (Майнарди опубликовал их в 1857, а Кодацци (с полным выводом) в 1868-1869. Другие исследования относятся к теории геодезических треугольников, а также к устойчивости плавающих тел.

1.2. Задание рабочих поверхностей деталей и инструментов. Расчет элементов их локальной геометрии

быть выражена только через коэффициенты первой основной квадратичной формы Φ1.д и их производные по параметрам Uд и и Vд и . Аналитически это записывается так:

поверхности Д И и

Eд и

д и

Fд и

Gд и

Fд и

Uд и

Vд и

Eд и Gд и Fд и

Gд и

д и

Fд и

Gд и

Fд и

Gд и

Vд и

Uд и

Vд и

2 E

F 2

Uд и

д и

F 2

д и

F 2

д и

Условия совместимости Петерсена-Кодацци (Майнарди1-Кодацци) записываются так:

Lд и

Mд и

д и

;

Vд и

U д и

д и 12

Mд и

Nд и

д и

2 .

Vд и

U д и

д и 22

д и

В этих уравнениях через ikj обозначены символы Кристоффеля2 второго рода. Они выражаются через коэффициенты Eд и , Fд и и Gд и первой основной квадратичной формы Φ1.д и поверхности Д И (см. ниже,

раздел 1.2.5.2).

Проверка условий совместимости по уравнениям Гаусса и Майнарди-Кодацци обычно требуется в исключительных случаях – очевидность их выполнения следует из того, что заданные поверхности Д И изна-

чально являются гладкими регулярными.

1Майнарди, Анджело (1800 – 9.3.1879) – итальянский математик, профессор. Работал профессором в Павийском университете. В 1856 Майнарди решил задачу об определении поверхности по заданным основным квадратичным формам. Соответствующие уравнения вывел полностью в 1886-1869 Д.Кодацци. Поэтому теперь их называют уравнениями Майнарди-Кодацци, хотя еще раньше (1853) их вывел русский математик К.М.Петерсен в диссертации “Об изгибании поверхностей”, которая тогда не была опубликована.

2Кристоффель, Эльвин Бруно (Christoffel , Elwin Bruno) (10.11.1829, Моншау, – 15.3.1900, Страсбург ) – немецкий математик, родился в Моншау. Окончил Берлинский университет (1856). Работал там же (с 1859), в Цюрихском политехникуме (с 1869 – профессор), в Берлинской ремесленной академии (с 1869), в Страсбургском университете (с 1872 – профессор). Основные исследования относятся к римановой геометрии, теории инвариантов, теории поверхностей и конформному отображению. Известен работами в области теории функций, теории дифференциальных уравнений с частными производными, теории инвариантов алгебраических форм и теории дифференциальных квадратичных форм, где Кристоффелем введен (1869) символ, носящий его имя. В области теории поверхностей известна теорема Гаусса-Кристоффеля. В теории инвариантов дал необходимые и достаточные условия эквивалентности двух алгебраических форм n переменных порядка p . Ввел символы Кристоффеля первого и второго порядков, и символы Римана-Кристоффеля.

Занимался теорией дифференциальных уравнений с частными производными, в частности применением в этой теории методов конформного отображения (теорема Шварца-Кристоффеля). Вместе с Э.Бельтрами и Р.Липшицем явился непосредственным продолжателем идей Г.Ф.Б.Римана. Работал в области ударных волн. Разрабатывал (1869) идеи, положенные в основу тензорного анализа.

62 1. Рабочие поверхности деталей и инструментов

Исследование любой поверхности Д И будет приведено к каноническому виду, если определены ее первые две основные квадратичные формы Φ1.д и и Φ2.д и .

Гауссовы коэффициенты первых двух основных квадратичных форм Ф1.д и и Ф2.д и могут быть

определены при различных способах задания исходной геометрической информации о поверхности Д И как в

непрерывной, так и в дискретной форме. Задание поверхностей деталей и инструментов в естественной форме, а именно через первые две основные квадратичный формы Ф1.д и и Ф2.д и , обеспечивает возможность

аналитического решения задач формообразования сложных поверхностей деталей на многокоординатных станках с ЧПУ, позволяет получать необходимые зависимости и рассчитать параметры поверхности Д И в

простой и удобной форме без обязательной их привязки к системе координат, в которой они заданы изначально. Существенным преимуществом аналитического описания поверхности Д И в натуральном виде является то,

что такой способ позволяет в простой форме определять все необходимые элементы локальной геометрии гладких регулярных участков поверхности Д И и принципиально просто реализуется как на ЭВМ, так и в

системах ЧПУ многокоординатными металлорежущими станками. Однако при этом возникает дополнительная задача приведения исходных способов задания поверхности Д И к естественному.

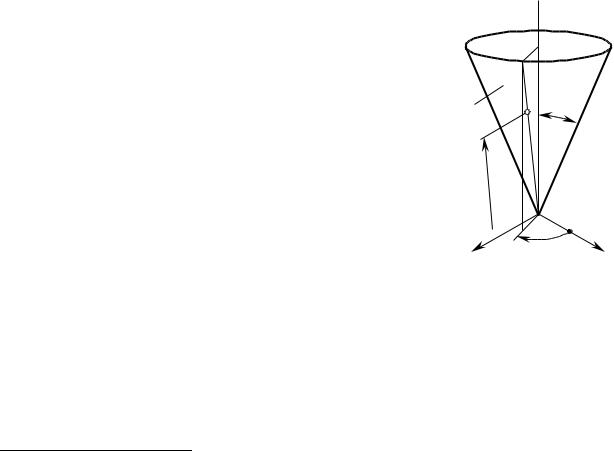
Пример 1.2. Рассмотрим порядок определения первых двух основных квадратичных форм Φ1.д и				и Φ2.д и
Д И (рис. 1.11), заданной уравнением
		rд и (Uд и , Vд и ) iUд и sin cos jUд и sin sin kUд и cos .
Предполагая, что Uд и sin 0 , единичная нормаль к поверхности конуса будет
	rд и	rд и
n д и	U д и	Vд и	i cos cos j cos sin k sin .
	U д и	Vд и
	rд и	rд и
	rд и	rд и
	U д и	Vд и
	U д и	Vд и

Первая и вторая основные квадратичные формы поверхности будут соответственно равны:

Ф1.д и dU д2 и U д2 и sin 2 d 2 ;

Ф2.д и U д и sin cos d 2 .

Пример 1.3.1 Требуется рассчитать коэффициенты Eд , Fд , Gд первой Φ1.д и Lд , Mд , Nд второй Φ2.д основных квадратичных форм эвольвентной винтовой поверхности Д зуба косозубого колеса.

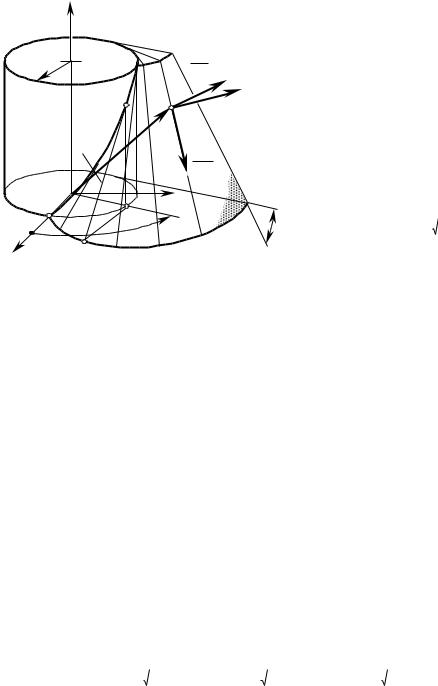
Уравнение поверхности Д (рис. 1.12) записываем в виде матрицы:

Д И

Uд и

Yд и

для конической поверхности

Zд и

Xд и

rb.д cosVд Uд cos b.д sinVд

sinV U

sin

b.д

sinV

b.д

tan

sin

b.д

Здесь U д и Vд – гауссовы координаты текущей точки на поверхности Исходя из этого уравнения, запишем:

Рис. 1.11. К примеру расчета основных квадратичных форм Ф1.д и и Ф2.д и

конического участка поверхности

Д И .

Д (см. рис. 1.12).

1Пример разработан совместно с канд. техн. наук, доцентом В.А.Палагутой.

1.2. Задание рабочих поверхностей деталей и инструментов.
Расчет элементов их локальной геометрии	63
	63

	Zд
rb.д				rд
				Vд
			A	Nд
				Nд
				М
		Uд		rд
		Uд		rд
				rд
				Uд
D				b.д
D				Yд
				B
Xд	Vд
	Vд	C
		C

Рис. 1.12. К примеру определения коэффициентов первой и

второй квадратичных форм.

cos b.д sinVд

rb.д sinVд Uд cos b.д cosVд

cos

b.д

cosV

cosV U

cos

b.д

sinV

;

b.д

sin

b.д

tan

b.д

2 cos4

b.д

r 2

Поэтому

Eд

1 ,

Fд

b.д

и Gд

b.д

cos b.д

cos2 b.д

На основании этих результатов получим:

2 cos4

b.д

r 2

ds2

b.д

2 .

1.д

cos b.д

cos2 b.д

Дискриминант Hд

первой основной

квадратичной

формы

поверхности

Д равен Hд

EдGд Fд2 Uд cos b.д .

Касательная плоскость к поверхности

проходит через два

направления, касательные к Uд

и Vд линиям на ней.

Направ-

ление, касательное к Uд линии на

Д определяется уравнением:

rд

cos

b.д

sinV j

cos

b.д

cosV k

sin

b.д

Uд

Второе направление касательно к Vд координатной линии на

Д и соответственно равно:

rд

sinV U

cos

b.д

cosV j

cosV U

cos

b.д

sinV k

tan

b.д

Vд

b.д

д b.д

Приведенные результаты позволяют записать уравнение касательной плоскости

КП ,

проходящей через точку M XM ,YM , ZM на

поверхности Д :

XКП XM

YКП YM

ZКП ZM

rКП

cos b.д sinVд

cos b.д cosVд

sin b.д

sinVд U д cos b.д cosVд

cosVд Uд cos b.д sinVд

rb.д tan b.д

где XКП , YКП и ZКП – координаты текущей точки касательной плоскости КП .

Нормаль к поверхности

Д детали определяется так:

Nд iдNд.X jдNд.Y k дNд.Z .

Орт нормали равен:

n д iд

Nд.X

jд

Nд.Y

k д

Nд.Z

Nд2.X Nд2.Y Nд2.Z

Здесь:

Yд

Zд

cos b.д cosVд

sin b.д

д.X

Uд

sin

b.д

cos

b.д

sinV

;

cosV U

cos

sinV

tan

b.д

Vд

1. Рабочие поверхности деталей и инструментов

Zд

Xд

Zд

cos b.д sinVд

sin b.д

Uд

sin

b.д

cos

b.д

cosV

;

д.Y

sinV U

cos

cosV

tan

b.д

Vд

Xд

Yд

cos b.д sinVд

cos b.д cosVд

Uд

cos2

b.д

д.Z

sinV

cos

cosV

cosV U

cos

sinV

b.д

Поэтому:

Vд

i U

sin

b.д

cos

b.д

sinV j U

sin

b.д

cos

b.д

cosV k

cos2

b.д

д д

sin

b.д

cos

b.д

sinV

sin

b.д

cos

b.д

cosV

cos

b.д

Nд

В этом уравнении

2 sin

b.д

cos2

b.д

sin 2 V U 2 sin

b.д

cos

b.д

cos2 V U

2 cos4

b.д

cos

b.д

поэтому можно записать:

n д iд sin b.д sinVд jд sin b.д cosVд k д cos b.д

Вторая основная квадратичная форма поверхности

Д находится так:

cos b.д cosVд

rb.д cosVд Uд cos b.д sinVд

d 2r

0 0

0 1 T ;

cos

sinV

sinV U

cos

cosV

b.д

д ;

b.д

;

Поэтому Lд 0;

Mд 0;

Nд

Uд sin b.д cos b.д . На основании этих результатов получим:

sin

b.д

cos

dV2 .

2.д

b.д

Дискриминант T

второй основной квадратичной формы Φ

равен

L M

0 .

2.д

1.2.3. Разложение уравнения поверхности Д(И) в ряды. В случаях, когда аналитическая форма (7)

задания уравнения поверхности Д И приводит к громоздким преобразованиям и техническим трудностям

при вычислениях, следует проанализировать целесообразность разложения функции (7) в ряды. Уравнениями (3) векторная функция rд и rд и Uд и , Vд и определяется через скалярные функции

Xд и , Yд и , Zд и . Если все скалярные функции (3) дифференцируемы вплоть до порядка n 1 и существу-

ет n я	производная, т.е. в окрестности значений параметров	U	M	и	V M	все три скалярные функции
			д и		д и

раскладываются в ряд Тэйлора, вектор-функцию (7) также можно разложить в ряд Тэйлора в окрестности этих

же значений U	M	и V	M параметров:
	д и	д и
			rд и Uд и h;	Vд и k

1.2. Задание рабочих поверхностей деталей и инструментов.

Расчет элементов их локальной геометрии

д и

rд и

д и

n 1

д и

1 !

д и

	rд и			rд и		n
1	rд и			rд и
			h			k . 0	1.
			h			k . 0	1.

n!	Uд и UM h			Vд и UM h
		VM k			VM k

Разложение функции (7) в ряд Тейлора может существенно упростить расчет геометрических характеристик локальных участков поверхности Д И .

Наряду с использованием разложения вектор-функции вида (7) в ряд Тейлора, находит применение разложение в ряд Маклорена и в другие ряды (Бронштейн И.Н, Семендяев К.А., 1986).

При использовании функций, разложенных в ряд, следует помнить, что их почленное интегрирование возможно только при равномерной сходимости ряда.

1.2.4. Требования к аналитическому представлению геометрической информации о поверхности

Д(И). При организации управления многокоординатной обработкой деталей с помощью ЧПУ математические модели поверхностей деталей и инструментов должны обеспечивать возможность формирования траекторий движения инструмента относительно детали и контроля точности обработки. Следствием этого является ряд

требований к аналитическому представлению геометрической информации о поверхности Д И как слож-

ной, так и относительно простой формы.

Пусть исходная поверхность Д И с собственными параметрами U д и и Vд и в своей системе координат Xд и Yд и Zд и задана матрицей-столбцом:

д и

, V

д и

rд и

, V

д и

(1.60)

, V

д и

В это уравнение входят действительные функции

Xд и Uд и , Vд и ,

Yд и Uд и , Vд и

Zд и Uд и , Vд и

действительных

переменных

Uд и

и Vд и ;

сама

же функция

rд и rд и U д и , Vд и будет векторной

функцией скалярного аргумента.

Функция

rд и rд и U д и , Vд и должна быть гладкой. Принадлежность функции классу гладкости

C n означает,

что она имеет непрерывные частные производные до порядка

n включительно. Для вектор-

функции (60) запись

д и

, V

д и

, V

;

, V

д и

д и д и

д и

д и д и

д и

д и д и

д и

означает, что каждая из координат

Xд и , Yд и

и Zд и

как функция параметров Uд и

и Vд и принадлежит

C n . Запись r

д и

, V

требует только непрерывности по совокупности аргументов. Требование

д и

непрерывности поверхности Д сводится к тому, чтобы форма (60) ее представления была непрерывной функцией аргументов Uд и и Vд и .

66	1. Рабочие поверхности деталей и инструментов

Полагаем, что все производные, которые необходимы для решения задачи синтеза наивыгоднейшего формообразования поверхности детали (а это, как правило, производные не выше второго порядка), существуют и непрерывны, подразумевая при этом, что операции, которые описываются ниже, следует прекратить, когда входящие в рассмотрение производные перестают удовлетворять этому требованию.

Если отсек поверхности Д И в пределах ограничивающего его контура обладает тем свойством, что

каждый его локальный участок является простым1 и в этой же области поверхность имеет непрерывные все частные производные первого порядка – следовательно допускается повторное дифференцирование и

уравнение поверхности Д И имеет вторые производные, то такой отсек будет регулярным.

Необходимым и достаточным условием того, чтобы отсек поверхности Д И был гладким регулярным,

является требование неравенства нулю в пределах ограничивающего его контура по крайней мере одного из якобианов (13)-(15).

Иными словами для гладкого регулярного отсека поверхности Д И выполняется условие:

(1.61)	J x2 J y2 J z2 0 .
Соотношение (61)	является условием невырождения поверхности Д И в точку или в линию. Его

выполнение необходимо для того, чтобы локальные участки поверхности не были сингулярными (не находились в окрестности особых точек на поверхности Д И ). Вместе с тем выполнение условия (61) не

всегда достаточно для исключения сингулярностей на поверхностях – это следствие того, что оно отражает не только особенности геометрической структуры поверхности Д И в текущей точке на ней, но зависит также

и от характера параметризации этой поверхности. Например, если координатную плоскость XY , задать уравнениями X U , Y V , Z 0 , то J z 1 0 . Но если ту же плоскость параметризовать иначе: X U 3 ; Y V3 ; Z 0 , то в начале координат получим J x J y J z 0 и условие (61) не выполняется.

Выполнение условия (61) можно проверять в иной форме: требуется, чтобы через каждую точку на поверхности Д И проходили две и только две координатные линии Uд и Const и Vд и Const , име-

ющие в этой точке две несовпадающие одна с другой касательные. Иными словами, параметры Uд и и Vд и

должны быть независимыми.

Требование независимости U д и , Vд и параметров означает, что ранг матрицы

	Xд и			Yд и

		Uд и		Uд и
M		Uд и		Uд и
		X	д и	Y
			д и	д и
		V		V
		д и		д и

Zд и

Uд и

Zд и

Vд и

должен быть равен двум. Точки, где ранг матрицы M равен 1 и 0, являются сингулярными. Если ранг мат-

рицы M во всех точках равен 1 – поверхность вырождается в кривую. Это имеет место, например, в

случае: X U V ; Y (U V)2 и Z (U V)3 .

Если два определителя матрицы M вырождаются в нуль, в нуль вырождается и третий, т.е. все три вырождаются одновременно (кроме столбца, состоящего из двух нулей), но вырождение в нуль только одного

определителя не свидетельствует о том, что локальный участок поверхности	Д И в окрестности такой точки
сингулярный. Если, например, некоторая поверхность задана уравнениями	X U V ; Y U V и Z UV,

1Помним, что отсек поверхности Д И будет простым, если координаты текущей точки на нем могут удовлетворять уравнению вида

Zд и Zд и Xд и , Yд и .

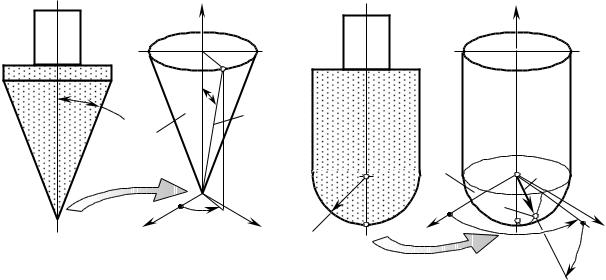
1.2. Задание рабочих поверхностей деталей и инструментов.

					Расчет элементов их локальной геометрии					67

тогда X	Y	X	Y	0 , но	X	Z	X	Z	0 и поверхность представляет собой плоскость,

U	V	V	U		U	V	V	U
проходящую через ось Z .
Другой пример: X X U ; Y Y U						и Z V, когда поверхность является цилиндром.

Еще одна возможность проверки уравнения поверхности Д	И на наличие сингулярных точек на ней:
если уравнение поверхности Д И записано в векторной форме	rд и rд и U д и , Vд и , условие, по кото-

рому ранг матрицы M равен двум, может быть записано в форме:

rд и

или так

det

0 .

д и

Появляющиеся вследствие особенностей строения поверхности и вследствие выбранной ее параметризации сингулярные точки (собственно сингулярные и ложные точки) часто встречаются при решении задач многокоординатного формообразования сложных поверхностей деталей на станках с ЧПУ, например, при конструировании режущих инструментов и аналитическом описании их исходной инструментальной поверхности И .

	Zu		Zu
		M
u	u
u		Uu
		Uu
И
			И	rи
Yu		Xu ru	М	Xu
Yu	V	Xu ru	Yu
	u
			Vu	Uu
1.			2.

Рис. 1.13. Примеры сингулярностей на исходной инструментальной поверхности И .

Примером собственно сингулярной точки служит вершинная точка кругового конуса на исходной инструментальной поверхности И конического инструмента (рис. 1.13.1). В этом случае координаты точек поверхности И удовлетворяют уравнению:

rи iиUи sin и sin Vи jиUи sin и cosVи k иUи cos и,

где и – угол при вершине исходной инструментальной поверхности И инструмента. Для рассматриваемого случая

	sin		sinV	sin		cosV	cos
M		и	и		и	и	0	и	.
Uи sin		и cosVи		Uи sin и sinVи			0

68	1. Рабочие поверхности деталей и инструментов

Следовательно, при Uи 0 (т.е. в вершине поверхности И ) имеется сингулярная точка – это изоли-

рованная точка поверхности, в которой строение поверхности И отличается от строения этой же поверхности в других ее точках.

Примером ложной сингулярности, вызванной особенностями параметризации поверхности, а не ее строением, служит полярная точка сферы на исходной инструментальной поверхности И цилиндрического инструмента со сферическим концом (рис. 1.13.2). Сферический участок поверхности И может быть параметризован уравнением

rи iиrи cosUи sin Vи jиrи cosUи cosVи k иrи sin Uи ,

где rи – радиус сферического участка исходной инструментальной поверхности И . Исходя из уравнения сферического участка поверхности И имеем:

rи sinUи sinVи			rи sinUи cosVи				rи cosUи
[M] r cosU	и	cosV	r cosU	и	sinV	0	.
и	и	и	и	и	и
В рассматриваемом случае поверхность		И имеет сингулярную точку при Uи						: это ложная сингу-
								2
лярная точка – следствие исключительно выбора вида параметризации поверхности И .
Рассмотренные примеры свидетельствуют о			необходимости			выполнения проверки уравнения

поверхности Д И (или ее отсеков) на наличие сингулярных точек.

Приведенные сведения позволяют дополнить требования к аналитическому описанию и виду параметризации поверхности Д И , а именно: чтобы поверхность Д И была гладкой, не имела выступов или складок,

все три частные производные должны быть непрерывны – сингулярные точки могут быть там, где Д 0 (и

И 0 ).

Проверку выполненния требований, предъявляемых к аналитическому представлению геометрической информации о поверхности Д И , удобнее выполнять, если ее уравнение представлено в локальной системе

координат. Локальная система координат внутренне связана с поверхностью Д И , вследствие чего называют внутренней. Если локальная система координат естественным образом связана с поверхностью Д И , а

это имеет место, когда в качестве координатных линий на поверхности приняты линии ее кривизны, получим канонический репер1, называемый также трехгранником Дарбу2. Его использование часто позволяет избежать громоздких преобразований.

Требования к аналитическому описанию поверхности Д И , приведенные выше, являются основными и

должны удовлетворяться всегда. По мере необходимости они дополняются другими требованиями, существенными при решении конкретных задач.

1.2.5. Дискретное задание и элементы локальной геометрии сложных поверхностей деталей и инструментов. Получение геометрической информации о строении сложной поверхности Д детали часто

основывается на результатах исследований технических характеристик этих поверхностей (аэро-, гидро-, газодинамических и др.) – это следствие сложности строения и геометрической структуры рабочих

1Метод подвижного трехгранника разработан Френе (J.Frenet) для исследования пространственных кривых. Применительно к исследованию поверхностей этот метод адаптирован (1880) Дарбу (G.Darboux): в каждой точке поверхности существует два направления экстремальной нормальной кривизны, известных как главные направления; совместно с единичной нормалью они определяют единственный главный трехгранник, чрезвычайно удобный в применении. В общей постановке метод подвижного репера развит Картаном (E.Cartan ) – он в полном объеме показал потенциальные возможности и преимущества метода подвижного репера.

2Дарбу, Жан Гастон (Darboux , Jean Gaston) (13.8.1842, Ним, - 23.2.1917, Париж), французский математик. Член Парижской АН (1884), с 1900 непременный секретарь ее; чл.-корр. Петербургской АН (1895). Основные труды посвящены проблемам дифференциальной геометрии (теория поверхностей, теория криволинейных координат) – “Лекции по общей теории поверхностей” (тт. 1-4, 1887-96) и

“Лекции об ортогональных системах и криволинейных координатах” (1898). Геометрические исследования привели Дарбу к рассмотрению различных вопросов интегрирования дифференциальных уравнений. Из работ, относящихся к другим областям математики, важны мемуары по теории интегрирования, теории аналитических функций, а также исследования по вопросу о разложении функций по ортогональным функциям, в частности полиномам Якоби. В механике плодотворно занимался различными вопросами кинематики, равновесия, малых колебаний системы точек и др.

1.2. Задание рабочих поверхностей деталей и инструментов.
Расчет элементов их локальной геометрии	69
	69

поверхностей многих деталей и экспериментальным либо численным подходом к получению координат их точек, например, в виде числовых отметок. Поэтому на практике информация о сложной поверхности Д

часто задается таблично числовыми отметками, координатами отдельных точек на поверхности детали с указанием направления нормалей или касательных к Д в них, системой двух трансверсальных семейств

определенным образом расположенных на поверхности Д линий, графически в виде чертежа на плазе и др. Задача получения необходимой полной геометрической информации о дискретно заданной поверхности Д

является неотъемлемой составной частью проблемы синтеза наивыгоднейшего формообразования сложной поверхности детали на многокоординатном станке с ЧПУ.

Геометрическая информация о дискретно заданной поверхности Д принципиально может быть полу-

чена непосредственно из данных об элементах, задающих поверхность, например по координатам точек, принадлежащих Д . Для этого можно использовать методы аналитической обработки дискретно заданных

функций двух переменных. Такой подход связан с необходимостью выполнения в большом объеме вычислений. Очевидно, что вследствие неполного задания поверхности Д он менее точен.

Для увеличения точности расчетов требуется большая плотность элементов, задающих поверхность, особенно на ее участках с большой кривизной. Это приводит к еще большему объему вычислений. Поэтому на практике дискретно заданную рабочую поверхность детали целиком либо по частям заменяют аналитически описанными поверхностями заданного вида. Во втором случае – отсеками таких поверхностей с решением вопросов их стыковки по условию непрерывности или исходя из требования достижения требуемого порядка гладкости.

В качестве аппроксимирующих поверхностей часто используются поверхности второго и более высоких порядков, реже поверхности других типов. Для получения аппроксимационных формул с производными широкое распространение получила сплайн-аппроксимация поверхности Д сплайн-функциями степени k .

Сплайн-аппроксимация позволяет получать простые уравнения отсеков поверхностей Д достаточно больших

площадей. В приложениях часто бывает достаточно применить только кубическую или бикубическую сплайнаппроксимацию, что существенно упрощает решение задач многокоординатного формообразования сложных поверхностей деталей.

Здесь и далее термин отсек поверхности Д детали предполагает:

Определение 1.4. Отсек поверхности Д – это сопряженный с другими из условия непрерывности или

по требуемому порядку гладкости участок одной (сплошной) обрабатываемой поверхности детали, ограниченный криволинейным многоугольником, внутри которого поверхность описывается одним уравнением.

Из отсеков поверхности состоит ее фрагмент. В частных случаях отсек и фрагмент поверхности могут совпадать один с другим.

Обычно границы отсека поверхности Д представляют собой криволинейные многоугольники

(рис. 1.14). Вместе с тем нет принципиальных ограничений на то, чтобы они имели форму замкнутого полностью или частично криволинейного контура.

Кратко рассмотренные выше способы дискретного задания и аналитического описания поверхностей деталей далеко не исчерпывают всего многообразия способов, встречающихся в практике, особенно в практике отраслевого машиностроения.

Для эффективного применения дифференциально-геометрического метода формообразования поверхностей при механической обработке деталей требуется создание своеобразного “мостика” – перехода от

исходного задания геометрической информации о поверхности Д И к аналитическому их описанию в нату-

ральной форме. При этом следует помнить, что вид задания и аналитического описания (параметризации) поверхности Д И оказывает существенное влияние на эффективность решения задачи синтеза, в частности

уже потому, что трудоемкость определения и точность расчета первых и вторых производных от rд и по

Uд и Vд –параметрам при различных способах задания поверхности Д И различна.

1.2.5.1.Сложные поверхности деталей и инструментов, аппроксимированные сплайнами. Заданные исходно в дискретной форме (координатами лежащих на них точек) сложные поверхности деталей могут быть предварительно аппроксимированы аналитическими функциями, после чего элементы их локальной гео-

<<< < Предыдущая 1 2 3 4 5 67 / 607 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете Технология машиностроения

#
23.02.202324.47 Mб11Radzevich, S.P. Monograph - 2001.pdf
#
23.02.20237.23 Mб4Горбацевич - Курсовое проектирование по ТМ.doc
#
23.02.2023949.47 Кб3Мешкова - Организация Технологии Отрасли.pdf
#
23.02.20234.4 Mб1Оптимизация Технологических Систем (укр).pdf
#
23.02.2023882.47 Кб3Основные Положения Теории Базирования (Лекции).pdf
#
23.02.20231.01 Mб6Основы Проектирования ТП.pdf