Добавил:

Mehanik Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Технический Университет им. Р.Е. Алексеева

Предмет:

Технология машиностроения

Файл:

Radzevich, S.P. Monograph - 2001

.pdf

Скачиваний:

Добавлен:

23.02.2023

Размер:

24.47 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 6010 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

1. Рабочие поверхности деталей и инструментов

Теорема 1.1. Если для некоторого локального

tд и

участка гладкой регулярной поверхности

Д И в

текущей ее точке M известны главные кривизны

k1.д и и

k2.д и , измеренные в заданных единичны-

k2.д и

k1.д и

kд и

ми векторами

t1.д и

и t 2.д и

главных

секущих

плоскостях C1.д и и C2.д и , то текущие значения

нормальной кривизны

kд и и кручения

tд и

kд и ( ),tд и ( )

этой поверхности в направлении t д и ,

состав-

ляющем угол

с первым главным сечением C1.д и ,

Рис. 1.20. Пример круговой диаграммы выпуклого

будут соответственно равны:

cos2 k

sin 2

локального участка гладкой регулярной

2.д и

;

поверхности

Д(И) .

д и

1.д и

tд и k2.д и k1.д и sin cos .

Отдельные фрагменты доказательства этой теоремы используются при построении векторных диаграмм локальных участков поверхностей Д И .

Исходим из того, что вектор единичной касательной к поверхности Д И в точке M в направлении, заданном углом , задается так:

(1.100)

t д и t1.д и cos

t 2.д и sin .

Вектор

другой единичной

касательной

поверхности Д И в точке M на ней,

д и

перпендикулярный t д и , в этом случае будет иметь вид

(1.101)

t *

2.д и

cos t

1.д и

sin .

д и

На основании (100) перемещение t д и dSд и можно разложить на две составляющие

t д и dSд и t1.д и cos dSд и t 2.д и sin dSд и .

Поскольку это перемещение производится в главных направлениях t1.д и и t 2.д и на поверхности Д И , то нормальные составляющие этих перемещений соответственно равны:

dN1.д и k1.д и t1.д и cos dSд и ; dN2.д и k2.д и t 2.д и sin dSд и .

Объединяя эти выражения, приходим к результату

(1.102) dNд и dN1.д и dN2.д и Nд и dSд и k1.д и t1.д и cos dSд и kд и t 2.д и sin dSд и .

Из уравнений (100) и (101) имеем

1.3. О классификации рабочих поверхностей деталей и инструментов

1.д и

cos t

sin ;

д и

sin t

cos .

(1.103)

2.д и

д и

Подставляя эти значения в (1.102), получим

д и

cos2 k

2.д и

sin 2

2.д и

sin cos dS

д и

(1.104)

1.д и

д и

1.д и

д и

Известно, что перемещение на dSд и в направлении t д и ведет к перемещению в нормальном направле-

нии

д и

(1.105)

д и д и

д и

Сопоставление формул (104) и (105) показывает, что теорема 1.1. доказана.

Для выяснения основных свойств круговых диаграмм локальных участков гладких регулярных

поверхностей

Д И

приведенное доказательство теоремы 1.1 позволяет ввести в рассмотрение их векторные

диаграммы относительно факторов

t д и

и Nд и . Для этого уравнение (100) и частично преобразованные

уравнения (102) и (105) перепишем совместно:

t д и t1.д и cos t 2.д и sin ;

Nд и k1.д и t1.д и cos k2.д и t 2.д и sin ;

Nд и kд и t д и tд и t *д и .

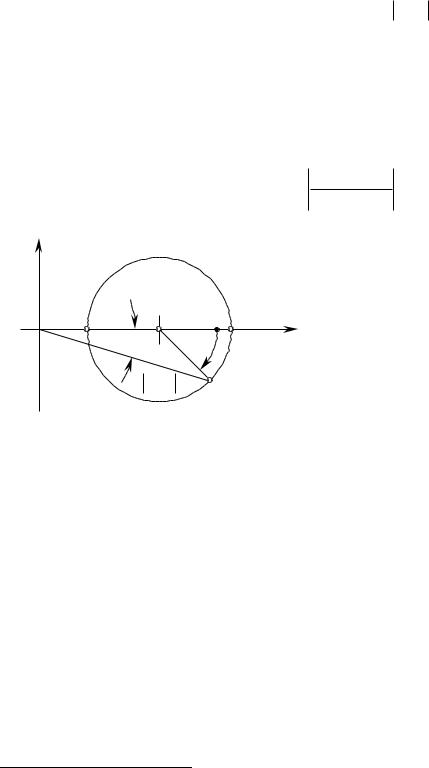
Пример векторной диаграммы поверхности

Д И сложной формы представлен на рис. 1.21.

Помним,

что

drд и t д и dSд и и

dNд и Nд и dSд и ,

поэтому

векторная диаграмма

является

изображением,

масштабированным

по

параметру

t 2.д и

t д и

dSд и (поскольку требуется, чтобы векторная диаграм-

ма была отнесена к параметрам drд и и dNд и ).

t д и

Векторы Nд и

t д и (или их противоположные

направления) однонаправленны для 0

или 90 ,

kд и cos

но они имеют различные направления при других

значениях угла ,

если k1.д и k2.д и .

sin

t1.д и

Из

рис. 1.21

следует, что

кручение

поверхности

д и

Д И

отрицательно

при

0 90

когда

kд и

Nд и

k1.д и k2.д и ;

следовательно

длина, показанная как

t д и

t д и (см. рис. 1.21), является положительной.

По теореме Пифагора из рис. 1.21 имеем

Рис. 1.21. Пример векторной диаграммы локаль-

cos2 k2

sin 2

t 2

ного участка гладкой регулярной по-

д и

1.д и

2.д и

д и

верхности Д(И) относительно пара-

метров t д и и Nд и .

1. Рабочие поверхности деталей и инструментов

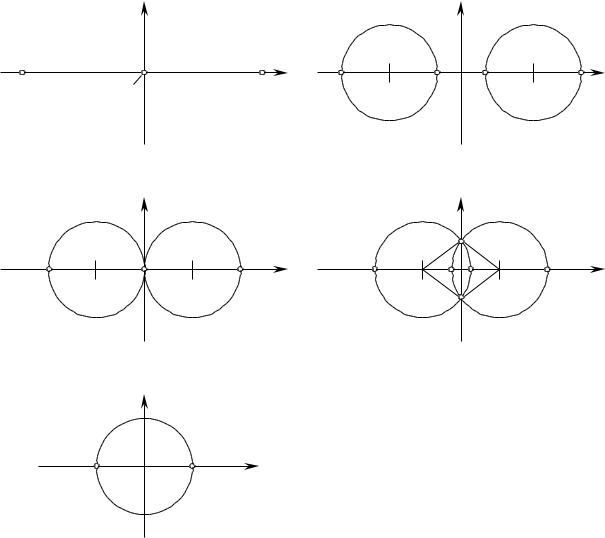
Обозначим через угол между векторами Nд и и t д и (см. рис. 1.21). На круговой диаграмме локаль-

ного участка поверхности

Д И (рис. 1.22) показана длина отрезка

N д и

и угол, равный по величине 1.

Для

случая, когда

k1.д и

положительно

k1.д и 0 ,

поведение

конца

вектора

Nд и нормали к

локальному участку поверхности

Д И будет следующим.

Если k2.д и также положительно

k2.д и 0

, круговая диаграмма не пересекает ось ординат tд и . Такой

локальный участок поверхности

Д И

будет

эллиптическим.

Возможное направление

вектора

Nд и

относительно направления t д и зависит от величины угла max , который определяется направлением OP в

положении, касательном к круговой диаграмме, и рассчитывается по формуле

max

sin 1

k1.д и k2.д и .

k1.д и k2.д и

В этом случае обе главные кривизны положи-

tд и

тельны, а поверхность

Д И локально выпукла.

Если k2.д и отрицательно

k2.д и 0 ,

круго-

вая диаграмма пересекает ось ординат tд и . Такой

k2.д и

k1.д и

локальный участок поверхности

Д И будет ги-

kд и

перболическим. Направление вектора Nд и может

быть любым; главные кривизны имеют противо-

Nд и

положные знаки, а поверхность

Д И локально

P k

( ),t

( )

выпукловогнутая.

д и

Если k2.д и равно нулю

k2.д и 0 , круговая

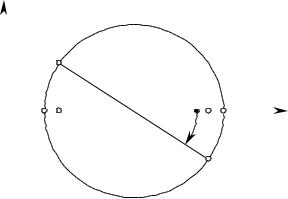
Рис. 1.22. Круговая диаграмма локального участка

диаграмма только касается

оси

ординат tд и , а

такого типа локальный участок поверхности

Д И

поверхности Д(И) (показаны угол и

абсолютная величина вектора Nд и ).

будет параболическим. Возможные направления

вектора Nд и ограничены пределами 90

отно-

сительно t д и . Если одна из главных кривизн равна нулю,

поверхность

Д И

локально можно рассматри-

вать как цилиндр.

Таким образом как только для заданной точки локального участка гладкой регулярной поверхности

Д И определены главные кривизны, нормальные

кривизны и кручение поверхности

Д И становятся

известными для всех направлений. Круговая диаграмма (см. рис. 1.22) наглядно показывает эту зависимость.

Теоретически поведение

нормали Nд и

поверхности

Д И

может быть определено из круговой

диаграммы, но поскольку dN д и N д и dSд и , вектор смещения конца единичной нормали к поверхности

Д И проще получить из векторной диаграммы (см. рис. 1.21).

Д И . Многие особенности

1.3.2.1. Использование круговых диаграмм локальных участков поверхности

локальной топологии гладкой регулярной поверхности

Д И могут быть просто

выведены исходя из

рассмотрения круговых диаграмм. При этом полагаем, что алгебраически наибольшая кривизна есть k1.д и ,

поэтому на круговой диаграмме она всегда будет обозначена правее кривизны k2.д и вдоль оси абсцисс. (за

1 Не следует пытаться показывать на круговой диаграмме (см. рис. 1.22) аргумент

вектора

Nд и , поскольку это не векторная

диаграмма.

Для построения угла следует

воспользоваться векторной

диаграммой локального

участка поверхности Д И (см.

рис. 1.21).

1.3. О классификации рабочих поверхностей деталей и инструментов

исключением случаев, когда локальный участок поверхности вырождается в омбилический локальный участок или в локальный участок уплощения).

1.3.2.2. Омбилические локальные участки поверхности Д И .

Если k1.д и

k2.д и , круговая диаграмма

стягивается в точку. Поэтому все

нормальные кривизны kд и

становятся

равны

друг

другу:

kд и

k1.д и k2.д и . Более того, в этом случае кручение поверхности

Д И во всех направлениях равно нулю

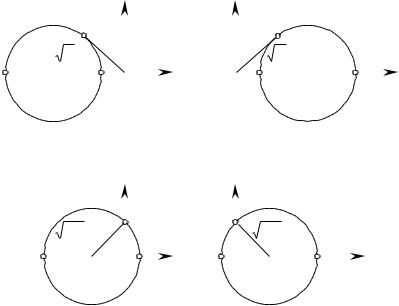
(рис. 1.23.1).

Вогнутый

Выпуклый

Вогнутый

Выпуклый

омбилический

tд и

омбилический

эллиптический tд и

эллиптический

k1.д и k2.д и kд и 0

k2.д и

k1.д и

k2.д и

k1.д и

k1.д и k2.д и 0

kд и

Уплощения

Вогнутый

Выпуклый

Гиперболический

параболический

tд и

параболический

(псевдовогнутый)

tд и

(псевдовыпуклый)

k2.д и

k1.д и

k2.д и

k1.д и

k2.д и

k1.д и

kд и

k2.д и

k1.д и

kд и

Гиперболический

(минимальный)

tд и

k2.д и

k1.д и

kд и

Рис. 1.23. Возможные виды круговых диаграмм

локальных участков гладких регулярных

поверхностей Д(И) .

1.3.2.3. Кручение поверхности

Д И .

Когда главные кривизны

k1.д и

k2.д и определены, текущие

значения нормальной кривизны kд и

и кручения

tд и

локального

участка поверхности

Д И

становятся определенными однозначно – их значения взаимоувязаны. В частности, это значит, что кручение поверхности детали или инструмента не является параметром, которым конструктор может варьировать,

синтезируя поверхность Д И .

Кручение поверхности максимально в направлении, составляющем угол 45 с главными направлениями


94				1. Рабочие поверхности деталей и инструментов
94
C1.д и и		C2.д и		локального участка поверхности Д И , где	его значения	достигают	величины
	k1.д и k2.д и		. Если в некотором заданном направлении кручение		поверхности	Д И равно	tд и , то
			. Если в некотором заданном направлении кручение		поверхности	Д И равно	tд и , то
2

кручение этой же поверхности в противоположном направлении (т.е. в направлении, составляющем угол 180 с заданным направлением) также равно tд и . Кручение поверхности Д И в направлении, ортогональном заданному, равно tд и . Этот факт был использован выше при выводе уравнения (103).

1.3.2.4. Эллиптические локальные участки поверхности Д И . Если главные кривизны k1.д и и k2.д и

имеют одинаковый знак, такой же знак имеет и текущая нормальная кривизна kд и во всех направлениях.

Это следствие того, что сечение поверхности Д И плоскостью, параллельной и близко расположенной к

касательной плоскости, является кривой, близкой к эллипсу. В пределе, когда расстояние между секущей и касательной плоскостями стремится к нулю, а масштаб изображения кривой их пересечения при этом

увеличивается до бесконечности, кривая сечения поверхности Д И в точности становится эллипсом.

Асимптотические линии	kд и 0 ,	проходящие через некоторую точку M на поверхности			Д И , в
этом случае отсутствуют (они мнимые) – круговая диаграмма не пересекает ось ординат (рис. 1.23.2).
1.3.2.5. Параболические	локальные	участки	поверхности	Д И . В особых случаях, когда	одна из
главных кривизн равна нулю	k1.д и 0,	k2.д и 0	или k1.д и	0, k2.д и 0 круговая диаграмма касается
оси ординат t (рис. 1.23.3).	Локальный участок поверхности			Д И в этом случае будет параболическим.

Название параболический происходит не потому, что его индикатриса кривизны является параболой – это не так. Индикатриса кривизны параболического локального участка поверхности Д И представляет собой пару

прямых, параллельных асимптотическому направлению. Название такого типа локального участка поверхности Д И происходит из аналогии с параболическим дифференциальным уравнением, которое

используется для описания особенностей локальной геометрии поверхности Д И в дифференциальной

окрестности параболической точки на ней.

В пределах локального участка параболического типа его можно рассматривать как параболический цилиндр – это также в некоторой мере объясняет происхождение названия локального участка поверхности

Д И рассматриваемого типа.

1.3.2.6. Гиперболические локальные участки поверхности Д И . Если первая главная кривизна k1.д и

положительна k1.д и 0 , а вторая k2.д и – отрицательна k2.д и 0 , имеем гиперболический локальный

участок гладкой регулярной поверхности Д И . Его индикатриса кривизны состоит из двух мнимых и двух

действительных ветвей гиперболы. Круговая диаграмма в этом случае имеет вид (рис. 1.23.4).

Для рассматриваемого случая можно указать две асимптотические прямые, для которых kд и 0 ; однако эти прямые не будут взаимно перпендикулярными до тех пор, пока главные кривизны k1.д и и k2.д и

не будут равны друг другу по модулю k1.д и k2.д и .

На рис. 1.23.4 показаны удвоенные величины углов между асимптотическими направлениями на поверхности Д И . Ось абсцисс kд и является биссектрисой этих углов. Отсюда можно заключить, что углы

между асимптотическими направлениями делятся линиями кривизны пополам.					Д И вырожда-
	Две асимптотические прямые для гиперболического локального участка поверхности
ются в одну прямую линию для параболического ее локального участка.
	1.3.2.7. Минимальные локальные участки поверхности			Д И . Если первая главная	кривизна k1.д и
положительна k1.д и 0 , а вторая k2.д и – отрицательна				k2.д и 0 и при этом выполняется условие
	k1.д и	k2.д и	, имеем минимальный локальный участок	гладкой регулярной поверхности Д И . Его

индикатриса кривизны состоит из двух мнимых и двух действительных ветвей гиперболы, которые зеркально- и центрально-симметричны. Круговая диаграмма в этом случае имеет вид (рис. 1.23.5).

1.3. О классификации рабочих поверхностей деталей и инструментов

1.3.2.8. Полная (гауссова), средняя и абсолютная кривизна локального участка поверхности

Д И .

Нормальная

кривизна

поверхности

r д и U д и , Vд и

в некотором направлении

t д и ,

где

д и

, находится как (Elber, G., Cohen, E., 1993):

д и

Φ2.д и

д и Lд и д и

kn.д и

(1.106)

д и

Φ1.д и

д и

д и Gд и д и

Нормальная кривизна зависит от направления касательной t д и

и равна радиусу кривизны окружности,

соприкасающейся к линии пересечения поверхности r д и U д и , Vд и

соответствующей нормальной секущей

плоскостью.

Нормальная кривизна является внутренним свойством поверхности и не зависит от вида ее параметризации. После дифференцирования (106) по д и , задача нахождения экстремальных значений

нормальной кривизны поверхности сводится к задаче нахождения корней уравнения:

l 2g

c 0 .

(1.107)

д и

n.д и

д и

n.д и

11 22

22 11

12 12

n.д и

Гауссова кривизна является произведением корней k1.д и и k2.д и уравнения (107)

k1.д и k2.д и

Lд и

Gд и

Произведение главных кривизн k1.д и и k2.д и

локального участка поверхности Д И равно его полной

кривизне:

(1.108)

Gд и k1.д и k2.д и .

Кривизну

К.-Ф. Гаусс назвал полной кривизной поверхности в заданной точке М на ней. Она

Gд и

является мерой формы локального участка поверхности

Д И ,

хотя с ее использованием связана некоторая

потеря информации по сравнению с использованием главных кривизн k1.д и и k2.д и раздельно.

Потеря этой информации может быть восстановлена введением в рассмотрение средней кривизны локального участка поверхности Д И в заданной точке на ней:

~	k1.д и k2.д и	g11l22	g22l11		2g12l12
Mд и						.
	2		2	Gд и
	2		2	Gд и
Как видим, обратные уравнения
			1
	~	~	~
	~	~	~
	k1.д и Mд и Mд2 и Gд и 2 ;

96	1. Рабочие поверхности деталей и инструментов.
	~	~ 2	~	1


	k2.д и Mд и Mд и Gд и
				2

указывают на то, что в этом случае потери информации о геометрии локального участка поверхности Д И

нет.							Д И
Из уравнения (108)		следует, что для эллиптических локальных участков поверхности						полная
кривизна положительна		~			~	0 , а для параболических –
		Gд и 0 , для гиперболических – отрицательна Gд и
равна нулю	~	Для любого		типа	локального участка поверхности	Д И координаты		центра
	Gд и 0 .
соответствующей круговой диаграммы будут					~
					Mд и ; 0 .		~
Для выпуклых локальных участков поверхности Д И средняя кривизна положительна
							Mд и 0 , для
вогнутых она отрицательна			~	и равна нулю для локальных участков уплощения и минимальных
			Mд и 0

локальных участков	~
	Mд и 0 .

Для эллиптических локальных участков поверхности Д И длина касательной, проведенной из начала

координат к круговой диаграмме, равна	~	(рис. 1.24.1). Этот результат очевиден из теоремы, дока-
	Gд и

занной в элементарной математике: квадрат касательной к окружности равен произведению секущей на ее

	внешнюю часть.	~
	Для локальных участков гиперболического типа длина полухорды вдоль оси ординат равна	~
		Gд и

(рис. 1.24.2).

Этот результат очевиден из теоремы, также доказанной в элементарной геометрии: если две хорды окружности пересекают одна другую под прямым углом, то произведения их частей равны друг другу. Это сразу приводит к теореме Эннепера, в соответствие с которой геодезическое кручение любой асимп-


тотической линии, проходящей через гиперболическую точку поверхности, равно			~
			Gд и .
Для локальных	участков	параболического типа гладких регулярных поверхностей Д И полная
кривизна равна нулю	~	. Это очевидно из уравнения (108), если рассматривать его с алгебраической
кривизна равна нулю	Gд и 0

точки зрения. К такому же результату придем с геометрических позиций, рассматривая круговую диаграмму параболического локального участка поверхности Д(И) как предельный случай аналогичных диаграмм для

эллиптического или для гиперболического локальных участков поверхности Д И .

Числитель в формуле	~	2Fд и Mд и Eд и Nд и Gд и Lд и						для расчета средней кривизны, и его
	Mд и
	Mд и	2(E	G		F	2	)
			д и	д и		д и

первые производные соответственно равны (Maekawa, T., Patrikalakis, N,. 1994):

Bд и 2Fд и Mд и Eд и Nд и Gд и Lд и ;

д и

2 Fд и

Uд и

Mд и

Uд и

Nд и Eд и

Uд и

Lд и Gд и

;

Uд и

д и

2 Fд и

Mд и

Nд и Eд и

Lд и Gд и

д и

1.3. О классификации рабочих поверхностей деталей и инструментов

Эллиптический

Средняя

кривизна

Mд и

вогнутый

tд и

выпуклый

локального участка поверхности

Д И

просто находится по его

круговой диаграмме.

Поскольку

центр окружности всегда распо-

G д и

ложен на середине ее диаметра,

средняя

кривизна

будет

k2.д и

k1.д и

kд и

Mд и

k1.д и

kд и

k2.д и

равна

среднему

значению

из

двух нормальных кривизн, изме-

ренных в двух взаимно перпен-

Гиперболический

дикулярных направлениях.

Для

этого не обязательно определять

псевдовогнутый

псевдовыпуклый

сначала главные кривизны по-

tд и

верхности

Д И .

Обратим вни-

мание

на

то,

что соответству-

ющее

утверждение

не

будет

G д и

1.д и

справедливым в отношение гаус-

совой

кривизны

локального

k2.д и

kд и

k2.д и

kд и

участка

поверхности

Д И . В

этом легко убедиться из геоме-

трической

интерпретации

сред-

ней

и полной

кри-

Mд и

Gд и

Рис. 1.24. Геометрическая интерпритация полной (гауссовой) кривизны

визны

поверхности

Д И

по

локального участка поверхности

Д(И) .

круговой

диаграмме

поверхно-

сти. Из рис. 1.25 следует, что

д и

OD OE OC2 CD2

д и

но CD изменяется при изменении величины угла , тогда как величина OC постоянна.

1.3.2.9. Построение круговой диаграммы локального участка поверхности

Д И .

Достаточно знать

координаты двух разных точек круговой диаграммы локального участка поверхности

Д И ,

чтобы

определить ее однозначно.

Кривизна kд и и

кручение tд и для касательных направлений

r д и

расчитаны путем под-

Uд и

Vд и

становки h 0 и

0 соответственно в уравнения:

д и

h h2

kд и

д и

;

Eд и 2Fд и h Gд и h2

д и

h F

д и

tд и

д и

Hд и Eд и 2Fд и h Gд и h2

д и

получим две точки

д и

;

д и

д и д и

;

д и

1. Рабочие поверхности деталей и инструментов.

Этот результат может быть переписан в форме

kд и

д и

Mд и Fд и U

д и

Fд и V

Mд и

;

д и

Uд и

Hд и

Vд и

Hд и

где

kд и

Lд и

kд и

Nд и

Uд и

Eд и

Vд и

Gд и

Использование круговых диаграмм позволяет дать наглядную геометрическую интерпретацию характера взаимосвязи между локальными участками разного типа гладких регулярных локальных участков поверхно-

стей Д И при изменении величин, соотношений и знаков их главных кривизн.

Проследим какие изменения проис-

ходят с локальным участком поверхности

tд и

Д И ,

если в системе координат

kд и tд и

(рис. 1.26.1) перемещаться справа от ди-

аграммы выпуклого эллиптического локаль-

ного участка влево к вогнутому эллипти-

ческому

локальному

участку

обратно

k2.д и

k1.д и

(рис. 1.26.2).

Образующиеся

при

этом

различные

kд и

типы

локальных

участков

поверхности

Д И

удобно расположить

по

периметру

окружности,

например,

по

ходу

часовой

P kд и ,tд и

стрелки. В результате придем к таким

схемам

расположения

круговых

диаграмм

(рис. 1.27), индикатрис кривизны (рис. 1.28)

OC CD

и собственно локальных участков (рис. 1.29)

OC CE

гладких регулярных поверхности

Д И .

Приведенные результаты (см. рис. 1.27

( ) k

( 90 ) OD OE OC2 CD2

– рис. 1.29)

наглядно иллюстрируют транс-

д(и)

формацию

различного

типа

локальных

OC CD

участков

гладкой регулярной

поверхности

Д И

из одного в другой. Эти

схемы

Рис. 1.25. К построению круговой диаграммы

взаимно дополняют друг друга и позволяют

поверхности

Д(И) .

выразительнее представить

классификацию

гладких

регулярных

локальных

участков

сложных поверхностей деталей и инструментов (табл. 1.1), разработанную ранее (Радзевич С.П., 1988). Введение в рассмотрение круговых диаграмм позволяет однозначно определиться с тем, что одна из

главных кривизн (а именно первая k1.д и ) больше другой алгебраически и нет необходимости в рассмотрении

соотношений их абсолютных величин. Становится ясным взаимосвязь между различного типа локальными участками поверхностей Д И и порядок рассмотрения особенностей их локальной геометрии: логично это

делать, рассматривая перемещение круговой диаграммы вдоль оси абсцисс справа налево и в обратном направлении, что хорошо видно при рассмотрении рис. 1.26 совместно с рис. 1.27 – рис. 1.29. При этом также рассматриваются круговые диаграммы разного радиуса, в том числе и вырождающиеся в точку, что имеет

место для омбилических локальных участков поверхности Д И и их локальных участков уплощения. Это

также хорошо иллюстрируется схемами с расположением круговых диаграмм (рис. 1.27), индикатрис кривизны (рис. 1.28) или схем локальных участков поверхностей Д И (рис. 1.29) по окружности единичного

радиуса.

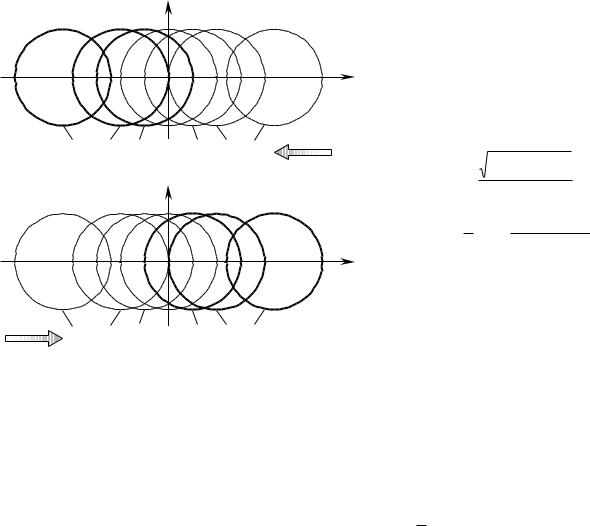
1.3. О классификации рабочих поверхностей деталей и инструментов

tд и

Рассматривая

локальные

участки

поверхностей

Д И ,

их

форму

можно

определять не только через главные криви-

зны k1.д и

k2.д и ,

но и через среднюю

и так называемый индекс

kд и

кривизну Mд и

формы

Sд и . Эти параметры можно рас-

считать так (Koenderink, J.J., 1990):

1.д и

2.д и

tд и

Mд и

;

2 arctan k1.д и k2.д и .

д и

k1.д и k2.д и

kд и

Индекс формы

Sд и

рассматривается

как мера “формы”,

средняя кривизна

– как мера размера. Например, все

Mд и

сферы разного радиуса имеют одинаковый

индекс формы, но разную среднюю кривиз-

ну.

Рис. 1.26. Расположение круговых диаграмм для различного

За

исключением

локального

участка

уплощения, каждому отдельному локаль-

типа локальных участков гладких регулярных

ному участку поверхности

Д И

соответ-

поверхностей

Д(И) .

ствует единственное значение индекса фор-

мы. Положительному значению индекса

формы соответствуют выпуклые локальные участки поверхностей Д И , а отрицательному – вогнутые.

Интересные результаты дополнительно могут быть получены, если вместо средней кривизны Mд и

поверхности Д И рассматривать ее “искривленность”, равную

Cд и

ln Mд и . Это позволяет исключить

из рассмотрения масштабный фактор. В таких координатах все формы отображаются на ленту бесконечной

длины в Cд и направлении (Koenderink, J.J., 1990).

На параметры

Sд и

можно смотреть как на полярные координаты в плоскости, когда началу

Mд и и

системы координат соответствует локальный участок уплощения. При таком подходе на окружности, по

периметру которой расположены различные типы локальных участков поверхностей

Д И

(см. рис. 1.27 –

рис. 1.29) можно смотреть как на окружности единичного радиуса – средняя кривизна постоянна, изменяется

только индекс формы.

Таким образом для описания локальной геометрии поверхностей Д И можно использовать различные

меры кривизны:

k1.д и и k2.д и – главные кривизны;	~
k1.д и и k2.д и – главные кривизны;	Mд и – средняя кривизна;
~	~
Aд и – абсоютная кривизна;	Gд и – полная (гауссова) кривизна;
Cд и – искривленность;	Sд и – индекс формы.

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 6010 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете Технология машиностроения

#
23.02.202324.47 Mб11Radzevich, S.P. Monograph - 2001.pdf
#
23.02.20237.23 Mб4Горбацевич - Курсовое проектирование по ТМ.doc
#
23.02.2023949.47 Кб3Мешкова - Организация Технологии Отрасли.pdf
#
23.02.20234.4 Mб1Оптимизация Технологических Систем (укр).pdf
#
23.02.2023882.47 Кб3Основные Положения Теории Базирования (Лекции).pdf
#
23.02.20231.01 Mб6Основы Проектирования ТП.pdf