Добавил:

Mehanik Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Технический Университет им. Р.Е. Алексеева

Предмет:

Технология машиностроения

Файл:

Radzevich, S.P. Monograph - 2001

.pdf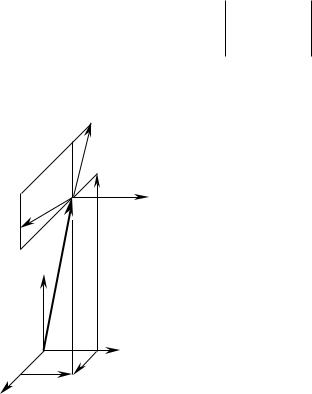

Скачиваний:

Добавлен:

23.02.2023

Размер:

24.47 Mб

Скачать

☆

<<< < Предыдущая 6 7 8 9 10 11 12 13 14 15 16 1718 / 6018 19 20 21 22 23 24 25 26 27 28 29 30 > Следующая >>>

170

3. Системы координат и линейные преобразования

где Rs 1 2 –

оператор результирующего преобразования координат, имеющий следующее матричное

представление:

a11

a12

a13

a14

Rs 1 2

a21

a22

a23

a24 .

a31

a32

a33

a34

Левый верхний блок порядка 3 3 описывает поворот новой системы координат

X2Y2 Z2 относительно

своего начала координат в такое положение, в котором оси этой системы располагаются параллельно

соответствующим осям исходной системы координат

X1Y1Z1

и одинаково направлены с ними. Отсюда

следует, что этот блок представляет собой ортогональную матрицу, т.е. для всех i, k 1, 2, 3

если

i k;

aij akj a ji a jk

если

i k

j 1

и, кроме того, определитель этой матрицы

a11

a12

a13

a21

a22

a23

1 .

a31

a32

a33

Три

первые

координаты a14 ,

a 24 ,

a34 четвертого столбца

оператора Rs 1 2

результирующего

преобразования координат представляют собой декартовы координаты

начала

новой

системы

координат

X2Y2 Z2

исходной

системе

координат X1Y1Z1 .

Оператор

Rs 1 2 результирующего преобразования координат

может быть получен так.

Рассмотрим две системы координат X1Y1Z1

X2Y2 Z2

(рис. 3.8).

Положение некоторой точки M в исходной системе координат

X1Y1Z1

определяется радиус-вектором

X M

Y M

1 T .

X2(O1 )

Положение этой же точки M в системе координат X2Y2 Z2

может

быть определено радиус-вектором r

X M

Y M

1 T .

Справедливо соотношение r 2 Rs 1 2 r1 . Оператор Rs m n

преобразования координат составляется так:

a11

a12

a13

a14

Y(O1 )

a22

a23

(O )

Rs 1 2

a32

a33

a42

a43

Рис. 3.8. К выводу матрицы пре-

a41

образования оординат.

											3.4. Преобразования декартовых систем координат																											171
i	2	i	1	i	2	j	1	i	2	k	1	l i	2	cos X		2	,X		cos X			,Y			cos X			,Z			X		O1
	2		1		2		1		2		1		2			2		1				2 1						2 1					2
j	2 i1			j 2 j1				j 2 k 1				l j 2		cos Y ,X					cos Y ,Y						cos Y ,Z						Y O1
															2			1			2		1				2		1			2			.		(3.14)
	2 i1			k 2 j1				k 2 k 1				l k							cos Z2 ,Y1						cos Z2 ,Z1						Z		O		.		(3.14)
k	2 i1			k 2 j1				k 2 k 1				l k	2	cos Z2 ,X1					cos Z2 ,Y1						cos Z2 ,Z1						Z		1
		0				0				0		1			0						0						0						2
															0						0						0						1
Здесь l		– вектор, направленный из O2 в O1														l		O2O1		; i 2 ,			j 2 , k 2 – орты новой системы координат
X2Y2 Z2 , а i1 ,			j1 ,	k 1 – орты исходной системы координат																X1Y1Z1 ;				O1	и O2		– начала исходной X1Y1Z1 и
новой X2Y2 Z2			систем координат.
Использование однородных координат позволяет унифицировать математические действия при
многократных преобразованиях координат, с чем часто приходится сталкиваться при решении задач
формообразования поверхностей деталей.
Операторы результирующих преобразований координат можно представить как произведения
относительно простых операторов последовательных преобразований координат (табл. 3.1). Следует помнить,
что порядок матриц в произведениях имеет существенное значение.
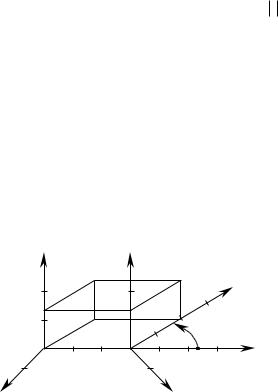
Пример 3.6. Пусть новая система координат													X2Y2Z2 получена в результате поворота исходной системы координат																								X1YZ1 1	на угол
30 вокруг оси Z1			и смещения на вектор 0									3	0	1 T (рис.	3.9). Такое преобразование координат описывается оператором Rs 1 2
результирующего преобразования координат:
																														0,866			0,5			0	0
																		Rs 1 2 Rt 30 , Z1 Tr 3, Y1
Z							Z	2										Rs 1 2 Rt 30 , Z1 Tr 3, Y1													0,5		0,866			0	3 .
1								2				А		Y2
												А		Y2																	0			0		1	0
																															0			0		0	1
2								2				3
2								2				3
1											2
1										1		30		Y				Координаты некоторой точки M ,												заданные в исходной системе
														Y																r M		0					1 T , в
0														1				координат X YZ						радиус-вектором						r M		0			1	1	1 T , в	новой
																					1 1		1							1
1			1			2		3		4		5		6				системе		координат				X2Y2Z2		выражаются						радиус-вектором						r2 M ,
X1										X2								равным:
Рис. 3.9. Пример преобразования координат при переносе																										0,866			0,5				0	0		0	0,5
Рис. 3.9. Пример преобразования координат при переносе
начала системы координат, совмещенного с поворо-																		r	M Rs 1 2 r M								0,5		0,866				0	3		1	3,866 .
том вокруг оси аппликат (Marciniak, K, 1991).																			2						1		0			0			1
том вокруг оси аппликат (Marciniak, K, 1991).																											0			0			1	0		1	1
																										0				0			0	1 1			1

При использовании однородных координат обратное преобразование координат требует нахождения
оператора обратного преобразования координат Rs 2 1 ,																			который равен обратному оператору Rs 1 1 2
прямого преобразования координат, т.е.													Rs 2 1 Rs 1 1 2 . Если
															a			a		a	a
															11			12		13		14
												Rs 1 2			a21			a22		a23 a24 ,
															a31			a32		a33	a34
																		0		0
															0			0		0		1
а элементы матрицы обратного преобразования координат обозначены через bik :

172						3. Системы кооринат и линейные преобразования
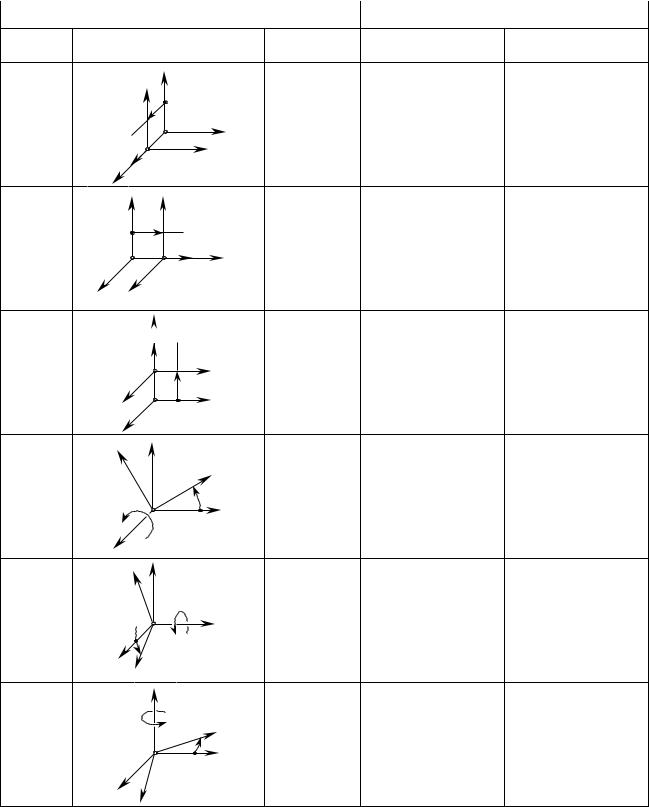
					Операторы преобразования правых систем координат													Таблица 3.1
																		Таблица 3.1
			Преобразования координат					Описание оператора преобразования координат
действие				схема			обозначение	в матричной форме							системой уравнений
действие				схема			оператора	в матричной форме							системой уравнений
							оператора
перенос				Z1
вдоль	оси			Z1					1	0	0	d x
X на dx			Z2						1	0	0	d x			X			X d		;
X на dx			Z2			Y			0	1	0	0			X		2	X d	x	;
						Y	Tr (dx, X)		0	1	0	0					2	1	x
			d x			1	Tr (dx, X)			0	1	0			Y2 Y1;
			d x						0	0	1	0			Z			Z .
															Z	2		Z .
									0	0	0	1				2		1
			X2	X1		Y2			0	0	0	1
			X2	X1		Y2
перенос			Z1	Z2
вдоль	оси		Z1	Z2	d y				1	0	0	0			X2 X1;
Y на d y									1	0	0	0
Y на d y
							Tr (d y ,Y)		0 1		0 d y				Y2 Y1 d y ;
									0	0	1	0			Z2 Z1.
			X1		Y	Y				0	0	1			Z2 Z1.
			X1	X2	1	2			0	0	0	1
				X2
перенос				Z2
вдоль	оси			Z2					1	0	0	0
вдоль	оси				dz
Z на d															X			X ;
Z на d		z		Z1											X		2	X ;
		z		Z1													2	1
						Y	Tr (dz , Z)		0 1		0	0			Y2 Y1;
			X2			Y			0	0	1	d z
						2									Z2 Z1 d z.
										0	0	1			Z2 Z1 d z.
			X1			Y			0	0	0	1
			X1			1
поворот				Z1
вокруг			Z2	Z1				1		0		0		0	X2 X1;
оси X на			Z2		Y2				cos			sin			X2 X1;
угол							Rt ( , X)	0	cos			sin		0	Y2 Y1 cos Z1 sin ;
угол							Rt ( , X)	0	sin			cos		0	Y2 Y1 cos Z1 sin ;
															Z2 Y1 cos Z1 sin ;
						Y		0		0		0		1
			X1	X2		1
			X1	X2
поворот					Z1
вокруг			Z2		Z1			cos		0	sin			0
оси Y на			Z2					cos		0	sin			0	X2 X1 cos Z1 sin ;
оси Y на															X2 X1 cos Z1 sin ;
угол						Y2	Rt ( ,Y)		0	1		0		0	Y Y ;
						Y		sin		0	cos			0	2			1
			X1			Y									Z	2		X sin Z cos .
			X1			1			0	0		0				2		1		1
				X2					0	0		0		1
				X2
поворот				Z1	Z2
вокруг				Z1	Z2	Y2		cos			sin		0	0
оси Z		на				Y2					cos		0		X2 X1 cos Y1 sin ;
угол								sin			cos		0	0	X2 X1 cos Y1 sin ;
угол							Rt ( , Z)		0		0		1	0	Y2 X1 sin Y1 cos ;
							Rt ( , Z)		0		0		1	0	Y2 X1 sin Y1 cos ;
			X			Y					0				Z2 Z1.
			X			Y		0			0		0 1		Z2 Z1.
			1	X2		1
				X2

3.4. Преобразования декартовых систем координат										173
		b		b	b	b
			11	12	13	14
Rs 2 1		b21 b22			b23	b24	,
		b		b	b	b
			31	32	33	34
			0	0	0	1
то
	1				1	Aik
Rs 2 1 B Rs		1 2 aik							,	(3.15)
Rs 2 1 B Rs		1 2 aik				det a		ik	,	(3.15)
								ik

где Aik алгебраическое дополнение элемента aik в определителе det aik . Вследствие ортогональности минора

a11 a12a21 a 22a31 a32

a13 a23 a33

оператора Rs 1 2 прямого преобразования координат процедура нахождения оператора	Rs 2 1
обратного преобразования координат существенно упрощается:

b	b	b	a	11	a	12	a	13	T	a	11	a	21
11	12	13		11		12		13			11		21
b21	b22	b23	a21		a22		a23			a12		a22
b	b	b	a	31	a	32	a	33		a	13	a	23
31	32	33		31		32		33			13		23

a31 a32 . a33

Оставшиеся элементы b14 , b24 , b34 матрицы Rs 2 1 обратного преобразования координат могут быть получены по формуле (15), используя которую, находим:

b14 a11a14 a21a24 a31a34 ; b24 a12 a14 a22 a24 a32 a34 ; b34 a13a14 a23a24 a33a34 .

В конечном итоге можно записать, что

a11

a21

a31

a11a14

a 21a24

a31a34

Rs 2 1

a13

a23

a33

a13a14

a23a24

a33a34

Если оператор Rs 1 2 результирующего преобразования координат представить в виде:

a11	a12	a13	a14	a x	bx	cx	d x

Rs 1 2 a 21	a 22	a 23	a 24	a x	by	c y	d y	,
a31	a32	a33	a34	a y	bz	cz	d z
	0	0			0	0
0	0	0	1	0	0	0	1

174	3. Системы координат и линейные преобразования

оператор Res 2 1 обратного преобразования координат записывается так:

a x	a y	a z	d a

Rs 2 1 bx	by	bz	d b	,
cx	cy	cz	d c
	0	0
0	0	0	1

где a a xi a y j a zk ,	b bxi by j bzk , c cxi c y j czk					и d d xi d y j d zk .
Пример 3.6. (продолжение). Оператор Re 2 1		обратного результирующего преобразования координат (от новой X2Y2Z2 к
исходной X1YZ1 1 ) имеет вид:
			0,866			0,5	0	1,5
	Rs 2 1 Rs	1 1 2
	Rs 2 1 Rs	1 1 2		0,5	0,866		0	2,595 .
				0		0	1	0
				0		0	0	1
				0		0	0	1

Для описания многократных n кратных последовательных преобразований координат достаточно воспользоваться формулой

(3.16) r	Rs n 1 n Rs n 2 n 1 Rs 1 2 r		n
(3.16) r	Rs n 1 n Rs n 2 n 1 Rs 1 2 r			Rs n i n i 1 r ,
2		1
2		1		1
			i 1

которая представляет собой произведения матриц частных последовательных преобразований координат вида

(14) и (табл. 3.1).

Следует еще раз подчеркнуть, что в общем случае порядок перемножения матриц в (16) имеет

существенное	значение.	Операторы Tr d x , X , Tr		d y , Y , Tr d z , Z ,	Rt , X , Rt , Y и	Rt , Z
последовательных переносов вдоль и поворотов вокруг осей системы координат XYZ входят в (16) как
вырожденные	случаи	некоторого	оператора	результирующего	преобразования	координат

Rs n i 1 n i , когда он описывает единственное смещение вдоль или только поворот вокруг одной из

осей системы координат XYZ .

3.4.5. Правые и левые системы координат. Изменение направленности систем координат. В мате-

матике вообще и в геометрии в частности принято использовать левые системы координат. При программировании обработки сложных поверхностей деталей на многокоординатных станках с ЧПУ общепринятым является использование правых систем координат металлорежущего станка.

Преобразование правой системы координат в левую и обратно производится при помощи операторов отображения.

Чтобы изменить направление оси абсцисс на противоположное, т.е. чтобы для новой X2Y2 Z2 и исходной X1Y1Z1 систем координат справедливыми были соотношения X2 X1 , Y2 Y1 и Z2 Z1 , достаточно воспользоваться оператором Rf Y1Z1 отображения относительно плоскости координат Y1Z1 :

	1		0	0	0
Rf Y Z
Rf Y Z		0	1	0	0 .
1 1		0	0	1	0
			0	0
	0		0	0	1

3.5. Влияние преобразований координат на основные квадратичные формы							175
поверхности детали и исходной инструментальной поверхности
Изменение направления оси ординат на противоположное (т.е. чтобы для новой X2Y2 Z2							и исходной
X1Y1Z1 систем координат справедливыми были соотношения				X2 X1 , Y2 Y1	и	Z2 Z1 ) производится
оператором Rf X1Z1 отображения относительно плоскости координат X1Z1 :
	1	0	0	0
		1
Rf X Z 0		1	0	0 .
1 1	0	0	1	0
		0	0
	0	0	0	1
Чтобы изменить направление оси аппликат на противоположное, т.е. чтобы для новой X2Y2 Z2 и станой
X1Y1Z1 систем координат справедливыми были соотношения				X2 X1 , Y2 Y1	и	Z2 Z1 ,	достаточно
воспользоваться оператором Rf X1Y1 отображения относительно плоскости координат X1Y1 :
	1	0	0	0
Rf X Y
Rf X Y	0 1 0			0 .
1 1	0	0	1	0
		0	0
	0	0	0	1

При каждом из таких преобразований правая система координат становится левой или наоборот.

3.5.Влияние преобразований координат на основные квадратичные формы поверхности детали и исходной инструментальной поверхности

При решении задач формообразования поверхностей деталей производятся многократные преобразования координат. Это приводит к тому, что уравнение поверхности Д И изменяется. Поэтому

коэффициенты первых двух основных квадратичных форм форм Φ1.д и и Φ2.д и поверхности Д И следует

находить заново. Избежать необходимости многократного выполнения этой рутинной операции можно путем использования операторов преобразования координат. Коэффициенты первых двух основных квадратичных форм, найденные в одной системе координат, в этом случае могут быть использованы, когда поверхность

Д И определена в другой системе координат или иначе параметризована. Эти факторы учитываются путем

применения операторов преобразования координат и якобиана преобразования параметров при определении коэффициентов квадратичных форм Φ1.д и и Φ2.д и .

Поэтому важным является вопрос о влиянии преобразований координат на основные квадратичные формы Φ1.д и и Φ2.д и поверхности Д И .

Рассмотрим случай когда поверхность Д И задана уравнениями в параметрической форме (1.1):

Xд и Xд и Uд и ,Vд и ;

Yд и Yд и Uд и ,Vд и ;

Zд и Zд и Uд и ,Vд и .

Первая основная квадратичная форма Φ1.д и поверхности

Д И , определяющая метрику поверхности,

записывается в форме (1.23):

д и

dU dV

dV2

1.д и

д и

176

3. Системы координат и линейные преобразования

Вторая основная квадратичная форма Φ2.д и поверхности

Д И , определяющая кривизну поверхности

и ее кручение, записывается так (1.35):

2.д и

д и

d 2r

д и

L dU

dV2

д и

Третья Φ3.д и и четвертая

Φ4.д и

квадратичные формы поверхности

Д И выражаются через первые

две ее основные квадратичные формы Φ1.д и и Φ2.д и .

Для удобства каждую из обрабатываемых поверхностей детали и каждый отдельный участок ИИП И

задают в своих системах координат, связанных с соответствующей поверхностью Д И . По этой причине, а

также вследствие того, что в задачах формообразования часто применяют и другие системы координат, необходимо приведение уравнений каждого участка поверхности Д И к некоторой общей для всех системе

координат. Для этого удобно уравнения поверхности Д И представлять в матричной форме (в виде матриц-

столбцов): r	д и	X	д и	Y	Z	д и	1 T , а преобразования координат производить при помощи оператора
	д и		д и	д и		д и

Rs 1 2 результирующего преобразования координат (14):

cos X1 X2

(3.17) Rs 1 2 cos X1Y2

cos X1Z20

cos Y1 X2 cos Y1Y2 cos Y1Z2 0

cos Z1 X2 cos Z1Y2 cos Z1Z2 0

d x d y .

d z

		Чтобы		получить		уравнение поверхности			Д И в новой системе	координат, матрицу-столбец
r	д и	X	д и	Y	Z	д и	1 T	следует умножить слева на оператор Rs 1 2 :
	д и		д и	д и		д и
								rд и Rs 1 2 rд и .
								2	1
		Очевидно, что уравнение поверхности Д И							в новой системе координат	X2Y2 Z2 будет отличаться от

исходного уравнения этой же поверхности, заданной в исходной системе координат X1Y1Z1 . По этой причине изменится и форма описания первых двух основных квадратичных форм Φ1.д и и Φ2.д и поверхности Д И . Очевидно, что используя уравнения (1.47) и (1.48)-(1.50), можно рассчитать гауссовы коэффициенты первых двух основных квадратичных форм для уравнения rд и 2 Xд и Yд и Zд и 1 T в новой системе

координат X2Y2 Z2 .

Любая квадратичная форма допускает матричное представление. Квадратичные формы Φ1.д и и Φ2.д и в матричном виде представляются так:

									Eд и		Fд и	0	0	dUд и
	Φ			dU
(3.18)	Φ			dU		д и	dV	0	1 Fд и		Gд и	0	0 dVд и ;
		1.д и				д и	д и			0	0	1	0		0
										0	0	0			1
										0	0	0	1		1
									Lд и		Mд и	0	0	dUд и
	Φ		dU
(3.19)	Φ	2.д и	dU		д и		dV	0	1 Mд и		Nд и	0	0	dVд и .
		2.д и			д и		д и			0	0	1	0		0
										0	0	0			1
										0	0	0	1		1

3.5. Влияние преобразований координат на основные квадратичные формы	177
поверхности детали и исходной инструментальной поверхности

По правилу перемножения матриц произведение второго и третьего сомножителей в (18) и в (19) является столбцовой матрицей, а произведение матрицы-строки (первого сомножителя) на столбцовую

матрицу произведения второго и третьего сомножителей равно матрице первого порядка, т.е. числу Φ1.д и

или Φ2.д и .

В результате преобразования координат столбцовая матрица переменных в (18) и в (19) преобразуется к

виду

dUд и		dUд и
	2		1
dVд и 2		Rs 1 2 dVд и 1		.
	0		0
	1		1
	1		1

Подставив это выражение в (18) и в (19), получим

		dUд и				T	Eд и					Fд и				0	0		dUд и
Φ1.д и				1					F		1	G			1	0	0				1
				dV					F	д и 1		G	д и		1	0	0	Rs 1 2		dV
	Rs 1 2			д и 1						д и 1			д и		1	1		Rs 1 2			д и 1		;
2				0							0			0		1	0				0

				1			0							0		0	1				1
				1			0							0		0	1				1
		dUд и			T				Lд и			Mд и				0	0			dUд и
Φ2.д и				1				M			1	N			1	0	0				dV	1
		2	dV					M			д и 1	N		д и 1		0	0		Rs 1 2		dV		.
	Rs 1	2		д и 1							д и 1			д и 1		1			Rs 1 2		д и 1		.
2				0							0			0		1	0				0

				1			0							0		0	1				1
				1			0							0		0	1				1

По правилу транспонирования произведения имеем:

					dUд и				T					dUд и T

			Rs		1 2 dVд и					Rs T 1 2 dVд и							.
							0								0		.
							0								0
							1								1


Следовательно
		dUд и		T				Eд и			Fд и			0 0				dUд и
			1					F		1	G		1	0 0					1
Φ1.д и		dV						F		д и 1	G	д и 1		0 0				dV
Φ1.д и			д и 1		RsT 1		2			д и 1		д и 1			Rs 1 2				д и 1		.
	2		0					0					0	1 0					0


			1					0					0	0 1					1
			1					0					0	0 1					1
																						(3.20)
		dUд и T							Lд и		Mд и			0 0				dUд и
			1					M		1	N		1	0 0				dV		1
Φ2.д и		dV						M		д и 1	N		д и 1	0 0				dV
Φ2.д и			д и 1		Rs T 1	2				д и 1			д и 1			Rs 1 2			д и 1			.
	2		0							0			0	1 0					0


			1							0			0	0 1					1
			1							0			0	0 1					1

178				3. Системы координат и линейные преобразования
В уравнениях (20) матрицы в круглых скобках
Eд и		Fд и	0	0			Lд и		Mд и	0	0
					Rs 1 2							Rs 1 2
RsT 1 2 Fд и		Gд и	0	0	Rs 1 2	и	RsT 1 2 Mд и		Nд и	0	0	Rs 1 2
	0	0	1	0				0	0	1	0
		0	0						0	0
0		0	0	1			0		0	0	1

симметричны, а столбцовая матрица
dUд и
	1
dVд и 1
	0
	1
	1

составлена из переменных dUд и 1 и dVд и 1 . Поэтому (20) является квадратичной формой относительно этих

величин.

Если заданная в исходной системе координат X1Y1Z1 поверхность Д И имеет квадратичные формы Φ1.д и 1 или Φ2.д и 1 с матрицами соответственно

		Eд и		Fд и			0 0					Lд и			Mд и	0 0
			1		1		0 0				Mд и		1		1	0 0
		Fд и		Gд и			0 0		и		Mд и				Nд и	0 0
			1	0	1				и			0	1		1	,
			0	0			1 0					0			0	1 0
				0								0			0
		0		0			0 1					0			0	0 1
то после перехода к новой системе координат								X2Y2 Z2 ,		в новых переменных эти квадратичные формы будут
иметь матрицы
								Eд и			Fд и	0 0
			Φ1.д и						1		1
			Φ1.д и		RsT 1 2 Fд и 1						Gд и 1	0 0		Rs 1 2 ;
				2					0		0	1	0
									0		0	0
									0		0	0	1
(3.21)
									Lд и		Mд и	0 0
									1		1
			Φ2.д и RsT 1 2 Mд и 1								Nд и 1	0 0			Rs 1 2 .
				2					0		0	1	0
									0		0	0
									0		0	0	1
Квадратичные формы Φ1.д и и Φ2.д и в исходной										X1Y1Z1		и новой			X2Y2 Z2	системах координат имеют
различные коэффициенты. При этом необходимо помнить, что одна и та же точка M поверхности Д И в
исходной системе координат				X Y Z			имеет координаты				X M ,	Y M ,			Z M , а в новой – свои координаты
				1	1	1					1	1			1
X M	, Y M , Z	M . Координаты			X	M , Y M		, Z M и		X	M , Y M ,		Z	M связаны между собой оператором
2	2	2			1		1	1			2	2		2

(17) результирующего преобразования координат.

3.6. Косоугольные системы координат

179

Использование соотношений (21) и (22) для перерасчета первых двух основных квадратичных форм Φ1.д и и Φ2.д и поверхности Д И после преобразования координат заметно упрощает расчеты и

способствует получению точных и надежных результатов.

В общем случае после каждого преобразования координат коэффициенты Eд и , Fд и , Gд и и Lд и , Mд и , Nд и первых двух основных квадратичных форм Φ1.д и и Φ2.д и поверхности Д И изменяются.

Гауссовы коэффициенты инвариантны относительно только переноса начала координат, когда поворот осей координат отсутствует – это однозначно следует из структуры формул (1.47) и (1.48)-(1.50) для расчета

коэффициентов Eд и , Fд и , Gд и и Lд и , Mд и , Nд и . Перенос начала координат приводит к появлению

новых констант, которые исчезают после первого дифференцирования, тогда как структурные изменения формул для расчета этих же коэффициентов при повороте осей координат более существенны.

3.6. Косоугольные системы координат

Косоугольные системы координат встречаются при решении задач формообразования сложных поверхностей деталей на многокоординатных станках с ЧПУ. Например, подвижный репер с началом на

поверхности Д И , с двумя осями, касательными к координатным линиям на поверхности, и третьей осью, направленной по нормали к поверхности Д И , в общем случае неортогональны. Поэтому необходимо либо

уметь по заданному косоугольному базису строить ортогональный, либо преобразовывать косоугольные координаты.

3.6.1. Базисы косоугольных систем коориднат. Координаты вектора зависят от выбора базиса. Пусть

некоторый вектор r

в исходном базисе i1 ,

j1 ,

k 1

имеет координаты rx ,

ry ,

rz , а в новом базисе i 2 , j2 ,

k 2

– координаты

(рис. 3.10).

Установим связь между координатами одного и того же вектора в этих базисах i1 , j1 , k 1 и i 2 , j2 , k 2 . Выразим новые базисные векторы в исходном базисе (Клиот-Дашинский М.И., 1974). Обозначив

координаты вектора i2	в исходном базисе через t11 , t12 , t13 , координаты вектора j2	– через t21 , t22 , t23 , а
координаты вектора k 2	– через t31 , t32 , t33 , получим
	i2 t11i1 t12 j1 t13k 1 ;
	j2 t21i1 t22 j1 t23k 1 ;	(3.22)
	k 2 t31i1 t32 j1 t33k 1 .

Коэффициенты правых частей этих равенств образуют матрицу

t11 t12T t21 t22

t31 t32

t13 t23 . t33

Эта матрица неособенная, т.к. при D T 0 не существует обратной матрицы T T , а это означает, что исходные базисные векторы не могут быть выражены в виде линейных комбинаций векторов i 2 , j2 , k 2 . Последнее утверждение противоречит предположению, что система i1 , j1 , k 1 образует базис трехмерного

пространства.

Неособенная матрица M1 2 , транспонированная по отношению к матрице T :

<<< < Предыдущая 6 7 8 9 10 11 12 13 14 15 16 1718 / 6018 19 20 21 22 23 24 25 26 27 28 29 30 > Следующая >>>

Соседние файлы в предмете Технология машиностроения

#
23.02.202324.47 Mб11Radzevich, S.P. Monograph - 2001.pdf
#
23.02.20237.23 Mб4Горбацевич - Курсовое проектирование по ТМ.doc
#
23.02.2023949.47 Кб3Мешкова - Организация Технологии Отрасли.pdf
#
23.02.20234.4 Mб1Оптимизация Технологических Систем (укр).pdf
#
23.02.2023882.47 Кб3Основные Положения Теории Базирования (Лекции).pdf
#
23.02.20231.01 Mб6Основы Проектирования ТП.pdf

b	b	b	a	11	a	12	a	13	T	a	11	a	21
11	12	13		11		12		13			11		21
b21	b22	b23	a21		a22		a23			a12		a22
b	b	b	a	31	a	32	a	33		a	13	a	23
31	32	33		31		32		33			13		23

b	b	b	a	11	a	12	a	13	T	a	11	a	21
11	12	13		11		12		13			11		21
b21	b22	b23	a21		a22		a23			a12		a22
b	b	b	a	31	a	32	a	33		a	13	a	23
31	32	33		31		32		33			13		23

b	b	b	a	11	a	12	a	13	T	a	11	a	21
11	12	13		11		12		13			11		21
b21	b22	b23	a21		a22		a23			a12		a22
b	b	b	a	31	a	32	a	33		a	13	a	23
31	32	33		31		32		33			13		23