Radzevich, S.P. Monograph - 2001

Г л а в а 3. Системы координат и линейные преобразования

Для решения задачи синтеза наивыгоднейшего формообразования поверхности детали используются различные системы координат и соответствующие линейные преобразования. Применение находят системы координат следующих видов: прямоугольные и косоугольные декартовы, однородные, цилиндрические, сферические и другие криволинейные системы координат. Линейные преобразования в основном связаны с преобразованием аналитического описания геометрических образов детали и инструмента, заданных в различных системах координат.

3.1. Используемые системы координат

При разработке технологии формообразующей обработки первичной является деталь. Тело детали ограничено рядом поверхностей. Каждая отдельно взятая поверхность аналитически описывается в некоторой системе координат. Степень сложности аналитического представления геометрической информации об обрабатываемой поверхности Д и о детали целиком зависит от выбора системы координат, в которой

описывается как конкретная поверхность Д , так и вся деталь.

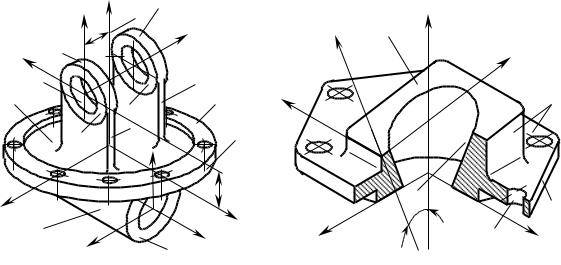
Для аналитического описания рабочих поверхностей деталей удобно вводить в рассмотрение системы координат X1Y1Z1 , X2Y2 Z2 , , XiYi Zi , XдYдZд , XиYиZи и др., связанные с отдельно взятой поверхностью. Очевидно, например, что поверхности детали, обозначенные 1 (рис. 3.1.1), удобно описывать в системе координат X1Y1Z1 , поверхности 2 имеют более простое аналитическое представление в системе

координат X2Y2 Z2 , а поверхности 3 – в системе координат XдYдZд . Аналитическое описание детали будет

получено, если уравнения всех ее поверхностей будут представлены в некоторой общей системе координат, например, в системе координат XдYдZд . Для этого начала систем координат X1Y1Z1 и X2Y2 Z2 следует

совместить с началом системы координат XдYдZд и обеспечить однонаправленность соответствующих осей координат. Например, чтобы систему координат X1Y1Z1 совместить с системой координат XдYдZд , следует:

- первую систему координат X1Y1Z1 развернуть вокруг оси X1 в отрицательном направлении на угол

системы координат. После двух поворотов оси систем координат становятся однонаправленными;

-из последнего положения первую систему координат сместить вдоль оси Z1 на величину a , равную расстоянию между плоскостями координат X1Y1 и XдYд . Такое преобразование описывается оператором Tr a, Z1 переноса системы координат;

-и, наконец, из последнего положения сместить первую систему координат вдоль оси X1 на величину

b , равную расстоянию между плоскостями координат Y1Z1 и YдZд . Это преобразование описывается оператором Tr b, X1 переноса системы координат.

Рис. 3.1. Системы координат детали.

Результирующий переход от системы координат X1Y1Z1 к системе координат XдYдZд описывается оператором результирующего преобразования координат Rs 1 д , который определяется совокупностью и

последовательностью применения операторов Rt 90 , X1 , Rt 90 , Z1 , Tr a, Z1 и Tr b, Z1 частных

преобразований координат.

Аналогичное справедливо и в отношение детали (рис. 3.1.2): в этом случае поворот первой системы координат X1Y1Z1 вокруг оси Y1 на угол описывается оператором Rt , Y1 поворота системы координат.

При автоматизированном воспроизведении сложных поверхностей, состоящих из отдельных отсеков, на станке ЧПУ требуется определить положение каждого из формообразуемых отсеков поверхности детали. Отдельные отсеки сложной поверхности Д детали, как и отдельные поверхности одной и той же детали, могут быть аналитически представлены в различных (своих) системах координат. Вследствие преимуществ такого подхода к заданию и аналитическому описанию отсеков отдельных поверхностей, он часто используется при решении задач формообразования поверхностей деталей. Это выполняется в порядке, рассмотренном выше.

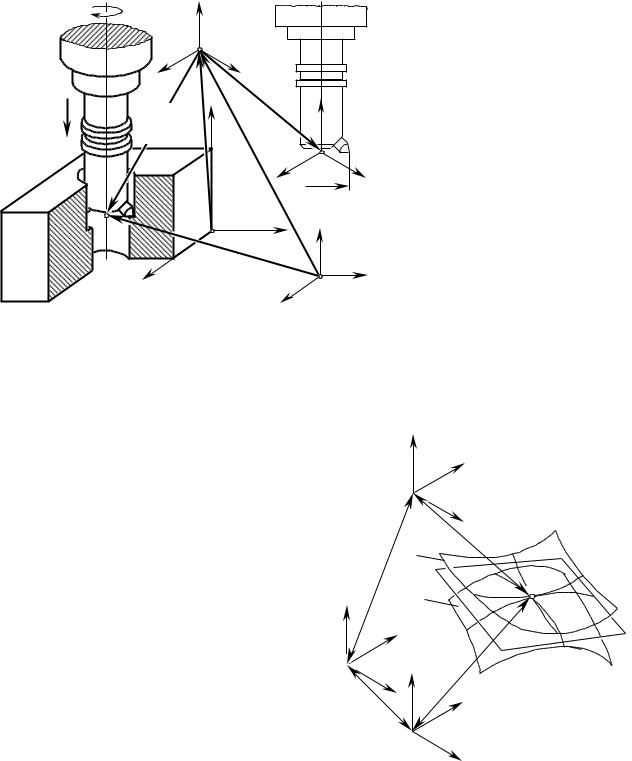
Автоматизированная подготовка управляющих программ для многокоординатных металлорежущих станков с ЧПУ предусматривает формирование в памяти системы ЧПУ численных данных, описывающих обрабатываемую деталь, инструмент, движения рабочих органов станка и др. в некоторой системе координат. При подготовке к обработке даже относительно простой детали (рис. 3.2) должны быть установлены размерные связи между системой координат XстУстZст станка с ЧПУ, относительно которой производится

отсчет размеров, исходной точкой, являющейся началом программы обработки (она служит началом системы координат Xи.т.Yи.т.Zи.т.), деталью и инструментом, с которыми связаны системы координат XдУдZд и

XиУиZи соответственно и др. При этом многие отдельные поверхности обрабатываемой детали (плоскости,

наружные и внутренние круглые цилиндры, внутренние и наружные участки поверхностей тора, конуса, сферы, винтовых поверхностей и др.) обычно задаются в своих системах координат. Кроме перечисленных (см. рис. 3.2) используются и иные (вспомогательные, промежуточные и пр.) системы координат, необходимые для упрощения аналитического описания процесса обработки заданной детали.

Взаимное расположение и относительная ориентация систем координат определяется векторами rи , rи.т., r прогр., r п , ri и др., для оперирования которыми необходимо иметь их аналитическое представление в

некоторой общей для всех векторов и других геометрических элементов процесса формообразования системе координат. Приведение перечисленных векторов к общей системе координат предполагает наличие соотношений, описывающих связи между используемыми системами координат.

удобно (хотя это и не является обязательным) представлять в матричной форме. В этом случае для нахождения опреатора Rs 2 1 результирующего преобразования координат операции с ними существенно

упрощаются.

Рассмотрим основные свойства матриц и операций с ними, которые находят применение при решении задач формообразования поверхностей деталей.

3.2.Сведения о матрицах, необходимые для решения задач формообразования поверхностей деталей

Решение задач формообразования поверхностей деталей требует многократных прямых и обратных преобразований систем координат и пространства, в которых одни величины линейно выражаются через другие. Операции такого рода удобно описывать при помощи матриц.

3.2.1. Основные определения. Матрицей принято называть совокупность элементов aij ( i 1, 2, , m ; j 1, 2, , n ), расположенных в виде прямоугольной таблицы из “m ” строк и “n ” столбцов, где m и n – числа, определяющие размер матрицы:

К прямоугольным матрицам относится матрица-столбец, часто называемая вектором (у нее n 1 ):

Если m n , матрица будет квадратной, в этом случае n – порядок матрицы.

Линия, на которой располагаются элементы aij квадратной матрицы, является главной диагональю, а

элементы aii ( i 1, 2, , n ) – главными.

Линии, параллельные главной диагонали, называют кодиагоналями. Квадратная матрица будет симметричной, если aij a ji .

Диагональная матрица, все элементы которой равны единице, является единичной и обозначается E :

0 0 1

В алгебре матриц единичная матрица имеет такое же значение, какое в элементарной алгебре – единица. Матрица, все элементы которой равны нулю, является нулевой и обозначается символом 0 .

Две матрицы одинаковых размеров равны, если равны их соответствующие элементы.

Кодиагональная (или ленточная) матрица – это квадратная матрица с ненулевой диагональю, по обе стороны от которой имеется одинаковое число ненулевых диагоналей; остальные элементы кодиагональной матрицы равны нулю. Примером трехдиагональной матрицы служит матрица:

Применение кодиагональных матриц позволяет более эффективно использовать память ЭВМ и других вычислительных устройств. Поэтому целесообразно предварительно матрицы преобразовывать таким образом, чтобы возможно большее их количество представляло собой кодиагональные матрицы.

В пределах каждой симметричной пары диагоналей все элементы кодиагональной матрицы могут быть равны один другому. В этом случае матрица становится модулированной кодиагональной матрицей вида

Квадратная матрица, у которой все элементы, расположенные по одну сторону от главной диагонали,

Симметричная квадратная матрица тождественна своей транспонированной матрице, т.е. в этом случае справедливо тождество A A Т .

В свою очередь матрицы могут быть элементами другой матрицы. Матрица, составленная из других матриц, известна как клеточная или квазиматрица:

Если в квазиматрице все элементы, кроме диагональных, равны нулю, она преобразуется в

Кодиагональная и треугольная матрицы в этом случае будут квазидиагональной и квазитреугольной соответственно.

3.2.2. Операции с матрицами. Математические операции с матрицами сводятся к операциям с их элементами. Матрицы можно складывать, умножать на скаляр, умножать на вектор (представленный в виде матрицы-столбца), а также умножать одну матрицу на другую. Делить матрицы одна на другую нельзя.

Складывать одну матрицу с другой можно только если их размеры одинаковы. В этом случае суммой

Сложение матриц обладает свойством коммутативности (от перестановки матриц их сумма не меняется) и подчиняется сочетательному закону:

A B B A ;

A B С A B С .

Умножение матрицы на скаляр p равносильно умножению всех ее элементов на это число: bij p aij ;

Действие вычитания в алгебре матриц определяется как сложение двух матриц, одна из которых умножена на скаляр p 1 .

При умножении двух матриц каждый элемент матрицы произведения С равен сумме произведений элементов k ой строки матрицы A на соответствующие элементы j го столбца матрицы B

n

(3.1) сik ai1b1k ai2b2k ... ainbnk aijb jk . j 1

Из этого следует, что две матрицы могут быть перемножены лишь в случае, когда число столбцов первой (левой) равно числу строк второй (правой). Если размер первой матрицы m n , а второй n p , то матрица

произведения С будет иметь размер m p . В общем случае A B B А (если существуют оба

произведения), т.е. операция умножения матриц не обладает свойством коммутативности. Поэтому следует оговаривать порядок перемножения матриц (например, умножим матрицу B слева на матрицу A ).

Аналогично перемножаются прямоугольные матрицы с согласованным числом строк и столбцов:

Умножение матрицы на вектор является частным случаем перемножения прямоугольных матриц. Умножение производится в порядке, определяемом уравнением (1). В этом случае векторы записываются в виде матрицы-столбца:

Вектор X перепишем в виде столбцовой матрицы

19

Х 12 19 12 4 Т .

4

Тогда

Полученную матрицу-столбец снова можно записать в векторной форме: С 75i 138j 192k .

Произведение матриц подчиняется сочетательному и распределительному законам:

A B С A B С A B С ;

С A B С A С B ;

A B С A С B С ,

но

A B С С A B .

Втеории формообразования поверхностей деталей обычно приходится выполнять операции с квадратными матрицами. С квадратной матрицей связано понятие определителя и обратной матрицы.

Определитель матрицы составляется из ее элементов при неизменном их расположении и называется

модулем матрицы:

Между матрицей и определителем существует принципиальное различие. Запись определителя в виде упорядоченной таблицы только внешне напоминает квадратную матрицу. Определитель – это число, а запись его в виде таблицы – только удобная форма, позволяющая по известным правилам вычислять его значения.

Для квадратной матрицы A обратной матрицей будет квадратная матрица A 1 того же порядка, обладающая свойством:

A A 1 A 1 A Е ,

где Е – единичная матрица того же порядка. Решение матричного уравнения

можно получить, умножив обе части этого равенства на матрицу A 1 : A 1 A Х A 1 D , но посколькуA 1 A E , следовательно, Х A 1 D .

Таким образом решение матричного уравнения (2) сводится к нахождению обратной матрицы A 1 .

Для заданной матрицы A обратная матрица A 1 существует лишь в случае, когда исходная матрица не является особенной, т.е. определитель матрицы не равен нулю: Det A 0 .

Известно много методов нахождения матрицы, обратной заданной. Остановимся на двух из них. Обратную матрицу можно получить путем деления всех элементов присоединенной (союзной) матрицы на

определитель исходной матрицы. Присоединенная матрица получается путем транспонирования матрицы, составленной из алгебраических дополнений элементов исходной матрицы.

Элементы обратной матрицы равны

Применение рассмотренного способа нахождения обратной матрицы оправдано в случаях, когда исходная матрица имеет порядок не выше четвертого. Это ограничение вызвано тем, что при более высоком порядке исходной матрицы объем вычислительной работы резко увеличивается.

Другой способ нахождения обратной матрицы заключается в последовательном вычислении обратной матрицы путем подбора при помощи единичной матрицы. Записав рядом с заданной матрицей единичную матрицу, производим сложение строк, предварительно подобрав множители так, чтобы на месте заданной матрицы получить единичную. В этом случае на месте единичной матрицы будет искомая обратная матрица.

Пример 3.4. Вычислить матрицу, обратную матрице четвертого порядка

Ко второй, третьей и четвертой строкам обеих матриц прибавим их первую строку, умноженную: на 1 – для второй строки, на 1 – 2

для второй строки и на 1 – для четвертой строки.

2

Первая строка каждой матрицы остается неизменной. Получим

Теперь к первой, третьей и четвертой строкам полученных матриц прибавим их вторую строку, умноженную: на 6 – для первой строки, на –4 – для третьей строки и на –1 – для четвертой строки. Имеем