
7 семестр / Основы_физич_химии_Теория_и_задачи_Еремин_и_др_2005_480с
.pdf
134 Г л а в а 2. Приложения химической термодинамики
Если x″ = x′, то ∂p = 0, таким образом, приходим к формули-∂x′ T
ровке второго закона Коновалова:
Точки максимума и минимума на кривой общего давления пара отвечают раствору, состав которого одинаков с составом равновесного с ним пара.
Растворы, у которых составы пара и жидкости совпадают, называ-
ются азеотропами (см. рис. 8.4).
Из обобщенного уравнения Ван-дер-Ваальса следует и третий за-
кон Коновалова:
В изотермических (или изобарических) условиях составы рас-
dx′
твора и пара изменяются симбатно, т.е. dx′′ > 0 .
p |
T |
|
|
l |
|
|
g |
|
g |
|
l |
x → |
x → |
p |
T |
|
|
l |
g |
|
|
|
l |
|
g |
x → |
x → |
Рис. 8.4 |
T–x и p–x диаграммы бинарных систем с верхним и нижним азеотропом, |
|
g – паровая фаза, l – жидкость |
|

Г л а в а 2. Приложения химической термодинамики |
135 |
Законы Коновалова получены эмпирически, но они также могут быть выведены как следствия обобщенного уравнения фазовых равновесий Ван-дер-Ваальса.
Равновесие конденсированных фаз. Уравнения Планка – Ван Лаара и Шредера
Предположим, что чистый компонент В (фаза ′) находится в равновесии с насыщенным раствором (″). Рассмотрим случаи постоянства (а) давления, (б) температуры.
а) p = const
В этом случае
•dp = 0,
• x′ = 1, dx′ = 0, |
S ′ |
= S o |
, |
|
B |
B,тв |
|
• |
растворимость компонента B равна мольной доле В в растворе (x″), |
|||
• |
в идеальном растворе |
|
→ H o |
при x → 1. 1 |
H ′′ |
||||
|
|
B |
B,ж |
|
С учетом принятых допущений уравнение Ван-дер-Ваальса упрощается
|
|
|
|
|
|
|
|
|
|
o |
|
|
|
|
|
′′ |
|
|
|
|
RT |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
∂µ B |
|
|
|
|
|
|
|||||||
0 − (SB′ − SB′′ )dT = (SB′′ − SB,тв )dT = |
|
|
|
|
|
|
dx′′ = |
|
dx′′ = RTdlnx′′ |
||||||||||||||||
∂x′′ |
|
|
x′′ |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B p,T |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
− |
S o |
|
|
|
− H o |
|
|
|
|
|
|
|||||
|
|
|
|
∂ ln x |
|
|
S ′′ |
|
H ′′ |
|
|
|
∆ плH B |
|
|||||||||||
|
|
|
= |
|
B |
B,тв |
= |
|
B |
|
|
|
|
B,тв |
= |
, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
RT |
|
|
|
RT 2 |
|
RT 2 |
|
|||||||||||||
|
|
|
|
∂T p |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
∂ln x |
|
|
= |
∆ |
плH B |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
∂T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
RT |
2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
p,насыщ |
|
|
|
|
|
|
|
|
|
|||||||
получило название уравнение Шредера. Оно описывает изменение растворимости твердого вещества с изменением температуры.
Интегрируя уравнение Шредера в предположении независимости энтальпии от температуры, получаем уравнение, описывающее кривую кристаллизации компонента В:
ln x = ∆ плH B (T − Tпл ) . RTплT
1 |
|
– H o |
= |
|
− H o |
+ H o |
− H o |
= |
H ex |
|
|
|
|
, где ∆плHB – |
H ′′ |
H ′′ |
+ ∆ |
пл |
H |
B |
|||||||||
|
B |
B,тв |
|
B |
B,ж |
B,ж |
B,тв |
|
B |
|
|
|
теплота плавления переохлажденной жидкости, а H Bex → 0 при xВ → 1.
(8.11.а)
(8.11.б)

136 |
|
Г л а в а 2. Приложения химической термодинамики |
||||
T |
|
|
|
|
|
Аналогичное уравнение можно |
|
|
|
|
|
записать и для другого компонента |
|
|
|
|
|
|
раствора. Две кривые кристаллиза- |
|
|
|
l |
|
|
ции |
пересекаются в эвтектической |
|
|
|
|
|
точке (см. рис. 8.5) |
|
|
|
|
l + B |
|
|
Выводы из уравнения Шредера: |
A + l |
|
|
|
• |
так как ∆плH > 0, то раствори- |
|
|
|
|
|
|||
|
|
|
|
|
мость твердых веществ в жидкости |
|
|
|
|
|
|
увеличиваетсясростомтемпературы, |
|
|
|
A + B |
|
|
• вещества с более высокой тем- |
|
А |
|
x→ |
|
В |
пературой плавления менее раство- |
|
|
|
римы, |
||||
Рис. 8.5 |
|
T–x-диаграмма бинарной |
|
• растворимость вещества во всех |
||
системы с простой эвтектикой |
растворителях, с которыми оно об- |
|||||
|
|
|
|
|
разует идеальный раствор, не зави- |
|
|
|
|
|
|
сит от природы растворителя. |
|
|
|
б) T = const |
|
|
|
|
|
|
Преобразуяобобщенное уравнениеВан-дер-Ваальсасучетомтого, что |
||||
|
• |
dT = 0, |
= V o |
|
|
|
|
• |
x′ = 1, dx′ = 0, V ′ |
, |
|
|
|
|
|
B |
B,тв |
|
|
|
|
• x″ – растворимость второго компонента, |
|||||
|
получаем уравнение Планка–Ван Лаара |
|||||
(8.12) |
|
∂ ln x |
= − |
∆ плVB |
, |
|
∂p T ,насыщ |
|
|||
RT |
где ∆плVB – изменение объема компонента В при неравновесном плав-
лении (ниже Tпл).
Уравнение Планка–Ван Лаара описывает влияние давления на растворимость твердого вещества. Согласно уравнению (8.12), с повышением давления должна уменьшаться растворимость веществ, у которых мольный объем жидкости больше мольного объема твердой фазы.
С помощью уравнений (8.5–8.6) можно также получить все выражения, описывающие коллигативные свойства растворов (см.§ 6). Основная проблема, связанная с использованием дифференциальных уравнений фазовых равновесий (в том числе, обобщенного уравнения Ван- дер-Ваальса) – получение их интегральной формы.
ПРИМЕРЫ
Пример 8-1. Получите аналитическое выражение, описывающее кривую ликвидус в бинарной системе с неограниченной растворимостью компонентов в твердом и жидком состоянии. Растворы можно считать идеальными.
Г л а в а 2. Приложения химической термодинамики |
137 |
Решение. Условия равновесия жидкой и твердой фаз описываются уравнениями (8.4.а):
|
o |
− x |
s |
|
o |
|
− x |
l |
), |
|
µ A ,s + RTln(1 |
|
) = µ A ,l + RTln(1 |
|
|||||||
|
o |
s |
|
|
o |
l |
|
|
|
|
|
|
|
. |
|
|
|
||||
µ B,s + RT ln x |
|
= µ A ,l + RT ln x |
|
|
|
|||||
Учитывая, чторазности
µo |
− µo |
= ∆ |
G (T ), |
µo |
− µo |
= ∆ |
G (T ) |
A,l |
A,s |
|
пл A |
B,l |
B,s |
|
пл B |
представляют собой мольные энергии Гиббса плавления компонентов (параметры стабильности), записанную выше систему уравнений можно переписать в виде
|
1 − xl |
= −∆ плGA (T ) / RT , |
||
ln |
|
|
||
1 − xs |
||||
|
|
|||
|
xl |
|
|
|
|
= −∆ плGB (T ) / RT. |
|||
ln |
|
|||
xs |
||||
|
|
|
||
Выражаем из второго уравнения xs и подставляем в первое. После перегруппировки слагаемых получаем уравнение кривой ликвидус:
|
|
|
|
|
∆ плGA (T ) |
|
|
||||||
|
|
|
|
1 − exp |
|
|
|
|
|
|
|
||
|
|
|
|
|
RT |
|
|
|
|
||||
x |
l |
= |
|
|
|
|
|
|
|
. |
|||
|
|
∆ плGB (T ) |
− exp |
|
∆ плGA (T ) |
||||||||
|
|
|
|
||||||||||
|
|
|
exp |
|
|
|
|
|
|
|
|
||
|
|
|
RT |
|
|
RT |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||
Пример 8-2. Рассчитайте кривую ликвидус соединения AB. Примите, что жидкость можно считать идеальным раствором. Энергия Гиббса образования фазы АВ из жидких компонентов описывается уравнением
∆fGo(T) = ∆fHo – T∆fSo.
Решение. Если в системе образуется соединение, не имеющее области гомогенности, то использовать условие равновесия в виде равенства химических потенциалов нельзя, так как для фазы постоянного состава понятие химического потенциала не определено. В этом случае система уравнений (8.4.а) может быть сведена к уравнению
(1 − xs )µ A ,l + xsµ B,l = Gs ,
где xs – состав соединения, в рассматриваемом случае xs = 0.5. Подставляя в это уравнение выражения (8.4.б) для химических по-
тенциалов компонентов расплава и учитывая, что избыточные функции равны 0, получаем
(1 − xs )(µ oA ,l + RT ln(1 − xl ))+ xs (µ oB,l + RT ln xl )= Gs .

138 Г л а в а 2. Приложения химической термодинамики
Разность
Gs − (1 − xs )µ oA ,l − xsµ oB,l = ∆ f G o
представляет собой стандартную энергию Гиббса образования фазы АВ из жидких компонентов. С учетом этого последнее равенство можно переписать в виде:
(1 − xs )RT ln(1 − xl ) + xs RT ln xl = ∆ f G o = ∆ f H o − T ∆ f S o .
Выражаем в явном виде температуру:
T = |
|
|
|
∆ f H o |
|
|
. |
∆ |
f |
S o + R (1 − xs ) ln(1 |
− xl ) + xs ln xl |
||||
|
|
|
|
|
|
||
Для рассматриваемой системы |
|
|
|
||||
|
|
T = |
∆ f H o |
|
. |
||
|
|
∆ f S o + 0.5R ln (xl (1 − xl )) |
|||||
Пример 8-3. Рассчитайте растворимость висмута в кадмии при 150 и 200 °C. Энтальпия плавления висмута при температуре плавления (273 °C) равна 10.5 кДж моль–1. Примите, что образуется идеальный раствор и энтальпия плавления не зависит от температуры.
Решение. Воспользуемся формулой
ln x = |
∆ плH |
1 |
|
− |
1 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
. |
|
|||||||
R |
|
|
|
|
|
T |
|
|||||||||
|
|
|
|
|
Tпл |
|
|
|
|
|
|
|||||
При 150 °C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln x = |
10500 |
|
1 |
|
− |
|
1 |
|
|
|
, |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
8.314 |
546 |
|
423 |
|||||||||||||
|
|
|
|
|
|
|
||||||||||
откуда x = 0.510. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При 200 °C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln x = |
10500 |
|
1 |
|
− |
|
1 |
|
|
|
, |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
8.314 |
546 |
|
473 |
|||||||||||||
|
|
|
|
|
|
|
||||||||||
откуда x = 0.700.
Растворимость увеличивается с температурой, что характерно для эндотермического процесса.
Ответ. x = 0.510 при 150 °C и x = 0.700 при 200 °C.

Г л а в а 2. Приложения химической термодинамики |
139 |
ЗАДАЧИ
8-1. Физические методы глубокой очистки путем многократного повторения процессов плавления-кристаллизации основаны на неравномерном распределении вещества при фазовых переходах. Покажите, что при любой температуре, отличной от Tпл,В, коэффициент распре-
xl
деления k = B отличен от 1. Примите, что растворы можно считать
xBs
идеальными.
8-2. Постройте T–x диаграмму и определите координаты эвтектической точки в системе бензол–хлорбензол, если в твердом состоянии эти вещества нерастворимы, а в жидком образуют идеальный раствор.
Tпл,C H |
6 |
= 278.7 K, |
∆плHC H |
6 |
= 9.83 кДж моль–1, |
6 |
|
6 |
|
||
Tпл,C H Cl = 228.2 K, |
∆плHC H Cl = 9.56 кДж моль–1. |
||||
6 |
5 |
|
6 |
5 |
|
8-3. Постройте T–x диаграмму и рассчитайте координаты эвтектической точки в системе пара-нитробензол – пара-нитроанилин, если в твердом состоянии эти вещества взаимно нерастворимы, а в жидком образуют идеальный раствор. Температуры плавления пара-нитробензола и пара- нитроанилина равны 446.0 и 420.7 К соответственно. Энтальпии плавления 26.2 и 21.5 кДж моль–1.
8-4. Определите координаты эвтектической точки в системе Al–Si, если известно, что компоненты взаимно нерастворимы в твердом состоянии и образуют идеальный расплав.
Tпл,Al = 660 °C, |
∆плHAl = 6.4 кДж моль–1, |
Tпл,Si = 1420 °C, |
∆плHSi = 31.2 кДж моль–1. |
8-5. Рассчитайте T–x диаграмму системы K–Rb, компоненты которой неограниченно растворимы в твердом и жидком состоянии.
Tпл,K = 336 К, |
∆плHK = 558 кал моль–1, |
Tпл,Rb = 312 К, |
∆плHRb = 524 кал моль–1. |
8-6. Рассчитайте T–x диаграмму системы Na2SO4–Ag2SO4, если известно, что компоненты неограниченно растворимы в твердом и жидком состоянии.
Tпл,Na SO |
|
= 924 K, |
∆плHNa SO |
4 |
= 56.5 кДж моль–1, |
|||
2 |
4 |
|
2 |
|
|
|
||
Tпл,Ag |
SO |
4 |
= 1157 K, |
∆пл HAg |
SO |
|
= 49.6 кДж моль–1. |
|
2 |
|
|
2 |
|
4 |
|
||
8-7. Рассчитайте и сравните с литературными данными T–x диаграмму системы Se–Te, компоненты которой неограниченно растворимы в твердом и жидком состояниях.
Tпл,Se = 494 К, |
∆плHSe= 1600 кал моль–1, |
Tпл,Te = 722 К, |
∆плHTe = 4180 кал моль–1. |
140 |
Г л а в а 2. Приложения химической термодинамики |
8-8. Рассчитайте идеальную растворимость антрацена в бензоле при 25 °C в единицах моляльности. Энтальпия плавления антрацена при температуре плавления (217 °C) равна 28.8 кДж моль–1.
8-9. Рассчитайте растворимость п-дибромбензола в бензоле при 20 и 40 °C, считая, что образуется идеальный раствор. Энтальпия плавления п-дибромбензола при температуре его плавления (86.9 °C) равна 13.22 кДж моль–1.
8-10. Рассчитайте растворимость нафталина в бензоле при 25 °C, считая, что образуется идеальный раствор. Энтальпия плавления нафталина при температуре его плавления (80.0 °C) равна 19.29 кДж моль–1.
8-11. Рассчитайте растворимость антрацена в толуоле при 25 °C, считая, что образуется идеальный раствор. Энтальпия плавления антрацена при температуре плавления (217 °C) равна 28.8 кДж моль–1.
8-12. Рассчитайте температуру, при которой чистый кадмий находится в равновесии с раствором Cd – Bi, мольная доля Cd в котором равна 0.846. Энтальпия плавления кадмия при температуре плавления
(321.1 °C) равна 6.23 кДж моль–1.
8-13. Оцените растворимость серы в бензоле при 50 °С, если известно, что:
∆плHмон = 1.26 кДж моль–1 при 119 °С,
∆Hромб→мон = 0.36 кДж моль–1 при 95.5 °С; разность мольных теплоемкостей:
∆Сp,мон/ромб = −0.98 + 3.01 10–3T, ∆Сp,жидк/ мон = –0.67 – 6.11 10–3T.
В растворе сера находится в виде S8.
8-14. Покажите, что в бинарной системе, компоненты которой образуют идеальный жидкий раствор, невозможно существование азеотропа.
8-15. Покажите, при каких отклонениях от идеальности (положительных или отрицательных) возможно расслаивание регулярного раствора. Объясните, почему купол расслаивания (кривая взаимной растворимости) в этом случае симметричен относительно x = 0.5.
8-16. Рассчитайте, при каком значении энтальпии смешения регулярного раствора критическая температура расслаивания равна:
а) 300 К; б) 400 К.
8-17. Определите состав и температуру кипения азеотропа, если компоненты А и В образуют регулярный раствор, параметр взаимодействия равен g0. Давления паров чистых компонентов в интервале температур T1 ÷ T2 описываются уравнениями:
ln pA = aA – bA/T, |
ln pB = aB – bB/T. |

Г л а в а 2. Приложения химической термодинамики |
141 |
8-18. Бензол и циклогексан образуют регулярный раствор с параметром взаимодействия 2000 Дж моль–1. Определите состав и температуру кипения образующегося азеотропа, если давления паров бензола и циклогексана описываются уравнениями Антуана:
ln pС6H6(Торр) = 15.90 – 2789/(T – 52.4), ln pС6H12(Торр) = 15.75 – 2766/(T – 50.5).
8-19. Рассчитайте состав азеотропа, образующегося в системе А–В, если параметр взаимодействия регулярного раствора равен 3600 Дж моль–1, а давления насыщенных паров компонентов
ln pА(Торр) = 21.64 – 5232/T, ln pВ(Торр) = 17.12 – 3705/T.
8-20. На рисунке изображены концентрационные зависимости энергий Гиббса двух растворов при различных температурах. Что можно сказать об устойчивости этих растворов в указанном интервале температур?
A |
T1 |
B |
|
l1 |
|
G |
|
G |
|
|
l2 |
A |
T2 |
B |
|
|
l1 |
|
l2 |
|
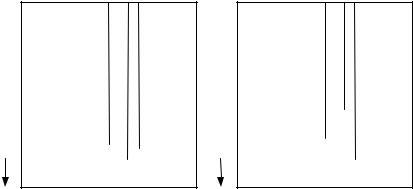
8-21. На рисунке изображена концентрационная зависимость энергии Гиббса некоторого раствора при температуре T. Охарактеризуйте фазовое состояние системы при составах x1, x2, x3.
A |
x1 |
x2 |
x3 |
B |
G |
|
|
|
|
142 |
Г л а в а 2. Приложения химической термодинамики |
8-22. На рисунке представлены энергии Гиббса трех соединений AB, A2B3, AB2 при двух температурах T1 и T2. Определите, при какой температуре фаза A2B3 будет неустойчива по отношению к соседним фазам. Обоснуйте ваш выбор.
A |
T1 AB AB2 B |
A |
|
AB AB2 |
B |
T2 |
G |
G |
8-23. Концентрационная зависимость ∆fG°(x, T = const), x = 0 ÷ 1, некоторой фазы описывается полиномом
∆fG° = a + blnx + cx2, a, b > 0.
Какие ограничения накладываются на величину c, если данная фаза устойчива во всей области составов?
8-24. Концентрационная зависимость ∆fG°(x, T = const), x = 0.2 ÷ 0.7, некоторой фазы описывается полиномом
∆fG° (кДж моль−1) = −10.0 + 8.2x2 + 7.2x3.
Будет ли данная фаза устойчива в указанной области составов?
8-25. Иногда при оценках термодинамических свойств соединений их стандартные энтальпии и энтропии образования рассчитывают как средние значения между соответствующими свойствами двух соседних соединений. Покажите, что при таком способе расчета соединение AB2 будет находиться в состоянии безразличного равновесия относительно
AB и AB3.
8-26. Может ли фаза вещества существовать за пределами области ее термодинамической устойчивости? Если – «нет», то почему, если «да» – то при каких условиях?
8-27. С помощью приведенной на рисунке фазовой диаграммы системы Li–Si определите, что будет представлять собой сплав 1 г Li и 1.714 г Si:
а) медленно охлажденный от 700 K до комнатной температуры; б) закаленный от 700 K.

Г л а в а 2. Приложения химической термодинамики |
143 |
|||||||||
1800 |
|
|
|
|
|
|
|
|
|
|
1600 |
|
|
3 |
|
|
|
l |
|
|
|
|
|
|
Si |
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
1400 |
|
4 |
Li |
7 |
|
|
|
|
|
|
|
|
Si |
|
Si |
|
|
|
|
|
|
|
5 |
13 |
|
12 |
|
|
|
|
|
|
1200 |
Si |
Li |
|
Li |
|
|
|
|
|
|
|
22 |
|
|
|
|
|
|
|
|
|
|
Li |
|
|
|
|
|
|
|
|
|
1000 |
|
|
|
|
|
|
|
|
|
|
800 |
|
|
|
|
|
|
|
|
|
|
600 |
|
|
|
|
|
|
|
|
|
|
400 |
|
|
|
|
|
|
|
|
|
|
0.0 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1.0 |
Li |
|
|
|
|
x |
|
|
|
|
Si |
8-28. Для системы Li–Si изобразите схематично температурные зависи- |
||||||||||
мости энергий Гиббса твердых фаз в интервале 500 800 К. |
|
|
||||||||
8-29. С помощью приведенной на рисунке фазовой диаграммы системы |
||||||||||
Zr–B определите, что будет представлять собой сплав с содержанием |
||||||||||
8 мол. % Zr: |
|
|
|
|
|
|
|
|
|
|
а) медленно охлажденный от 1800 К до комнатной температуры; |
||||||||||
б) закаленный от 1800 К. |
|
|
|
|
|
|
|
|||
3400 |
|
|
|
|
|
|
|
|
|
|
3200 |
|
|
|
|
|
|
|
|
12 |
|
3000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ZrB |
|
|
2800 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2600 |
|
|
|
|
|
|
|
|
|
|
2400 |
|
|
|
|
|
|
|
|
|
|
2200 |
|
|
|
|
|
|
|
|
|
|
2000 |
|
|
|
|
|
|
|
|
|
|
1800 |
|
|
|
|
|
|
|
|
|
|
1600 |
|
|
|
|
|
|
|
|
|
|
1400 |
|
|
|
|
|
|
|
|
|
|
1200 |
|
|
|
|
|
2 |
|
|
|
|
1000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ZrB |
|
|
|
|
|
800 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
600 |
|
|
|
|
|
|
|
|
|
|
0 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1.0 |
|
|
|
|
Мольная доля (Х) компонента B всистемеA - B |
||||||
8-30. Для системы Zr–B изобразите схематично температурные зависи- |
||||||||||
мости энергий Гиббса твердых фаз в интервале 600 1800 К. |
|
|
||||||||
