Добавил:

Sahsha Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Тульский Государственный Университет

Предмет:

Физическая химия

Файл:

7 семестр / Основы_физич_химии_Теория_и_задачи_Еремин_и_др_2005_480с

.pdf

Скачиваний:

Добавлен:

02.01.2023

Размер:

5.51 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 4812 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

114	Г л а в а 2. Приложения химической термодинамики

фаз s1, s2 произвольны при соблюдении условия n = ns1 + ns2. Таким образом, при температуре Ts1→s2 равновесно сосуществуют две твердые

фазы s1 и s2. Аналогичные рассуждения можно повторить для температуры Ts2→l, которая соответствует равновесию твердой s2 и жидкой фаз

	при давлении p1.
	(a)						(б)
G–H0				G–H0
			p1 = const				p2 = const
				(s1)				(s1)
				(s1)				(s2)
				(s2)				(s2)
				(l)				(l)
				(g)				(g)
T 1	T s1→s2	T s2→l	T l → g	T	T 1	T s1→s2	T тр.т. T	T

Рис. 7.2

Рис. 7.3

Температурные зависимости энергий Гиббса различных фаз однокомпонентной системы

На рис. 7.2.б приведены графики зависимости энергий Гиббса от температуры для всех четырех фаз при другом давлении (p2). Как видно из рисунка, при изменении давления от p1 до p2 изменяется температура, при которой равновесно сосуществуют две твердые фазы. При давлении p2 и температуре Tтр.т. пересекаются линии, описывающие температурные зависимости энергий Гиббса трех фаз; это означает, что одновременно равновесно сосуществуют три фазы s2, l и g. На фазовой

диаграмме это состояние изображается тройной точкой.

Повторяя

аналогичные

рассуждения для других дав-

лений и температур, можно

построить

фазовую

диаграм-

му однокомпонентной систе-

мы, фрагмент которой пред-

ставлен на рис. 7.3. Следует

обратить

внимание

на тот

факт, что для расчета фазовых

тр.т.

равновесий необходимо знать

зависимости

энергий Гиббса

Ts2→l

T l→g

каждой из фаз во всей облас-

Ts1→s2(p2) Ts1→s2(p1)

ти изменения переменных p и

Фрагмент фазовой диаграммы

T. Границы устойчивости той

однокомпонентной системы

или иной фазы как раз и оп-

ределяются в ходе таких расчетов.

Г л а в а 2. Приложения химической термодинамики

115

Преимуществом представленного способа решения задачи расчета равновесий является одновременное определение и условий равновесия, и условий стабильности фаз.

II. Расчет фазовых равновесий из частных условий равновесия

В силу постоянства состава в однокомпонентной системе химический потенциал компонента совпадает с мольной энергией Гиббса:

µ = Gn = Gm .

II-а: Использование условий равновесия в интегральной форме

При расчете фазовой диаграммы можно исходить из равенства мольных энергий Гиббса компонента в сосуществующих фазах ′ и ″:

Gm′(p,T) = Gm″(p,T),

H′m – T S′m = H″m – T S″m,

	H /	− H //		∆H //→/ ( p,T )
T =	m	m	=	m	.
	Sm/			∆Sm//→/ ( p,T )
		− Sm//

Так как в рассматриваемой системе могут существовать четыре различные фазы, то для расчета фазовой диаграммы необходимо решить шесть уравнений:

Gms1(p,T) = Gms2(p,T),	Gms2(p,T) = Gml(p,T),
Gms1(p,T) = Gml(p,T),	Gms2(p,T) = Gmg(p,T),
Gms1(p,T) = Gmg(p,T)	Gml(p,T) = Gmg(p,T)

Линии, изображающие эти решения, приведены на рис. 7.4.

(7.4)

(7.5.а) (7.5.б)

(7.6)

(7.7)

p	(а)
p	p
	T

(б)

Фазовая диаграмма однокомпонентной системы:	Рис. 7.4
(а) – результаты расчета равновесий (7.7), (б) – устойчивые равновесия

116	Г л а в а 2. Приложения химической термодинамики

(7.8.а)

(7.8.б)

(7.9)

(7.10.а)

(7.10.б)

Чтобы от набора линий, изображающих равновесие фаз во всей области существования переменных, перейти к равновесной диаграмме состояний, надо отделить стабильные равновесия от метастабильных. Как видно из рисунка, уже в случае четырех фаз это вызывает некоторые затруднения, а при увеличении числа фаз или компонентности системы задача становится практически неразрешимой. В такой ситуации для построения фазовой диаграммы удобнее использовать условие минимума энергии Гиббса системы.

II-б: Использование условий равновесия в дифференциальной форме

В каждой точке кривой фазового равновесия выполняется условие:

dGm′ = dGm″

или

−S ′	dT + V ′ dp = −S ′′ dT + V ′′ dp .
m	m	m	m

Из последнего равенства получаем уравнение Клапейрона

dp		S ′′	− S ′		∆ ф.п. H m
	=	m	m	=			,
dT	=	V ′′	− V ′	=	T ∆	V	,
dT		V ′′	− V ′		T ∆	V
		m	m			ф.п. m

где ∆ф.п.Hm – мольная энтальпия равновесного фазового перехода (плав-

ления ∆плHm, испарения ∆испHm, возгонки ∆сублHm, перехода между кристаллическими модификациями), ∆ф.п.Vm – разность мольных объемов

фаз, находящихся в равновесии.

Для процессов испарения и возгонки уравнение (7.9) можно преобразовать, считая, что мольным объемом конденсированной фазы (жидкости или твердого тела) Vконд можно пренебречь по сравнению с мольным объемом пара Vпар, а пар подчиняется уравнению состояния идеального газа. Подставляя

(Vпар – Vконд) ≈ Vпар = RT/p,

получаем уравнение Клаузиуса–Клапейрона:

∆ сублH m

p∆ сублH m

∆

исп

m =

p∆

исп

TVпар

RT 2

TVпар

RT 2

или после разделения переменных:

d ln p =

∆ сублH m

d ln p =

∆

исп

T 2

Интегрирование последних уравнений в предположении, что ∆ф.п.Hm не зависит от температуры (что справедливо в узком интервале температур), дает:

Г л а в а 2. Приложения химической термодинамики

117

p = −

∆ ф.п.H m

+ C ,

(7.11.а)

∆ ф.п.H m

−

(7.11.б)

где C – константа интегрирования.

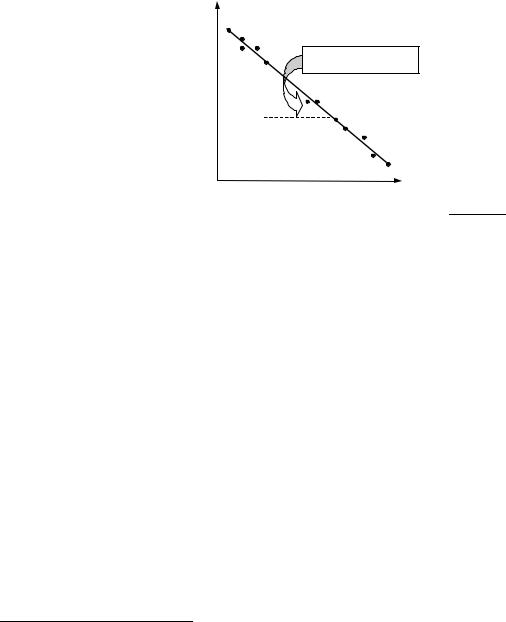
Зависимость ln p от 1/Т линейна, а наклон

прямой равен –∆ф.пHm/R

(см. рис. 7.5).

По уравнениям (7.11) можно рассчитать энтальпию испарения или возгонки, исходя из значений давления пара при нескольких (минимум – двух) температурах.

Мольные энтальпии возгонки, плавления и испарения при фиксированной температуре связаны соотношением:

lnp

tg α = –∆ф.п.Hm/R

1/T

Определение энтальпии испарения или возгонки (точками обозначены экспериментальные данные)

∆сублH = ∆плH + ∆испH.

Рис. 7.5

(7.12)

Энтальпию испарения жидкости можно приближенно оценить по правилу Трутона, согласно которому мольная энтропия испарения в нормальной точке кипения Tкип (при 1 атм) приблизительно постоянна:

	∆ испH		–1	–1
∆испS =		≈ 88 Дж моль		К .	(7.13)
∆испS =	Tкип	≈ 88 Дж моль		К .	(7.13)
	Tкип

Правило хорошо выполняется для неполярных жидкостей. Зависимость энтальпии фазового перехода от температуры можно

рассчитать, интегрируя выражение 1:

∂∆H

∂∆V

= ∆C

∆V − T

(7.14.а)

∂T

фаз.равн

фаз.равн.

При равновесии конденсированной фазы с идеальным газом второе слагаемое близко к нулю:

∂∆H	= ∆C p .	(7.14.б)
	= ∆C p .	(7.14.б)
∂T	фаз.равн

1 Вывод этой формулы см. в примере 7-2.

118	Г л а в а 2. Приложения химической термодинамики

(7.15.а)

(7.15.б)

(7.16)

(7.17.а)

(7.17.б)

Интегрирование последнего выражения приводит к

∆ ф.п. H (T2 ) = ∆ ф.п. H (T1 ) + ∫∆C p dT .

Для небольших интервалов температуры можно считать, что ∆Cp = const. В этом случае из уравнения (7.15.а) получаем:

∆ф.п.H(T) = ∆H0 + T ∆Cp,

где ∆Cp – разность теплоемкостей фаз, находящихся в равновесии, ∆H0 – константа, определяемая из известных значений ∆ф.пH и ∆Cp.

Подставляя уравнение (7.15.б) в уравнение (7.10.б) с последующим интегрированием, приходим к выражению:

ln p = − ∆RTH 0 + ∆CR p ln T + C ,

в котором С определяют из известных значений p, ∆H0 и ∆Cp. Описанные выше превращения «кристаллическая фаза (s1) → кри-

сталлическая фаза (s2)», «кристаллическая фаза → жидкость (l)», «кристаллическая фаза → пар (g)», «жидкость → пар» относятся к фазовым переходам первого рода, т.е., к переходам, при которых скачкообразно изменяются первые производные от химического потенциала,

Sm и Vm (рис. 7.6). При фазовых переходах второго рода первые про-

изводные от химического потенциала непрерывны, а претерпевают разрыв вторые производные: теплоемкость, коэффициент объемного расширения α и коэффициент изотермической сжимаемости β. К фазовым переходам второго рода относятся переходы, связанные с изменением симметрии кристаллической решетки, превращение ферромагнитных веществ в парамагнитное состояние, переход в сверхпроводящее состояние в отсутствие поля1. Связь между давлением и температурой для фазовых переходов второго рода дается уравнения-

ми Эренфеста:

dp		=		∆ ф.п.C p			,
dT				T		∆(αV )

				ф.п.
	dp		= −		∆(αV ) .
	dT
					∆(βV )

1 В магнитных полях переход из сверхпроводящего состояния в несверхпроводящее сопровождается скачкообразным изменением энтропии и объема, т.е. по принятой классификации относится к фазовым переходам первого рода.

Г л а в а 2. Приложения химической термодинамики

119

Gm I

	II
	T
Vm	I
	II
	T

Sm	I
	II
	T
Cp,m
	I

	Изменение термодинамических функций	Рис. 7.6
	при фазовых переходах первого и второго рода	Рис. 7.6

ПРИМЕРЫ

Пример 7-1. Определите число компонентов и число независимых реакций для системы, состоящей из O2, H2, NO, N2O4 и H2O(г).

Решение: число составляющих равно 5. Для определения числа компонентов и независимых реакций составляем формульную матрицу

O	O2	H 2 NO N 2 O4 H 2O								2 0		1	4	1
	O2	H 2 NO N 2 O4 H 2O								2 0		1	4	1
	2	0	1	4		1	,		[A] =	0	2	0	0	2
H	0	2	0	0		2	,		[A] =	0	2	0	0	2
H	0	2	0	0		2				0	0	1	2	0
N	0	0	1	2		0				0	0	1	2	0
N	0	0	1	2		0
и определяем ее ранг1. Определитель 3-го порядка
					2	0		1
					2	0		1
					0	2		0
					0	0		1

1 Напомним, что рангом матрицы называется наивысший порядок отличного от нуля определителя, рассчитанного среди набора всевозможных матриц, включающих исходную матрицу и матрицы, образованные из нее последовательным исключением строк и столбцов.

120	Г л а в а 2. Приложения химической термодинамики

отличен от нуля, следовательно, ранг матрицы равен 3. Компонентами не может служить набор O2, NO и N2O4, так как исключение из формульной матрицы 1-го и 3-го (1-го и 4-го или 3-го и 4-го столбцов) не изменяет ранга оставшейся матрицы. Поэтому в качестве компонентов можно взять, например, O2, H2, NO. Тогда независимыми реакциями будут 2 (2 = 5 – 3) реакции:

2 NO + O2 = N2O4	0.5 O2 + H2 = H2O,	(I)
2 NO + O2 = N2O4	H2 + 0.5 N2O4 = NO + H2O	(II)

или любые линейные комбинации реакций (I), (II).

Ответ. Число компонентов равно 3, число независимых реакций – 2.

Пример 7-2. Покажите, как рассчитать в общем случае температурную зависимость энтальпии фазового перехода вдоль кривой фазового равновесия (при изменении и p и T).

Решение: в общем случае

dH ( p,T ) = ∂H				dp + ∂H				dT
		∂p	T			∂T	p
Ранее было показано, что
	∂H				∂V	+ V .
		= −T				+ V .
	∂p T				∂T p

Для каждой из сосуществующих фаз можно записать:

	−T	∂V ′
dH ′( p,T ) =	−T				+ V ′ dp + С′ dT
			∂T			p
			∂T	p
	−T	∂V ′′
dH ′′( p,T ) =	−T				+ V ′′ dp + С′′ dT
			∂T			p
			∂T	p

Вычитая из второго равенства первое, получаем

	−T	∂∆V					dT .
d ∆H ( p,T ) =	−T				+ ∆V dp + ∆С	p	dT .
			∂T			p
			∂T	p

Разделив полученное уравнение на dT при условии движения вдоль фазовой кривой, приходим к выражению

∂∆H ( p,T )

∂∆V

∂p

= ∆С

dT +

∆V − T

∂T

фаз.равн.

∂T фаз.равн.

Г л а в а 2. Приложения химической термодинамики

121

С учетом уравнения Клапейрона это выражение преобразуется

∂∆H ( p,T )

∂∆V

∆H

= ∆С

dT +

∆V − T

∂T

T ∆V

фаз.равн.

∂T p

Пример 7-3. Рассчитайте изменение давления, необходимое для изменения температуры плавления льда на 1 °C. При 0 °C энтальпия

плавления льда равна 333.5 Дж г–1, удельные объемы жидкой воды и льда равны Vж. = 1.0002 см3 г–1 и Vтв. = 1.0908 см3 г–1.

Решение. Изменение объема при плавлении льда равно

Vж. – Vтв. = 1.0002 – 1.0908 = –0.0906 см3 г–1 = –9.06 10–8 м3 г–1.

dp		∆ плH		333.5		7		–1	–1
	=		=		= –1.348 10		(Па К		) = –133 атм К .
dT	=	T ∆Vпл	=	273.15 ( − 9.06 10−8 )	= –1.348 10		(Па К		) = –133 атм К .

Таким образом, при повышении давления на 133 атм температура плавления льда понижается на 1 градус. Знак «минус» показывает, что при повышении давления температура плавления понижается.

Ответ. ∆p = 133 атм.

Пример 7-4. Рассчитайте давление пара жидкого брома при 25 °C, если ∆fG° газообразного брома равна 3.110 кДж моль–1.

Решение. ∆испG° брома равно

∆fG° (Br2 (г)) = 3110 Дж моль–1.

	∆испG° = −RT ln	p	,
		po

откуда p = 0.2852	атм.
Ответ. p =	0.2852 атм.

Пример 7-5. Рассчитайте давление, при котором графит и алмаз находятся в равновесии при 25 °C. ∆fG° алмаза равно 2.900 кДж моль–1. Примите плотности графита и алмаза равными 2.25 и 3.51 г см–3, соответственно, и независящими от давления.

Решение. Изменение объема при переходе от графита к алмазу равно

∆V = 12	1	−	1	10–6	= –1.91 10–6 м3 моль–1.
	3.51		2.25

При начальном давлении p1 разность мольных энергий Гиббса ∆G1 = 2900 Дж моль–1, а при конечном давлении p2 разность ∆G2 = 0.

122			Г л а в а 2. Приложения химической термодинамики
	Поскольку
			∂∆G				2	P2
			∂∆G		= ∆V , то ∫d ∆G =			∫ ∆Vdp = ∆G2 – ∆G1 = ∆V(p2 – p1).
			∂p		= ∆V , то ∫d ∆G =			∫ ∆Vdp = ∆G2 – ∆G1 = ∆V(p2 – p1).
			∂p	T			1	P
								1
	Отсюда
	p2 =	∆G2 − ∆G1				+ p =	0 − 2900		+ 101325 = 1.52 109 Па = 1.5 104 атм.
	p2 =					+ p =			+ 101325 = 1.52 109 Па = 1.5 104 атм.
			∆V		1		−1.91 10	−6
			∆V				−1.91 10	−6

Ответ. p = 1.5 104 атм.

Пример 7-6. Температура кипения бензола при давлении 1 атм равна 80.1 °C. Оцените давление пара бензола при 25 °C.

Решение. Давление пара бензола при T1 = 353.3 K равно p1 = 1 атм. По правилу Трутона

∆испH = 88 353.3 = 31.1 кДж моль–1.

Подставим эти данные в уравнение (7.11.б). Получим:

ln	p2	=	31100	1	−	1	, откуда p2	= 0.141 атм.

	1			353.3		298.2
			8.314

Ответ. p = 0.141 атм.

ЗАДАЧИ

7-1. Система содержит химические элементы А, В, С, образующие в газовой фазе молекулы AB, A2B2, B2C и A3B2. Укажите компонентный состав системы.

7-2. Определите число компонентов и число независимых реакций в системе, состоящей из:

а) NH3, HCl, NH4Cl(г); б) O2, H2, H2O(г), H2O2(г);

в) H2, Cl2, Br2, HCl(г), HBr(г).

7-3. Определите число степеней свободы перечисленных систем:

а) CO, CO2, O2, H2, H2O(г);

б) CO, CO2, O2, H2, H2O(г), H2O(ж).

Как изменится вариантность систем (а, б), если:

1)системы находятся во внешнем поле;

2)в системе заторможены все химические превращения?

Г л а в а 2. Приложения химической термодинамики

123

7-4. На рисунке изображены температурные зависимости энергий Гиббса фаз германия. Определите, какая фаза будет термодинамически стабильна при температуре:

а) 700 К, б) 1500 К?

		l
0	S
G – H
300	500	700	900	1100	1300	1500	1700	1900

T(K)

7-5. На рисунке изображены температурные зависимости энергий Гиббса фаз фосфора. Определите, какая фаза будет термодинамически стабильна при температуре:

а) 500 К, б) 1300 К.

Какая фаза может существовать только как метастабильная?

	белый
0	красный
H	красный
–					черный
G					черный
G
300	500	700	900	1100	1300	1500

T(K)

7-6. Рассчитайте давление, при котором две формы CaCO3 – кальцит и арагонит – находятся в равновесии при 25 °C. ∆fG° кальцита и арагонита при 25 °C равны –1128.79 и –1127.75 кДж моль–1 соответственно. Примите, что плотности кальцита и арагонита равны 2.71 и 2.93 г см–3 соответственно, и не зависят от давления.

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 4812 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в папке 7 семестр

#
02.01.2023721.17 Кб28Лекции.docx
#
02.01.20233.78 Mб29Методичка - Химическая кинетика.pdf
#
02.01.20235.51 Mб78Основы_физич_химии_Теория_и_задачи_Еремин_и_др_2005_480с.pdf