
7 семестр / Основы_физич_химии_Теория_и_задачи_Еремин_и_др_2005_480с
.pdf34 |
Г л а в а 1. Основы химической термодинамики |
Для конденсированной фазы второе слагаемое в выражении (2.12) обычно мало, поэтому
(2.17) |
C p CV , C p,m CV ,m . |
Изохорная теплоемкость определяется через теплоту, переданную системе при постоянном объеме. Так как при постоянном объеме механическая работа не совершается, теплота равна изменению внутренней энергии δQV = dU = CVdT. При постоянном давлении теплота равна изменению другой функции состояния, которую называют эн-
тальпией:
(2.18) |
δQp = dU + pdV = d (U + pV) = dH, |
где H = U + pV – энтальпия системы.
Из последнего равенства следует, что изобарная теплоемкость Cp определяет зависимость энтальпии от температуры.
(2.19) |
Cp = |
∂H |
. |
|
|
∂T |
p |
Зависимость теплоемкости от давления или объема
(2.20)
(2.21)
(2.22)
Для определения вида зависимости изохорной теплоемкости некоторого вещества от объема необходимо найти производную CV по объему:
|
∂CV |
|
∂ |
∂U |
|
|
∂ |
∂U |
|
|||
|
|
|
= |
|
|
|
|
= |
|
|
|
. |
∂V |
|
|
||||||||||
|
T |
|
∂V |
∂T V T |
|
∂T |
∂V T V |
|||||
Аналогично, зависимость изобарной теплоемкости от давления можно выразить через производную:
∂C p |
|
∂ |
∂H |
|
|
∂ ∂H |
|
|||||
|
|
|
= |
|
|
|
|
= |
|
|
|
. |
|
|
|
||||||||||
∂p |
|
|
|
|
|
|
||||||
|
T |
|
∂p |
∂T p T |
|
∂T |
∂p T p |
|||||
Внутренняя энергия (энтальпия) идеального газа не зависит от объема (давления), поэтому
∂CV |
= 0 и |
|
∂C p |
= 0 , |
|||
|
|
T |
|
|
T |
||
∂V |
∂p |
||||||
т.е. теплоемкость идеального газа не зависит от V и p. Для реальных газов и конденсированной фазы эта зависимость становится заметной только при очень больших давлениях.

Г л а в а 1. Основы химической термодинамики |
35 |
ПРИМЕРЫ
Пример 2-1. Рассчитайте изменение внутренней энергии гелия (одноатомный идеальный газ) при изобарном расширении от 5 до 10 л под давлением 196 кПа.
Решение. p1 = p2 = 196 кПа, V1 = 5 л, V2 = 10 л. Начальная и конечная температуры: T1 = p1V1 / nR, T2 = p2V2 / nR. Изменение внутренней энергии идеального газа определяется только начальной и конечной температурами (CV = 3/2 nR – идеальный одноатомный газ):
∆U = CV (T2 – T1) = 3/2 nR (T2 – T1) =
=3/2 (p2V2 – p1V1) = 3/2 (196 103) (10 – 5) 10–3 = 1470 Дж.
Ответ. 1470 Дж.
Пример 2-2. Один моль ксенона, находящийся при 25 °С и 2 атм, расширяется адиабатически:
а) обратимо до 1 атм, б) против давления 1 атм.
Какой будет конечная температура в каждом случае? Решение. а) Исходный объем ксенона (n = 1):
V1 = nRT1 / p1 = 0.082 298 / 2 = 12.2 л.
Конечный объем можно найти из уравнения адиабаты (для одноатомного идеального газа γ = Cp / CV = 5/3):
p1V15/3 = p2V25/3
V2 = V1 (p1/p2)3/5 = 12.2 23/5 = 18.5 л.
Конечную температуру находим по уравнению состояния идеального газа (p2 = 1 атм):
T2 = p2V2 / nR = 18.5 / 0.082 = 225 К.
б) При необратимом расширении против постоянного внешнего давления уравнение адиабаты неприменимо, поэтому надо воспользоваться первым законом термодинамики. Работа совершается за счет убыли внутренней энергии:
–W = –∆U = nCV (T1 – T2),
где n = 1, CV = 3/2 R (одноатомный идеальный газ).
Работа расширения против постоянного внешнего давления p2 равна:
–W = p2 (V2 – V1) = nRT2 – p2V1.
Приравнивая последние два выражения, находим температуру T2:
T2 = (nCVT1 + p2V1) / (nCV + nR) = 238 К.

36 |
Г л а в а 1. Основы химической термодинамики |
Температура выше, чем при обратимом расширении, т.к. в обратимом случае совершается бόльшая работа, расходуется больше внутренней энергии и температура понижается на бόльшую величину.
Ответ. а) 225 К; б) 238 К.
Пример 2-3. Один моль водяных паров обратимо и изотермически сконденсировали в жидкость при 100 °С. Рассчитайте работу, теплоту, изменение внутренней энергии и энтальпии в этом процессе. Удельная теплота испарения воды при 100 °С равна 2260 Дж г–1.
Решение. В процессе
H2O(г) → H2O(ж)
произошло обратимое сжатие газа при постоянном давлении p = 1 атм от объема
V1 = nRT / p = 0.082 373 = 30.6 л
до объема одного моля жидкой воды V2 ≈ 0.018 л. Работа сжатия при постоянном давлении равна:
W = –p (V2 – V1) ≈ pV1 = 101.3 кПа 30.6 л = 3100 Дж.
При испарении одного моля воды затрачивается теплота
2260 Дж г–1 18 г = 40700 Дж,
поэтому при конденсации одного моля воды эта теплота, напротив, выделяется в окружающую среду:
Q = –40700 Дж.
Изменение внутренней энергии можно рассчитать по первому закону:
∆U = Q + W = –40700 + 3100 = –37600 Дж,
а изменение энтальпии – через изменение внутренней энергии:
∆H = ∆U + ∆(pV) = ∆U + p∆V = ∆U – W = Q = –40700 Дж.
Изменение энтальпии равно теплоте, т.к. процесс происходит при постоянном давлении.
Ответ. W = 3100 Дж, Q = ∆H = –40700 Дж, ∆U = –37600 Дж.
ЗАДАЧИ
2-1. Газ, расширяясь от 10 до 16 л при постоянном давлении 101.3 кПа, поглощает 126 Дж теплоты. Определите изменение внутренней энергии газа.
Г л а в а 1. Основы химической термодинамики |
37 |
2-2. Определите изменение внутренней энергии, количество теплоты и работу, совершаемую при обратимом изотермическом расширении азота от 0.5 до 4 м3 (начальные условия: температура 26.8 °С, давление
93.2 кПа).
2-3. Один моль идеального газа, взятого при 25 °C и 100 атм, расширяется обратимо и изотермически до 5 атм. Рассчитайте работу, поглощенную теплоту, ∆U и ∆H.
2-4. Рассчитайте изменение энтальпии кислорода (идеальный газ) при изобарном расширении от 80 до 200 л при нормальном атмосферном давлении.
2-5. Какое количество теплоты необходимо для повышения температуры 16 г кислорода от 300 до 500 К при давлении 1 атм? Как при этом изменится внутренняя энергия?
2-6. Объясните, почему для любой термодинамической системы Cp > CV.
2-7. Чайник, содержащий 1 кг кипящей воды, нагревают до полного испарения при нормальном давлении. Определите W, Q, ∆U, ∆H для этого процесса. Мольная теплота испарения воды 40.6 кДж моль–1.
2-8. Определите конечную температуру и работу, необходимую для адиабатического сжатия азота от 10 л до 1 л, если начальные температура и давление равны 26.8 °С и 101.3 кПа, соответственно.
2-9. Три моля идеального одноатомного газа (CV = 3.0 кал моль–1 К–1), находящегося при T1 = 350 K и p1 = 5 атм, обратимо и адиабатически расширяются до давления p2 = 1 атм. Рассчитайте конечные температуру и объем, а также совершенную работу и изменение внутренней энергии и энтальпии в этом процессе.
2-10. Система содержит 0.5 моль идеального одноатомного газа (CV = 3.0 кал моль–1 К–1) при p1 = 10 атм и V1 = 1 л. Газ расширяется обратимо и адиабатически до давления p2 = 1 атм. Рассчитайте начальную и конечную температуры, конечный объем, совершенную работу, а также изменение внутренней энергии и энтальпии в этом процессе. Рассчитайте эти величины для соответствующего изотермического процесса.
2-11. Рассчитайте количество теплоты, необходимое для нагревания воздуха в квартире общим объемом 600 м3 от 20 °С до 25 °С. Примите, что воздух – это идеальный двухатомный газ (CV,m = 5/2 R), а давление при исходной температуре нормальное. Найдите ∆U и ∆H для процесса нагревания воздуха.
2-12. Человеческий организм в среднем выделяет 104 кДж в день благодаря метаболическим процессам. Основной механизм потери этой энер-

38 |
Г л а в а 1. Основы химической термодинамики |
гии – испарение воды. Какую массу воды должен ежедневно испарять организм для поддержания постоянной температуры? Удельная теплота испарения воды равна 2260 Дж г–1. На сколько градусов повысилась бы температура тела, если бы организм был изолированной системой? Примите, что средняя масса человека составляет 65 кг, а теплоемкость равна теплоемкости жидкой воды.
2-13. Один моль паров брома обратимо и изотермически сконденсировали в жидкость при 59 °С. Рассчитайте работу, теплоту, изменение внутренней энергии и энтальпии в этом процессе. Удельная теплота испарения брома при 59 °С равна 184.1 Дж г–1.
Давление / атм
1 |
|
2-14. Один моль идеального |
|||
2 |
|
одноатомного газа вступает в |
|||
|
|
следующий замкнутый цикл: |
|||
|
|
Процесс 1 → 2 – изотер- |
|||
|
|
мический, 3 → 1 – адиабати- |
|||
|
|
ческий. |
Рассчитайте |
объемы |
|
|
|
системы в состояниях 2 и 3, а |
|||
1 |
|
также |
температуры |
состоя- |
|
2 |
ний 1, |
2 и 3, считая стадии |
|||
3 |
|||||
 1 → 2 и 3 → 1 обратимыми.
1 → 2 и 3 → 1 обратимыми.
22.4 |
|
Рассчитайте ∆U и ∆H для ка- |
|
Объем / л |
|
|
ждой стадии. |
|
|
|
2-15. Придумайте циклический процесс с идеальным газом, состоящий из четырех стадий. Изобразите этот процесс в координатах p – V. Рассчитайте полное изменение внутренней энергии, а также теплоту и совершенную газом работу.
2-16. Один моль фтороуглерода расширяется обратимо и адиабатически вдвое по объему, при этом температура падает от 298.15 до 248.44 К. Чему равно значение CV?
2-17. Докажите соотношение, приведенное в табл.2.1 для работы обратимого адиабатического процесса.
2-18. Один моль метана, взятый при 25 °С и 1 атм, нагрет при постоянном давлении до удвоения объема. Мольная теплоемкость метана дается выражением:
Cp = 5.34 + 0.0115 T (кал моль–1 К–1).
Рассчитайте ∆U и ∆H для этого процесса. Метан можно считать идеальным газом.
2-19. Один моль дифторметана (идеальный газ), взятый при 0 °С и 1 атм, нагрет при постоянном давлении до утроения объема. Рассчитай-

Г л а в а 1. Основы химической термодинамики |
39 |
те изменение энтальпии и внутренней энергии в этом процессе, если зависимость теплоемкости дифторметана от температуры имеет вид:
Cp = 20.26 + 7.59 10–2 T (Дж моль–1К–1).
2-20. Выведите уравнение для обратимого адиабатического сжатия неидеального газа, если уравнение состояния одного моля газа имеет вид:
p (V – b) = RT.
2-21. Используя уравнение состояния и первый закон термодинамики, выведите уравнение адиабаты для газа Ван-дер-Ваальса.
2-22. Четыре моля кислорода, находящиеся в объеме 20 л при температуре 270 К, подвергли адиабатическому расширению против внешнего давления 600 Торр до утроения объема. Рассчитайте конечную температуру, совершенную работу, изменение внутренней энергии и энтальпии.
2-23. Три моля идеального газа, находящиеся при температуре 200 К и давлении 2.0 атм, обратимо и адиабатически сжали до температуры 250 К. Рассчитайте конечные давление и объем, а также работу, изменение внутренней энергии и энтальпии. Изохорная теплоемкость газа равна 27.5 Дж моль–1К–1.
2-24. Определите изменение внутренней энергии одного моля гелия (идеальный газ) при нагревании от T1 до T2:
а) в изохорном процессе; б) в изобарном процессе;
в) в адиабатическом процессе.
В каком случае увеличение внутренней энергии будет наибольшим?
2-25. Кусочек цинка массой 5.0 г бросили в стакан с разбавленной соляной кислотой. Рассчитайте работу, совершенную системой в результате реакции. Атмосферное давление составляет 0.95 атм, а температура равна 23 °C.
2-26. Рассчитайте изменение внутренней энергии в реакции образования мочевины, если известно, что стандартная энтальпия этой реакции равна –333.51 кДж моль–1.
2-27. Изобразите приведенный на рисунке цикл для идеального газа в координатах: p – T, V – T, ∆U – T, ∆H – T, ∆U – V, ∆H – p.
p |
1 |
2 |
|
|
|
3 |
V |
40 |
Г л а в а 1. Основы химической термодинамики |
2-28. Изобразите приведенный на рисунке цикл для идеального газа в координатах: p – T, V – T, ∆U – T, ∆H – T, ∆U – V, ∆H – p.
p |
1 |
|
|
|
2 |
3 |
V |
§ 3. Термохимия
Термохимия изучает тепловые эффекты химических реакций. Во многих случаях эти реакции протекают при постоянном объеме или постоянном давлении. Из первого закона термодинамики следует, что при этих условиях теплота совпадает с изменением функции состояния. При постоянном объеме теплота равна изменению внутренней энергии:
(3.1) |
δQV = dU , QV = ∆U , |
а при постоянном давлении – изменению энтальпии:
(3.2) |
δQ p = dH , Qp = ∆H. |
Эти равенства в применении к химическим реакциям составляют суть закона Гесса:
Теплота химической реакции при постоянном объеме или давлении (тепловой эффект химической реакции) не зависит от пути проведения процесса, а определяется только состоянием реагентов и продуктов реакции при условии, что единственной работой, совершаемой системой, является механическая работа.
Тепловой эффект относят к Т = const.
Для обозначения изменения любой термодинамической функции при протекании химической реакции используют оператор химической реакции ∆r (r означает «reaction»), например, ∆rU, ∆rH, ∆rCp и т.д. Тепловой эффект химической реакции записывают как ∆rU или ∆rH в зависимости от условий проведения (V = const или p = const). Теплоту химической реакции при постоянном давлении иногда называют просто «энтальпией реакции».
В термохимии, в отличие от других приложений термодинамики, теплота считается положительной, если она выделяется в окружающую среду, т.е. для экзотермической реакции ∆rH < 0 или ∆rU < 0.

Г л а в а 1. Основы химической термодинамики |
41 |
Если реакция протекает в растворе или в твердой фазе, где изменение объема незначительно, то
∆rH = ∆rU + ∆r(pV) ≈ ∆rU. |
(3.3) |
Если же в реакции участвуют идеальные газы, то при постоянной температуре
∆rH = ∆rU + ∆r(pV) = ∆rU + ∆ν RT, |
(3.4) |
где ∆ν – изменение числа молей газов в реакции.
Тепловые эффекты зависят, в общем случае, от температуры и давления, поэтому для термохимических расчетов необходимо, чтобы все тепловые эффекты были отнесены к одинаковым условиям, т.е. стандартизованы. Стандартные состояния обозначают надстрочным индексом «°». В настоящее время приняты следующие стандартные состояния:
•для индивидуальных кристаллических и жидких веществ – реальное состояние (наиболее устойчивая модификация) при заданной температуре и давлении 1 бар;
•для индивидуальных газов – гипотетическое состояние, возникающее при изотермическом расширении газа до бесконечно малого давления с последующим сжатием до 1 бар, но уже по изотерме идеального газа (см. рис. 3.1).
Обычно поправка на
неидеальность |
при |
ат- |
p |
|
|
|
|
|
|
мосферном |
давлении |
|
|
|
|
|
|
||
мала, и ею пренебрега- |
p = 1 |
|
A B |
|
|
|
|||
ют. |
Поправку |
можно |
|
|
|
|
|
||
|
|
|
|
|
|
||||
учесть, если |
известно |
|
|
|
|
|
|
||
уравнение состояния ре- |
|
|
Ид.газ |
|
|
|
|||
ального газа. |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
Так как в конденси- |
|
|
|
|
|
|
||
рованной фазе процессы |
|
|
Реал.газ |
|
|
|
|||
диффузии заторможены |
|
|
|
|
|
|
|||
по сравнению с газовой |
|
|
|
|
|
|
|||
|
|
|
V |
|
|
||||
фазой, возможно суще- |
|
|
К понятию |
|
Рис. 3.1 |
||||
|
|
|
|
||||||
ствование при |
одних и |
|
«стандартное состояние газа» |
|
|
|
|||
|
|
|
|
||||||
тех же условиях (p,T) |
|
|
|
|
|
|
|||
как |
стабильных, так |
и |
|
|
|
|
|
|
|
метастабильных состояний вещества (например, графита и алмаза). Калометрические методы позволяют экспериментально определить свойства и тех и других фаз. Поэтому в термохимических уравнениях принято указывать не только формулы веществ, но и их агрегатные состояния или кристаллические модификации.
Энтальпию реакции между веществами, находящимися в стандартных состояниях при температуре T, называют стандартной энтальпией
реакции и обозначают ∆ r HTo.
42 |
Г л а в а 1. Основы химической термодинамики |
Стандартная энтальпия образования, ∆ f H To («f» означает «forma-
(3.5)
(3.6)
tion») – изобарный тепловой эффект реакции образования одного моля данного химического соединения из простых веществ в стандартных состояниях. Энтальпия образования простого вещества в стандартном состоянии равна 0 при любой температуре. Понятие «энтальпия образования» используют не только для обычных веществ, но и для ионов в растворе. При этом за точку отсчета принят ион H+, для которого стандартная энтальпия образования в водном растворе полагается равной нулю: ∆ f H To(H + ) = 0 .
Стандартная энтальпия сгорания ∆ c H To («c» означает «combus-
tion») – изобарный тепловой эффект реакции окисления одного моля вещества газообразным кислородом при p(O2) = 1 бар. Теплота сгорания, если не оговорено особо, отвечает окислению углерода до СО2, водорода до H2O(ж), для остальных веществ в каждом случае принято указывать образующиеся продукты.
Из закона Гесса вытекают важные следствия, которые позволяют рассчитывать энтальпии химических реакций.
Следствие 1. Стандартная энтальпия химической реакции
∑ν i Ai = ∑ν j B j
i |
j |
равна разности стандартных энтальпий образования продуктов реакции и реагентов (с учетом стехиометрических коэффициентов):
∆ r HTo = ∑ν j ∆ f HTo(B j ) − ∑ν i ∆ f HTo(Ai ) .
j |
i |
Следствие 2. Стандартная энтальпия химической реакции
∑ν i Ai = ∑ν j B j
i |
j |
равна разности стандартных энтальпий сгорания реагентов и продуктов реакции (с учетом стехиометрических коэффициентов):
∆ r HTo = ∑ν i ∆ c HTo(Ai ) − ∑ν j ∆ c HTo(B j ) .
i |
j |
Это следствие обычно используют для расчета тепловых эффектов органических реакций.
Энтальпию химической реакции можно также рассчитывать по разности энергий разрываемых и образующихся химических связей. Энергией связи A–B называют энергию, необходимую для разрыва связи и разведения образующихся частиц на бесконечное расстояние:
AB(г) → A(г) + B(г).
Энергия связи всегда положительна.
Г л а в а 1. Основы химической термодинамики |
43 |
Большинство термохимических данных в справочниках приведено при температуре 298 К. Для расчета тепловых эффектов при других температурах используют уравнение Кирхгофа:
|
d ∆ r H |
= ∆ r C p (дифференциальная форма), |
(3.7.а) |
|
|
dT |
|||
|
|
T2 |
|
|
|
|
|
|
|
∆ r HT2 = ∆ r HT1 |
+ ∫ ∆ r C p (T )dT (интегральная форма). |
(3.7.б) |
||
|
|
|
T1 |
|
где ∆ r Сp = ∑ν j Сp (B j ) − ∑ν i C p (Ai ) – разность изобарных тепло- |
|
|||
j |
|
i |
|
|
емкостей продуктов реакции и исходных веществ.
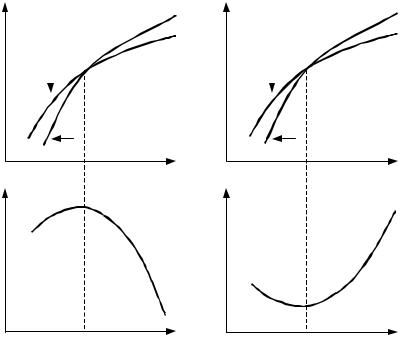
Если разница T2 – T1 невелика, то можно принять ∆rCp = const. При большой разнице температур необходимо учитывать температурную зависимость ∆rCp(T). В отличие от теплоемкостей участников реакции, разность ∆rCp(T) может быть и положительной, и отрицательной. При этом изменение ∆rH с температурой определяется видом зависимости ∆rCp(T) (см. рис. 3.2).
Сp |
|
|
Сp |
|
|
|
продукты |
реагенты |
|||||
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
реагенты |
продукты |
|
|
T |
T |
∆rH |
∆rH |
T |
T |
Различные виды зависимости ∆rCp и ∆rH от температуры |
Рис. 3.2 |
Теплоемкость – экспериментально измеряемая экстенсивная величина. В термодинамических таблицах обычно табулируют значения мольной теплоемкости с шагом в 100 К, либо приводят величины Cp при 298 К и коэффициенты полинома, описывающего ее зависимость от
