
- •Кинетика сложных химических реакций
- •Кинетика обратимых реакций
- •Параллельные реакции
- •Последовательные реакции
- •Приближенные методы химической кинетики (квазистационарная)
- •Квазиравновесное приближение
- •Катализ
- •Кислотно-основный катализ
- •Уравнение изотермы адсорбции Ленгмюра
- •Механизмы процесса адсорбции
Химическая кинетика - раздел физхимии, изучающий скорость и раздел химических реакций. Химическая реакция – «последовательность» стадий. Основные задачи хим. кинетики: 1) расчет скоростей реакций и определение кинетических кривых, т.е. зависимости конц. реагирующих ве-в от времени (прямая задача); 2) определение механизмов реакций по кинетическим кривым (обратная задача). Основные различия между хим. т/д и кинетикой: 1. В хим. т/д нет времени, она предсказывает только конечный результат процесса. Хим. кинетика изучает только изменяющиеся (динамические) системы. 2. Равновесные св-ва определяется состоянием как исх. ве-в, так и продуктов реакции. Для т/д важны левая и правая части хим. уравнения. Скорость реакции определ. только состоянием исх. ве-в. Для кинетики важна только левая часть уравнения реакции. 3. Т/д св-ва определяются т/д активностью ве-в, кинетические св-ва – их конц.
|
Скорость
реакции (r)-изменение
конц. в единицу времени: r=
|
A 2B
скорости одинаковые до знака и до
константы.
2B
скорости одинаковые до знака и до
константы.
Факторы,
влияющие на скорость реакции (гомогенные
хим. реакции): природа реагирующих ве-в;
t;
конц.; cat.
Влияние
конц. на скорость хим. реакции
По
закону действующих масс (Скорость
хим. реакции в каждый момент времени
пропорциональна текущим конц. реагирующих
ве-в, возведенным в некоторые степени):
xA
+yB
=pC.
r
определяем по изменению конц. исх. ве-в.
r=k Константа
скорости (-одна из 3 фундаментальных
характеристик каждой реакции) реакции
зависит: природы; cat;
t.
Для некоторого класса наиболее
важных реакций k
имеется в таблицах, измеренных при
298К.
Основной задачей явл. нахождение
зависимости конц. от времени, чтобы
определить конц. ве-в в любой момент
времени. m,n-частные
порядки реакций по данному ве-ву (если
r
зависит от С данных ве-в); m+n-порядок
реакции.
Константа
скорости (-одна из 3 фундаментальных
характеристик каждой реакции) реакции
зависит: природы; cat;
t.
Для некоторого класса наиболее
важных реакций k
имеется в таблицах, измеренных при
298К.
Основной задачей явл. нахождение
зависимости конц. от времени, чтобы
определить конц. ве-в в любой момент
времени. m,n-частные
порядки реакций по данному ве-ву (если
r
зависит от С данных ве-в); m+n-порядок
реакции.
Различают реакции: нулевого, 1-ого, 2-ого, 3-его, дробных порядков. Чаще всего дело имеют с реакциями 1-ого и 2-ого порядков, реже 0-ого, ещё реже 3-его.
0
порядок: скорость этих реакций не зависит
от концентрации. –dC/dτ=k0;
dC=
- k0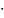 dτ;
dτ;
 ;
C
= - k0τ+const;
k0=1/τ
(C0-C)
;
C
= - k0τ+const;
k0=1/τ
(C0-C)
1
порядок: ЗАВИСИМОСТЬ КОНЦ. ОТ ВРЕМЕНИ
в реакциях типа A
-> B
скорость прямо пропорциональна конц.
–dC/dτ=k1
с1;
по методу разделения переменной: –dC/C=kⅠ
dτ;
 =
=
 dτ;
lnC=
- kⅠ
τ
+ const;
начальные условия реакции τ=0, С=С0,
тогда lnC0=
- kⅠ
0+const;
lnC0=
const;
const=
lnC0,
подставим и получим lnC=-
kⅠ
τ+lnC0;
kⅠ=1/r
ln(C0/C)
– ур. констант скорости 1-ого порядка
dτ;
lnC=
- kⅠ
τ
+ const;
начальные условия реакции τ=0, С=С0,
тогда lnC0=
- kⅠ
0+const;
lnC0=
const;
const=
lnC0,
подставим и получим lnC=-
kⅠ
τ+lnC0;
kⅠ=1/r
ln(C0/C)
– ур. констант скорости 1-ого порядка
2
порядок: ЗАВИСИТ ОТ ОДНОГО ВЕ-ВА – dC/dτ
= kⅡ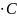 2;
- dC/C2
= kⅡ
dτ;
2;
- dC/C2
= kⅡ
dτ;
 =
=
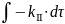 ;
;
 =
=
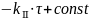 ;
;
 ;
;
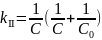 – ур. 2-ого пор.
– ур. 2-ого пор.
РЕШЕНИЕ
КИНЕТИЧ. УР. ДЛЯ СЛУЧАЯ, КОГДА R
ЗАВИСИТ ОТ С ДВУХ ВЕ-В (СA
и
CB
одинаковы) r=kⅡ (C0,
A=
C0,
B=a);
- dC/dτ
= kⅡ
2;
- dC/C2
= kⅡ
dτ;
=
;
=
(C0,
A=
C0,
B=a);
- dC/dτ
= kⅡ
2;
- dC/C2
= kⅡ
dτ;
=
;
=
 ;
;
;
;
3
порядок: – dC/dτ
= kⅢ
3A;
- dC/C3
= kⅢ
dτ;
 =
=
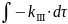 ;
const=
- 1/2С02;
;
const=
- 1/2С02;
 =
=
 ;
;
 ;
;
 =>
=>
 – ур. 3-ого пор.
– ур. 3-ого пор.
Методы определения констант скорости Чтобы определить экспериментально какую-то величину с высокой степенью точности необходимо достаточно большое число экспериментальных данных (min 6-7 точек). Нельзя строить и определять по 2-3 точкам.
1) Метод подстановки/Аналитический – заключается в подстановке экспериментальных данных в уравнения всех порядков.
r зависит от: природы и t. Там, где r не просматривается явная зависимость от конц. В столбце, где не просматривается явное влияние на константу скорости, там и правильная константа и можно найти среднюю: k={k/n. Недостатки: много расчетов.
2)
Графический – точнее, чем аналитический.
Наиболее просто поддается компьютер-ной
обработке. Заключается в том, что
необходимо имеющиеся зависимости c=f(τ)
представить в линейном виде. Изначально
уравнение: -dC/dτ
= k0
k0:
c=f(τ)
описывается линейной. k0=
1/τ
(C0-C)
C=
C0
- k0

Метод графический заключается в том, что необходимо представить эксперимен-тальные данные в соответствующих координатах (т.е. построить 4 графика) и выбрать функцию линейно зависящую от времени и затем из этого графика найти константу скорости.
3) Определить константы скорости по периоду полупревращения: Период полупревращения (τ1/2) – время, за которое подвергается превращению (расходуются/образуются) ровно 50% вещества. Для этого необходимо знать C0. Нужно знать порядок реакции, чтобы найти τ1/2. Найти связь между τ1/2 и k для реакций разных порядков.
Методы определения порядка ре-ции Методы основаны на тех же подходах и уравнениях. Методы подразделяют на интегральные (метод подстановки, метод Оствальда-Нойеса и полупревращения) и дифференцированные (метод Вант-Гоффа).
1) Метод подстановки: суть метода заключается в подстановке экспериментальных данных в уравнение для k разных порядков и получают массив констант скорости в том столбце, где k не имеет явного роста или убывания порядок реакции соответствует истинному. Если ни одно из кинетических уравнений не дает удовлетворительного результата, т.е. порядок реакции не является целым, это означает, что реакция описывается более сложным кинетическим уравнением. Метод подстановки дает надежные результаты для больших значений степени превращения.
2) Графический: заключается в подборе функции конц., линейно зависящий от времени. Если концентрация от времени линейна, то 0 порядок:
3) По периоду полупревращения: исп. полученное ур., связывающие к скорости и период полупревращения и для реакций разных порядков оказывается, что τ1/2 по-разному зависит от C0. Необходимо экспериментально найти τ1/2 при разных начальных конц., тогда, если: n=0 => τ1/2 изменяется от начальной конц., увеличивается с константой скорости n=1 => τ1/2 не зависит от C0 n=2 => τ1/2 линейно зависит от 1/ C0
4) Метод Вант-Гоффа: ограничения *скорость реакции должна зависеть только от конц. одного вещества; *имеется какая-либо независимая возможность непосредственного определения скорости реакция.
|
A
+ Bизб.
-> C
тогда r
не зависит от конц. B.
r=ΔС/τ
r=k |
n и k – фундаментальные константы
5) Метод Оствальда: если кинетическое уравнение имеет вид r=k[A]a[B]b, то исп. данный метод для определения порядка реакции по каждому из веществ или метод понижения порядка реакции. Суть метода: зависимость скорости реакции от начальной конц. одного из реагентов (например, A) изучают при большом избытке второго реагента. В таком случае конц. реагента B в течение реакции остается практически постоянной: r=k*[A]a, где k*= k[B]b. Порядок реакции a по веществу A находят один из перечисленных ранее методов. Затем так же для вещества B. Можно также определить порядки реакции сразу по обоим реагентам. Для этого логарифмируют уравнение и получают lnr=lnk+a ln[A]+b ln[B], подставляют значение скорости при разных значениях концентраций обоих реагентов и определяют порядки реакции a и b с помощью компьютерного регрессионного анализа. Влияние t на скорость ре-ции
Скорость
большинства реакций увеличивается с
ростом температуры, т.к. при этом
возрастает энергия сталкивающихся
частиц и повышается вероятность того,
что при столкновении произойдет хим.
превращение. Для количественного
описания темпера-турных эффектов в хим.
кинетике исп. два основных соотношения
– правило Вант-Гоффа и ур. Аррениуса.
Правило Вант-Гоффа (парабола)
заключается в том, что при нагревании
на 10 °С скорость большинства химических
реакций увеличивается в 2 ÷ 4 раза.
Математически это означает, что скорость
реакции зависит от температуры степенным
образом:
 =
=
 => r(T2)=r(T1)
=> r(T2)=r(T1)
 Правило
Вант-Гоффа довольно грубо описывает
экспериментальные данные и применимо
только в очень ограниченном интервале
температур.
Правило
Вант-Гоффа довольно грубо описывает
экспериментальные данные и применимо
только в очень ограниченном интервале
температур.
Гораздо более точным является уравнение Аррениуса, описывающее температурную зависимость константы скорости: ln(k) = -Eакт./RT + A, где A – предэкспоненциальный множитель, который не зависит от температуры, а определяется только видом/типом реакции, и его можно интерпретировать, как долю молекул, энергия которых превышает Eакт. при температуре T; Eакт. не зависит от t (-это некоторая пороговая энергия, характеризующая высоту энергетического барьера на пути к ре-ции), согласно Аррениусу – это избыток энергии по сравнению со средней величиной энергии молекул, которым должны обладать реагирующие частицы, чтобы они могли вступать в хим. ре-цию. Аррениус указал, что не каждое столкновение молекул приводит к хим. взаимодействию. Эффективными будут столкновения лишь между активными частицами. Активные молекулы – молекулы, обладающие повышенным запасом энергии по сравнению со средней энергией молекул тех же ве-в. Еакт. не зависит от t.
1)
Ре-ция протекает при столкновении
молекулы; 2) Число столкновений зависит
от скорости движения молекул: Uдвиж.=B ,
где B
– const
для молекулы одной природы.
С
увеличением t
скорость реакции увеличивается, т.к.
число столкновений увеличилось. Но не
все столкновения приводят к хим. реакции,
а лишь некоторая их часть. Eдвиж.=
m
,
где B
– const
для молекулы одной природы.
С
увеличением t
скорость реакции увеличивается, т.к.
число столкновений увеличилось. Но не
все столкновения приводят к хим. реакции,
а лишь некоторая их часть. Eдвиж.=
m /2
Все молекулы имеют разную
энергию
/2
Все молекулы имеют разную
энергию
Молекулы с большими энергиями - активные молекулы.
Э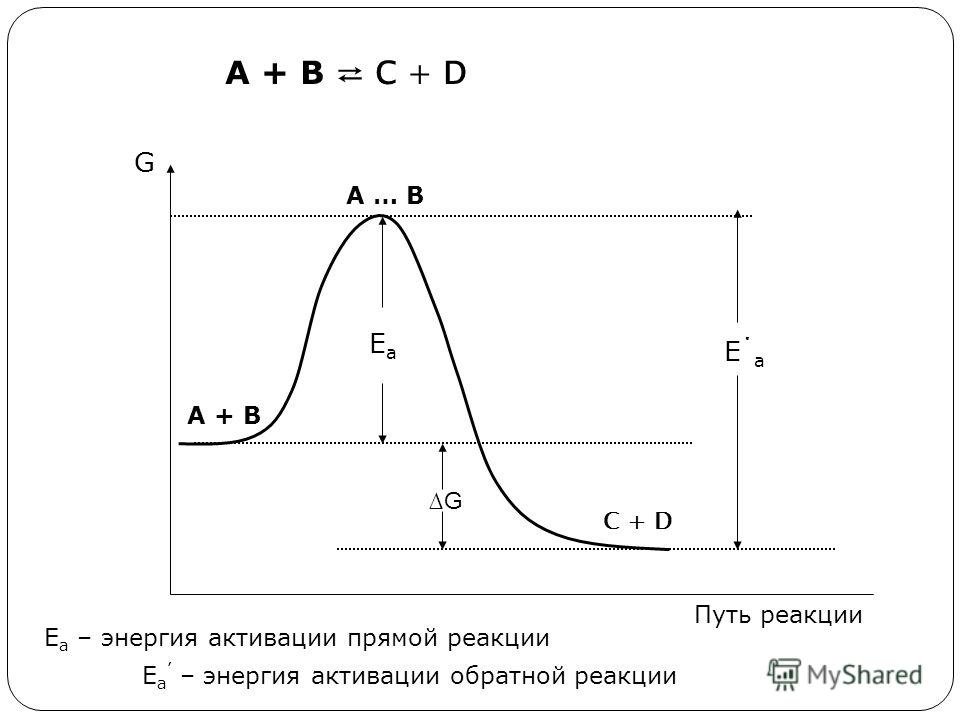 нергия
активации – это та энергия, которой
должны обладать молекулы (по сравне-нию
со средней энергией молекулы), чтобы их
столкновения приводили к хим. ре-циям.
нергия
активации – это та энергия, которой
должны обладать молекулы (по сравне-нию
со средней энергией молекулы), чтобы их
столкновения приводили к хим. ре-циям.
A+B↔C+D
Еа-энергия активации прямой реакции; Еа’-энергия активации обратной реакции. Процесс протекает с выделением теплоты «закон сохранения энергии» lnk= -Eакт./RT + A
Eакт. на ряду с порядком реакции и константой скорости является основной фундамен-тальной характеристикой каждой хим. реакции и зависит от природы реагирующих веществ и не зависит ни от температуры, ни от концентрации.
М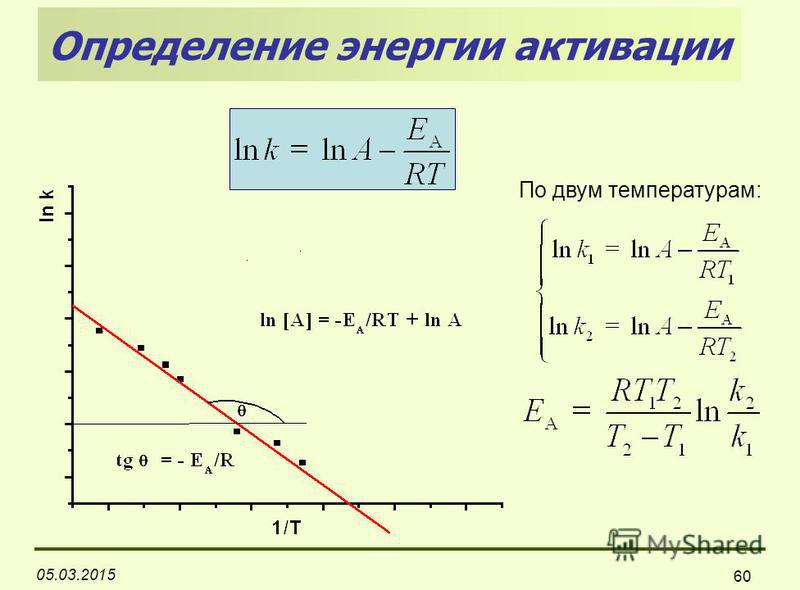 етоды
определения энергии активации:
1)
Расчетный: необходимо определить
экспериментально два значения констант
скорости при двух температурах. T2>T1,
Eакт.
должна быть положительна.
lnk1=
-Eакт./RT1
+ A
lnk2=
-Eакт./RT2
+ A
из 2-ого уравнения вычитают
первое:
ln(k2/k1)
= -Eакт./RT1
+ Eакт./RT2;
ln(k2/k1)
= -Eакт./R
(1/T2
– 1/T1);
Eакт.
= ln(k2/k1)
R
(1/T1
- 1/T2)
=> Eакт.
= ln(k2/k1)
R
((T2
T1)/
(T2
– T1))
[кДж/моль]
2) Графический: необходимо
определить 6-7 значений констант скорости
при нескольких температурах и затем
ур. Аррениуса представить в линейном
виде
Ур. Аррениуса – это зависимость
константы скорости реакции от температуры
и величины энергии активации.
етоды
определения энергии активации:
1)
Расчетный: необходимо определить
экспериментально два значения констант
скорости при двух температурах. T2>T1,
Eакт.
должна быть положительна.
lnk1=
-Eакт./RT1
+ A
lnk2=
-Eакт./RT2
+ A
из 2-ого уравнения вычитают
первое:
ln(k2/k1)
= -Eакт./RT1
+ Eакт./RT2;
ln(k2/k1)
= -Eакт./R
(1/T2
– 1/T1);
Eакт.
= ln(k2/k1)
R
(1/T1
- 1/T2)
=> Eакт.
= ln(k2/k1)
R
((T2
T1)/
(T2
– T1))
[кДж/моль]
2) Графический: необходимо
определить 6-7 значений констант скорости
при нескольких температурах и затем
ур. Аррениуса представить в линейном
виде
Ур. Аррениуса – это зависимость
константы скорости реакции от температуры
и величины энергии активации.
Кинетика сложных химических реакций
Практически все сколь угодно сложные механизмы реакций можно представить комбинацией трех базовых, качественно различных типов реакций: 1) обратимые, 2) параллельные, 3) последовательные.
Кинетика обратимых реакций
В качестве очень грубой границы между обратимыми и необратимыми реакциями можно принять значение константы равновесия K = 100, когда равновесные концентрации продукта и реагента различаются на два порядка. Рассмотрим кинетику обратимой реакции первого порядка:
![]()

где -степень
превращения пи достижении равновесия
-степень
превращения пи достижении равновесия
СоА – а; СоВ – B
Х - степень превращения
Текущая концентрация A = a - x; Текущая концентрация B = b + x;
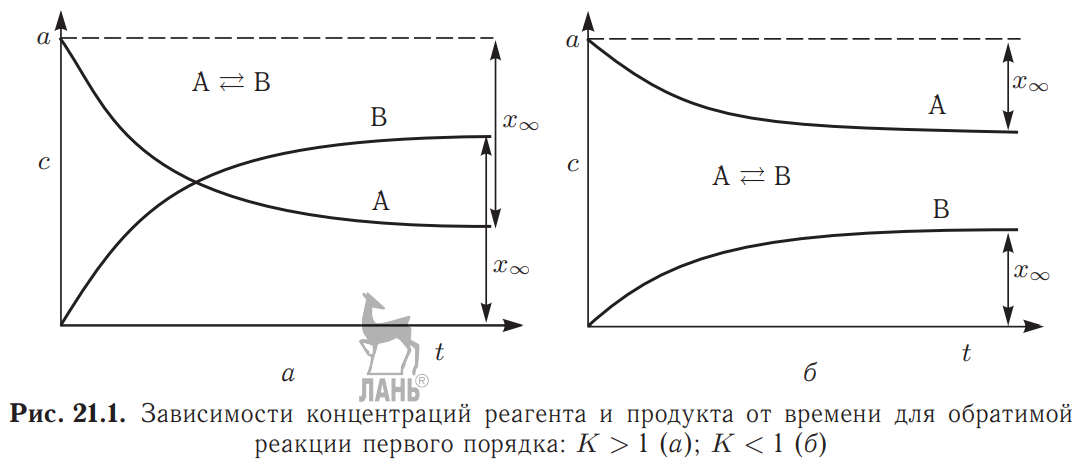
Состояние химического равновесия – это такое состояние, когда концентрации веществ остаются постоянными, а соответственно скорости не изменяются.
rпрям=k1САтек=k1(a - )
rобр=k2САтек=k2(b - )
k1a (a - x∞) = k2(b + x∞)
k1-k1x∞=k2b-k2x∞
x∞(-k2-k1) = k2b-k1a


Реакции протекают до тез пор, пока не устанавливается химическое равновесие:
Концентрации во время установления равновесия:
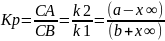
Параллельные реакции
Параллельные, или конкурирующие, реакции характерны для органической химии; нередко в этих реакциях наряду с основным веществом образуются побочные продукты.


k1+k2 =1/t*ln(a/a-x) –имеет 1-ый порядок по степени превращения, с константой скорости равной 2 константам
CAтек = a-x = a exp[-(k1+k2)t]
rобрB= k1CAтек=k1aexp[[-(k1+k2)t]
rобрD= k2CAтек=k2aexp[[-(k1+k2)t]
CB= 1-
exp[-(k1+k2)t]
1-
exp[-(k1+k2)t]
CD= 1-
exp[-(k1+k2)t]
→
1-
exp[-(k1+k2)t]
→
 – отношения концентрация продуктов
реакции остаются постоянными в любой
момент времени
– отношения концентрация продуктов
реакции остаются постоянными в любой
момент времени

Последовательные реакции
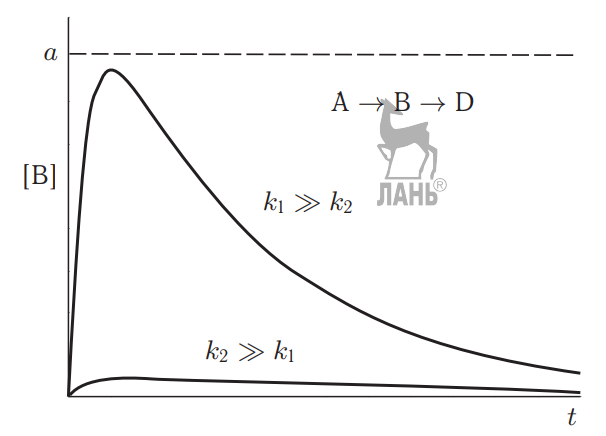
Необратимые последовательные реакции первого порядка — одна из самых широко распространенных моделей при изучении зависящих от времени систем. Рассмотрим простейшую схему, включающую всего две реакции:
![]()
Пусть в t0: C0A=a; C0B=0; C0D. Тогда
CA=a
exp(-k1t);
CB=a ;
CD=a-CA-CB
;
CD=a-CA-CB
Это означает, что кинетическая кривая продукта D имеет Sобразную форму с перегибом. До точки перегиба продукт D накапливается:

CB=a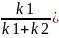 СА/СB=(k2-k1)/k1
СА/СB=(k2-k1)/k1
Поскольку большинство реакций являются сложными, протекающими в несколько стадий, включающие в том числе и обратимые, пар-ые, и посл-ые реакции, то даже сама система кинетических уравнений оказывается сложной для аналитического решения. Поэтому во многих случаях решение можно получить только, методами численного интегрирования. В то же время, константы скорости отдельных стадий могут различаться, на несколько порядков, что позволяет использовать методы приближенных химических расчетов.
Приближенные методы химической кинетики (квазистационарная)
CA=a exp(-k1t); CB=a ; CD=a-CA-CB
Если константы различаются значительно (2 порядка и более), то тогда можно упростить:
k2>>k1
→ CB=a
Зависимость концентрации от времени для всех веществ определяется только одной константой – k1 (самая медленная). Этот принцип называется – принципом лимитирующей стадии, те скорость образования и расходования всех веществ в системе определяется скорость самой медленной стадии в случае последовательных реакций (сколько бы не было стадий).
r1=k1CA r2=k2CB r1=k1a r2=k2a
r1=r2 => r2=k1a
Оказалось, сто скорость образования промежуточного продукта почти равна скорости его расходования, те остается практически постоянной. В этих условиях концентрацию промежуточного вещества считают квазистационарной.
Достоинства подхода квазистационарности – позволяет определить концентрации промежуточных веществ через концентрации исходных веществ.
Хотя
приближенно r1
и r2
равны, но они изменяются со временем.
Если сравнить концентрацию В, вычисленного
точно и с помощью квазистационарного
приближения, то видно,
что приближение начинает хорошо работать
лишь через небольшое время после начала
реакции. Оценить это время можно из
следующих соображений. t1=


 dc/dr.
Знак
плюс используют, если скорость
определяют по продукту, а минус – по
исходному веществу.
Для исх. и
продукта r
будут различаться: исх. прод.
dc/dr.
Знак
плюс используют, если скорость
определяют по продукту, а минус – по
исходному веществу.
Для исх. и
продукта r
будут различаться: исх. прод. => lnr
= ln(k
)
=> lnr
= lnk
=> lnr
= ln(k
)
=> lnr
= lnk => lnk
=> lnk