
7 семестр / Основы_физич_химии_Теория_и_задачи_Еремин_и_др_2005_480с
.pdf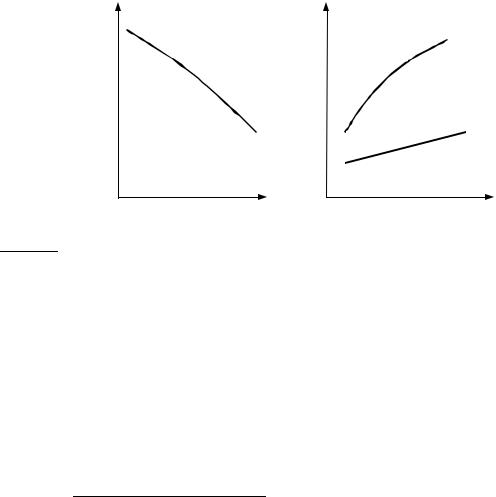
74 |
Г л а в а 1. Основы химической термодинамики |
(5.10.а)
(5.10.б)
Функции F и G являются функциями состояния, для них:
|
∂F |
= −SV , |
|
|
|
|
∂T V |
|
|
∂G |
= −Sp . |
|
|
|
|
∂T p |
|
Для интегрирования этих уравнений надо знать температурную зависимость энтропии, которая определяется теплоемкостью системы (формулы (4.21.а)). График зависимости энергии Гиббса1 от температуры в предположении линейной температурной зависимости теплоемкости приведен на рис. 5.2.а.
|
(а) |
G–H0 |
G–H0 |
|
T |
(б)
газ
конд. фаза
p
Рис. 5.2
(5.11.а)
(5.11.б)
Зависимость энергии Гиббса:
(a) от температуры при p = const, (б) от давления при T = const
2. Изменение энергий Гиббса и Гельмгольца при изотермическом расширении или сжатии
Зависимость энергии Гиббса и Гельмгольца от давления и объема при постоянной температуре может быть определена интегрированием
производных: |
|
|
∂F |
= − p , |
|
|
|
|
∂V T |
|
|
|
∂G |
= V . |
|
|
|
|
∂p T |
|
1 Энергия Гиббса вещества отсчитана относительно условно выбранного уровня H0.

Г л а в а 1. Основы химической термодинамики |
75 |
Для восстановления вида этой зависимости необходимо знать урав- нение состояния фазы. Так, для идеального газа
V |
nRT |
||
F(V2 ) − F(V1) = − ∫2 |
|||
V |
|||
V |
|||
1 |
|
|
|
p |
nRT |
||
G( p2 ) − G( p1) = ∫2 |
|
||
|
p |
||
p1 |
|||
dV = nRT ln V1 , V2
dp = nRT ln p2 . p1
Если p1 = p° = 1 бар, то говорят о стандартной энергии Гиббса, G°
G( p) − G o ( p o ) = nRT ln p .
На рис. 5.2.б приведены графики зависимости энергии Гиббса от давления при T = const для конденсированной фазы и газа.
3. Изменение энергий Гиббса и Гельмгольца при химической реакции
Расчет изменения функций F и G в химических реакциях можно проводить разными способами. Рассмотрим три из них на примере энергии Гиббса.
I. По определению, G = H – TS. Если продукты реакции и исходные вещества находятся при одинаковой температуре, то изменение энергии Гиббса в химической реакции
∑νi Ai = ∑ν j B j i j
(5.12.а)
(5.12.б)
(5.12.в)
равно
∆rGT = ∑ν jGj (T ) − ∑νiGi (T ) = ∆r HT − T ∆r ST . |
(5.13.а) |
|
j |
i |
|
В стандартных условиях |
|
|
∆rGTo = ∑ν jGoj |
(T ) − ∑νiGio (T ) = ∆r HTo − T ∆r STo . |
(5.13.б) |
j |
i |
|
II. Аналогично тепловому эффекту реакции, изменение энергии Гиббса можно рассчитать, используя стандартные энергии Гиббса образования реагентов и продуктов:
∆rGTo = ∑ν j ∆f Goj |
(T ) − ∑νi ∆f Gio (T ) |
|
(5.14) |
||
j |
|
i |
|
|
|
или |
|
|
|
|
|
∆rGTo = ∑ν j ∆f H oj |
|
|
− |
∑νi Sio |
|
− ∑νi ∆f Hio − T ∑ν j Soj |
. |
||||
j |
i |
j |
|
i |
|
Для расчета ∆rG при условиях, отличных от стандартных, используют соотношение (5.11.б).

76 |
|
Г л а в а 1. Основы химической термодинамики |
|
|
Изменение энергии Гельмгольца химической реакции между иде- |
|
|
альными газами связано с энергией Гиббса |
(5.15) |
∆rG = ∆r F + ∆νRT , |
|
|
|
где ∆ν – изменение количества молей газообразных веществ в ходе ре- |
|
|
акции. Для реакций в конденсированной фазе при небольших давлениях |
(5.16) |
∆rG ∆r F . |
|
III. Стандартная энергия Гиббса реакции может быть рассчитана с помощью стандартных приведенных потенциалов:
(5.17.а)
(5.17.б)
(5.18.а)
(5.18.б)
Фo(T ) = − Go(T ) − H o(0) ,
T
Ф′o(T ) = − Go(T ) − H o(298) ,
T
где G°(T) – стандартное значение энергии Гиббса при температуре Т, H°(0), H°(298) – стандартные значения энтальпии при температурах 0 и 298 К.
Функции Ф°(T) и Ф′°(T) вычисляются для газов по молекулярным данным, а для конденсированных фаз – на основании экспериментальных данных по теплоемкости. Связь между приведенными потенциалами и стандарной энергией Гиббса реакции выражается соотношениями:
|
|
|
|
|
|
|
+ ∆ r H o (0) |
|
∆ rG o (T ) = −T ∆ rФo (T ) + ∆ r H o (0) = −T ∑ν jФoj |
−∑ν iФio |
, |
||||||
|
|
|
j |
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
∆ rG o (T ) = −T ∆ rФ′o (T ) + ∆ r H o (298) = |
|
|
|
|||||
|
|
|
|
+ ∆ r H o (298) |
, |
|
|
|
= −T |
∑ν jФ′jo −∑ν iФi′o |
|
|
|
||||
|
j |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где ∆rH°(0), ∆rH°(298) – стандартные энтальпии реакции при 0 и 298 К.
ПРИМЕРЫ
Пример 5-1. Выполните преобразования Лежандра для функций: а) одной переменной y = cos(x),
б) двух переменных U = U (S,V).
Решение. Преобразования Лежандра являются примером так называемых контактных преобразований и имеют вид:
Х= x′ (х), Y(x) = xy′(x) – y(x), Y′(X) = x,
х= Y′(Х), y(x) = ХY ′(X) – Y(X), y′(x) = X.
Г л а в а 1. Основы химической термодинамики |
77 |
Преобразования Лежандра переводят одну функцию в другую, в которой одна или несколько независимых переменных заменены на соответствующие частные производные от первоначальной функции.
а) y = cos(x), (dy/dx) = –sin(x);
с точностью до знака Y(x) = cos(x) + x sin(x).
б) U = U (S,V), dU = TdS – pdV.
Чтобы перейти к другим переменным, например (S, p), надо к исходной функции прибавить pV:
U + pV ≡ H,
dH = dU + d(pV) = dU + pdV + Vdp = TdS – pdV + pdV + Vdp = TdS + Vdp.
Пример 5-2. Покажите, что из второго закона термодинамики следует уменьшение энергии Гиббса при протекании самопроизвольного процесса в закрытой системе при p,T = const. Примите, что отсутствуют все виды работ, кроме работы расширения.
Решение. Для обеспечения изотермичности система должна находиться в тепловом контакте с источником теплоты. Этот источник вместе с источником работы, который поддерживает постоянное давление на внешней границе системы, можно включить в расширенную изолированную систему. При протекании изобарно-изотермического процесса при Wпол = 0 изменение энтропии системы составит ∆Sист. В ходе процесса система получает (или отдает) теплоисточнику количество теплоты:
Qсист = ∆Hсист = – Qист,
∆Sист = − |
∆Hсист |
. |
|
||
|
T |
|
Общее изменение энтропии всех участников процесса в изолированной системе составит
∆Sобщ = ∆Scист − |
∆Hсист |
, dT = 0, dp = 0, Wпол = 0. |
|
||
|
T |
|
В соответствии со вторым законом термодинамики
∆Sобщ = ∆Scист − |
∆Hсист |
≥ 0 . |
|
||
|
T |
|
Последнее неравенство равносильно
∆Hсист − T ∆Scист ≤ 0 , ∆(H − TS)сист ≤ 0 , ∆Gсист ≤ 0 .
Пример 5-3. Внутренняя энергия некоторой системы известна как функция энтропии и объема, U(S,V). Найдите температуру и теплоемкость этой системы.
78 |
Г л а в а 1. Основы химической термодинамики |
Решение. Из основного уравнения термодинамики (5.1.а) следует, что температура – это частная производная внутренней энергии по энтропии:
|
∂U |
T = |
. |
|
∂S V |
Изохорная теплоемкость определяет скорость изменения энтропии с температурой:
|
|
∂S |
|
CV |
= T |
|
. |
|
|||
|
|
∂T V |
|
Воспользовавшись свойствами частных производных, можно выразить производную энтропии по температуре через вторую производную внутренней энергии:
|
|
|
|
|
|
|
|
|
|
|
∂U |
|||
|
|
T |
|
|
T |
|
|
|
|
|
|
|||
C = |
|
= |
|
|
= |
|
∂S V |
. |
||||||
|
∂T |
|
∂2U |
|
|
|||||||||
V |
|
|
∂2U |
|||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||
|
|
∂S |
|
∂S |
V |
|
|
∂S |
V |
|||||
|
|
|
V |
|
|
|
|
|||||||
Пример 5-4. Используя основное уравнение термодинамики, найдите зависимость энтальпии от давления при постоянной температуре:
а) для произвольной системы; б) для идеального газа.
Решение. а) Если основное уравнение в форме (5.1.б) поделить на dp при постоянной температуре, получим:
|
∂H |
|
∂S |
+ V . |
|
|
= T |
|
|
|
∂p T |
|
∂p T |
|
Производную энтропии по давлению можно выразить с помощью соотношения Максвелла (5.7.г):
|
∂H |
|
∂V |
+ V . |
|
|
= −T |
|
|
|
∂p T |
|
∂T p |
|
б) Для идеального газа V(T) = nRT / p. Подставляя эту функцию в последнее тождество, получим:
|
∂H |
nR |
|
nRT |
|
|||
|
|
= −T |
|
|
+ |
|
= 0 . |
|
p |
p |
|||||||
|
∂p T |
|
|
|
|
|||
Энтальпия идеального газа не зависит от давления.
Пример 5-5. Два моля гелия (идеальный газ, мольная теплоемкость Cp = 5/2 R) нагревают от 100 °С до 200 °С при p = 1 атм. Вычислите изменение энергии Гиббса в этом процессе, если известно значение эн-

Г л а в а 1. Основы химической термодинамики |
79 |
тропии гелия, S373o = 131.7 Дж К–1 моль–1. Можно ли считать этот процесс самопроизвольным?
Решение. Изменение энергии Гиббса при нагревании от 373 до 473 К можно найти, проинтегрировав частную производную по температуре
(5.10.б):
473
∆G = G473 − G373 = − ∫ S(T )dT .
373
Зависимость энтропии от температуры при постоянном давлении определяется изобарной темлоемкостью:
|
|
|
∂S |
|
Cp |
|
|
|
|
|
|
|
= |
|
. |
|
|
∂T |
T |
||||
|
|
|
|
p |
|
||
Интегрирование этого выражения от 373 К до T дает: |
|||||||
S(T ) = n S373o |
+ ∫ |
Cp dT |
= n (S373o + Cp ln T − Cp ln 373). |
||||
|
T |
|
|
|
|
|
|
|
373 |
T |
|
|
|
|
|
Подставляя это выражение в интеграл от энтропии, находим:
473 |
S(T )dT = −n (S373o |
− C p ln 373)T + C pT ln T − C pT |
373473 |
|
∆G = − ∫ |
= −26850 Дж. |
|||
373 |
|
|
|
|
|
|
|
|
Процесс нагревания не обязан быть самопроизвольным, т.к. уменьшение энергии Гиббса служит критерием самопроизвольного протекания процесса только при T = const и p = const.
Ответ. ∆G = –26850 Дж.
Пример 5-6. Рассчитайте изменение энергии Гиббса в реакции
CO + 1 O2 = CO2
2
при температуре 500 K и парциальных давлениях 3 бар. Будет ли эта реакция самопроизвольной при данных условиях? Газы считать идеальными. Необходимые данные возьмите из справочника.
Решение. Термодинамические данные при температуре 298 К и стандартном давлении 1 бар сведем в таблицу:
Вещество |
Энтальпия |
|
Энтропия |
|
Тепло- |
||||
образования ∆f H298o , |
o |
, Дж К |
–1 |
моль |
–1 |
емкость Cp, |
|||
|
|
|
кДж моль–1 |
S298 |
|
|
Дж К–1 моль–1 |
||
|
CO |
–110.5 |
|
197.6 |
|
|
29.14 |
||
|
O2 |
0 |
|
205.0 |
|
|
29.40 |
||
|
CO2 |
–393.5 |
|
213.7 |
|
|
34.57 |
||
Реакция |
∆r H 298o , кДж моль–1 |
∆r S298o , Дж К–1 моль–1 |
∆r C p , Дж К–1 моль–1 |
||||||
|
|
|
|
|
|
|
|
–9.27 |
|
CO + |
1 |
O2 = CO2 |
–283.0 |
|
–86.4 |
|
|
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
2 |
|
|
|
|
|
|
|
|
|

80 |
Г л а в а 1. Основы химической термодинамики |
∆ r H 500o
∆r S500o
Примем, что ∆rCp = const. Изменения термодинамических функций в результате реакции рассчитаны как разность функций реагентов и продуктов:
∆f = f(CO2) – f(CO) – 12 f(O2).
Стандартный тепловой эффект реакции при 500 К можно рассчитать по уравнению Кирхгофа в интегральной форме (3.7.б):
= ∆ r H 298o |
500 |
∆ rC p dT = − 283000 |
+ (−9.27) (500 − 298) = −284.9 кДж моль−1 . |
|||||
+ ∫ |
|
|||||||
|
298 |
|
|
|
|
|
|
|
|
Стандартное изменение энтропии в реакции при 500 К можно рас- |
|||||||
считать по формуле (4.22): |
|
|
||||||
= ∆r S298o + |
500 |
∆ |
C |
p |
|
|
|
|
∫ |
|
r |
|
dT = − 86.4 + (−9.27) ln(500/ 298) |
= −91.2 Дж моль−1 К−1 . |
|||
|
T |
|
||||||
|
298 |
|
|
|
|
|
||
Стандартное изменение энергии Гиббса при 500 К:
∆rG500o = ∆r H500o − 500∆r S500o = −284900 − 500 (−91.2) = −239.3 кДж моль−1.
Для расчета изменения энергии Гиббса при парциальных давлениях 3 атм необходимо проинтегрировать формулу (5.11.б) и использовать условие идеальности газов (∆V = ∆νRT / p, ∆ν – изменение числа молей газов в реакции):
p2
∆ rG( p2 ) = ∆ rG( p1) + ∫ ∆ rVdp = ∆ rG( p1) + ∆νRT ln( p2  p1) =
p1) =
p1
= − 240200 + (−0.5) 8.31 500 ln(3) = −242.5 кДжмоль−1.
Эта реакция может протекать самопроизвольно при данных условиях.
Ответ. ∆rG = –242.5 кДж моль–1.
ЗАДАЧИ
5-1. Выразите внутреннюю энергию как функцию переменных G, T, p.
5-2. Используя основное уравнение термодинамики, найдите зависимость внутренней энергии от объема при постоянной температуре:
а) для произвольной системы; б) для идеального газа.
5-3. Известно, что внутренняя энергия некоторого вещества не зависит от его объема. Как зависит давление вещества от температуры? Ответ обоснуйте.

Г л а в а 1. Основы химической термодинамики |
81 |
||||||||
5-4. Выразите производные |
|
∂p |
и |
|
∂p |
через другие термодина- |
|
||
|
|
|
|
|
|
|
|||
|
|
|
|||||||
|
|
∂G T |
|
|
∂T G |
|
|
||
мические параметры и функции.
5-5. Напишите выражение для бесконечно малого изменения энтропии как функции внутренней энергии и объема. Найдите частные производные энтропии по этим переменным и составьте соответствующее уравнение Максвелла.
5-6. Для некоторого вещества известно уравнение состояния p(V, T). Как изменяется теплоемкость CV с изменением объема? Решите задачу:
а) в общем виде; б) для какого-либо конкретного уравнения состояния (кроме иде-
ального газа).
5-7. Докажите тождество:
|
∂Cp |
|
∂2V |
|
|||
|
|
|
= −T |
|
2 |
. |
|
∂p |
∂T |
||||||
|
T |
|
|
p |
|||
5-8. Энергия Гельмгольца одного моля некоторого вещества записывается следующим образом:
F = a + T(b – c – b ln T – d ln V),
где a, b, c, d – константы.
Найдите давление, энтропию и теплоемкость CV этого вещества. Дайте физическую интерпретацию константам a, b, d.
5-9. Нарисуйте график зависимости энергии Гиббса индивидуального вещества от температуры в интервале от 0 до T > Tкип.
5-10. Для некоторой системы известна энергия Гиббса:
G(T,p) = aT(1 – lnT) + RT lnp – TS0 + U0,
где a, R, S0, U0 – постоянные.
Найдите уравнение состояния p(V,T) и зависимость U(V,T) для этой системы.
5-11. Зависимость мольной энергии Гельмгольца некоторой системы от температуры и объема имеет вид:
F = −cT lnT + dT − Va − RT ln(V − b) + F0 ,
где a, b, c, d – константы.
Выведите уравнение состояния p(V,T) для этой системы. Найдите зависимость внутренней энергии от объема и температуры U(V,T). Каков физический смысл постоянных a, b, c?
82 |
Г л а в а 1. Основы химической термодинамики |
5-12. Найдите зависимость мольной внутренней энергии от объема для термодинамической системы, которая описывается уравнением состояния (для одного моля)
p = |
RT |
1 |
+ |
B(T ) |
|
, |
|
V |
V |
||||||
|
|
|
|
|
где B(T) – известная функция температуры.
5-13. Для некоторого вещества зависимость теплоемкости от температуры имеет вид: CV = aT 3 при температуре 0 – 10 К. Найдите зависимость энергии Гельмгольца, энтропии и внутренней энергии от температуры в этом диапазоне.
5-14. Для некоторого вещества зависимость внутренней энергии от температуры имеет вид: U = aT 4 + U0 при температуре 0 – 10 К. Найдите зависимость энергии Гельмгольца, энтропии и теплоемкости CV от температуры в этом диапазоне.
5-15. Выведите соотношение между теплоемкостями:
Cp − CV = −T |
|
∂2G |
|
|
∂2 F |
|
|
||||||||
|
∂T 2 |
|
− |
∂T 2 |
|
. |
|
||||||||
|
|
|
|
p |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
V |
|
||||
5-16. Исходя из тождества |
Cp − CV = T |
∂p |
∂V |
, докажите тож- |
|||||||||||
|
|
|
V |
∂T T |
|||||||||||
∂T |
|||||||||||||||
дество: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂V 2 |
|
|
|
|
|
||||
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
||
C |
|
− C |
= − |
|
∂T p |
|
. |
|
|
|
|||||
|
|
∂V |
|
|
|
|
|
|
|||||||
|
p |
V |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
∂p |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
T |
|
|
|
|
|
|
|||
5-17. Один моль газа Ван-дер-Ваальса изотермически расширяется от объема V1 до объема V2 при температуре T. Найдите ∆U, ∆H, ∆S, ∆F и ∆G для этого процесса.
5-18. Вычислите изменение H, U, F, G, S при одновременном охлаждении от 2000 К до 200 К и расширении от 0.5 м3 до 1.35 м3 0.7 молей азота (CV = 5/2 R). Энтропия газа в исходном состоянии равна 213.4 Дж К–1 моль–1, газ можно считать идеальным.
5-19. Вычислите изменение энергии Гиббса при сжатии от 1 атм до 3 атм при 298 К:
а) одного моля жидкой воды; б) одного моля водяного пара (идеальный газ).
Г л а в а 1. Основы химической термодинамики |
83 |
5-20. Изменение энергии Гиббса в результате испарения воды при 95 °С и 1 атм равно 546 Дж моль–1. Рассчитайте энтропию паров воды при 100 °С, если энтропия жидкой воды равна 87.0 Дж К–1 моль–1. При каком давлении изменение энергии Гиббса в результате испарения воды будет равно 0 при 95 °С?
5-21. Изменение энергии Гиббса в результате испарения воды при 104 °С и 1 атм равно –437 Дж моль–1. Рассчитайте энтропию паров воды при 100 °С, если энтропия жидкой воды равна 87.0 Дж К–1 моль–1. При каком давлении изменение энергии Гиббса в результате испарения воды будет равно 0 при 104 °С?
5-22. Рассчитайте изменение энергии Гиббса в результате испарения воды при 97 °С и 1 атм, энтропия жидкой и газообразной воды при этой температуре равна 87.0 и 196.0 Дж К–1 моль–1, соответственно. При каком давлении изменение энергии Гиббса в результате испарения воды будет равно 0 при 97 °С?
5-23. Давление над одним молем твердой меди при температуре 25 °С увеличили от 1 до 1000 атм. Найти ∆U, ∆H, ∆S, ∆F. Медь считать несжимаемой, плотность 8.96 г см–3, изобарный коэффициент теплового
расширения |
1 |
|
∂V |
|
= 5.01 10–5 К–1. |
|
∂T |
||||
|
V |
p |
|||
5-24. Вычислите стандартную энергию Гиббса образования ( ∆f G298o ) жидкой и газообразной воды, если известны следующие данные:
∆f H 298o (H2O(г)) = –241.8 кДж моль–1,
∆f H 298o (H2O(ж)) = –285.6 кДж моль–1,
S298o (H2) = 130.6 Дж К–1 моль–1, S298o (O2) = 205.0 Дж К–1 моль–1,
S298o (H2O(г)) = 188.5 Дж К–1 моль–1, S298o (H2O(ж)) = 69.8 Дж К–1 моль–1.
5-25. Рассчитайте ∆G° при 25 °С для химической реакции:
4HCl(г) + O2(г) = 2Cl2(г) + 2H2O(ж).
Стандартные значения энтальпии образования и абсолютной энтро-
пии при 25 °С равны: |
|
∆fH°(HСl) = –22.1 ккал моль–1, |
S°(O2) = 49.0 кал К–1 моль–1, |
∆fH°(H2O(ж)) = –68.3 ккал моль–1; |
S°(Сl2) = 53.3 кал К–1 моль–1, |
S°(HCl) = 44.6 кал моль–1 К–1, |
S°(H2O(ж)) = 16.7 кал К–1 моль–1. |
5-26. Рассчитайте ∆G° при 25 °С для химической реакции: CO2(г) + 4H2(г) = CH4(г) + 2H2O(ж).
