Добавил:

Sahsha Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Тульский Государственный Университет

Предмет:

Физическая химия

Файл:

7 семестр / Основы_физич_химии_Теория_и_задачи_Еремин_и_др_2005_480с

.pdf

Скачиваний:

Добавлен:

02.01.2023

Размер:

5.51 Mб

Скачать

☆

<<< < Предыдущая 12 / 482 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

14Г л а в а 1. Основы химической термодинамики

•необратимые, или неравновесные, когда в результате процесса невозможно возвратить и систему, и ее окружение к первоначальному состоянию.

Входе процесса некоторые термодинамические переменные могут быть зафиксированы. В частности, различают изотермический (T = const), изохорный (V = const), изобарный (p = const) и адиабатический (Q = 0, δQ = 0) процессы.

Термодинамические функции разделяют на:

•функции состояния, которые зависят только от состояния системы и не зависят от пути, по которому это состояние получено;

•функции перехода, значение которых зависит от пути, по которому происходит изменение системы.

Примеры функций состояния: энергия U, энтальпия H, энергия Гельмгольца F, энергия Гиббса G, энтропия S. Термодинамические переменные – объем V, давление p, температуру T – также можно считать функциями состояния, т.к. они однозначно характеризуют состояние системы. Примеры функций перехода: теплота Q и работа W.

Функции состояния характеризуются следующими свойствами:

•бесконечно малое изменение функции f является полным дифференциалом (обозначается df);

•изменение функции при переходе из состояния 1 в состояние 2 оп-

ределяется только этими состояниями: ∫ df = f 2 − f1 ;

•в результате любого циклического процесса функция состояния не изменяется: ∫vdf = 0 .

Существует несколько способов аксиоматического построения термодинамики. В настоящем издании мы исходим из того, что выводы и соотношения термодинамики можно сформулировать на основе двух постулатов (исходных положений) и трех законов (начал).

Первое исходное положение, или основной постулат термодинамики:

Любая изолированная система с течением времени приходит в равновесное состояние и самопроизвольно не может из него выйти.

Это положение ограничивает размер систем, которые описывает термодинамика. Оно не выполняется для систем астрономического масштаба и микроскопических систем с малым числом частиц. Системы галактического размера самопроизвольно не приходят в состояние равновесия благодаря дальнодействующим гравитационным силам. Микроскопические системы могут самопроизвольно выходить из состояния равновесия; это явление называют флуктуациями. В статисти-

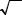
Г л а в а 1. Основы химической термодинамики

ческой физике показано, что относительная величина флуктуаций термодинамических величин имеет порядок 1/ N , где N – число частиц в системе. Если считать, что относительные значения меньше 10–9 невозможно обнаружить экспериментально, то нижний предел для числа частиц в термодинамической системе составляет 1018.

Самопроизвольный переход системы из неравновесного состояния в равновесное называют релаксацией. Основной постулат термодинамики ничего не говорит о времени релаксации, он утверждает, что равновесное состояние системы будет обязательно достигнуто, но длительность такого процесса никак не определена. В классической равновесной тер-

модинамике вообще нет понятия времени.

Для того, чтобы использовать термодинамику для анализа реальных процессов, необходимо выработать некоторые практические критерии, по которым можно было бы судить о завершенности процесса, т.е. достижении равновесного состояния. Состояние системы можно считать равновесным, если текущее значение переменной отличается от равновесного на величину, меньшую, чем ошибка, с которой эта переменная измеряется. Релаксационный процесс можно считать закончившимся, если наблюдаемое свойство системы остается неизменным в течение времени, сопоставимого со временем релаксации по этой переменной. Так как в системе одновременно могут протекать несколько процессов, при рассмотрении условий достижения равновесия надо сопоставлять времена релаксации по разным переменным. Очень часто неравновесная в целом система оказывается равновесной по отношению к процессам с малыми временами релаксации, и их термодинамическое описание оказывается вполне корректным.

Второе исходное положение, или нулевой закон термодинамики описывает свойства систем, находящихся в состоянии теплового равновесия:

Если система А находится в тепловом равновесии с системой В, а та, в свою очередь, находится в равновесии с системой С, то системы А и С также находятся в тепловом равновесии.

Второй постулат говорит о существовании особой интенсивной переменной, характеризующей состояние теплового равновесия и называемой температурой. Системы, находящиеся в тепловом равновесии, имеют одинаковую температуру. Таким образом, нулевой закон – это постулат о существовании температуры. Транзитивностью обладает не только тепловое, но и любое другое равновесие (механическое, диффузионное и т.п.), но в термодинамике постулируется только термическое равновесие, а выравнивание всех остальных интенсивных переменных на контрольной поверхности является следствием этого постулата и второго закона термодинамики.

16	Г л а в а 1. Основы химической термодинамики

Уравнения состояния

(1.1)

(1.2)

(1.3)

Из постулатов термодинамики следует, что при равновесии внутренние переменные термодинамической системы являются функциями внешних переменных и температуры. Например, если система содержит K компонентов, занимает объем V и имеет температуру T, то при равновесии любые термодинамические характеристики этой системы, такие как количества и концентрации образовавшихся соединений, число фаз, давление, теплоемкость, коэффициент термического расширения и другие являются функциями не более, чем (K + 2) независимых переменных. Если же система закрыта, т.е. не может обмениваться веществом с окружением, то для описания ее свойств достаточно двух независимых переменных. Отсюда следует вывод о существовании уравнения состояния термодинамической системы, связывающего внутренние переменные с внешними переменными и температурой или внутренней энергией. В общем случае уравнение состояния имеет вид:

f (a, b,T ) = 0 или a = a(b,T ) ,

где a – совокупность внутренних параметров, b – совокупность внешних параметров, T – температура.

Если внутренним параметром является давление, а внешним – объем, то уравнение состояния

p = p(V , n,T )

называют термическим. Если внутренним параметром является энергия, а внешним – объем, то уравнение состояния

U =U (V , n,T )

называют калорическим.

Количество независимых уравнений состояния равняется вариантности системы, т.е. числу независимых переменных, достаточных для описания термодинамического состояния равновесной системы (оно на единицу больше числа внешних переменных).

В случае закрытой системы в отсутствие внешних полей и поверхностных эффектов число внешних переменных равно 1 (V), соответственно, число уравнений состояния равно 2. Если открытая система содержит K компонентов и может изменять объем, то число внешних переменных составляет K + 1, а число уравнений состояния равно

K + 2.

Если известны термическое и калорическое уравнения состояния, то аппарат термодинамики позволяет определить все термодинамические свойства системы, т.е. получить ее полное термодинамическое описа-

Г л а в а 1. Основы химической термодинамики

ние. Сами уравнения состояния нельзя вывести методами классической

термодинамики, но их можно определить экспериментально.

Самым простым уравнением состояния описывается идеальный газ –

совокупность невзаимодействующих частиц точечного размера:

pV = nRT,

(1.4.а)

где R – универсальная газовая постоянная, или

pVm = RT,

(1.4.б)

где Vm = V/n – мольный объем газа (см. рис. 1.1).

Реальные газы лишь прибли-

женно

описываются

уравнением

состояния идеального газа. При вы-

соких давлениях и низких темпера-

турах (особенно когда газ близок к

конденсации) отклонения от иде-

ального поведения становятся зна-

чительными.

Удобной мерой неидеальности

является

фактор

сжимаемости

Z = pVm/RT, поскольку для идеаль-

ного газа Z = 1 при любых условиях.

На рис. 1.2 представлены факторы

сжимаемости некоторых реальных

газов как функции давления при

Изотермы идеального газа

Рис. 1.1

298 К

(пунктир

соответствует

иде-

22,0.

альному газу). Из рисунка видно,

что

при

высоких

давлениях

для

11,8.

всех

газов Z > 1,

т.е. их труднее

сжать, чем идеальный газ, посколь-

//RTRT

11,6.

ку в этой области преобладают силы

межмолекулярного

отталкивания.

1,4

При низких давлениях для некото-

ZZ==

рых

газов

Z < 1,

что

объясняется

1,2

преобладанием

межмолекулярного

притяжения. При p → 0 эффект

1,0

межмолекулярного

взаимодействия

00,8.

CH4

исчезает, потому что длина свобод-

ного

пробега молекул

становится

200

600

1000

0,600

400

800

много

больше

расстояния

между

p, бар

частицами, и для всех газов Z → 1,

Зависимость фактора

Рис. 1.2

т.е. в этих условиях все газы ведут

сжимаемости некоторых

себя почти идеально.

газов от давления при 298 K

18Г л а в а 1. Основы химической термодинамики

Вотличие от изотерм идеального газа (рис. 1.1), на изотермах реальных газов (рис. 1.3.а) наблюдаются горизонтальные участки, соответствующие процессу конденсации газа в жидкость. Давление, соответствующее горизонтальным участкам, когда жидкость и пар находятся в равновесии, называют давлением насыщенного пара жидкости при данной температуре. При повышении температуры длина

этих участков уменьшается, и при критической температуре Tc на изотерме наблюдается точка перегиба – критическая точка. Она ха-

рактеризуется критической температурой Tc, критическим давлением pc и критическим мольным объемом Vc. Критические константы некоторых газов приведены в приложении (табл. П-2).

а)								б)
120								150
		60oC								1.1 T
100										c
100								100
								100
80		40oC	31.04 oC (Tc)				бар,p			Tc
80		20oC
бар,p		20oC						50		0.9 Tc
										0.9 Tc

60
								1		3		2
40		0oC						0		0.8 Tc
40		0oC								0.8 Tc
20	0.1	0.2	0.3	0.4	0.5	0.6		-50	1	2	5	10
0.0	0.1	0.2	0.3	0.4	0.5	0.6		0.5	1	2	5	10
		V, л моль−1								V, л моль−1

Рис. 1.3	Изотермы CO2: а) экспериментальные;
	б) рассчитанные по уравнению Ван-дер-Ваальса
	б) рассчитанные по уравнению Ван-дер-Ваальса

Для описания реальных газов используют более сложные уравнения состояния, в которых межмолекулярные взаимодействия учитывают с помощью эмпирических параметров, индивидуальных для каждого газа. Некоторые уравнения состояния реальных газов приведены в табл. 1.1. Известно более ста подобных уравнений, отличающихся числом параметров, степенью точности и областью применимости. Выяснилось, что ни одно из уравнений состояния, содержащих менее 5 индивидуальных постоянных, не является достаточно точным для описания реальных газов в широком диапазоне p, V, T, и все эти уравнения оказались непригодными в области конденсации газов. Из простых уравнений с двумя индивидуальными параметрами удовлетворительные результаты дают уравнения Бертло и Дитеричи

(табл. 1.1).

Таблица 1.1

Уравнения состояния реальных газов (для одного моля)

Уравнение

Обычная форма

Приведенная форма

Ван-дер-Ваальса (1873)

p =

−

8Tr

−

= 0.375

V − b

V 2

− 1

27b 2

27bR

V 2

Дитеричи (1898)

Tr e

2− 2/T V

p =

exp −

r r

= 0.271

V − b

RTV

2Vr

− 1

4Rb

Бертло (1900)

8Tr

p =

−

2aR

2 a

= 0.375

V − b

− 1

TV 2

T V

r r

3bR

p = (

)

(

)

Битти-Бриджмена (1927)

1− γ

V + β − α

V 2

где α = a

β = b

−

γ=

Вириальное (1901)

(Камерлинг-Оннес)

p =

...

термодинамики химической Основы .1 а в а л Г

20	Г л а в а 1. Основы химической термодинамики

(1.5.а)

(1.5.б)

(1.6)

Наиболее известным уравнением, описывающим одновременно свойства и газа, и жидкости, является уравнение Ван-дер-Ваальса:

p =

−

Vm − b

Vm2

или

− b +

Vm +

Vm −

= 0

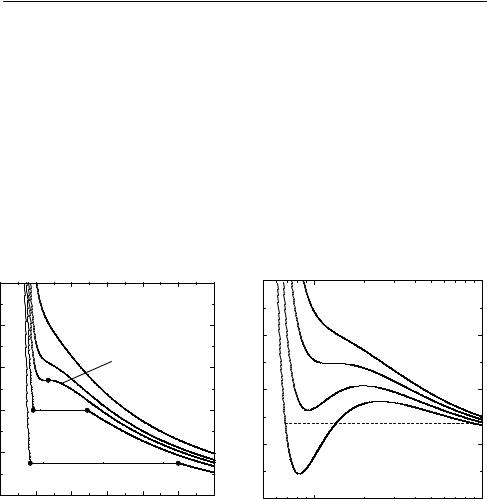
Уравнение (1.5) – кубическое и, следовательно, имеет или три действительных корня, или один действительный и два мнимых. При температурах выше критической уравнение (1.5) имеет один действительный корень, и по мере повышения температуры кривые, вычисленные по уравнению Ван-дер-Ваальса, приближаются к гиперболам, соответствующим уравнению состояния идеального газа (рис. 1.3.б). При температурах ниже критической расчет по уравнению Ван-дер-Ваальса дает волнообразные кривые с тремя действительными корнями, из которых только два (точки 1 и 2) физически осуществимы. Третий корень (точка 3) физически нереален, поскольку находится на участке

кривой, соответствующем условию	∂p	> 0 . Согласно построению


	∂V T

Максвелла для того, чтобы расчетная кривая соответствовала экспериментальной равновесной изотерме, нужно вместо волнообразной кривой провести горизонтальную прямую так, чтобы отсекаемые ею площади под кривой были равны.

В критической точке изотермы реальных газов имеют точку перегиба, координаты которой можно определить из условий

∂p			= 0,

∂V
	T =Tc

∂ 2 p
			= 0.

	2
∂V
		T =T	c

Эти уравнения позволяют связать индивидуальные постоянные уравнения с критическими параметрами газа (см. пример 1-3 и таблицу П-1 в Приложении).

Вводя безразмерные приведенные переменные: давление pr = p/pc, объем Vr = V/Vc и температуру Tr = T/Tc, можно получить приведенное уравнение состояния реального газа, которое не содержит в явном виде индивидуальных постоянных (см. пример 1-3 и таблицу П-1).

Г л а в а 1. Основы химической термодинамики

Состояния разных веществ, имеющие одинаковые значения приведенных переменных, называют соответственными. Согласно закону соответственных состояний, если для рассматриваемых газов значения двух приведенных переменных одинаковы, должны совпадать и значения третьей приведенной переменной. Таким образом, уравнения состояния различных веществ, записанные в приведенных переменных, должны совпадать. Это утверждение эквивалентно постулату о существовании общего универсального приведенного уравнения состояния:

F(pr, Vr, Tr) = 0.

(1.7)

Поскольку

это

уравнение

1.1

не

содержит

явном

виде

= 2.0

индивидуальных

постоянных,

оно должно быть применимо к

0.9

= 1.5

любому газу. Закон соответст-

венных

состояний

является

pV/RT

общим утверждением, не свя-

0.7

занным с

конкретным

видом

T = 1.2

CH4

уравнения состояния. На прак-

Z =

тике

закон

соответственных

0.5

C2H4

состояний

приближенно

вы-

C2H6

Tr = 1.0

C3H8

полняется

для

однотипных

веществ, что позволяет, напри-

0.3

H2O

C4H10

мер, использовать для реаль-

CO2

ных газов обобщенные диа-

0.1

граммы сжимаемости (рис. 1.4).

1.0

2.0

3.0

4.0

5.0

6.0

7.0

0.0

С высокой точностью по-

ведение любого реального газа

Зависимость фактора сжимаемости

Рис. 1.4

можно описать с помощью ви-

риального

уравнения состоя-

некоторых газов от приведенного

давления при разных приведенных

ния – бесконечного ряда по

температурах

степеням обратного объема:

p =

+...

(1.8.а)

или давления

p =

(1+ B2 p

+ B3 p

+...),

(1.8.б)

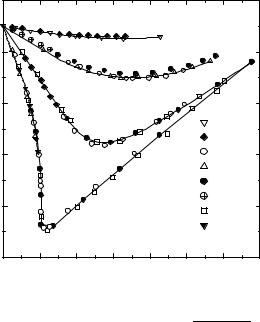
где Bi, Bi' – i-ые вириальные коэффициенты, которые зависят от природы газа и от температуры. Первый вириальный коэффициент равен 1. Так как в большинстве случаев B2/V >> B3 /V 2 >> ..., при описании экспериментальных данных ограничиваются вторым вириальным коэффициентом. При низких температурах B2 < 0, с ростом температуры его

Г л а в а 1. Основы химической термодинамики

значение проходит через ноль, затем становится положительным, дос-

тигает максимума и далее очень медленно убывает. При высоких тем-

пературах B2 и все последующие вириальные коэффициенты стремятся

к нулю (рис. 1.5). Температура, при которой B2 = 0, называется темпе-

ратурой Бойля. При этой температуре фактор сжимаемости реального

газа близок к 1 при любых давлениях. Значения вторых вириальных ко-

эффициентов некоторых газов при разных температурах приведены в

приложении (табл. П-3).

Термическое уравнение со-

стояния

можно

определить

экспериментально,

изучая, на-

пример,

зависимость

объема

CH4

фазы от температуры и давле-

H2O

ния. При этом получают вели-

−1

NH3

чины,

называемые

термиче-

-50

3 моль

скими коэффициентами:

C H

(1.9.а)

∂V

−βV0 ,

, см

3 8

-100

∂p

где β – изотермический коэф-

-150

фициент сжимаемости,

-2000

C2H6

(1.9.б)

(∂∂VT )p

= αV0 ,

200

400

600

800

1000

1200

где α – изобарный коэффици-

T, K

ент расширения, V0 – объем

Зависимость второго вириального

Рис. 1.5

при T = 0 K.

коэффициента некоторых газов

К термическим коэффици-

от температуры

ентам относится также частная

производная

(1.9.в)

∂p

= γp ,

∂T

где γ – изохорный коэффициент давления.

Последнюю величину для конденсированной фазы нельзя измерить

экспериментально, так как невозможно нагреть тело, чтобы не изме-

нился его объем или объем оболочки, в которую оно помещено. Коэф-

фициент γ можно рассчитать, используя цепочечное соотношение Эй-

лера (см. Приложение IV):

(1.10)

откуда

(1.11)

∂p	∂V	∂T	= −1,


∂V T	∂T p	∂p V

γ = βαp .

Г л а в а 1. Основы химической термодинамики

Если известны термические коэффициенты, то уравнение состояния конденсированной фазы можно получить, интегрируя дифференциальное уравнение

	∂V		∂V	dT .	(1.12)
dV =		dp +		dT .	(1.12)
	∂p T		∂T p

Уравнение состояния идеального газа и вириальное уравнение состояния реального газа можно вывести методами статистической термодинамики (см. § 16).

ПРИМЕРЫ

Пример 1-1. Докажите, что при больших объемах уравнение Ван- дер-Ваальса переходит в уравнение идеального газа.

Решение. Уравнение Ван-дер-Ваальса для 1 моля:

p =	RT	−	a	.
	V − b
		V 2

При больших объемах вторым слагаемым в правой части можно пренебречь: a/V 2 → 0. В знаменателе первого слагаемого можно пренебречь постоянной b: V – b → V. В пределе получаем уравнение состояния идеального газа:

V →∞	RT
p →		.
	V

Пример 1-2. Найдите вириальные коэффициенты Bi для газа, подчиняющегося уравнению Ван-дер-Ваальса.

Решение. В уравнении Ван-дер-Ваальса выделим сомножитель RT/V:

p =

−

V − b

V 2

−

RTV

Если разложить первое слагаемое в скобке в ряд по степеням b/V, получим:

	RT			b n		a
p =					−		.
			∑
	V
		n=0		V		RTV

Из этого разложения следует, что второй вириальный коэффициент газа Ван-дер-Ваальса зависит от температуры:

B2 = b − RTa ,

а остальные постоянны: Bn =bn−1 .

<<< < Предыдущая 12 / 482 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в папке 7 семестр

#
02.01.2023721.17 Кб27Лекции.docx
#
02.01.20233.78 Mб28Методичка - Химическая кинетика.pdf
#
02.01.20235.51 Mб75Основы_физич_химии_Теория_и_задачи_Еремин_и_др_2005_480с.pdf