
7 семестр / Основы_физич_химии_Теория_и_задачи_Еремин_и_др_2005_480с
.pdf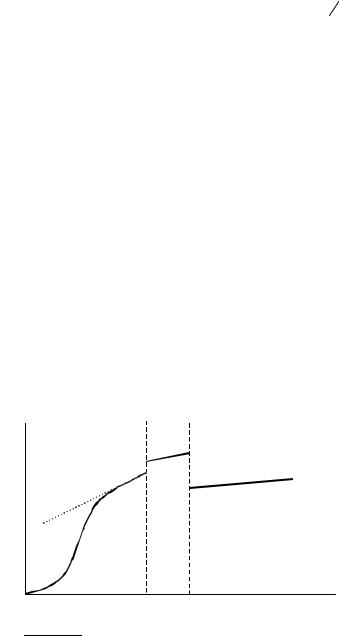
44 |
Г л а в а 1. Основы химической термодинамики |
температуры. В настоящее время нет универсальной формулы, которая позволяла бы получить адекватное описание теплоемкости во всем интервале температур. Поэтому для аппроксимации экспериментальных данных используют различные интерполяционные или экстраполяционные функции. При корректной экстраполяции теплоемкости должны выполняться предельные условия:
при T → ∞ |
lim CV = 3R , |
|
θT →0 |
при T → 0 |
C = aT 3 . |
|
V |
Для слоистых структур (плоских кристаллов) и цепных (волокнистых) структур зависимость CV(T) вблизи абсолютного нуля описывается
степенными функциями вида CV = bT 2 или CV = kT , соответственно.
При невысоких температурах мольная теплоемкость одноатомных идеальных газов равна CV,m = 3/2 R, для двухатомных газов CV,m = 5/2 R. Теплоемкость жидкости обычно несколько превышает теплоемкость твердого тела. Объяснение этих и некоторых других особенностей, присущих теплоемкости, даетсяврамкахстатистической термодинамики(см. § 16).
Интерполяционные формулы позволяют корректно рассчитать значение теплоемкости при любой температуре только внутри указанного температурного интервала. К таким выражениям относятся часто используемые уравнения:
(3.8.а) |
Cp = a + bT, |
|
|
|
|
(3.8.б) |
Cp = a + bT + сТ–2, |
|
|
||
(3.8.в) |
Cp = a + bT + cT lnT. |
|
|
||
Cp |
жидкость |
Число варьируемых па- |
|||
раметров зависит от точно- |
|||||
кристалл |
газ |
||||
сти |
имеющихся данных и |
||||
|
|
ширины |
исследованного |
||
|
|
температурного интервала. |
|||
|
|
Попытка использовать эти |
|||
|
|
уравнения |
как экстраполя- |
||
|
|
ционные, т.е. предсказы- |
|||
|
|
вать |
значения теплоемко- |
||
|
|
сти |
при |
температурах, |
|
|
|
выходящих за пределы ука- |
|||
|
T, K |
занного |
температурного |
||
|
интервала часто приводит к |
||||
Рис. 3.3 |
Температурная зависимость |
физически |
некорректным |
||
|
теплоемкости вещества |
величинам CV или Cp. Это |
|||

Г л а в а 1. Основы химической термодинамики |
45 |
утверждение продемонстрировано на рис. 3.3 (пунктирная линия), где приведен график зависимости Cp(T) некоторого вещества в различных агрегатных состояниях.
При отсутствии экспериментальных данных о теплоемкостях веществ обычно используют различные способы оценок этих величин:
•правило Дюлонга–Пти: теплоемкость CV твердых соединений приблизительно равна сумме атомных теплоемкостей; при этом при-
нимают, что для простых веществ они одинаковы и равны
25 Дж моль–1К–1 ≈ 3R (исключение составляют легкие элементы);
•правило Неймана–Коппа (правило аддитивности): теплоемкость Cp сложного вещества равна сумме теплоемкостей образующих соединение простых веществ;
•мольные теплоемкости органических жидкостей рассчитывают суммированием атомно-групповых составляющих (инкрементов) теплоемкостей. Значения некоторых инкрементов приведены в табл. 3.2;
•для большинства органических соединений в небольшом интервале
температур Cp = a + bT, причем b/a = 0.0022.
Так как с изменением давления энтальпия идеального газа не изме-
няется, то и энтальпия реакции между идеальными газами от давления |
|||||||||
не зависит. В случае реальных газов отличие ∆rH от соответствующей |
|||||||||
величины, полученной для идеальных газов, можно вычислить, напри- |
|||||||||
мер, с помощью уравнений состояния участников реакции1: |
|
||||||||
|
|
∂∆ r H |
|
= −T |
|
∂∆ rV |
+ ∆ V . |
(3.9) |
|
|
|
∂p |
|
|
|
|
|
r |
|
|
|
T |
|
|
∂T p |
|
|
||
Для конденсированной фазы зависимость энтальпии реакции от |
|||||||||
давления учитывают с помощью изобарного коэффициента расширения |
|||||||||
вещества α (см. § 1). |
|
|
|
|
|
|
|
|
|
Значения некоторых групповых вкладов |
Таблица 3.2 |
||||||||
изобарных теплоемкостей (T = 293 K) |
|
||||||||
Атом или группа |
Cp, Дж моль–1 К–1 |
|
Атом или группа Cp, Дж моль–1 К–1 |
||||||
–CH3 |
|
41.32 |
|
|
|
–O– |
|
35.02 |
|
–СH2– |
|
26.45 |
|
|
–NH2 |
O |
63.6 |
||
–CN |
|
58.16 |
|
|
|
C |
79.90 |
||
|
|
|
|
OH |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
O |
|
–С6H5 |
|
127.61 |
|
|
|
_ |
60.75 |
||
|
|
|
|
|
|
|
|
O |
|
–CH= |
|
22.69 |
|
|
|
C |
O |
61.5 |
|
|
|
|
|
|
|||||
1 Вывод формулы (3.9) приведен в § 5. |
|
|
|
||||||

46 |
Г л а в а 1. Основы химической термодинамики |
ПРИМЕРЫ
Пример 3-1. Стандартные энтальпии образования жидкой и газообразной воды при 298 К равны –285.8 и –241.8 кДж моль–1 соответственно. Рассчитайте энтальпию испарения воды при этой температуре.
Решение. Энтальпии образования соответствуют следующим реакциям:
H2(г) + 12 O2(г) = H2O(ж), ∆H1° = –285.8 кДж моль–1;
H2(г) + 12 O2(г) = H2O(г), ∆H2° = –241.8 кДж моль–1.
Вторую реакцию можно провести в две стадии: сначала сжечь водород с образованием жидкой воды по первой реакции, а затем испарить воду:
H2O(ж) = H2O(г), ∆испH° = ?
Тогда, согласно закону Гесса,
∆H1° + ∆испH° = ∆H2°,
откуда
∆испH° = –241.8 – (–285.8) = 44.0 кДж моль–1
Ответ. 44.0 кДж моль–1.
Пример 3-2. Рассчитайте энтальпию реакции
6C(г) + 6H(г) = C6H6(г)
а) по энтальпиям образования; б) по энергиям связи, в предположении, что двойные связи в моле-
куле C6H6 фиксированы.
Решение. а) Энтальпии образования (в кДж моль–1) находим в Приложении (табл. П-5, П-6):
∆fH °(C6H6(г)) = 82.93, ∆fH °(C(г)) = 716.68, ∆fH °(H(г)) = 217.97.
Энтальпия реакции равна:
∆rH ° = 82.93 – 6 716.68 – 6 217.97 = –5525 кДж моль–1.
б) В данной реакции химические связи не разрываются, а только образуются. В приближении фиксированных двойных связей молекула C6H6 содержит 6 связей C−H, 3 связи C−C и 3 связи C=C. Энергии связей (в кДж моль–1) (Приложение, табл. П-4):
E(C−H) = 412, E(C−C) = 348, E(C=C) = 612.
Энтальпия реакции равна:
∆rH ° = –(6 412 + 3 348 + 3 612) = –5352 кДж моль–1.
Г л а в а 1. Основы химической термодинамики |
47 |
Разница с точным результатом –5525 кДж моль–1 обусловлена тем, что в молекуле бензола нет одинарных связей C−C и двойных связей C=C, а есть 6 ароматических связей C C.
Ответ. а) –5525 кДж моль–1; б) –5352 кДж моль–1.
Пример 3-3. Пользуясь справочными данными, рассчитайте энтальпию реакции
3Cu(тв) + 8HNO3(aq) = 3Cu(NO3)2(aq) + 2NO(г) + 4H2O(ж)
при 298 К.
Решение. Сокращенное ионное уравнение реакции имеет вид:
3Cu(тв) + 8H+(aq) + 2NO3–(aq) = 3Cu2+(aq) + 2NO(г) + 4H2O(ж).
По закону Гесса, энтальпия реакции равна:
∆rH° = 4∆fH°(H2O(ж)) + 2∆fH°(NO(г)) + 3∆fH°(Cu2+(aq)) – 2∆fH°(NO3–(aq))
(энтальпии образования меди и иона H+ равны, по определению, 0). Подставляя значения энтальпий образования (Приложение, табл. П-5), находим:
∆rH ° = 4 (–285.8) + 2 90.25 + 3 64.77 – 2 (–205.0) = –358.4 кДж
(в расчете на три моля меди).
Ответ. –358.4 кДж.
Пример 3-4. Рассчитайте энтальпию сгорания метана при 1000 К, если даны энтальпии образования при 298 К:
∆fH °(CH4) = –17.9 ккал моль–1, ∆fH °(CO2) = –94.1 ккал моль–1, ∆fH °(H2O(г)) = –57.8 ккал моль–1.
Теплоемкости газов (в кал моль–1К–1) в интервале от 298 до 1000 К равны:
Cp(CH4) = 3.422 + 0.0178 T, Cp(O2) = 6.095 + 0.0033 T, Cp(CO2) = 6.396 + 0.0102 T, Cp(H2O(г)) = 7.188 + 0.0024 T.
Решение. Энтальпия реакции сгорания метана
CH4(г) + 2O2(г) = CO2(г) + 2H2O(г)
при298 Кравна:
∆r H298o = –94.1 + 2 (–57.8) – (–17.9) = –191.8 ккал моль–1.
Найдем разность теплоемкостей как функцию температуры:
∆Cp = Cp(CO2) + 2Cp(H2O(г)) – Cp(CH4) – 2Cp(O2) = = 5.16 – 0.0094T (кал моль–1К–1).

48 |
Г л а в а 1. Основы химической термодинамики |
Энтальпию реакции при 1000 К рассчитаем по уравнению Кирхгофа:
|
|
1000 |
∆r H1000o |
= ∆r H 298o |
+ ∫ (5.16 − 0.0094 T )dT = |
|
|
298 |
=–191800 + 5.16 (1000 – 298) – 0.0094 (10002 – 2982)/2 = –192500 кал моль–1.
Ответ. –192.5 ккал моль–1.
Пример 3-5. Используя инкрементную схему, рассчитайте значение изобарной теплоемкости изобутилацетата при 293 К.
Решение. Исходя из структурных данных и величин атомногрупповых вкладов, приведенных в табл. 3.2:
Cp = 3Cp(–CH3) + Cp(–COO–) + Cp(–CH2–) + Cp(–CH=) = = 3 41.32 + 60.75 + 26.45 + 22.69 = 233.85 Дж моль–1К–1.
Опытноезначение222.88 Дж моль–1К–1, т.е. ошибканепревышает5%. Ответ. 233.85 Дж моль–1К–1.
ЗАДАЧИ
3-1. Сколько тепла потребуется на перевод 500 г Al (т.пл. 658 °С, ∆плH° = 92.4 кал г–1), взятого при 25 °С, в расплавленное состояние, ес-
ли Cp(Al(тв)) = 0.183 + 1.096 10–4T кал г–1К–1?
3-2. Стандартная энтальпия реакции
CaCO3(тв) = CaO(тв) + CO2(г),
протекающей в открытом сосуде при температуре 1000 К, равна 169 кДж моль–1. Чему равна теплота этой реакции, протекающей при той же температуре, но в закрытом сосуде?
3-3. Рассчитайте стандартную внутреннюю энергию образования жидкого бензола при 298 К, если стандартная энтальпия его образования равна 49.0 кДж моль–1.
3-4. Рассчитайте энтальпию образования N2O5(г) при T = 298 К на основании следующих данных:
2NO(г) + O2(г) = 2NO2(г), |
∆H1° = –114.2 кДж моль–1, |
4NO2(г) + O2(г) = 2N2O5(г), |
∆H2° = –110.2 кДж моль–1, |
N2(г) + O2(г) = 2NO(г), |
∆H3° = 182.6 кДж моль–1. |
3-5. Энтальпии сгорания α-глюкозы, β-фруктозы и сахарозы при 25 °С равны –2802, –2810 и –5644 кДж моль–1 соответственно. Рассчитайте энтальпию гидролиза сахарозы.
Г л а в а 1. Основы химической термодинамики |
49 |
3-6. Определите энтальпию образования диборана B2H6(г) при T = 298 К из следующих данных:
B2H6(г) + 3O2(г) = B2O3(тв) + 3H2O(г), |
∆H1° = –2035.6 кДж моль–1, |
2B(тв) + 3/2 O2(г) = B2O3(тв), |
∆H2° = –1273.5 кДж моль–1, |
H2(г) + 1/2 O2(г) = H2O(г), |
∆H3° = –241.8 кДж моль–1. |
3-7. Рассчитайте энтальпию образования сульфата цинка из простых веществ при T = 298 К на основании следующих данных:
ZnS = Zn + S, |
∆H1° = 200.5 кДж моль–1, |
2ZnS + 3O2 = 2ZnO + 2SO2, |
∆H2° = –893.5 кДж моль–1, |
2SO2 + O2 = 2SO3, |
∆H3° = –198.2 кДж моль–1, |
ZnSO4 = ZnO + SO3, |
∆H4° = 235.0 кДж моль–1. |
3-8. Найдите ∆rH°298 для реакции |
|
CH4 + Cl2 = CH3Cl(г) + HCl(г),
если известны теплоты сгорания:
метана (∆cH°(CH4) = –890.6 кДж моль–1),
хлорметана (∆cH°(CH3Cl) = –689.8 кДж моль–1), водорода (∆cH°(H2) = –285.8 кДж моль–1)
и теплота образования HCl (∆fH°(HCl) = –92.3 кДж моль–1).
3-9. Рассчитайте тепловой эффект реакции
NH3 + 5/4 O2 = NO + 3/2 H2O(г)
при T = 298 K, если известны следующие данные:
H2O(г) = H2O(ж), |
∆H1° = –44 кДж моль–1, |
1/2N2 + 3/2H2 = NH3, |
∆H2° = –46.2 кДж моль–1, |
H2 + 1/2O2 = H2O(ж), |
∆H3° = –285.8 кДж моль–1, |
NO = 1/2N2 + 1/2O2, |
∆H4° = –91.3 кДж моль–1. |
3-10. |
При взаимодействии 10 г металлического натрия |
с водой |
∆rH298 |
= –79.91 кДж, а при взаимодействии 20 г оксида натрия с водой |
|
∆rH298 |
= –76.76 кДж. Вода берется в большом избытке. Рассчитайте теп- |
|
лоту образования оксида натрия ∆f H 298o (Na2O), если ∆f H 298o |
(H2O(ж)) = |
|
= –285.8 кДж моль–1.
3-11. Энергия связи в молекуле H2 равна 432.1 кДж моль–1, а энергия связи в молекуле N2 равна 945.3 кДж моль–1. Какова энтальпия атомизации аммиака, если энтальпия образования аммиака равна –46.2 кДж моль–1?
3-12. Рассчитайте стандартный тепловой эффект реакции нейтрализации
NaOH + HCl = NaCl + H2O,
протекающей в водном растворе при 298 К.

50 |
Г л а в а 1. Основы химической термодинамики |
3-13. Рассчитайте стандартный тепловой эффект реакции
CaSO4(тв) + Na2CO3(aq) = CaCO3(тв) + Na2SO4(aq)
при 298 К, если ∆f H 298o (CaSO4(тв)) = –1434 кДж моль–1.
3-14. Напишите уравнение Кирхгофа для реакции, протекающей при постоянном объеме.
3-15. Зависимость теплового эффекта реакции
CH3OH(г) + 3/2O2 = CO2 + 2H2O(г)
от температуры выражается уравнением:
∆r HTo(Дж) = −684.7 103 + 36.77T − 38.56 10−3T 2 +
+8.21 10−6 T 3 + 2.88 105 / T .
Рассчитайтеизменение теплоемкости∆Cp дляэтойреакциипри500 К.
3-16. Стандартная энтальпия образования Al2O3(тв) при 298 К равна –1675 кДж моль–1. Рассчитайте стандартную энтальпию образования
Al2O3(тв) при 800 К, если даны мольные теплоемкости (в Дж моль–1 К–1):
Cp(Al) = 20.67 + 12.39 10–3T,
Cp(O2) = 31.46 + 3.39 10–3T – 3.77 105T –2, Cp(Al2O3) = 114.56 + 12.89 10–3T – 34.31 105T –2.
3-17. Энтальпия диссоциации карбоната кальция при 900 °С и давлении 1 атм равна 178 кДж моль–1. Выведите уравнение зависимости энтальпии реакции от температуры и рассчитайте количество теплоты, поглощенное при разложении 1 кг карбоната кальция при 1000 °С и 1 атм,
если даны мольные теплоемкости (в Дж моль–1 К–1):
Cp(СaCO3(тв)) = 104.5 + 21.92 10–3T – 25.94 105T –2, Cp(СaO(тв)) = 49.63 + 4.52 10–3T – 6.95 105T –2, Cp(CO2(г)) = 44.14 + 9.04 10–3T – 8.53 105T –2.
3-18. Зависимость теплового эффекта реакции
1
H2(г) + 2 O2(г) = H2O(г)
от температуры выражается уравнением:
∆ r HTo(Дж моль–1) = −237.65 103 − 13.01T + 2.88 10−3 T 2 − 1.71 105 / T .
Рассчитайте изменение теплоемкости ∆Cp и ∆CV для этой реакции при 800 К.
3-19. Рассчитайте тепловой эффект образования гексагидрата нитрата магния Mg(NO3)2 6H2O(тв), если известны следующие данные:

Г л а в а 1. Основы химической термодинамики |
51 |
Mg(тв) + 2H+(aq) → Mg2+(aq) + H2(г) – 465.8 кДж
H2(г) + N2(г) + 3O2(г) → 2H+(aq) + 2NO3–(aq) – 409.4 кДж
Mg(NO3)26H2O(тв) → Mg2+(aq) + 2NO3–(aq) + 6H2O(ж) + 21.3 кДж
H2(г) + 12 O2(г) = H2O(ж) – 285.8 кДж.
3-20. Известны тепловые эффекты следующих реакций:
CH3COOC2H5(ж) + OH–(aq) = CH3COO–(aq) + C2H5OH(ж)
∆ r H 298o = –54.7 кДж моль–1;
CH3COOH(ж) + OH–(aq) = CH3COO–(aq) + H2O(ж)
∆ r H 298o = –57.3 кДж моль–1;
СH3COOC2H5(ж) + 2H2(г) = 2C2H5OH(ж)
∆ r H 298o = –76.4 кДж моль–1.
Рассчитайте тепловой эффект реакции:
C2H5OH(ж) + O2(г) = CH3COOH(ж) + H2O(ж),
если энтальпия образования жидкой воды равна –285.8 кДж моль–1.
3-21. Известны тепловые эффекты следующих реакций:
C2H6(г) = 2CH3(г), |
∆ r H 298o |
= 376.1 кДж моль–1 |
|
CH3Cl(г) + Cl(г) = CH3(г) + Cl2(г), |
∆ r H 298o |
= 106.0 кДж моль–1 |
|
2CH3Cl(г) + 2Na(тв) = C2H6(г) + 2NaCl(тв), ∆ r H 298o |
= –742.9 кДжмоль–1 |
||
Рассчитайте энергию связи в молекуле Cl2, если энтальпия образо- |
|||
вания хлорида натрия равна –411.1 кДж моль–1. |
|
|
|
3-22. Известны тепловые эффекты следующих реакций: |
|||
CH3(г) + H(г)= CH4(г), |
∆ r H 298o |
= –438.5 кДж моль–1 |
|
CH3Br(г) + Br(г) = CH3(г) + Br2(ж), |
∆ r H 298o |
= 45.5 кДж моль–1 |
|
CH3Br(ж) = CH3Br(г), |
∆ r H 298o |
= 23.9 кДж моль–1 |
|
Рассчитайте энтальпию реакции |
|
|
|
CH4(г) + Br2(ж) = CH3Br(ж) + HBr(г),
если энергия связи в молекуле HBr равна 366.3 кДж моль–1.
3-23. Известны тепловые эффекты следующих реакций:
C2H2(г) = 2C(гр) + H2(г), |
∆ r H 298o |
= –226.7 кДж моль–1 |
3C2H2(г) = C6H6(ж), |
∆ r H 298o |
= –631.1 кДж моль–1 |
C6H6(ж) = C6H6(г), |
∆ r H 298o |
= 33.9 кДж моль–1 |

52 |
Г л а в а 1. Основы химической термодинамики |
Рассчитайте энтальпию разложения молекулы бензола на атомы в газовой фазе, если энергия связи в молекуле H2 равна 436.0 кДж моль–1, а энтальпия испарения графита составляет 716.7 кДж моль–1.
3-24. Стандартная энтальпия образования метиламина при 25 °С равна –23.0 кДж моль–1. Рассчитайте стандартную энтальпию образования метиламина при 150 °С, если известны теплоемкости:
Вещество |
C(графит) |
H2(г) |
N2(г) |
CH5N(г) |
|
|
|
|
|
Cp, Дж моль–1 К–1 |
8.53 |
28.82 |
29.13 |
53.10 |
3-25. Стандартная энтальпия образования формальдегида при 25 °С равна –108.6 кДж моль–1. Рассчитайте стандартную энтальпию образования формальдегида при 150 °С, если известны теплоемкости:
Вещество C(графит)
Cp, Дж моль–1 К–1 8.53
H2(г) |
O2(г) |
CH2O(г) |
|
|
|
28.82 |
29.36 |
35.40 |
|
|
|
3-26. Используя значения энтальпий некоторых окислительно-вос- становительных реакций с участием природных кофакторов (T = 298 K, фосфатный буфер, pH = 8), рассчитайте энтальпии реакций никотинамидадениндинуклеотида (НАД+) с различными восстановленными формами флавинмононуклеотида:
ФМН-Н2 + НАД+ = ФМН + НАД-Н + Н+ 2 ФМН-Н2 + НАД+ = (ФМН-Н)2 + НАД-Н + Н+
Реакция |
∆rH °, кДж моль–1 |
НАД+ + Н2 = НАД-Н + Н+ |
–27.9 |
2Fe(CN)63– + ФМН-Н2 = 2Fe(CN)64– + ФМН + 2Н+ |
–164.0 |
Fe(CN)63– + ФМН-Н2 = Fe(CN)64– + 1/2(ФМН-H)2 + Н+ |
–98.7 |
Fe(CN)63– + 1/2Н2 = Fe(CN)64– + Н+ |
–110.9 |
3-27. Используя данные таблицы, рассчитайте энтальпии реакций превращения α,β-D-маннозы в α,β-D-фруктозу и α-лактозы в β-мальтозу (водный раствор, 298.15 К).
Реакция |
∆rH °, кДж моль–1 |
α,β-D-глюкоза = α,β-D-манноза |
9.3 |
α,β-D-глюкоза = α,β-D-фруктоза |
9.3 |
α-мальтоза = β-мальтоза |
–0.5 |
α-лактоза = α-мальтоза |
–5.9 |

Г л а в а 1. Основы химической термодинамики |
53 |
3-28. На рисунках представлены графики зависимостей ∆rC p = f(T). Изобразите соответствующие зависимости ∆rH = f(T).
|
|
(a) |
(б) |
|
(в) |
||
∆rC p |
|
|
∆rC p |
|
∆rC p |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T T T
§ 4. Второй закон термодинамики. Энтропия
Первый закон термодинамики определяет энергетический баланс различных процессов, в том числе химических реакций. Второй закон позволяет предсказать, при каких условиях процесс возможен и каким будет его результат при заданных условиях. Существуют несколько эквивалентных формулировок этого закона; для практического использования удобна следующая:
Существует экстенсивная функция состояния термодинамической системы – энтропия (S). При протекании в изолированной системе обратимых процессов эта функция остается неизменной, а при необратимых – увеличивается
dSU,V, n ≥ 01. |
(4.1) |
Из этого следует, что после завершения релаксационных процессов при состоянии термодинамического равновесия энтропия изолированной системы достигает своего максимума:
dSU,V,n = 0, |
d 2S < 0. |
Размерность энтропии – [энергия/температура = Дж К–1], в справочных изданиях приводятся мольные величины [Дж моль–1 К–1].
Понятие энтропии было введено в термодинамику Р. Клаузиусом. Неравенство Клаузиуса связывает изменение энтропии с количеством
1 n = (n1, …, nN) – набор количеств веществ.
