3832

Поскольку система имеет одну неколебательную степень свободы, которая несу-

щественна, можно записать дифференциальное уравнение, описывающее поведение этой электромеханической системы, в виде

реактивной и корпусной частей; x1, x2 – координаты реактивной и корпусной частей, от-

считываемые от положения равновесия; x=x2-x1 – относительная координата; b –

коэффициент сопротивления демпфера; с – коэффициент жесткости пружины; i – сила то-

ка; L – индуктивность обмотки; R – электрическое сопротивление обмотки; u – напряже-

ние, подводимое к обмотке: F – электромагнитная сила притяжения.

В положении статического равновесия x=0. Сила притяжения электромагнита F

= W/ x, где W 1 Li2 – потенциальная энергия магнитного поля. Индуктивность обмот-

2

ки при переменном воздушном зазоре магнитопровода может быть аппроксимирована вы-

ражением

где – коэффициент, учитывающий рассеяние магнитного потока; x0 – начальный воз-

душный зазор. Тогда

Получена система нелинейных параметрических уравнений, которую для анализа и синтеза систем автоматического управления целесообразно линеаризовать. Здесь возмож-

ны два подхода. Во-первых, можно рассматривать систему в виде звена «вход-выход» без

измерения и управления промежуточными координатами, в частности, током вибровозбу-

81

дителя. В этом случае достаточно линеаризовать, например методом малых отклонений,

систему (2.17). Во-вторых, система может быть структурирована в соответствии с коорди-

натами «вход-выход» отдельных, образующих ее элементов и в этом случае модель пре-

доставляет возможность управлять промежуточными координатами, что, в ряде случаев,

предпочтительней.

В первом случае, рассматривая малые отклонения переменных , , u от их значений 0, 0, u0 в установившемся режиме, из (2.17), отбрасывая величины высших по-

рядков малости, имеем

ханической связи (внутренней обратной связи).

В установившемся режиме 0 =1, 0 =i/2.

Для получения соответствующих второму случаю дифференциальных уравнений разложим нелинейности (2.15) и (2.16) в ряд Тейлора, удерживая только линейные члены разложения. Тогда

ференцирования гибкой внутренней обратной связи. Обозначив bT1 , первое уравне-

2m

ние системы (2.21) можно записать в форме, соответствующей первому уравнению систе-

мы (2.18).

В заключение необходимо заметить, что определение динамических свойств объектов с помощью дифференциальных уравнений может быть по-

ка успешно выполнено только для сравнительно простых объектов. Как пра-

вило, в редких случаях можно при небольшой затрате времени составить достаточно точное дифференциальное уравнение объекта.

2.2.2. Передаточные функции объектов и элементов

систем автоматического управления с сосредоточенными параметрами

Рассмотрим общий случай неоднородного дифференциального уравне-

ния

где коэффициенты ai и bj (i=0,1,…,n; j=0,1,…, m) могут быть функциями вре-

мени.

Обозначая через D оператор дифференцирования по времени, т.е.:

выходную переменную в (2.22) можно представить в виде:

83

является дробно-рациональной функцией от оператора дифференцирования

D и называется передаточной функцией эвена или системы. Таким образом,

передаточная функция устанавливает зависимость выходной переменной y от входной переменной x в операторной форме:

соответствующей (1.1), т.е. определяющей оператор системы.

Преобразование (2.23) или D-преобразование, и полученное с его по-

мощью уравнение (2.24) или (2.26), несмотря на некоторую формальность процедуры, имеет в своей основе прямое преобразование Лапласа, обозна-

чаемое L[ ], и широко используемое в теории автоматического управления для упрощения расчетов и проектирования систем. Для этой цели каждой функции времени t, входящей в дифференциальное уравнение, сопоставляет-

ся функция другого переменного s = с+j. Чтобы подчеркнуть соответствие изображения F(s) своему оригиналу f(t), для их обозначения обычно выби-

рают одинаковые буквы (для изображения - заглавные), а также применяют значок в виде стрелки:

f (t ) F( s ).

При этом уравнения динамики записывают не через оригиналы функ-

ций f(t), а в виде изображений функций F(s), получаемых с помощью инте-

грала вида:

Преобразование (2.27) или прямое преобразование Лапласа, справедли-

84

во для кусочно-непрерывных функций, определенных при t>0 и принимае-

мых равными нулю при t<0.

Покажем соответствие преобразований (2.23) и (2.27) для чего опреде-

лим преобразование по Лапласу производной функции f(t). В соответствии с

(2.27) имеем:

Таким образом, дифференцированию оригинала соответствуют умно-

жение изображения на s и вычитание начального значения f(0).

Аналогичным образом легко показать, что интегрированию оригинала соответствует деление изображения на s:

Применяя (2.28) к (2.22) при нулевых начальных условиях, получим:

где A(s) и B(s) полиномы числителя и знаменателя передаточной функции.

Нетрудно видеть, что если в (2.25) заменить оператор дифференциро-

вания D на s то в результате будет получено выражение (2.30), называемое

передаточной функцией, под которой понимается отношение изображе-

ния выходной величины для объекта или устройства системы к изображе-

нию функции входной величины, полученных при нулевых начальных условиях

/8/.

Если входное воздействие представлено -функцией x(t)= (t), изобра-

жение Лапласа которой L[ (t)]=1, то из (2.30) следует, что изображение вы-

ходного сигнала y(t) = (t), где (t) – импульсная переходная функция систе-

мы (см. 2.3.2), есть передаточная функция звена или системы. Действитель-

85

но, в соответствии с (2.30) можно записать:

Таким образом, передаточная функция есть преобразованная по Лап-

ласу импульсная переходная функция звена или системы, т.е реакция звена или системы на импульсное входное воздействие.

Анализ (2.30) показывает, что применение преобразования Лапласа к

(2.22) позволяет перейти от дифференциальных уравнений для оригиналов к алгебраическим уравнениям для их изображений. После решения алгебраи-

ческих уравнений с помощью обратного преобразования Лапласа L-1[ ]

осуществляется переход от изображений к оригиналам. Под с в (2.32) пони-

мается абсцисса абсолютной сходимости, т.е. минимальное положительное значение параметра c при котором выполняется условие

В соответствии с изложенным, уравнения (2.18) и (2.21) можно запи-

сать в виде

T12s2 2 T1s 1 (s ) Kk (s ),

(2.33)

Tm s 1 (s ) u(s ) Koc (s )

и

Соответствующие (2.33) и (2.34) динамические структуры объекта управления показаны на рис. 2.6.

Несмотря на внешнее сходство приведенных структурных схем, они

86

принципиально по-разному отражают динамические процессы в системе.

Объясняется это тем, что во втором случае изначально рассматривалась мо-

дель с раскрытой структурой /7/ причинно-следственных связей, учитываю-

щей динамические режимы двух элементов расчетной схемы: механической колебательной системы и электромагнитного вибровозбудителя, выходной величиной которого при-

а – в первом, б – во втором расчетном случае

и установившееся откло-

нение тока определяется только отклонением питающего напряжения;

во-вторых, что наиболее важно, полученные линеаризованные зависи-

мости свидетельствуют о непостоянстве жесткости системы, которая опреде-

ляется не только коэффициентом жесткости пружины, но зависит также и от электрических параметров системы. Если учесть, что величину тока i0 можно изменять подмагничиванием, то можно сделать вывод о возможности незна-

чительного параметрического управления системой для обеспечения, напри-

мер, резонансного режима при изменяющихся параметрах нагрузки.

В заключение определим некоторые термины, используемые в связи с передаточными функциями.

1. Корни уравнения В(s) =0 называются нулями системы. 87

2.Корни уравнения А(s) = 0 называются полюсами системы.

3.Если уравнение А(s) = 0 имеет nk корней при s = k, то говорят, что полюс k имеет кратность nk.

4.Различие в степенях полиномов А(s) и В(s) называется относитель-

ной степенью.

5. Если т < п, то модель строго собственная. Это означает, что относи-

тельная степень положительна.

6. Если т = п, то модель бисобственная. Это означает, что относитель-

ная степень нулевая.

7.Если т ≤ п, то модель собственная.

8.Если т > п, то модель несобственная (или имеет отрицательную от-

носительную степень).

Реальные системы почти всегда строго собственные. Однако некоторые методы проектирования регуляторов приводят к бисобственным или даже к несобственным передаточным функциям. Чтобы быть реализуемыми, эти ре-

гуляторы обычно делаются бисобственными, например, дополняя А(s) со-

множителями типа ( is+1).

2.2.3. Передаточные функции объектов и элементов

систем автоматического управления с распределенными параметрами

Всовременных системах автоматического управления отдельные блоки

иагрегаты часто располагаются на значительных расстояниях друг от друга.

Для соединения элементов в единую систему широко применяются линии передачи сигналов чаще всего в виде двухпроводных или однопроводных линий, экранированных кабелей, фидеров и волноводов. У подобных элемен-

тов основные электрические характеристики - сопротивление, емкость, ин-

дуктивность - не сосредоточены в каких-то отдельных частях, а распределе-

ны непрерывно вдоль линии. Протяженность таких линий соизмерима с дли-

ной рабочей электромагнитной волны или значительно ее превосходит. Та88

кие элементы обычно называются элементами с распределенными парамет-

рами.

Поскольку длина электромагнитной волны обратно пропорциональна ее частоте (Гц), то, например, уже в диапазоне частот (3 102 - 3 104) МГц длинной можно считать линию, длина которой больше (1,0 – 0,01) м соответ-

ственно. Таким образом, строго говоря, почти все реальные элементы, вхо-

дящие в состав систем автоматического управления, также представляют со-

бою элементы с распределенными параметрами. Но в подавляющем боль-

шинстве случаев реальный элемент можно с достаточной степенью точности заменить упрощенной моделью - системой с сосредоточенными параметрами и идеальными линиями связи, в которых отсутствуют потери энергии и за-

паздывание при прохождении сигналов. Такая замена дает возможность оп-

ределить динамические характеристики элемента с достаточной точностью лишь в том случае, когда эквивалентное сопротивление всех линий связи достаточно мало по сравнению с эквивалентным сопротивлением соединяе-

мых ими деталей. При этом процессы изменения токов и напряжений в цепи теряют «волновой» характер и становятся чисто «колебательными», анализ их базируется на решении дифференциальных уравнений в полных произ-

водных /23/. Если же волновой характер процессов представляет основу по-

лезных функций цепи, либо существенно влияет на характеристики переда-

ваемого сигнала, соответствующую линию связи необходимо считать длин-

ной линией с распределенными (рассредоточенными) параметрами. Их ана-

лиз базируется на основе решений дифференциальных уравнений в частных производных.

Проводные линии связи, вне зависимости от их технической реализа-

ции описываются одними и теми же уравнениями. Рассматривая процессы в длинной линии с потерями, будем характеризовать ее /4/ следующими рас-

пределенными по длине параметрами: активным сопротивлением R, индук-

тивностью L, емкостью С и активной проводимостью G между проводами

89

линии, обусловленной наличием определенного конечного омического со-

противления их изоляции и промежутка между ними. В общем случае эти параметры могут быть распределены по длине линии неравномерно. Такие линии называются неоднородными. Если перечисленные параметры распре-

делены вдоль линии равномерно, то линия называется однородной. На прак-

тике в подавляющем большинстве случаев применяются только однородные длинные линии.

Напряжение и ток в каждом сечении однородной линии будут функ-

циями времени t и координаты сечения х: u = u(t,x), i = i(t,x). Условимся счи-

тать, что началу линии соответствует x=0, а концу – х = l, где l - полная длина

линии.

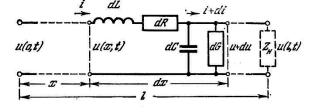
Для составления системы дифференциальных уравнений, описываю-

щих длинную линию, представим ее бесконечно малый отрезок длины dx уп-

рощенной моделью, изображенной на рис. 2.7.

Изменение тока, протекающего в линии между теми же сечениями, вы-

зывается утечкой тока через проводимость Gudx и током заряда емкости

90