
3832
.pdf
его коэффициенты имели один и тот же знак (или все положительны, или все отрицательны). Выразим полином (3.158) в форме
a0 ( 1 )( 2 ) ( n ) 0 |
(3.162) |
Из алгебры известно, что корни полинома с действительными коэффи-
циентами или действительны, или являются попарно сопряженными ком-
плексными величинами. Для отрицательного действительного корня r = -
и, следовательно, - r = + .
Для двух комплексных сопряженных корней с отрицательными дейст-
вительными частями r = - +j , r+1 = - -j и
( r )( r 1 ) [ ( j )][ ( j )] 2 2 2 2
Таким образом, полином (3.158) является произведением линейных
двучленов и квадратных трехчленов с положительными коэффициентами.
|
|
|
|
|
Im |
Отсюда следует, что все коэффициенты полино- |
|
|
|
1 |
ма положительны, что и требовалось доказать. |
||||
|
|
|
|||||
3 |
|
|
|||||
|
|
|
|
Если все корни уравнения (3.158) имеют |
|||
|
6 |
|
|
||||
|
|
|
|
||||
|
|
|
|||||
|
|
|
5 |
Re |
отрицательные вещественные части (см. рис. |
||
|
|
|
|
||||
4 |
|
3.24), то нулевое решение системы (2.257) и по- |
|||||
|
|
|
2 |
|
|||
|
|
|
|
ведение соответствующей ей системы автомати- |
|||
|
|
|
|
|
|
||
Рис. 3.24. Расположение |
|||||||
|
|||||||
корней характеристического |
ческого управления асимптотически устойчиво. |
||||||
уравнения для асимптотиче- |
Если среди корней уравнения (3.158) есть |
||||||
ски устойчивой системы |
|||||||
хотя бы один с положительной вещественной ча-
стью, то нулевое решение системы (2.257) неустойчиво.
Если уравнение (3.158) не имеет корней с положительной веществен-
ной частью, но имеется часть корней с нулевой вещественной частью, то мо-
жет иметь место как устойчивость (не асимптотическая), так и неустойчи-
вость.
Таким образом, вопрос об устойчивости нулевого решения системы
(2.257) сводится к исследованию корней характеристического уравнения
241
(3.158). Однако определение корней характеристических уравнений высоких порядков представляет значительные трудности, так как корни уравнений выше четвертого порядка не выражаются аналитически через коэффициенты уравнений. Для преодоления этих трудностей в разделе теории автоматиче-
ского управления, посвященному регулированию, разработано несколько правил (критериев устойчивости), позволяющих анализировать устойчивость систем без определения корней характеристического уравнения.
Существует два типа критериев устойчивости: алгебраические (Гурви-
ца и Рауса) и частотные (Михайлова, Михайлова-Найквиста и D-разбиения).
3.7.1. Алгебраические критерии устойчивости
Согласно теореме Гурвица для того чтобы все корни уравнения (3.158)
имели отрицательные действительные части, т. е. нулевое решение линейной автономной системы (2.257) было асимптотически устойчиво, необходимо и достаточно, чтобы матрица, составленная из коэффициентов уравнения
(3.158) и равная /8/
a1 a3 a5 |
a7 |
0 |
|
||||
|
|
a2 a4 |
a6 |
|
0 |
|
|
a0 |
|
|
|||||
0 a1 a3 |
a5 |
|
0 |
|
(3.163) |
||
|
|
|
0 |
|
|
||
|
|
|
|||||
|
0 |
0 0 |
0 |
|
|
|
|
|
an |
|
|||||
являлась положительно определенной, т. е. ее угловые миноры - определите-
ли Гурвица – k>0, k = 1, 2, . . ., n.
Для доказательства теоремы может быть использован результат Ляпу-
нова, объединяющий оба подхода.
Достаточно очевидно, что связь коэффициентов характеристического уравнения (3.158) с элементами исходной матрицы A (2.257) не является про-
стой.
Вместе с тем можно выбрать такой набор переменных состояния xi,
242
(i=1,2,. . ., n), что матрица A примет вид
|
0 |
1 |
0 |
0 |
|
0 |
|
|
0 |
0 |
1 |
0 |
|
0 |
|
A |
|
||||||
|
|
|
|
|
|
|
|
|
an |
an 1 |
an 2 |
an 3 |
|
|
|
|
a1 |
||||||
где элементы ai (i= 1, 2, . . ., n) аналогичны коэффициентам уравнения (3.158)
при a0 = 1.
Для доказательства целесообразно, выбрать исходную матрицу в виде
0 |
bn |
0 |
|
0 |
0 |
|
|
|
|
1 |
0 |
bn 1 |
|
0 |
0 |
|
(3.164) |
|
|
|||||||
0 |
1 |
0 |
|
|
|
|
|
|
B |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|||||
|
0 |
0 |
0 |
|
0 |
b2 |
|
|
|
|
|
||||||
|
0 |
0 |
0 |
|
1 |
b1 |
|
|
|
|
|
||||||
В /11/ показано, что определители Гурвица, полученные из матрицы
(3.164), связаны с коэффициентами bi (i=1,2,..., n) следующими зависимостя-
ми:
bi |
i 3 i |
, |
i 4,5, ,n. |
(3.165) |
|
|
|||||
|
|
|
|
|
|
|
i 2 |
i 1 |
|
|
|
Рассмотрим определенно положительную функцию Ляпунова V=xTPx,
где
b1b2 bn |
0 |
0 |
0 |
0 |
|
|
||
|
0 |
b1b2 bn 1 |
0 |
|
0 |
0 |
|
(3.166) |
|
|
|||||||
|
0 |
0 |
b1b2 bn 2 |
0 |
0 |
|
|
|
P |
|
|
|
|
0 |
0 |
|
|
|
|
|
||||||
|
0 |
0 |
0 |
b1b2 |
b |
|
|
|
|
2 |
|
||||||
|
0 |
0 |
0 |
|
0 |
b1 |
|
|
|
|
|
||||||
Используя уравнение x Bx, можно определить производную функ-
ции Ляпунова:
243
V |
x T ( P B B T P )x |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
0 |
b1 b2 bn |
|
0 |
|
0 |
0 |
|
|
|
|
|
|||
|
|
b1 b2 bn |
|
0 |
|
b |
1 b2 bn 1 |
|
0 |
0 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
0 |
b1 b2 bn 1 |
|
0 |
|
0 |
0 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
0 |
|
0 |
|
|
0 |
|
0 |
b1 b2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
0 |
|
b1 b2 |
|
|
|
|
|
|
x T |
|
|
|
|
|
|
b1 |
|
|
|
|
|||||||
|
|
|
|
0 |
|
b1 b2 bn |
0 |
|
0 |
|
0 |
|
|
x |
||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b1 b2 bn |
|
0 |
|
b1 b2 bn 1 |
0 |
|
0 |
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
0 |
|
b1 b2 bn 1 |
0 |
|
0 |
|
0 |
|
|
|||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
0 |
|
|
0 |
|
0 |
|
0 |
b1 b2 |
|
|||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
0 |
|
|
0 |
|
0 |
|
b1 b2 |
b |
2 |
|
|
||
|
|
|
|
|
|
|
|
|
1 |
|
||||||||
|
|
|
|
0 |
0 |
0 |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
0 |
0 |
0 |
|
0 |
0 |
|
|
|
|
|
|
|
|
(3.167) |
|
x T |
|
x 2 b12 x n2 . |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
|
0 |
2 b |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||
Производная V( x ) обращается в нуль, если xn=0, однако при этом все
xi (i = 1, 2, . . ., n-1) также обращаются, в нуль. Действительно, уравнение x Bx в рассматриваемом случае запишется в виде
|
dx1 |
|
|
|
0 bn x2 0 0 0 0 0 ; |
|
||||
|
|
|
||||||||
|
dt |
|
|
|
|
|
||||
|
dx2 |
|
x1 0 bn 1 x3 0 0 0 0 ; |
|||||||
|
|
|
||||||||
|
dt |
|
|
|
|
|
||||
|
dx3 |
|
0 x2 0 bn 2 x4 0 0 0 ; |
|||||||
|
|
|||||||||
|
dt |
|
|
|
|
|
||||
|
|
|||||||||
|
dxn 1 |
|
0 0 0 0 0 xn 2 0 b2 xn ; |
|||||||
|
dt |
|||||||||
|
|
|
|
|
|
|||||
|
dxn |
0 0 0 0 0 0 xn 1 b |
1 xn . |
|||||||
|
|
|||||||||
|
dt |
|
|
|
|
|
||||
Если xn = 0, то |
|
dxn |
0 и, |
следовательно, xn 1 |
0 . Далее из предпо- |
|||||
|
|
|||||||||
|
|
|
|
|
|
|
dt |
|
|
|
следней строчки следует, что xn 2 |
0 и т. д., т. е. xi=0 (i = 1, 2, . . ., n). |
|||||||||
Это значит, что всюду в области, где возможно движение системы,
функция V 0. По теореме Ляпунова система асимптотически устойчива,
если матрица Р (3.166) положительно определенная, т. е. все bi >0 и, следова-
244

тельно, по условию (3.166)
|
|
|
|
|
|
1 0; |
2 0; ; n 0 . |
|
|
|
|
y2 |
|
|
|
|
Таким образом, критерий Гурви- |
|
|
|
|
|
|
|
y1 ца доказан непосредственно на основе |
|
|
|
|
1 |
|
|
|||
1 |
|
|||||||
|
|
|
|
|||||
|
|
|
|
теоремы Ляпунова. |
||||
|
|
|
|
|
s |
|
|
|
|
s |
|
||||||
|
|
|
|
|
|
|
|
|
Пример 3.2. Рассмотрим линейную ав-
тономную систему (рис. 3.25), описываемую
Рис. 3.25. Расчетная схема системы
уравнениями
управления
|
|
|
|
|
|
dx |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
x2 |
; |
|
||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
dt |
|
|
|
(3.168) |
|||
|
|
|
|
|
|
|
|
. |
|||||
|
|
|
|
|
|
dx2 |
|
x1 |
x2 |
|
|
||
|
|
|
|
|
|
dt |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||
Матрица этой системы равна |
|
|
|
|
|||||||||
|
1 |
1 |
|
|
|
|
|
|
|
||||
|
A |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||
Характеристическое уравнение имеет вид |
|
|
|||||||||||
|
1 |
|
1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
1 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2 2 0. |
|
||||||
Матрица Гурвица |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
2 |
0 |
, |
(3.169) |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
откуда следует, что 1 2 0; 2 4 0, т. е. все определители Гурвица положительны и система уравнений (3.168) асимптотически устойчива в соответствие с критерием Гурви-
ца. Попутно отметим, что из приведенного выше характеристического уравнения второго порядка сразу следует вывод об устойчивости системы (3.168) в силу того, что вещест-
венные части двух комплексно-сопряженных корней отрицательны.
Простота примера иллюстрирует преимущества критерия Гурвица для линейных систем в сравнении с прямым методом Ляпунова.
245
Следствием из рассмотренной теоремы Гурвица является утверждение,
что корни характеристического уравнения (3.158) с положительными коэф-
фициентами ai >0 будут иметь отрицательные действительные части, когда среди определителей 1,…, n положительными будут все определители с четными или же нечетными индексами.
Образуем теперь матрицу /4/
c1 |
c3 |
c5 |
|||
|
|
c2 |
c4 |
||
c0 |
|||||
|
|
b3 |
b5 |
||
R b1 |
|||||
b0 |
b2 |
b4 |
|||
a |
1 |
a |
3 |
a |
5 |
|
|
|
|||
|
|
a2 |
a4 |
||
a0 |
|||||
|
|
||
|
|
|
|
|
(3.170) |
||
|
|||
|
|||
|
|
|
|
|
|
||
|
|
||
|
|
|
|
|
|
|
|
|
|
||
по следующему закону. Элементами нижней строки являются коэффициенты полинома (3.158) с четными номерами. Элементами второй снизу строки яв-
ляются коэффициенты полинома (3.158) с нечетными номерами. Элементы br
следующих двух строк определяются формулами
a |
1 |
a |
3 |
|
a |
1 |
a |
5 |
|
a |
1 |
a |
2k |
3 |
|
|
b0 |
|
,b2 |
|
, ,b2k |
|
, |
(3.171) |
|||||||||
a0 |
a2 |
|
a0 |
a4 |
|
a0 |
a2k |
2 |
. |
|||||||
b0 |
b2 |
b0 |
b4 |
b0 |
|
|
|
|
|
|||||||
b2k 2 |
|
|||||||||||||||
b1 |
|
|
|
,b3 |
|
|
|
, ,b2k 1 |
|
|
|
|
|
|
||
a1 |
a3 |
a1 |
a5 |
a1 |
a2k 3 |
|
||||||||||
Элементы cr определяются теми же формулами (3.171), в которых ве-
личины a и b заменены соответственно величинами b и с и так, далее. Эле-
менты каждых двух последующих строк выражаются через элементы двух предыдущих строк формулами (3.171).
Раус /13/ доказал, что для того, чтобы действительные части всех кор-
ней полинома (3.158) были отрицательными, необходимо и достаточно, что-
бы все элементы первого столбца матрицы (3.170) были положительными: a0 0,a1 0,b0 0,b1 0,c0 0,c1 0, . (3.172)
Условия устойчивости, получаемые из алгебраических критериев, ус-
ложняются с ростом порядка системы /6/. При этом для систем достаточно высокого порядка оказывается затруднительным выяснить влияние на устой-
246
чивость системы значений отдельных параметров, входящих в состав коэф-
фициентов уравнения. Это связано с тем, что, как правило, одни и те же па-
раметры одновременно входят в несколько коэффициентов уравнения систе-
мы. Поэтому критерии Рауса и Гурвица применимы для систем невысокого порядка и прежде всего для анализа устойчивости, когда надо определить,
устойчива ли система при известных значениях всех ее параметров. При ре-
шении задачи синтеза системы, когда требуется выбрать значения отдельных параметров системы, алгебраические критерии становится неудобным уже для систем выше четвертого порядка.
3.7.2. Частотные критерии устойчивости. Критерий Михайлова
Как уже отмечалось, определение устойчивости систем автоматическо-
го регулирования при помощи изложенных выше алгебраических критериев требует вычислений, трудоемкость которых быстро возрастает по мере по-
вышения порядка уравнения, описывающего движение системы. Ниже изла-
гаются получившие широкое распространение частотные критерии устойчи-
вости, применение которых не связано с трудоемкими вычислениями и кото-
рые являются значительно более наглядными.
Они основаны на взаимосвязи между характером переходных процес-
сов, возникающих при нарушении равновесия системы, и амплитудой и фа-
зой вынужденных колебаний, устанавливающихся в системе под воздействи-
ем синусоидально изменяющегося возмущающего воздействия.
Ниже приводится одно из наиболее простых доказательств /10/ крите-
рия устойчивости Михайлова, сформулированного им в 1938 г.
Обозначим через F( ) многочлен, составляющий левую часть характе-
ристического уравнения замкнутой системы (3.158), т.е. запишем:
F( ) a n a n 1 |
a |
a |
(3.173) |
|
0 |
1 |
n 1 |
n |
|
247
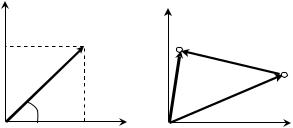
Многочлен F( ) можно представить в виде произведения простейших сомножителей вида (3.162), в соответствии с чем, каждый из корней r может быть изображен на комплексной плоскости в виде вектора, начинающегося в
|
Im |
|
Im |
начале |
координат и оканчи- |
||||||
|
|
вающегося в точке, координаты |
|||||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
- r |
|
||
i |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
которой |
соответственно равны |
||
|
r |
|
|
|
|
|
|||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
||||||
|
|
arg r |
Re |
|
r Re |
вещественной и мнимой частям |
|||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
данного корня, как это показано |
|
|
|
|
|
i |
|
|
|
|
|
||
|
|
|
|
|
|
|
б) |
на рис. 3.26, а. Вектор r может |
|||
|
|
а) |
|
|
|
|
|
||||
|
|
|
|
||||||||
|
|
|
|
|
|
быть также определен значени- |
|||||
Рис. 3.26. Представление корней характеристиче- |
|||||||||||
ского уравнения на комплексной плоскости |
ем его модуля | r|, равным дли- |
||||||||||
|
|
|
|
|
|
|
|
|
|
||
не этого вектора и значением его аргумента arg r равным углу, который об-
разует этот вектор с положительным направлением вещественной оси.
Зададимся произвольно некоторым комплексным числом , которое на рис. 3.26, б изображено соответствующим вектором. Тогда каждый из со-
множителей - r выражения (3.162) можно изобразить в виде вектора, начи-
нающегося в точке r и оканчивающегося в точке , представляющего собой
разность векторов и r,.
Будем придавать величине чисто мнимые значения, для чего поло-
жим в выражении (3.162) =j . Тогда многочлен F( ) преобразуется в F(j ):
F( j ) a0 ( j 1 )( j 2 ) ( j n ) |
(3.174) |
При этом любому произвольно выбранному значению числа будет соответствовать точка на мнимой оси комплексной плоскости корней, в ко-
торой будут оканчиваться концы векторов, изображающих сомножители вы-
ражения (3.174), как это показано на рис. 3.27,а.
Как известно, при умножении векторов их модули перемножаются, а
аргументы складываются. Поэтому аргумент вектора F(j ) равен сумме ар-
гументов его сомножителей:
248
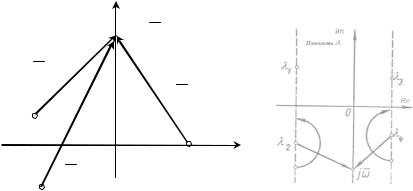
|
|
|
|
|
|
arg F( j ) arg( j 1 |
) arg( j 2 ) arg( j n ). |
(3.175) |
|||||||||||
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
Будем теперь |
||
Пл. |
|
|
|
|
|
|
j |
|
|
|
|
|
|
изменять значение |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
j |
|
2 |
|
|
|
|
|
j |
|
1 |
|
|
и следить за из- |
||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
менением аргумен- |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тов векторов (j - r). |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
0 |
|
|
1 |
Re |
|
Как видно из рис. |
||||
|
|
|
j |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.27, б, если корень |
||||
|
|
|
|
|
а) |
|
|
|
|
|
|
б) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
характеристическо- |
||||||
Рис. 3.27. Сомножители функции F(j ) (а) и приращение |
|||||||||||||||||||
|
|
||||||||||||||||||
аргумента вектора (j - i) при изменении от – до + (б) го уравнения, на-
пример, 2 лежит слева от мнимой оси плоскости , то при изменении от –
до + соответствующий ему вектор (j — 2) повернется на угол + в по-
ложительном направлении (против часовой стрелки). Если же корень, на-
пример, 4, лежит справа от мнимой оси, то соответствующий ему вектор (j -
r) при изменении от – до + повернется на угол - .
В соответствии с (3.175) приращение аргумента вектора F(j ) равно сумме приращений аргументов его сомножителей. Поэтому если все n кор-
ней характеристического уравнения лежат слева от мнимой оси, то прираще-
ние аргумента вектора F(j ) при изменении от – до + будет равно:
arg F( j ) n , |
(3.176) |
|
. |
|
|
|
|
|
Если же среди корней характеристического уравнения окажется m кор-
ней, лежащих справа от мнимой оси, то приращение аргумента F(j ) будет меньше n и составит
arg F( j ) ( n 2m ) , |
(3.177) |
|
. |
|
|
|
|
|
На основании изложенного можно сформулировать следующий критерий устойчивости систем автоматического регулирования:
249

Система автоматического регулирования, движение которой описыва-
ется линейным дифференциальным уравнением n-го порядка будет устойчи-
ва тогда и только тогда, если при изменении от – до + изменение ар-
|
гумента F(j ) составит n . |
|
|||
|
О |
величине |
изменения |
аргумента |
|
|
функции F(j ) для заданной системы мож- |
||||
|
но судить по форме кривой, которую опи- |
||||
|
сывает на плоскости конец вектора F(j ) |
||||
|
при изменении в нужных пределах. |
||||
Рис. 3.28. Годографы Михайлова |
Эта кривая называется характеристи- |
||||
устойчивых систем |
|||||
|
|
|
|
||
|
ческой |
кривой или |
годографом |
функции |
|
F(j ). Примерный вид годографов функции F(j ) для устойчивых систем,
описываемых уравнениями до пятого порядка, показан на рис. 3.28. Для большей наглядности чертежа все годографы исходят из одной и той же точ-
ки, т. е. an у всех характеристических уравнений приняты одинаковыми.
Из рисунка видно, что, например, при изменении от – до + век-
тор F(j ) при характеристическом уравнении третьего порядка поворачива-
ется на угол 3 , что при n = 3 свидетельствует об устойчивости рассматри-
ваемой системы.
Для построения годографа функции F(j ) в многочлене (3.173) после
замены на j выделяются вещественная и мнимая части.
Поскольку вещественная часть U( ) функции F(j ) содержит только четные степени аргумента , то при изменении знака на обратный U( ) не
изменяется, т. е. |
|
U( ) U( ). |
(3.178) |
Функция V( ), содержащая только нечетные степени при изменении |
|
знака изменит свой знак на обратный |
|
V( ) V( ). |
(3.179) |
250 |
|
