3832

На рис. 3.10 приведены АФЧХ интегрирующих звеньев при =2 и =3.

Сопоставляя их с рис. 3.8, б, нетрудно придти к выводу, что увеличение

(порядка астатизма) приводит к повороту АФЧХ на угол по часовой

2

стрелке. На столько же изменяется и ФЧХ соответствующего звена.

Из выражения (3.50) нетрудно получить

Логарифмируя формулы (3.52), получим

L( ) 20lg H( ) 20 lg ; ( )

2 .

Таким образом, ЛАЧХ звеньев имеет наклон -20 дБ/дек, а ЛФЧХ

идет по оси .

2

Реальные интегрирующие звенья обычно обладают определенной инерцион-

ностью, вследствие чего их выходная вели-

чина не равна точно интегралу от входной

Рис. 3.10. АФЧХ интегрирующих величины. Передаточная функция реально-

звеньев: а – при =2; б – при =3

го интегрирующего звена содержит инер-

ционную (балластную) составляющую и имеет вид:

s(Ts 1)

Поэтому реальное интегрирующее звено не является типовым элемен-

тарным звеном, т. к. его можно представить в виде соединения типовых звеньев – идеального интегрирующего, усилительного и апериодического первого порядка.

201

3.1.6. Колебательное звено

Колебательное звено получается при наличии двух соединенных емко-

стей, способных запасать количество энергии двух видов и взаимно обмени-

ваться этими количествами. Если в результате колебаний запас энергии, по-

лученный в начале возмущения, в звене уменьшается, то колебания затухают и звено является устойчивым. Колебательное звено характеризуется переда-

точной функцией вида

где k - коэффициент усиления; T - постоянная времени; - коэффициент за-

тухания.

Пусть Т1 и Т2 связаны следующим условием малости Т2 по сравнению с

1

являются комплексными.

202

Уравнение установившегося (статического) режима этого звена, со-

гласно (3.58), имеет вид:

но действительная, мнимая части корней (3.59) характеристического уравне-

ния (3.57) и их отношение (тангенс фазового угла).

На рис. 3.11, а показаны переходные характеристики колебательного звена для ряда значений . Как видно из рисунка, с ростом значения коле-

бательность переходного процесса уменьшается, исчезая совсем при 1.

По экспериментально снятой переходной характеристике можно найти значения параметров T1, Т2 и k уравнения звена:

Входящие сюда величины и вычисляются непосредственно по пе-

реходной характеристике следующим образом.

Согласно (3.61) величина , являясь частотой колебаний, равна

где – период колебаний, определяемый по переходной характеристике

(рис. 3.11, а). Величина в соответствии с (3.61) характеризует степень зату-

хания колебаний и может быть найдена из выражения

203

Рис. 3.11. Характеристики колебательного звена

ymax2 e

где ymax1, ymax2 – амплитуды колебания у относительно конечного устано-

вившегося его значения, отстоящие друг от друга на время, равное периоду

колебаний (рис. 3.11, а).

Отсюда

Амплитудно-фазовая частотная характеристика согласно (3.55)

Соответствующая характеристика показана на рис. 3.11, в.

Частотные характеристики звена определяются выражениями, сле-

дующими из (3.65):

Согласно (3.68) первая асимптота идет параллельно оси абсцисс на вы-

соте 20lgk.

При >>1, пренебрегая T22 2 и 1 по отношению к T14 4, перепишем

(3.67) в виде

колебательного звена при k=1 приведена на рис. 3.11, г.

205

При 0,4 < < 0,7 расхождение между асимптотической и истинными ЛАЧХ не превышает 3 дБ, как и в случае апериодического звена (см. рис. 3.7,

г). Поэтому для звеньев с таким значением можно пользоваться асимптоти-

ческими ЛАЧХ. При других значениях асимптотическую ЛАЧХ корректи-

руют с помощью готовых графиков поправок, дающих разность между ис-

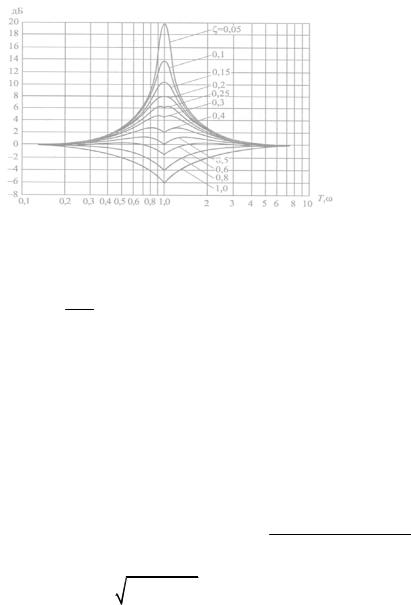
тинной и асимптотической ЛАЧХ. Эти графики приведены на рис. 3.12.

ЛФЧХ колебательного звена при различных значениях

приведены на рис. 3.11, г вме-

сте с ЛАЧХ.

при T2 1, т.е. при невыполненном условии (3.56).

2T1

В этом случае согласно (3.59) характеристическое уравнение, соответ-

ствующее дифференциальному уравнению (3.58), имеет не комплексные, а

отрицательные действительные корни. Поэтому такое звено уже не является колебательным. Оно называется апериодическим звеном второго порядка.

Передаточная функция (3.55) в этом случае может быть представлена в виде

(T3s 1)(T4 s 1)

Операторное дифференциальное уравнение второго порядка, соответ-

ствующее (3.70), может быть заменено двумя операторными дифференци-

альными уравнениями первого порядка:

206

(T3s 1)z kx,

(T4 s 1)y z,

где z – промежуточная переменная. Это означает, что рассматриваемое апе-

риодическое звено второго порядка может быть заменено в структурной схе-

ме двумя звеньями первого порядка, описываемыми этими уравнениями, и,

следовательно, его нельзя считать элементарным звеном.

3.1.8. Консервативное звено

Еще одним частным случаем звена, описываемого уравнением (3.58),

является так называемое консервативное звено. У этого звена T2 = 0 и, следо-

вательно, дифференциальное уравнение имеет вид:

2

T2 d y y kx (3.71) dt2

а передаточная функция –

Переходная характеристика такого звена представляет собой незату-

хающие колебания.

где Td – постоянная времени дифференцирования.

Таким образом, в соответствии с названием выходная величина такого звена пропорциональна производной от входной величины.

Переходная функция согласно (3.73)

Передаточная функция

207

Сравнивая (3.31) и (3.84) можно придти к выводу, что ЛАЧХ диффе-

ренцирующего звена первого порядка представляет собой зеркальное ото-

бражение относительно оси Т соответствующих ЛАЧХ апериодического звена.

Передаточная функция дифференцирующего звена второго порядка

имеет вид:

Из (3.86) можно получить переходную функцию звена (рис. 3.14, б) в виде

Имея в виду выражение (3.88)), можно построить АФЧХ для диффе-

ренцирующего звена второго порядка (см. рис. 3.15, б). На основании выра-

жения (3.88) определим

210