3832

С u dx :

Сократив уравнения (2.37) и (2.40) на dx, получим систему двух линей-

ных дифференциальных уравнений в частных производных, описывающую процесс в длинной линии при действии на ее входе любого напряжения и при произвольной нагрузке на ее конце (выходе);

Время t не входит явно в уравнения однородной линии (2.41). Поэтому процесс в ней при одном и том же входном напряжении протекает всегда одинаково, независимо от момента его начала. Это означает, что длинная ли-

ния представляет собой стационарную линейную систему. Следовательно, ее динамические свойства полностью определяются ее передаточной функцией

W(s). Для определения передаточной функции W(s) приложим ко входу ли-

нии напряжение, изменяющееся по показательному закону u(t,0) est , и бу-

дем искать решение системы уравнений (2.41) в виде

где (s,x) и (s,x) - некоторые неизвестные функции, не зависящие от време-

ни. При этом учтем граничные условия в начале и конце линии:

91

Второе граничное условие выбрано из соображения, что длинные ли-

нии, применяющиеся в системах автоматического управления, обычно на-

гружены или чистым омическим сопротивлением, или последовательным со-

единением омического и индуктивного сопротивлений.

Подставляя выражения u(t,x), i(t,x) из (2.42) в уравнения (2.41), после сокращения на est получаем для определения функций (s,х) и (s, х) урав-

нения

Эти уравнения образуют систему двух обыкновенных линейных диф-

ференциальных уравнений с постоянными коэффициентами, зависящими от параметра s. Применяя обычный метод интегрирования систем линейных уравнений (см. также 2.3.2.) с постоянными коэффициентами, составляем ха-

рактеристическое уравнение:

находим 1,2= (s). Этим двум корням характеристического уравнения (2.45)

соответствуют два частных интеграла системы уравнений (2.44):

Для определения постоянных а1 и а2 подставим эти частные интегралы по очереди в любое из уравнений (2.44) и потребуем, чтобы оно обратилось в тождество относительно х. Тогда, полагая для краткости

92

получим a1= - (s), а2 = (s). Таким образом, мы нашли два линейно независи-

мых частных интеграла системы уравнений (2.44). Общий интеграл этой сис-

темы уравнений определяется формулами

граничными условиями (2.43). Подставляя в них выражения (2.42) и сокра-

щая на est , приведем эти условия к виду

Передаточная функция однородной длинной линии W(s) в случае, ко-

гда выходной переменной является напряжение на конце линии и(t,l), на ос-

новании (2.42) будет равна

Подставляя сюда выражения (2.52) постоянных с1 и c2, получаем окон-

чательное выражение для передаточной функции W(s):

Выражение (2.54) передаточной функции W(s) показывает, что в общем случае однородная длинная линия представляет собой сложный динамиче-

ский элемент, обладающий, в зависимости от соотношения величин ее ос-

новных параметров R, L, C, G и вида нагрузки ZH(s), различными свойства-

ми. Проанализируем, как изменяется передаточная функция W(s) в зависимо-

сти от изменения вида нагрузки и выбора определенных сочетаний основных параметров линии.

Для изучения динамических свойств самой длинной линии, ни с чем не соединенной, следует предположить, что нагрузка на конце линии отсутству-

ет. Это равноценно случаю, когда сопротивление нагрузки бесконечно вели-

ко, т. е. RH = . Полагая в (2.54) RH = находим передаточную функцию длинной линии, рассматриваемой как изолированное звено автоматической системы:

Выбирая параметры длинной линии и нагрузку на ее конце соответст-

вующим образом, можно получить линию с желательными динамическими свойствами.

В системах автоматического управления обычно применяются только так называемые согласованные линии, т. е. такие линии, которые не дают от-

ражения прямого сигнала, приходящего к концу линии, от нагрузки. Линия становится согласованной, когда нагрузка ZH(s) выбирается равной волново-

Из этого равенства видно, что согласованности линии в общем случае можно добиться только при каком-нибудь одном значении s так как это ра-

венство не является тождеством относительно s. Поэтому для обеспечения

94

согласованности линии обычно пользуются переменным током определенной частоты 0 и сопротивление нагрузки выбирают из условия (2.56) при s = j 0.

В этом случае при передаче сигналов переменным током частоты 0 линия будет работать в режиме бегущей волны. Полагая (j 0 )= +j , получим

W( j 0 ) e l( j ) . (2.57)

Сигнал в такой линии распространяется со скоростью 0/ и ослабляет-

ся в е раз на единицу длины линии.

Полной согласованности линии при любом значении s можно добиться,

если выбрать ее параметры так, чтобы удовлетворялось условие RC=LG.

выражение (2.54) для передаточной функции длинной линии примет вид

W ( s ) e l RG e sl LC . (2.59)

Сигнал распространяется по такой линии без искажения со скоростью,

равной 1LC , и ослабляется в e RG раз на каждую единицу длины линии.

Такие линии обычно применяются в виде реальных линий задержки.

Чтобы получить значительное время задержки сигнала, необходимо выбрать большую длину линии (десятки — сотни метров), что может привес-

ти к большим трудностям в выборе основных параметров линии, позволяю-

щих выполнить условия RC=LG. Кроме того, линия получается громоздкой.

Часто применяют непрерывную спиральную линию задержки, у которой изо-

лированный внутренний кабель оплетается спиральным экраном. Такая ли-

ния имеет значительные собственные индуктивность и емкость при сравни-

тельно короткой общей длине. Поэтому ослаблением амплитуды сигнала в

95

ней можно пренебречь (так как величины l, R, G будут малыми, а L и С -

большими).

2.2.4. Модели «вход-выход» дискретных систем. Z-преобразование

Так как входная переменная х(t) действует на дискретную систему только в определенные моменты времени tk (k = 0, ±1, =±:2, . . .), то ее выход-

ная переменная является функцией времени и значений x(tk) (k=0, ±1, ±2, . . .)

входной переменной /4/. Поэтому при анализе импульсных систем удобнее заменить непрерывную функцию x(t), характеризующую внешнее воздейст-

вие, соответствующей ей решетчатой функцией x[nT], т. е. такой функцией,

значения которой изменяются лишь при дискретных равноотстоящих друг от друга значениях независимой переменной t /26/. Между этими значениями

решетчатая функция равна нулю.

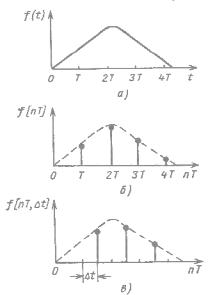
На рис. 2.8, а изображена непрерывная функция f(t), а на рис. 2.8, б — соответствую-

щая ей решетчатая функция f[nT], где n — це-

лое число, а Т - положительная величина, оп-

ределяющая расстояние между соседними

дискретными значениями независимой пере-

менной. Решетчатая функция получается из непрерывной, если положить t=nT.

Помимо простых решетчатых функций

при анализе импульсных систем используются

Рис. 2.8. Непрерывная (а), ре-

шетчатая (б) и смещенная ре- так называемые смещенные решетчатые функ-

шетчатая (в) функции

ции f[nT, t] (рис. 2.8, в), которые получаются из непрерывных функций, если положить в них t=nT+ t, где 0 t T характе-

ризует сдвиг аргумента.

Значения ординат непрерывной функции, совпадающих с ординатами решетчатых функций, называют дискретами (на рис. 2.8 выделены точками).

96

Одной и той же решетчатой функции могут соответствовать различные непрерывные функции, которые называют огибающими решетчатой функции

(рис. 2.9). Простейшей огибающей является ступенчатая функция, получаю-

жду дискретными значениями независимой переменной равным единице.

Для этого введем безразмерную переменную t t / T [t] , тогда

f(t ) f(Tt ). Или, для сокращения записи, f(Tt ) f(t ) f [t].

Решетчатая функция f[n] с безразмерным аргументом, где n=1, 2, 3, ...

будет совпадать с функцией f(Tt ) при значениях t n.

Скорость изменения решетчатой функции характеризуется ее первой разностью f[n], или разностью первого порядка, аналогично тому; как ско-

рость изменения непрерывной функции характеризуется первой производ-

ной. При этом различают прямые и обратные разности.

Прямая разность первого порядка решетчатой функции f[n] определя-

В общем виде k-я разность (разность k-го порядка)

97

Из сопоставления выражений (2.62) для прямой и обратной разностей следует

k f [n] k f [n 1] .

Соотношение между решетчатой функцией у[п] и ее разностями опре-

деляет уравнение в конечных разностях, или разностное уравнение. Если это соотношение линейно, то такое уравнение называют линейным. Линейное

Если в уравнении (2.63) заменить разности решетчатой функции их

значениями в соответствии с соотношением (2.62), то получится иная запись этого уравнения:

Разностные уравнения (2.63) и (2.64) с правой частью, отличной от ну-

ля, называются неоднородными. Разностные уравнения с правой частью,

равной нулю, называются однородными. Разностное уравнение, содержащее

у[п] и y[n+k], называют уравнением k-го порядка.

Из выражения (2.64) видна связь между разностными и дифференци-

альными уравнениями. Если дифференциальные уравнения связывают зна-

чения функции у(t), соответствующие значениям аргумента t, отстоящим

98

друг от друга на бесконечно малую величину, то разностные уравнения свя-

зывают значения функции у[п], соответствующие дискретным значениям ар-

гумента n, отстоящим друг от друга на конечную величину (в нашем случае единицу).

Обозначим /4/ реакцию дискретной линейной системы на кратковре-

менное входное возмущение, равное единице и действующее только в тече-

ние времени действия k-го импульса, через gk(t). Тогда ее реакция на кратко-

временное возмущение, равное х(tk) и действующее только в течение време-

ни действия k-го импульса, будет на основании принципа суперпозиции рав-

на gk(t)х(tk). Реакция дискретной линейной системы на всю последователь-

ность импульсов, модулированных входным возмущением х(tk), в силу прин-

ципа суперпозиции определится формулой

k

Это и есть основная формула, выражающая зависимость выходной пе-

ременной дискретной линейной системы от входного сигнала.

Функции gk(t) полностью характеризуют дискретную линейную систе-

му, так как, зная эти функции, можно вычислить реакцию дискретной линей-

ной системы на любое входное возмущение х(t). Функции gk(t) определяют долю, или удельный вес, значений входной переменной, действующих в раз-

личные моменты времени tk, в формировании выходной переменной системы в любой момент времени t. Вследствие этого функции gk(t) называются весо-

выми коэффициентами дискретной линейной системы.

Дискретизацию входных или промежуточных сигналов можно пред-

ставить их модуляцией (см. п. 1.4.4), где в качестве несущей частоты высту-

пает импульсная последовательность, а в качестве огибающей – входной сигнал (рис. 2.9).

99

ную последовательность реального модулятора u(t). На рис. 2.10, б представ-

лена альтернативная форма графического изображения ИИЭ. Идеальный им-

пульсный элемент представляет собой амплитудно-импульсный модулятор,

непрерывный входной сигнал которого x(t) модулирует несущую последова-

тельность мгновенных -импульсов. Таким образом, на выходе ИИЭ форми-

руется последовательность мгновенных импульсов не единичной, а перемен-

ной площади, являющейся мерой входного сигнала в дискретные моменты времени.

Формирующий элемент вырабатывает дискретный сигнал, представ-

ляющий собой реакцию линейного элемента на импульсы ИИЭ. ФЭ, назы-

ваемые также фиксаторами или экстраполя-