3832

зом, стационарны. Изменение их состояния происходит в силу накопленной ранее энергии. Автономную систему можно представить в виде, изображен-

ном на рис. 1.11 при g(t) = 0, т.е. имеющей выход (выходы), но не имеющей входов. Движения автономной системы называют свободными.

Постановка задачи анализа динамической системы содержит составле-

ние следующих моделей:

1. Объект и элементы системы управления, обычно описываемые урав-

нениями, отражающими применение известных законов физики и техники.

Параметры моделей задаются либо статистическими характеристиками, либо множествами возможных значений. Линейные объекты или элементы систем описываются чаще всего передаточными функциями.

2.Системы автоматического управления, содержащей модели объекта

иэлементов, а также их связи. При анализе систем автоматического управле-

ния учитываются также краевые (начальные и конечные) условия, которые могут быть детерминированными, случайными (определяться своими стати-

стическими характеристиками) или описываться множествами возможных значений; внешние воздействия; измерительная система; алгоритм управле-

ния, определяющий характер использования информации об измерении, спо-

соб выработки и приложения управляющих воздействий; цель управления,

выраженную, как правило, в виде некоторого критерия качества, отражающе-

го требования, предъявляемые проектировщиком к системе.

Важно /2/ также обратить внимание на то, что модели для целей управ-

ления обычно отличаются от тех, которые предназначаются для других це-

лей, например, проектирования самого процесса. Пригодные для целей управления модели описываются динамическими количественными соотно-

шениями между входами и выходами объекта. При этом внутренние детали моделируемой системы уместны только тогда, когда они необходимы для достижения желаемой цели. В качестве примера можно указать на проблему учета свойств исполнительного механизма в процессе моделирования. Ис-

71

полнительные механизмы во многих случаях существенно нелинейны и об-

ладают собственными динамическими характеристиками, которые, в некото-

рых случаях могут фактически доминировать над характеристиками объекта и других элементов системы. Эта ситуация часто возникает в системах с кла-

панами, гидравлическими приводами и управляемыми выпрямителями. По этой причине впоследствии, когда мы будем говорить о модели системы,

следует понимать, что она также включает и модели исполнительных меха-

низмов, если это необходимо.

Сложность процессов в реальных системах определяет приближен-

ность их математического описания, которая ограничивается только доста-

точностью принятой модели для достижения поставленной цели анализа или синтеза. В /2/ вводятся несколько понятий, определяющих уровень целесооб-

разности использования и адекватности моделей:

Номинальная модель – приблизительное описание объекта, ис-

пользуемое для проектирования системы управления.

Эталонная модель – более полное описание объекта. Оно вклю-

чает и другие особенности, не используемые для проектирования системы

управления, но имеющие прямое отношение к полученным характеристикам.

Ошибка модели – различие между номинальной моделью и эта-

лонной моделью. Детали этой ошибки могут быть неизвестны, но можно по-

лучить различные оценки ее величины.

Эталонную модель зачастую рассматривают как истинный объект, од-

нако необходимо обратить внимание на то, что эталонная модель также не является точным описанием реального объекта, и, следовательно, нужно быть осторожным при интерпретации результатов.

Решить, какая номинальная модель целесообразна, обычно нелегко.

Пока скажем лишь, что она должна включать относящиеся к управлению особенности динамики объекта и его нелинейности.

При разработке математических моделей выделяют два подхода. Пер72

вый подход заключается в постулировании структуры модели (задании опе-

ратора, см. 1.4.2) и определении параметров оператора методом так называе-

мого «черного ящика». Параметры модели при этом подходе меняются либо эмпирически, либо на основе какого-то алгоритма, пока динамическое пове-

дение модели и объекта достаточно хорошо не совпадут.

Альтернативный подход к задаче моделирования состоит в том, чтобы использовать физические законы (типа сохранения массы, энергии и импуль-

са) для построения модели. В этом подходе используется факт, что в любой реальной системе имеются основные феноменологические законы, которые определяют отношения между всеми ее сигналами. Эти законы касаются природы системы и могут включать физику, химию и экономическую тео-

рию.

Практически идеи черного ящика и феноменологические комбиниру-

ются при создании модели. Феноменологическое понимание часто является ключевым в понимании динамики (включая доминирующие параметры), не-

линейностей и существенных временных изменений в данной системе. Это может помочь в первоначальном выборе сложности модели. С другой сторо-

ны, подход с использованием черного ящика часто позволяет выбрать модели для тех частей объекта, где соответствующая физика процессов настолько сложна, что трудно подобрать соответствующую феноменологическую мо-

дель.

Суммируя, можно сказать, что модели для систем управления часто весьма просты по сравнению с истинными процессами и обычно объединяют физические соображения с экспериментальными данными, выраженные в виде дифференциальных уравнений (с непрерывным временем), разностных уравнений (дискретное время), или комбинации их (гибридные или импульс-

ные системы). Эти модели связывают входы объекта с отдельными его выхо-

дами и имеют дело с ограниченным описанием системы в процессе ее изуче-

ния.

73

Для одномерных систем входные и выходные переменные являются скалярами /7/. Эти и некоторые другие представления операторов рассматри-

ваемого класса моделей могут быть приняты за основу задания динамиче-

ских свойств в терминах «вход-выход».

Для многомерных систем (рис. 2.2), входные и выходные переменные которых являются векторами, динамические свойства описываются в терми-

нах «вход-состояние-выход».

Если для конкретных исследований та или иная форма оказывается бо-

лее предпочтительной, ставится и решается задача перехода от одной формы к другой, например задача построения временных и частотных характеристик по дифференциальному уравнению или передаточной функции.

Заключительный момент в этом обсуждении касается идеи робастности

(устойчивости к нарушениям исходных предпосылок). Проектирование систе-

мы управления обычно основывается

Рис. 2.2. Многомерная система автоматического управления на номинальной модели объекта. Од-

нако регулятор будет использоваться для управления реальным объектом.

Одна из проблем проектировщика – получить регулятор, который при работе с реальным объектом продолжает функционировать так, как предсказано мо-

делью, без существенного ухудшения. Когда дело обстоит именно так, мы будем говорить, что разработали робастный регулятор. Чтобы достичь роба-

стности, обычно необходимо иметь меру ошибки моделирования, чтобы со-

ответствующие предосторожности могли бы быть приняты еще на стадии проектирования /2/.

74

2.2.Непрерывные стационарные системы управления

2.2.1.Модели «вход-выход» непрерывных систем. Составление и линеаризация дифференциальных уравнений элементов с

сосредоточенными параметрами

Как уже отмечалось, математическое описание, необходимое для ис-

следования процесса управления или регулирования, осуществляется обычно с помощью дифференциальных, интегральных, разностных или алгебраиче-

ских уравнений.

Инерционные системы и элементы систем непрерывного регулирова-

ния описываются обычно дифференциальными или интегральными уравне-

ниями, называемыми уравнениями динамики. Безынерционные элементы, а

также поведение системы регулирования в установившемся режиме при по-

стоянных воздействиях описываются алгебраическими уравнениями, назы-

ваемыми уравнениями статики /5/.

В общем случае дифференциальные уравнения, описывающие поведе-

ние элемента или системы регулирования, нелинейны. Но при малых откло-

нениях координат системы от положения равновесия нелинейные уравнения можно приближенно заменить линейными уравнениями. Процесс замены не-

линейного уравнения линейным называется линеаризацией дифференциаль-

ного уравнения.

Стимулом попытаться приблизить нелинейную систему к линейному представлению является то, что теория и практика линейного управления яв-

ляются более завершенными и более простыми, чем в нелинейном случае.

Полезный способ получить эти линейные модели - начать с нелинейной мо-

дели и затем построить линейное приближение в окрестности выбранной ра-

бочей точки. При этом, чем меньше отклонения координат системы от со-

стояния равновесия, тем точнее линеаризованные уравнения описывают про-

цесс. Так как исследование линейных уравнений позволяет сделать полезные

75

обобщающие выводы о системе, линейная теория автоматического управле-

ния имеет очень большое значение для приближенного исследования систем.

Рассмотрим звено (рис. 2.3), оператор которого нелинеен, и уравнение статики описывается зависимостью y = (x) /6/.

Пусть установившийся режим звена соответст-

вует значениям входной и выходной величин Xо и Y0

(рис. 2.3) и отклонения x от X0 в процессе работы звена достаточно малы. В этом случае исходную не-

линейную зависимость y = (x) можно разложить в ряд Тейлора в окрестностях точки исходного устано-

вившегося режима и, отбросив члены ряда выше первого порядка малости,

получить следующую приближенную зависимость:

d

где – значение производной функции (x) по x при подстановке в

dx x X0

выражение этой производной x = X0.

Это уравнение можно переписать в таком окончательном виде:

d

где X=x-X0, Y=y-Y0, k .

dx 0

Проведенная линеаризация имеет простую графическую интерпрета-

цию. Она соответствует, как показано на рис. 2.3, замене действительной не-

линейной характеристики касательной к ней в точке, соответствующей уста-

новившемуся режиму. Коэффициент k в уравнении (2.2) равен тангенсу угла наклона этой касательной относительно оси абсцисс. Поэтому его величина может быть найдена и графическим построением без нахождения аналитиче-

ского выражения для исходной нелинейной зависимости (x).

76

Рассмотрим теперь более общий случай, когда звено описывается не-

линейным уравнением, включающим производные по времени от входной и выходной величин:

( x,x ,x , ,y,y ,y , ) 0

Разложив, как и прежде, нелинейную функцию, находящуюся в левой части уравнения, в ряд Тейлора в точке установившегося режима и отбросив члены выше первого порядка малости, получим следующее линейное диффе-

ренциальное уравнение для приращений переменных:

Подобная процедура линеаризации нелинейных звеньев приводит к приближенному описанию их линейными дифференциальными уравнениями в отклонениях (в вариациях).

Допустимость такой линеаризации ограничена следующими очевид-

ными условиями. Во-первых, она применима только для малых отклонений,

т. е. полученные в результате линеаризации уравнения пригодны для при-

ближенного исследования только таких режимов в системах, при которых переменные величины на входе звеньев претерпевают достаточно малые от-

клонения от установившихся значений. При этом точность исследования рас-

тет с уменьшением этих отклонений.

Во-вторых, поскольку такая линеаризация основана на разложении функции в ряд Тейлора, она применима только к непрерывно дифференци-

руемым нелинейностям. Поэтому такие нелинейности называются линеари-

зуемыми. Нелинейные звенья, не удовлетворяющие этому требованию, назы-

ваются существенно нелинейными. К существенно нелинейным звеньям, на-

пример, относятся звенья с прерывистыми характеристиками типа релейных

характеристик и с неоднозначными характеристиками типа петли гистерези77

са.

Особенности процессов в нелинейных системах регулирования, кото-

рые не могут быть выявлены с помощью линейной теории, рассматриваются далее.

Для получения математического описания системы составляются сна-

чала дифференциальные уравнения отдельных ее звеньев, а затем на основа-

нии этих уравнений и уравнений связи - дифференциальное уравнение сис-

темы в целом, после чего его линеаризация.

Рассмотрим /24/ методику составления линейных дифференциальных уравнений объектов систем управления с сосредоточенными параметрами на примерах.

Пример 2.1. Динамическая модель термической печи (рис. 2.4).

Регулируемой величиной объекта является температура внутри печи °С. Нагрев печи осуществляется электронагрева-

телем с сопротивлением R, по которому протекает ток I. Пусть

вн – температура внешнего помещения.

Введем следующие допущения:

- будем полагать, что во всех точках объема печи темпе-

ратура одинакова;

Рис. 2.4 Модель - исследование проводится при небольших отклонениях теплового объекта

тока I от базовой постоянной величины Iо, т. е. I=Iо+ I и I

<<Iо, где I может быть положительным и отрицательным.

Электрическая энергия RI2dt, поступающая в печь за бесконечно малый промежу-

ток времени dt, расходуется на нагрев печи и на внешнее излучение. Пусть теплоемкость печи равна С Дж/град. Для нагрева печи на один градус необходимо затратить С Дж, а при нагреве на d затрачивается С d Дж тепла. Потери энергии на излучение в одну секунду пропорциональны излучающей поверхности F печи и разности температур ( - вн), т. е.

равны СсF( - вн), где Сс – коэффициент излучения, имеющий размерность Вт/(м2•град).

За время dt потери составят СсF( - вн) dt.

Согласно закону сохранения энергии имеем:

78

Допустим, что при некоторой температуре о печи и токе I=Iо ( I =0) приток энер-

гии в печь идет целиком на излучение наружу. Тогда температура печи не меняется, вели-

Обозначим превышение температуры над о через :

Таким образом, найдено дифференциальное уравнение, связывающее во времени отклонения I (входную величину объекта) и (выходную величину объекта) от посто-

янных установившихся значений Iо и о.

79

где T – постоянная времени объекта, имеющая размерность времени (с), К – коэффициент усиления, x, y – входная и выходная переменные.

Полученное дифференциальное уравнение первого порядка феномено-

логического типа, имеющее степень свободы ½, характерно для объектов,

динамические свойства которых исследуются на основе фундаментальных законов сохранения энергии, массы и т.д. При этом сами объекты рассматри-

ваются структурно целостными, нерасчленимыми. В то же время, имеется значительное число структурно сложных объектов управления, имеющих большую степень свободы, и, следовательно, описываемых более сложными уравнениями движения. Рассмотрим движения объекта (вибровозбудителя) с

одной степенью свободы, происходящие под действием не только добавоч-

но и кинетической и потенциальной энергии.

Пример 2.2. Динамическая модель электромагнитного вибровозбудителя /25/.

Характерной особенностью динамики электромагнитного вибровозбудителя, при-

меняемого, например, для возбуждения колебаний виброплощадок, конвейеров, и т.д., является взаимосвязь механических колебаний и электро-

магнитной вынуждающей силы.

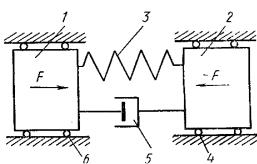
Простейшая расчетная схема однотактной системы приведена на рис. 2.5. Здесь реактивная 1

и корпусная 2 части благодаря идеальным связям

4 и 6 движутся поступательно в горизонтальном

Рис. 2.5. Расчетная схема

направлении. Реактивная и корпусная части со-

единены между собой пружиной 3 и демпфером 5, моделирующем диссипативные сопро-

тивления в системе.

80