3832

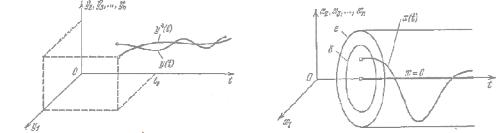
при этом невозмущенным движением будет xi = 0, а решение (2.250) называ-

ют тривиальным. Переменные xi, (i= 1, 2, ..., n) являются координатами со-

стояния системы.

Попутно можно отметить, что формально уравнение (2.250) совпадает с линеаризованными уравнениями нелинейной системы (см. 2.2.7), т.е. резуль-

тат линеаризации можно рассматривать возмущенным движением относи-

тельно некоторой опорной траектории. Конкретный вид уравнений (2.250)

зависит от вида установившегося процесса y*i (t ), поэтому, исследуя эти уравнения необходимо оговаривать, об устойчивости какого установившего-

ся режима или невозмущенного движения y*i (t ) идет речь.

Геометрически невозмущенное (установившееся) движение y*i (t ) сис-

темы n-го порядка можно представить условно в виде некоторой интеграль-

ной кривой в n–мерном пространстве с добавленной осью времени t (рис. 2.25, а). Возмущенное движение yi(t), вызванное начальным отклонением при t= t0, изображено на рис. 2.25 другой интегральной кривой.

а) б)

отклонениях xi(t), т. е. в пространстве координат состояния системы, эта кар-

тина возмущенного движения будет выглядеть, как показано на рис. 2.25, б.

При этом невозмущенное движение x*i (t ) 0 изобразится прямой линией,

совпадающей с осью t.

Невозмущенное движение системы x*i (t ) 0 называется устойчивым,

если, задав «трубку» сколь угодно малого n-мерного сечения (рис. 2.25, б), 171

можно подобрать в начальный момент t0 такую область начальных условий ,

зависящую от , что с увеличением t возмущенное движение xi(t) не выйдет из заданной трубки. Положение равновесия системы (2.250) совпадает с на-

чалом координат и может быть устойчиво, асимптотически устойчиво и не-

устойчиво.

Будем говорить, что положение устойчиво, если для любого < (рис. 2.26) существует такое , что траектория x(t), начинающаяся в точке t0

сферической области S( ), все время остается в сферической области S( ).

Иначе говоря, траектория x(t), начинающаяся внутри области S( ), ни-

когда не достигает сферы H( ).

Положение асимптотически устойчиво, если оно устойчиво и, сверх то-

го, существует такое < , что каждая траектория x(t), начинающаяся в сфе-

рической области S( ), стремится к началу координат, когда время неограни-

ченно растет.

172

2.6.3.Анализ устойчивости прямым методом Ляпунова

Основные фундаментальные результаты теории устойчивости получе-

ны русским математиком Ляпуновым А.М. (1857 – 1918 г.г.).

Заслуга А. М. Ляпунова /8/ заключается в том, что он указал подход к определению свойства устойчивости, не связанный с анализом траекторий,

т.е. дал способ, не требующий нахождения решений дифференциальных уравнений.

По существу этот подход основан на простой идее, известной из меха-

ники. В положении равновесия система имеет минимум потенциальной энер-

гии. Хорошо известно, что минимум потенциальной энергии всегда можно считать равным нулю. Тогда в любой окрестности положения равновесия ве-

личина потенциальной энергии будет положительной. Применение функций,

положительных всюду за исключением положения равновесия, к анализу ус-

тойчивости и лежит в основе метода, разработанного А. М. Ляпуновым.

Предположим, что положением равновесия системы, описываемой сис-

темой (2.250), и которое необходимо исследовать, является начало коорди-

нат, т. е. выполняются условия Xi(0, 0) = 0. Допустим, что известна некоторая функция переменных состояния V(xi), которая положительна всюду, за ис-

ключением начала координат, где она равна нулю. Такая функция показана на рис. 2.27, а; проекции сечений этой функции плоскостями V = const и по-

казаны на рис. 2.27, б /39/.

Если для любой начальной точки x0 ( x10 x20 ) функция V( x0 ) такова

что ее производная dV 0 , то траектория направлена в сторону уменьшения dt

V. Если всюду, как это показано на рис. 2.27, б, dV 0 то траектория стре- dt

мится к началу координат, которое устойчиво, в данном случае асимптотиче-

173

лю в том и только в том случае, если собственные значения i матрицы Р

(2.254), которые для симметричной матрицы действительны, соответственно все положительны, все отрицательны, все неотрицательны, все неположи-

тельны, имеют различные знаки или все равны нулю.

Собственные значения i (j= 1,2, . . ., n) матрицы Р – это корни характе-

ристического уравнения

det( E P) E P 0

или

Сформулируем еще один признак определенной положительности квадратичной формы, известный как критерий Сильвестра.

Для того чтобы квадратичная форма (2.254) была положительно опре-

деленной, необходимо и достаточно, чтобы каждый из угловых миноров

Для того чтобы проанализировать устойчивость, введем функцию Ля-

пунова в виде положительно определенной квадратичной формы (2.254).

177

Найдем производную этой функции с учетом уравнений (2.257)

системы стремится к началу координат. Итак, если одновременно выполня-

ются неравенства V >0 и V 0 в некоторой области пространства перемен-

ных (x1, . . ., xn), включающей начало координат, то положение равновесия в начале координат асимптотически устойчиво.

Согласно теореме Ляпунова об асимптотической устойчивости, для то-

го чтобы нулевое решение автономной линейной системы (2.257) было асим-

птотически устойчиво, необходимо и достаточно, чтобы для произвольной положительно определенной матрицы Q существовала положительно опре-

деленная матрица Р, удовлетворяющая уравнению (2.259). Отметим, что обе матрицы Р и Q являются симметричными. Действительно, если матрица Р симметрична, т. е. РT = Р, то

QT ( AT P PA)T PT A AT P ( AT P PA) Q

и, следовательно, матрица Q симметрична. Справедливо и обратное.

Рассмотрим теперь интерпретацию задачи определения устойчивости для системы, описываемой конечно-разностным уравнением в дискретном времени (цифровой системы)

x[k 1] f ( x[k ],k ), xk 1 fk ( xk ). (2.260)

Функция V(x[k],k)=Vk(x) является функцией Ляпунова для системы

(2.260) в случае если:

1. Vk(x) непрерывна по x и Vk(0)=0; 178

2.Vk(x) – положительно определена при x 0, Vk(x)>0;

3.Vk(x)=Vk(xk+1)-Vk(xk)=Vk(f(xk))-Vk(xk) 0 (неотрицательно определе-

на).

Теорема об устойчивости формулируется следующим образом: если для системы (2.260) существует функция Ляпунова, то решение x[k]=xk=0

асимптотически устойчиво.

Как уже упоминалось, главную трудность составляет нахождение под-

ходящей функции Ляпунова. Однако она легко определяется для линейных систем вида

xk 1 Axk , x0 a x[0 ].

Отметим, что разность x x x для другого решения

Это значит, что если xk устойчиво, то каждое другое решение также ус-

тойчиво. То есть для линейных систем устойчивость – свойство системы, а не конкретного решения.

Для линейной системы при a=0 функцию Ляпунова обычно ищут в ви-

де

Vk ( x ) xkT Bxk ,

где B – положительно определенная матрица. Вычислим первую разность функции Ляпунова и преобразуем ее к виду

Vk ( x ) xkT 1Bxk 1 xkT Bxk xkT AT BAxk xk BxkxkT ( AT AB B)xk xkTCxk

где C – некоторая положительно определенная матрица, которая находится из матричного уравнения

AT BA B C I

Это уравнение (матричное уравнение Ляпунова) всегда имеет решение,

если система устойчива. В качестве C обычно выбирают единичную матрицу

179

C=I.

Если матрицу A путем невырожденного преобразования F можно при-

вести к диагональному виду, то

и решение есть линейная комбинация ik , где i, i=1,2,…,m собственные чис-

ла матрицы A. Для достижения асимптотической устойчивости все решения должны стремиться к нулю при k . В этом случае все собственные числа матрицы А должны обладать свойством i <1. В самом простейшем случае скалярного уравнения xk+1=rxk, x0=a устойчивость достигается при r <1, так как xk+1=rkx0 и любое возмущение начального значения будет «погашено» с

течением времени.

2.7. Инвариантность и чувствительность линейных систем

автоматического управления

Инвариантность. Данное свойство динамических систем определяет степень восприимчивости одного или нескольких компонентов движения системы в фазовом пространстве x(t) от изменяющегося во времени возму-

щающего воздействия (t)

Инвариантность траектории системы (2.261) обеспечивается достаточ-

но сложно и только при наличии точной математической модели и необхо-

димого объема априорных данных. Даже для линейной стационарной систе-

мы условия инвариантности определяются на основе специальных уравнений для элементов матрицы А ( x Ax Bu C ), которые определяют условия компенсации возмущений и которые не всегда имеют решение. Порядок сис-

темы для обеспечения инвариантности должен быть не менее двух, так как в противном случае имеется ее полная неуправляемость. Более подробно ос-

новные положения теории инвариантности излагается в разделе 3.9.3.

180