
Теория определяющих соотношений. Часть 2. Теория пластичности
.pdf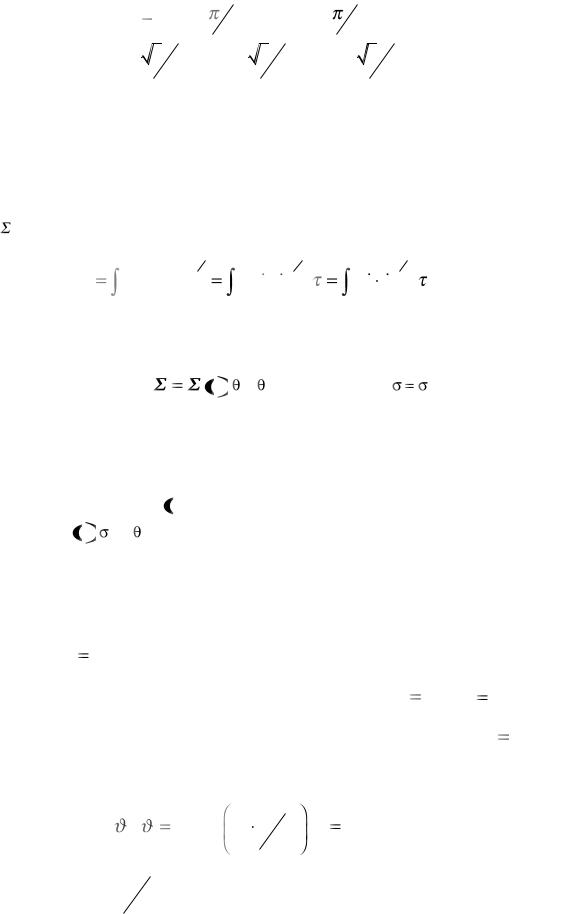
e11 = cosβ э1 + sinβ э2 , |
|
|
|
|
|
|
|||||||
e22 = |
|
sin(β + |
6 |
) э1 + cos(β + |
6 |
) э2 , |
(5.5) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e12 = |
3 |
2 э3 , |
e23 = |
3 |
2 э4 , e31 |
= |
3 |
|
э5. |
||||
|
|
|
|
2 |
|||||||||
Компоненты девиаторов S33 и е33 определяются из условия равенства нулю первых инвариантов девиаторов. Угол β определяет вращение проекции векторов напряжений (деформаций) в плоскости а1 – а2.
При произвольном процессе деформирования вектор-функция э(t) описывает в пространстве Э(5) некоторую линию, называемую траекторией деформации (годограф век- тора-функции э t ). Соответствующая вектор–функция напряжений Σ (t) в пространст-
ве (5) определяет траекторию нагружения. Длина дуги траектории деформации, отсчитываемая от начала процесса деформирования, определяется как
s |
t |
2 |
de : de |
12 |
t |
2 |
e : e |
12 |
d |
t |
э э |
12 |
d . |
(5.6) |
|
|
|
|
|
|
|||||||||
0 |
3 |
|
0 |
3 |
|
0 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Поскольку в классической теории пластичности время явным образом не должно присутствовать, обычно в качестве параметра, характеризующего течение (последовательность стадий) процесса деформирования, используется именно длина дуги траектории деформации. В этом случае полагается, что все параметры процесса определяются как функции
длины дуги s (например |
s , = (s) – температура, |
(s) – среднее напряжение |
и т.д.). В некоторых ситуациях вместо длины дуги полной деформации более целесообразно использовать длину дуги пластической деформации.
Одним из основных понятий теории УПП является понятие образа процесса нагружения, дающее весьма наглядное представление о воздействиях (деформациях) и отклике (напряжениях) материала. Образом процесса нагружения в пространстве Э(5) называется
траектория деформации э s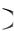 и приписанные каждой точке траектории характеристики процесса (
и приписанные каждой точке траектории характеристики процесса (  s , (s), (s) и другие). Траектория деформации полагается заданной непре-
s , (s), (s) и другие). Траектория деформации полагается заданной непре-
рывной вектор-значной функцией параметра s (или t) c непрерывными производными до пятого порядка за исключением, может быть, конечного числа точек разрыва производных.
Для компонентного представления вектора напряжений в этом случае удобно (почему – будет пояснено ниже) использовать так называемый естественный ортогональный репер
Френе pi |
|
|
|
|
|
|
|
|||
( i 1,5). Для построения пятигранника Френе используется процедура орто- |
||||||||||
гонализации системы пяти линейно независимых векторов ri |
di э |
|
|
|
|
|||||
( i |
1,5); достаточно |
|||||||||
|
||||||||||
|
|
|
|
dsi |
|
|
|
|
||
подробно процедура ортогонализации рассмотрена в [13]. Заметим, что r1 p1 |
– еди- |
|||||||||
ничный вектор, касательный к траектории, вектор r2 ортогонален p1 |
(нормаль) и ле- |
|||||||||
жит в соприкасающейся плоскости. Ориентация вектора напряжений в репере Френе оп-
|
|
i arccos p |
i |
Σ |
|
|
|
|
|
|
ределяется углами |
i : |
Σ |
|
, i 1,5 |
, из которых только четыре явля- |
|||||
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ются независимыми. Приведем известное из дифференциальной геометрии соотношение для производных dpi ds :
191

dpi |
ds |
κ pi 1 |
κ pi 1 , |
(5.7) |
|
i 1 |
i |
|
|
|
|
|
где κ0 κ5 0, κi (i = 1,4) – параметры кривизны и кручения траектории деформации,
κi2 |
|
di э |
|
di э |
|
|
|
|
|
1 |
|
, |
i 2,5. |
(5.8) |
|||||
dsi |
|
dsi |
|||||||
|
|
|
|
|
|
|
|
||
В случае задания траектории деформации параметрами кривизны и кручения функциями длины дуги траектории деформации соотношение (5.7) можно рассматривать как дифференциальное уравнение для определения репера Френе в каждой точке траектории деформации (по заданному положению в начальный момент деформирования).
об
Наиболее важной в конкретных приложениях является кривизна траектории κ1 κ . С использованием (5.7) несложно показать, что
κi2 |
κi2 |
|
|
dpi |
|
|
|
dpi |
|
|
|
|
|
1 |
|
|
|
|
, i 1,4 . |
(5.9) |
|||||||
|
ds |
|
|
|
|||||||||
|
|
|
|
|
|
|
ds |
|
|||||
В частных случаях при размерности пространства D , меньшей 5, формула используется |
|||||||||||||
только до i D 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Параметры кривизны и кручения κi |
|
|
|
|
|||||||||
( i |
1,4 ) как функции длины дуги траектории s пол- |
||||||||||||
ностью определяют внутреннюю геометрию траектории деформации (т.е. с точностью до ортогональных преобразований траектории в Э(5)). При рассмотрении плоских траекторий
с изломами в число внутренних параметров вводятся также координаты sr и углы излома
ir (углы определяются между касательными при sr 0 и sr 0 ); в общем случае необхо-
димо задавать ориентацию репера Френе справа от точки излома по отношению к реперу Френе слева от этой точки.
С использованием репера Френе вектор напряжений предста в- ляется в виде
Σ = Σ |
pi |
|
|
(5.10) |
i |
|
|
|
|
или |
|
|
|
|
Σ = Σ cos |
i |
pi , |
(5.11) |
|
|
|
|
|
|
где i (или , i ) являются функционалами кривизн κi и указанных выше параметров, характеризующих воздействия немеханической природы и среднее давление. Согласно принятой в теории УПП терминологии, говорят, что характеризует скалярные свойства,
аi – векторные свойства материала (вообще говоря – и процесса деформирования)
Отметим, что согласно принципу запаздывания (памяти) векторных свойств (более
детально принцип изложен ниже), ориентация вектора |
в репере Френе (т.е. углы i ) |
определяется не всей предысторией деформирования, а лишь предшествующим участком траектории деформации длиной h, называемым следом запаздывания. След запаздывания в теории УПП и следующих из неё частных теориях обычно полагается материальной константой, величина которого составляет 3–10 «предела текучести по деформациям» (т.е.
σs  E ) [13]. Исходя из физического рассмотрения процесса пластического деформирова-
E ) [13]. Исходя из физического рассмотрения процесса пластического деформирова-
ния, однако, можно предположить, что след запаздывания существенным образом зависит от микроструктуры материала (включая дислокационные субструктуры); т.е. след запаздывания скорее является внутренней переменной, для которой необходимо формулировать кинетическое уравнение. В рамках макрофеноменологического подхода след запаз-
192

дывания, как отмечается в [7], более правильно считать функционалом процесса. Однако в практических приложениях тем не менее h обычно полагается постоянной материала и определяется из опытов на двухзвенных [7] (или многозвенных) траекториях деформации
как длина траектории, по прошествию которой угол |
1 |
составляет принятую по соглаше- |
|
|
нию (обычно – одну десятую или одну шестнадцатую) долю от угла излома траектории.
Вводя обозначение κˆ max(κi ) , можно следующим образом классифицировать траек-
i 1,4
тории деформации: а) κˆ 0 – траектории простого нагружения (траектории деформации
– лучи, исходящие из начала координат в пространстве деформаций, векторы напряжений
и деформаций, как и их приращения, направлены вдоль этого луча); б) κˆ |
h 1 – траекто- |
|
рии малой кривизны; в) κˆ |
h 1 – траектории средней кривизны; г) κˆ |
h 1 – траектории |
большой кривизны; д) κˆ |
h 1 – траектории с изломами. |
|
Аналогичные определения и соотношения можно привести для процесса нагружения (в пространстве (5)).
Для чего же вводится представление вектора напряжений в базисе Френе? Чем это удобно? Как показывают многочисленные экспериментальные данные, для траекторий с малыми кривизнами и кручениями значащим является только первый член разложения в репере Френе, для более сложных траекторий деформации (средней кривизны, двухзвенных траекторий с изломами) нельзя пренебрегать проекцией на р2, остальные проекции оказы-
ваются существенно меньшими по величине. В исходном же базисе ai в общем случае все компоненты вектора напряжений оказываются значимыми независимо от сложности траектории деформации. Следует отметить, что в случае деформирования по траекториям произвольной сложности вопрос о малости компонент тензора напряжений при базисных векторах р2, р3, р4, р5 может быть решен только на основе анализа экспериментальных данных. Однако и в этом случае, как следует из изложенного ниже частного постулата изотропии, представление в базисе Френе предпочтительнее использования разложения в
базисе ai (вообще говоря, произвольно выбираемом).
В основу теории УПП положены [17]: постулат изотропии в общей форме (или постулат макроскопической определимости, или принцип детерминизма), постулат пластичности А.А. Ильюшина, гипотеза макрофизической определимости, принцип запаздывания.
Для формулировки отдельных определяющих соотношений в рамках теории УПП боль-
шое значение имеют частный постулат изотропии, гипотеза локальной определенно-
сти, гипотеза компланарности. Принцип детерминизма и гипотеза макрофизической определимости изложены в общей теории определяющих соотношений [62], постулат пластичности А.А. Ильюшина – в гл.4.
Одним из наиболее конструктивных для построения теории пластичности является принцип запаздывания (векторных свойств) [15, 17] (детальное изложение принципа содер-
жится в [7, 13]):
Ориентация вектора напряжений относительно репера Френе определяется не всей предысторией деформации из начального состояния, а лишь некоторым конечным участком непосредственно предшествующей (рассматриваемому моменту) траектории деформации длиной h (след запаздывания).
По существу, принцип запаздывания устанавливает затухающую память материала по векторным свойствам, в связи с чем более правильным было бы назвать его «принципом затухающей памяти векторных свойств», а h –«глубиной памяти векторных свойств, что обсуждалось еще в работе [7].
Следует отметить, что по аналогии с принципом запаздывания векторных свойств формулируется и принцип запаздывания скалярных свойств (см., например, [7]), однако при этом речь в основном идет о восстановлении скалярных свойств после, например,
193

излома траектории деформации и «нырка» интенсивности напряжений в точке излома (см. гл. 2). К сожалению, при анализе результатов макроэкспериментов ничего не говорится о микроструктуре материалов, при этом сами эксперименты проводятся для достаточно малых деформаций (порядка нескольких процентов). Как представляется, для скалярных свойств принцип запаздывания не должен выполняться, т.е. величина вектора напряжений определяется, вообще говоря, всей историей пластической деформации, что с очевидностью следует из физического рассмотрения (см. гл. 3). Следует отметить, что в большинстве работ по теории пластичности принимается гипотеза «единой кривой», согласно которой интенсивность напряжений при активном упругопластическом деформировании зависит только от накопленной пластической деформации (всей!) и не зависит от процесса деформирования. Это позволяет использовать для определения зависимости величины вектора напряжений от накопленной деформации опыты на одноосное нагружение.
Из известных экспериментальных данных о процессах деформирования в подпространствах Э(q) Э(5) , q < 5 и принципа запаздывания следует весьма важное для построения конкретных ОС следствие: Если начиная с некоторой точки А траектории деформации последняя принадлежит подпространству Э(q) Э(5) , q < 5 пространства деформаций, то начиная с некоторой точки В, отстоящей (вдоль траектории деформации) от точки А на величину следа запаздывания, вектор напряжений  принадлежит соответствующему (т.е. ориентированному аналогичным образом в совмещенном пространстве на-
принадлежит соответствующему (т.е. ориентированному аналогичным образом в совмещенном пространстве на-
пряжений и деформаций) подпространству Σ(q) Σ(5) . Другим имеющим важное практическое значение следствием является следующее [13]: на плоских траекториях деформации постоянной кривизны по истечении следа запаздывания угол между вектором на-
пряжений и касательной к траектории деформации |
1 |
становится постоянным. |
|
|
Из этих двух следствий вытекает еще одно, подтвержденное экспериментально (В.С. Ленский): при деформировании по траекториям малой кривизны вектор напряжений направлен по касательной к траектории деформации. Действительно, в этом случае каждый участок траектории длиной не менее h мало отличается от прямолинейного, для которого вектор напряжений направлен вдоль траектории.
Для начально изотропных тел достаточно хорошо эксп е- риментально обоснован постулат изотропии в частной форме :
Образ процесса нагружения инвариантен относительно ортогональных преобразований в совмещенном пространстве напряжений – деформаций.
Согласно постулату нагружение по двум траекториям дефо р- мации, внутренняя геометрия которых одинакова (в пределах тр е- буемой точности), и при одинаковых других параметрах воздейс т- вия в соответствующих точках траекторий приводит к одинаков о- му отклику (одинаковым компонентам вектора напряжений в соо т- ветствующих реперах Френе). Следует отметить, что указанный постулат едва ли удалось бы сформулировать без представления вектора напряжений вида (5.10) или (5.11). Данный постулат позволяет существенно сократить объем экспериментальных исследований для установления определяющих соотношений. Действ и- тельно, любой эксперимент на сложное нагружение эквивалентен множеству мощности континуум экспериментов по траекториям
194

деформации, получаемой из данной произвольными ортогонал ь- ными преобразованиями вращения и отражения в совмещенных пространствах напряжений и деформаций. Постулат также по д- тверждает приемлемость классификации процессов деформиров а- ния только по параметрам внутренней геометрии траекторий д е- формации.
Для дальнейшей конкретизации функциональной зависимости векторных свойств весьма конструктивной следует признать предложенную В.С. Ленским гипотезу локальной определенности.
Скорость изменения углов ориентации i определяется текущими значениями углов i , кривизн κi и длины дуги s:
|
d i |
ds |
i k |
, κk |
, s |
|
(5.12) |
|
|
|
|||||
|
|
|
|
|
|
|
|
где |
i – универсальные функции материала. |
|
|
||||
В некоторых случаях в число аргументов функций |
i |
включают модуль вектора напря- |
|||||
|
|
|
|
|
|
|
|
жений |
(или и). |
|
|
|
|
|
|
В ряде работ встречается несколько отличающаяся формулировка гипотезы локальной определенности: приращение dΣ вектора напряжений определяется его модулем и и ориентацией в текущем репере Френе, внутренней геометрией в рассматриваемой точке траектории деформации, т.е.
dΣ |
i σu , |
i |
|
ds |
k , κk , s p |
. |
|
|
|
|
В сочетании с принципом запаздывания векторных свойств гипотеза локальной определенности также дает возможность существенного сокращения объема экспериментальных исследований, необходимых для решения конкретных задач. Действительно, при наличии
конечного набора экспериментальных зависимостей i k , κk , s для принятой класси-
фикации процессов деформирования по сложности траекторий деформации, можно исследовать процессы деформирования по произвольным траекториям, конечно, при условии их удовлетворительной аппроксимации совокупностью участков траекторий, входящих в исходный набор.
Как отмечено выше, длина вектора напряжений для упрочняющихся материалов с учетом известных экспериментальных данных может считаться универсальной функцией длины
дуги траектории при активной деформации: и |
Ф s (за исключением сложных на- |
гружений, например, в окрестности точки излома имеет место «нырок» (резкое уменьшение) величины вектора напряжений); здесь и далее Ф(s) – зависимость напряжения от длины дуги деформации, полученная в опытах на одноосное нагружение.
Одним из наиболее эффективных предположений, позволяющих существенно упростить построение ОС теории пластичности, является гипотеза компланарности векто-
ров , dΣ , dэ, которая может быть записана в виде
dΣ Ndэ M Σ |
|
Σ |
|
ds , |
(5.13) |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
где N и M – функционалы процесса деформирования. В эквивалентной дифференциальной форме последнее соотношение принимает вид
dΣ |
Np1 |
M Σ |
|
|
|
. |
(5.14) |
|
|
Σ |
|
||||
ds |
|
|
|||||
|
|
|
|
|
|
195
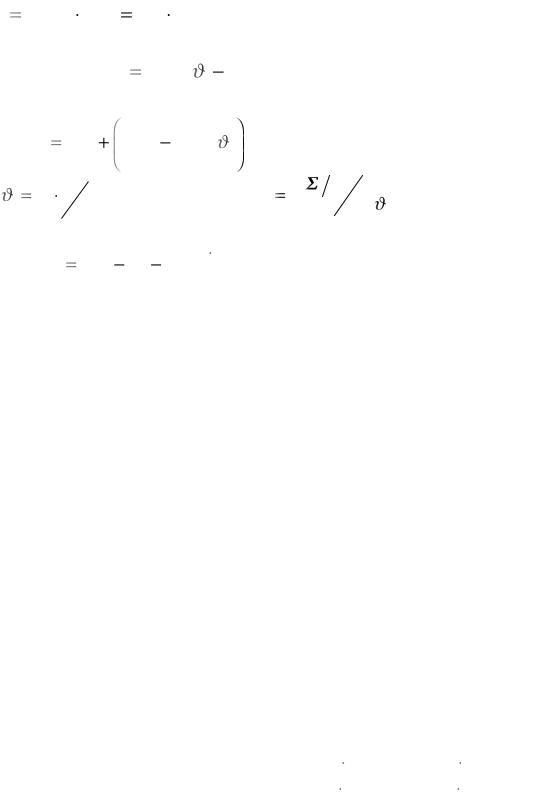
|
dΣ |
|
d |
1 |
|
|
|
|
|
||
Учитывая, что |
|
Σ Σ 2 |
|||
ds |
|
ds |
|||
|
|
|
|
||
dΣ |
|
|
Σ |
|
|
, из соотношения (5.14) следует |
ds |
|
|
Σ |
|
|
|
|
|
|
||||
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
N cos 1 |
|
dΣ |
. |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ds |
|
|
|
|
||||||||
Тогда (5.13) (или (5.14)) можно записать в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dΣ |
Np1 |
|
d |
Σ |
|
N cos |
|
|
|
|
|
Σ |
|
|
. |
|
|
|
(5.15) |
||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
ds |
|
ds |
|
|
|
Σ |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Учитывая, что cos |
1 |
Σ |
, и вводя обозначение P |
d |
|
ds |
|
||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
1 p |
|
Σ |
|
|
|
cos |
, последнее |
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
||
соотношение преобразуем к виду |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
dΣ |
|
Ndэ |
|
P N |
Σ |
|
dэ |
Σ . |
|
|
|
(5.16) |
|||||||||||||||
|
|
|
|
|
|
Σ |
|
2 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Соотношения (5.13) – (5.16) лежат в основе многих частных теорий пластичности, входящих в теорию УПП. Заметим, что соотн о- шение вида (5.16) было предложено впервые А.А. Ил ьюшиным в 1961 г. [20, с.130–162]. Подчеркнем, что соотношение (5.16), являющееся следствием (5.13), основано на гипотезе компланарн о- сти и является математической записью последней. Следует отм е- тить, что из этого соотношения не следует расположени е вектора напряжений в соприкасающейся плоскости, как это полагается в некоторых работах, посвяще нных частным теориям в рамках теории УПП.
Может возникнуть вопрос: зачем понадобился переход от до с- таточно простой исходной формы ОС (5.13) к более сложному виду (5.16)? Вероятно, это связано со следующими обстоятельств а- ми. Теория УПП является по преимуществу макрофеноменолог и- ческой, основанной на механических экспериментах. Наиболе е распространенным видом испытаний является деформирование по траекториям в виде двухзвенных ломаных. Если нижним индексом «0» обозначить векторы репера Френе на первоначальном прям о- линейном участке траектории, то из (5.16) непосредственно следуют соотношения для определения N и Р для второго прямолинейного участка траектории как функций длины дуги пластич е-
|
2 |
|
1 |
|
||
ской деформации за точкой излома [7]: |
N = |
dΣ p0 |
, |
P = |
dΣ p0 |
, |
2 |
1 |
|||||
|
|
dэ p0 |
|
|
dэ p0 |
|
весьма удобные для обработки экспериментальных данных.
Заметим, что структура соотношений (5.13) – (5.16) совпадает со структурой ОС теории пластического течения (с учетом упругих деформаций), разрешенных относительно приращений напряжений. В работе [7] показано, что соотношений известных теорий пластического течения (Прандтля–Рейсса, Прагера–Ланинга, Генки–Надаи, Кадашеви-
196

ча–Новожилова) могут быть приведены к виду (5.16) соответствующим определением параметров N и P через параметры указанных теорий. Это позволяет без существенных изменений применять весьма обширный арсенал существующих в настоящее время методов и программ, разработанных для теории течения, с приведенными здесь ОС.
Частные теории Наиболее простой является теория малых упругопластических деформаций (А.А.
Ильюшин), справедливая, строго говоря, только для случая простого нагружения. В то же время следует отметить, что теория успешно применялась и применяется для процессов деформирования по траекториям, близким к лучевым. Векторы напряжений и деформаций
в этом случае направлены вдоль одного луча в совмещенных пространствах Э(5) и (5), так что при активной деформации
Σ |
Ф(s) |
э , |
(5.17) |
||
|
э |
|
|||
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
Ф(s) определяется в экспериментах на простое (одноосное) нагружение, при разгрузке используется закон Гука в приращениях, с возможным учетом наведенной анизотропии. Несмотря на упрощенность соотношения (5.17), данная теория хорошо зарекомендовала себя при решении многих практически важных задач, однако её применение требует по крайней мере апостериорной проверки вида траектории деформации: при существенных отклонениях последней от лучевой необходимо провести решение той же задачи с использованием более сложных теорий.
Предложенная А.А. Ильюшиным теория пластичности для траекторий малой кривиз-
ны основана на известных экспериментальных данных, согласно которым p1 Σ Σ ,
откуда имеем
dэ |
|
|
Σ |
|
|
ds |
Σ dэ |
|
Σ . |
(5.18) |
|
|
Σ |
|
|
Ф s |
2 |
||||
|
|
|||||||||
|
|
|
|
|
|
|
|
|
Вторая часть соотношения (5.18) записана для приближения к стандартному виду (5.16). Область применимости теории содержится в её названии. Следует отметить, что в настоящее время теория малой кривизны является одной из наиболее широко используемых при решении технологических задач МДТТ. В то же время замечание, приведенное выше для малых упругопластических деформаций, в полной мере относится и к соотношению
(5.18).
Для процессов деформирования по траекториям средней кривизны В.И. Малым в 60–70-х годах были получены соотношения теории средней кривизны, стандартная форма которых имеет вид
Σ Σ p1 cos 1 p2 cos 2 ,
|
Σ |
|
Ф s , 1 |
|
s B s, κ1 d , |
(5.19) |
|
|
|
|
|||||
cos2 |
|
cos2 |
|
0 |
|
||
1 |
2 |
1, |
|
||||
|
|
|
|
|
|
||
где B s,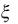 – ядро, определяемое экспериментально.
– ядро, определяемое экспериментально.
Позднее были предложены различные модификации теории средней кривизны, связанные главным образом с переходом к дифференциальной форме определяющих соотношений с введением дополнительных упрощающих гипотез. В частности, В.И. Малым в предполо-
197
жениях, что угол 1 не превышает значения |
8 ( sin 1 |
1 , cos 1 |
1), |
||||||||||
3 |
4 |
5 |
/2, т.е. вектор напряжений лежит в соприкасающейся плоскости, полу- |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
чены следующие определяющие соотношения: |
|
|
|
|
|
||||||||
|
|
|
dΣ |
Ф s |
dэ |
dФ Ф s |
|
Σ dэ |
Σ , |
(5.20) |
|||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
Ф2 s |
|||||
|
|
|
|
s |
ds |
s |
|
|
|||||
где 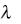 s
s – материальная функция, определяемая экспериментально. Им получено эволю-
– материальная функция, определяемая экспериментально. Им получено эволю-
ционное уравнение для угла |
1 |
|
d 1 |
ds |
κ1 |
1 |
|
. |
(5.21) |
|
|
s |
||||
|
|
|
|
|
Сопоставляя правые части (5.16) и (5.20), нетрудно видеть, что предложенное соотношение средней кривизны удовлетворяет гипотезе компланарности, при этом
N |
Ф s |
, P |
dФ ds . |
(5.22) |
s |
С.В. Ермаковым предложено обобщение (5.20), содержащее две новые материальные
функции a1 s , b1 s : |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
dΣ |
|
dФ Σ |
Ф s |
b |
b cos |
|
|
Σ |
|
|
dэ |
|
a2 a1 cos 1 |
Σ ,(5.23) |
|||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
1 Ф s ds |
|
|
||||||||
|
ds |
|
ds Ф s |
s |
2 |
1 |
|
Ф s |
|
|||||||||
a2 1 a1 , b2 1 b1 .
В варианте теории средней кривизны, разработанном Дао Зуй Биком, полагается
2
cos 1 1 1
2 . Определяющее соотношение в этом случае имеет вид
dΣ |
|
|
|
|
|
dэ |
|
dФ |
|
|
|
Σ p1 |
|
||||
|
|
|
|
|
|
||||||||||||
|
k s |
|
Σ |
|
|
|
|
|
k s |
Σ |
|
|
|
|
|
Σ , |
(5.24) |
ds |
ds |
|
ds |
|
Σ |
|
2 |
||||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где для материальной функции k s предлагается следующее аппроксимирующее выра-
жение: k s |
|
a b |
s |
, |
a |
и b – материальные постоянные. Сопоставление правых частей |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.16) и (5.24) позволяет установить следующее соответствие: |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ds |
|
dФ |
|
||||||
|
|
|
N |
|
k |
s |
|
|
s , P |
d |
Σ |
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
Σ |
|
|
|
|
cos 1 |
|
|
. |
(5.25) |
|||||||||
|
|
|
|
|
|
|
|
|
ds |
||||||||||||||
Из (5.25)2 следует: |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
s dФ |
2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
Σ |
|
s |
Ф s |
|
|
1 |
|
|
|
d , |
|
Σ |
|
0 Ф 0 . |
(5.26) |
|||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
0 ds |
|
2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Согласно полученным с использованием формулы (5.26) оценкам, максимальное отклонение 
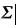 от Ф s
от Ф s составляет 7 8%. Отметим, что здесь приведены определяющие соотно-
составляет 7 8%. Отметим, что здесь приведены определяющие соотно-
шения только для участков активного пластического деформирования, разгрузка описывается обычно с помощью закона Гука.
Одной из широко используемых частных теорий является теория пластичности для траекторий в виде двухзвенных ломаных
198
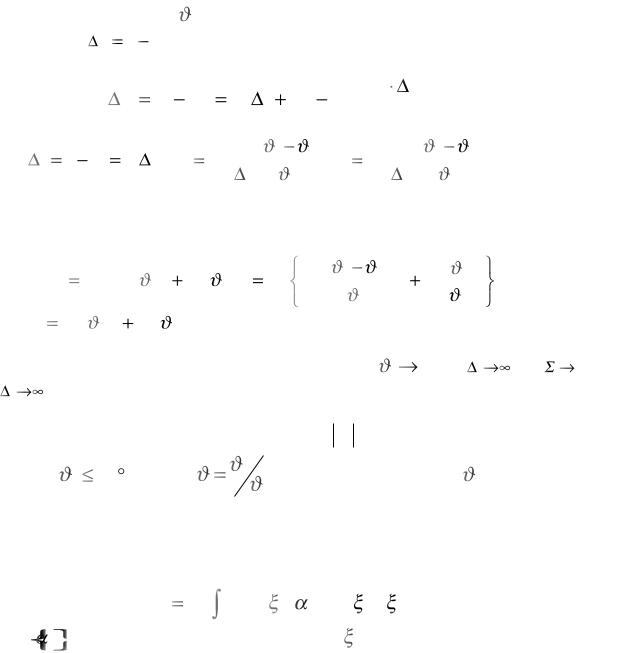
(А.А. Ильюшин, В.С. Ленский, Р.А. Васин) . Подобные процессы имеют место при потере устойчивости конструкций в упругопл а- стической области, потере устойчивости процесса упругопласт и- ческого деформирования. Существует несколько вариантов записи данных соотношений. Здесь приведены две наиболее распростр а- ненные формы.
На первом участке деформирования справедливы соотношения теории малых упругопластических деформаций. В точке излома, обозначаемой индексом «0», полагается, что вектор напряжений направлен вдоль 1-го участка траектории деформации, угол излома тра-
ектории обозначим через 0 , вектор напряжений – Σ0 , длина дуги траектории в точке излома – s0, s s s0 . Тогда в конечных приращениях определяющее соотношение может быть записано в виде (Р.А. Васин):
Σ |
Σ |
Σ |
|
|
|
|
N э |
|
P |
N |
Σ0 |
э |
Σ |
|
, |
(5.27) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
0 |
|
1 |
|
1 |
1 |
|
|
|
Σ0 |
2 |
|
0 |
|
|
|
||||
где э э э p1 |
s , |
N |
|
|
Σ |
|
sin |
0 |
1 |
, P |
|
|
Σ |
|
cos |
0 |
|
1 |
. |
|||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
0 |
|
1 |
|
|
|
|
s sin 0 |
|
1 |
|
|
|
|
|
|
s cos |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|||||
В некоторых случаях удобно использовать определя ю- щие соотношения в терминах конечных значений напряжений и деформаций (А.А. Ильюшин, В.С. Ленский):
Σ |
|
Σ |
|
cos p1 |
sin p2 |
|
Σ |
|
|
sin |
0 |
1 |
p1 |
sin |
1 |
э |
, (5.28) |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
1 |
1 |
|
|
|
|
|
sin |
|
|
sin |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
||
где э cos |
|
p1 |
sin |
p2 . |
|
|
|
|
|
|
|
|
|
|
|
|
||
0 |
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||
Из многочисленных экспериментов на двухзвенных траекториях следует, что материаль-
ные функции удовлетворяют принципу запаздывания ( 1 |
0 при s |
или 2 0 при |
|
s |
), с достаточной точностью – гипотезе локальной определенности. Сразу за точкой |
||
излома наблюдается уменьшение модуля вектора напряжений (так называемый «нырок»), после чего происходит постепенное нарастание Σ . Из экспериментов также получено,
что при 0 90 функция |
1 |
практически не зависит от |
0 ,что позволяет со- |
|
|||
|
|
0 |
|
кратить число потребных экспериментов.
В заключение отметим, что в рамках работы над теорией УПП А.А. Ильюшиным была предложена так называемая истокообразная форма определяющих соотношений [15, 16]:
|
Σ |
|
Σ |
|
s A s, |
, |
p1 |
d , |
(5.29) |
|
|
|
|||||||
|
|
|
|
|
0 |
s |
|
|
|
|
|
|
|
|
|
|
|
||
где |
означает набор параметров κn |
, κn |
, характеризующих сложность траек- |
||||||
тории предшествующей деформации. По форме приведенное соотношение близко к ОС эндохронной теории пластичности, предложенной К.Валанисом (см. гл.7), однако является более глубоким по содержанию: в отличие от последнего соотношение (5.29) имеют в своей структуре параметры, характеризующие сложность траектории деформирования. Указанное соотношение до настоящего времени не получило должного применения и развития, хотя представляется весьма перспективным.
199
Заметим, что приведенные теории пластичности имеют ярко выраженный феноменологический макроско пический характер, сформулированы на одном масштабном уровне, в связи с чем в них не присутствуют внутренние переменные в явном виде; история воздействий учитывается за счет достаточно сложных функци о- нальных зависимостей параметров процесса. Все они основа ны на хорошо поставленных, тщательно проведенных и детально проан а- лизированных экспериментах на сложное нагружение макрообра з- цов. В определенном смысле предлагаемые теории представляют собой достаточно удачную аппроксимацию результатов этих эк с- периментов. Физическая суть процессов пластического деформ и- рования не фигурирует в явном виде в обосновании предлагаемых теорий, в записи основных постулатов, гипотез и собственно ОС, она «прячется» за интуицией, накопленной в течение многих лет экспериментов и тщательного анализа полученных результатов.
В то же время авторы не разделяют существующую точку зрения, что теория УПП А.А. Ильюшина не требует никаких зн а- ний о структуре материала, что для параметров, характеризующих структуру, в ней просто нет места. В дейст вительности эти данные присутствуют в теории неявным образом, за счет указаний о хим и- ческом составе и способах предварительной обработки образцов. Если такие данные отсутствуют в статьях и отчетах об экспер и- ментальных исследованиях свойств материалов, необ ходимых для применения ОС частных теорий УПП, то использование их для решения конкретных задач не представляется возможным.
Вопросы для самопроверки
1.Запишите соотношение, связывающее первые инварианты тензора малых деформаций и тензора напряжений Коши, поясните их механический смысл.
2.Чем обусловлено широкое распространение векторного представления процесса деформирования?
3.Приведите выражения, определяющие векторы напряжений и деформаций через соответствующие компоненты девиаторов напряжений и деформаций, и обратные соотношения.
4.Дайте определения траектории деформации, траектории нагружения и образа процесса деформирования.
5.Запишите соотношение для определения длины дуги траектории деформации.
6.Каким образом осуществляется построение естественного репера Френе? С какой целью он вводится?
7.Запишите соотношения для определения параметров кривизны и кручения траектории деформации.
8.Приведите определение следа запаздывания векторных свойств. Можно ли считать величину следа запаздывания постоянной материала? Если «нет» (или «да»), то – почему?
9.Сформулируйте принцип запаздывания векторных свойств и следствия из него.
200
