
Теория определяющих соотношений. Часть 2. Теория пластичности
.pdf
будет отличной от нулевой при любом отличном от нулевого сдв и- говом напряжении K (k ) .
Эволюционное уравнение для функции упрочнения g(k ) по
структуре аналогично закону (9.1): |
|
|
g(k ) |
Hkj γ(k ) , |
(9.54) |
j
в общем случае Hij полагаются функциями накопленных сдвигов. Следуя более ранним работам Хатчинсона, Азаро и других в рассматриваемой статье используется следующее соотношение для коэффициентов матрицы упрочнения:
Hkj = HQ + (1 Q)Hδ |
kj |
, |
(9.55) |
|
|
|
где Q характеризует отношение скорости латентного упрочнения к скорости активного упрочнения. Для ГЦК -кристаллов в работе предлагается разделить 12 кристаллографических систем на 4 мн о- жества компланарных систем (по 3 в каждом множестве) . В случае принадлежности СС одному и тому же множеству Q=1.0, если же индексы k и j относятся к СС из разных множеств, то в численных экспериментах для Q принимались значения либо 1.0, либо – 1.4.
Подробно рассмотрена процедур а численного решения. Исследовалось поведение поликристаллической меди (закон распредел е- ния начальной ориентации зерен – равномерный) при растяжении и сжатии в условиях осевой симметрии и плоско -деформированного состояния. Использовались смешанные граничны е условия, объемными силами пренебрегалось, принята гипотеза Фойгта; в качестве процедуры определения осредненных напряжений для представ и- тельного объема поликристалла принято осреднение по объему. Приведены результаты расчета развития текстуры, отмечаетс я существенное влияние на её эволюцию параметра латентного упро ч- нения Q.
Представлены расчетные кривые интенсивность напряжений – интенсивность деформаций для различных значений параметра л а- тентного упрочнения. Отмечается достаточно быстрый (при
εи 0.1) выход упрочнения на уровень насыщения; дальнейший рост интенсивности напряжений при больших деформациях ( εи 0.4 ) связывается с формированием текстуры («геометрическое
упрочнение»).
Для случая комбинированного нагружения (растяжение-сжатие с одновременным сдвигом) при различных предварительных д е- формациях растяжения и сжатия построены условные «поверхности текучести» с различным допуском на неупругие деформации. Из полученных расчетных кривых видно, что предлагаемая модель к а- чественно описывает образование «носика» на «поверхности тек у- чести» в направлении нагружения, уплощение тыльной части п о- верхности, эффект Баушингера.
301

Предложенная модель с незначительными модификациями и с- пользована в [Д16] в сочетании с МКЭ для исследования локализ а- ции деформации и формирования текстуры в плоских задачах ра с- тяжения-сжатия и простого сдвига. Для установления кривых н а- пряжение–деформация в терминах компонент напряжений Кир х- гоффа и логарифмических деф ормаций в конечно–элементной модели используется определение напряжений по узловым силам на границе. Отмечается хорошее соответствие результатов, получе н- ных с помощью исходной модели Тейлора (осреднение по объему), и конечно-элементной модели для растяжени я-сжатия. Для случая простого сдвига при накопленном сдвиге конечно-
элементная модель дает заниженные (на 35%) значения нормал ь- ных напряжений по сравнению с моделью Тейлора.
Интересный вариант физической модели упруговязкопласти ч- ности предложен в работе [Д21], согласно которому монокристалл представляется совокупностью «жестких» (зоны с повышенной плотностью дислокаций, например, стенки ячеек) и «мягких» (зоны с пониженной плотностью дислокациий, например, внутренность ячеек) областей. Принимается гипотеза Фойгта; напряжения опр е- деляются суммой напряжений в «жестких» и «мягких» областях. Для каждой из областей используется изотропный закон Гука с о т- личающимися константами Ламе. Принимается гипотеза об адд и- тивном разложении тензора малых деформаций на упругую и вя з- копластическую составляющие. Неупругие деформации осущест в- ляются сдвигом в активных системах скольжения, условием акт и- вации является выполнение закона Шмида. Для каждой из областей скорости сдвигов в k- й СС определяются степенным законом вида
|
|
|
τ(k ) |
n |
|
τ(k ) |
n |
|
|
|
|
|
|
|
|
|
|||
γ(k ) = τ(k ) |
|
(S) |
sign(τ(k ) ), |
γ(k ) = |
(H) |
sign(τ(k ) ) , |
(9.56) |
||
|
τ |
|
τ(k ) |
||||||
(S) |
(S) |
|
|
(S) |
(S) |
(H) |
|
||
|
|
|
|
c0 |
|
|
c |
|
|
где индексы |
S, |
H относятся |
соответственно к «мягкой» (soft) и |
||||||
«жесткой» (hard) зонам, τc0 – постоянное критическое напряжение в «мягкой» области, τ(ck ) – критическое напряжение сдвига в «жес т-
кой» области, τ((S)k ) , τ((H)k ) – сдвиговые напряжения в k- й СС, n – показатель скоростной чувствительности. Для критического напряж е- ния сдвига в «жесткой» области τ(ck ) предлагается эволюционное
уравнение, учитывающее активное и латентное упрочнение за счет сдвигов в обеих областях и возможное разупрочнение за счет сдв и- гов в «мягкой» зоне.
Предложенная модель была использована для анализа повед е- ния монокристаллов при непропорциональном циклическом нагр у- жении (траектории деформирования – круговые, в виде квадрата, 8 -
302

лучевой звезды), отмечается удовлетворительное качественное с о- ответствие экспериментальным данным.
Встатье [Д18] рассматривается вариант упруговязкопластич е- ской модели, базирующийся на рассмотренной выше модели Asaro&Needleman [Д2]. Основное отличие заключается в использ о- вании вместо гипоупругого гиперупругого закона, в качестве меры деформации в котором принят аналог тензора Коши –Грина, а в качестве меры напряженного состояния – аналог второго тензора Пиола–Кирхгоффа, определенные в базисе разгруженной конфиг у- рации.
Вработе [Д6] рассматривается вариант упруговязкопластич е- ской модели со степенным законом течения вида (9.53) и комбинированным (изотропным и кинематическим) законом упрочнения. Используется аддитивное разложение тензоров деформации скор о- сти и вихря на упругую и неупругую составляющие
D = De + Dp , W = We + Wp . |
(9.57) |
Неупругие деформации осуществляются сдвигом (в силу чего из о- хоричны); неупругие составляющие в (9.57) определяются соотношениями (9.39) (т.е. для неупругих ротаций принимается полн о- стью стесненная модель Тейлора). Полагается, что скорость рот а- ции решетки определяется упругим спином We . В качестве ОС для упругой составляющей принимается изотропный закон Гука в ск о- ростной форме; в качестве меры скорости напряжений используе т- ся производная яуманновского типа тензора напряжений Коши
σJ = σ + σ We - We σ .
Предложенная модель встроена в конечно –элементную программу и использована для анализа образования полос сдвига в монокр и-
сталле при высокоскоростном деформировании (скорость деформ а- ции 103 с- 1 ).
В последние годы физические теории пластичности все шире применяются для решения реальных прикладных задач МДТТ. В работе [Д9] рассматривается модель пластичности кристаллов, основанная на введении тензора плотности и/или скалярной плотности дислокаций. Во втором случае предлагается использовать вязкопластический закон: при выполнении условия Шмида на некоторой системе скольжения скорость сдвига в ней определяется соотношением
|
|
|
|
nk |
|
|
|
τ(k ) - ρ(k ) |
τ(ck ) |
|
|
γ(k ) = |
|
|
|
sign(τ(k ) - τ(ck ) ) , |
(9.58) |
|
|||||
|
g(k ) |
|
|||
|
|
|
|
|
|
где τ(k ) M(k ) : σ – сдвиговое напряжение в системе скольжения k, |
M(k) – ориентаци- |
||||
онный тензор, τ(ck ) , ρ(k ) – параметры изотропного и кинематического упрочнения, зависящие от плотности дислокаций; g(k), nk – материальные константы,  X
X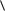
 Подробно закон упрочнения рассмотрен в [Д12] и имеет вид
Подробно закон упрочнения рассмотрен в [Д12] и имеет вид
303
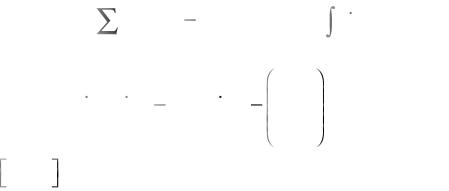
|
τ(k ) = τ(k ) + Qk h |
1 e-br γcum(r ) |
, γ(r) |
= t |
|
γ(r) |
|
dt , |
|
(9.59) |
||||||||||
|
|
|
|
|||||||||||||||||
|
c |
0 |
kr |
|
|
|
|
|
|
cum |
0 |
|
|
|
|
|
|
|||
|
|
|
r |
|
|
|
|
|
|
ρ(k ) |
|
|
mk |
|
|
|
|
|
|
|
ρ(k ) = ck αk , αk = γ(k ) |
d k αk |
|
γ(k ) |
|
|
|
|
|
sign αk |
, |
(9.60) |
|||||||||
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
Nk |
|
|
|
|
||||||||||||
|
Qk h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где матрица |
|
определяет активное и латентное упрочнение (неизотропный за- |
||||||||||||||||||
|
kr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кон упрочнения), br, dk, mk, Nk – материальные константы.
Отмечается, что в работах Флика и Хатчинсона, Фореста с соавторами данная модель расширена включением кривизн-кручений кристаллической решетки, связанных с формированием дислокационных субструктур; в законе упрочнения появляется добавочный член, пропорциональный кривизне плоскости скольжения. Отмечается существенное влияние модуля упрочнения за счет кривизны решетки на напряженнодеформированное состояние в окрестности кончика трещины в монокристалле. К сожалению, объяснений, почему кривизны-кручения должны приводить к дополнительному изотропному упрочнению, не приводится. Как представляется, более важным является появление моментных напряжений и несимметрии тензора напряжений.
В качестве примера применения физической теории для поликристаллов отмечаются результаты расчетов деформирования крупнозернистых поликристаллов. Сопоставление результатов расчета поворотов кристаллической решетки удовлетворительно согласуются с прямыми экспериментальными наблюдениями. Второй пример относится к анализу деформирования тонкого (10 мкм) цинкового покрытия стального листа, причем средний размер зерна (300 мкм) здесь существенно превышает толщину покрытия. Из результатов расчетов следует, что неоднородность деформаций присуща областям вблизи границ зерен и свободной поверхности.
При рассмотрении поликристаллов авторы выделяют три уровня:
Уровень 1 – представительный объем поликристалла, характеристиками которого служат тензоры осредненных напряжений, деформаций и некоторых внутренних переменных.
Уровень 2 – так называемая «фаза». Для химически однородных зерен под фазой понимается совокупность монокристаллов с примерно одинаковой ориентацией; для многофазных материалов (например, аустенит–феррит) под фазой понимается совокупность химически однородных монокристаллов с примерно одинаковой ориентацией. Поведение фаз описывается осредненными по указанной совокупности тензорами напряжений и деформаций. Для определения этих характеристик часто используются так называемые самосогласованные модели, например модели Крёнера или Мори–Танаки. В силу различия ориентации зерен в реальных поликристаллах в пределах фазы имеет место неоднородность (возмущения) напряжений и деформаций. Уровень, на котором эти отклонения включаются в рассмотрение, обозначается авторами как 2’.
На уровне 3, который в настоящее время реализуется с применением МКЭ, рассматриваются локальные поля напряжений и деформаций внутри зерен. Решение реальных задач описания поведения поликристаллических тел обычно ограничивается первыми двумя уровнями; для реализации подобных моделей весьма эффективными оказались параллельные вычисления, где для реализации модели на макроуровне (уровне 1) ис-
304

пользуется разделение области на подобласти с последующей «сшивкой» решения по статическим граничным условиям.
Приведены результаты решения трехмерной задачи исследования поведения поликристаллического образца сложной конфигурации, подвергнутого циклическому нагружению. Отмечается, что применение параллельных вычислений позволило более чем в семь раз сократить время вычислений по сравнению с обычной процедурой. Аналогичные результаты приведены для представительного объема поликристалла, полученные данные могут быть использованы для идентификации и верификации макрофеноменологических ОС. Для описания межзеренного разрушения вводятся соотношения, связывающие нормальные и касательные компоненты напряжений и скоростей деформаций, и эволюционное уравнение для скалярной характеристики поврежденности, при численной реализации применяются специальные граничные элементы.
К работе [Д9] вплотную примыкает статья [Д12], в которой детально рассматривается прямое конечно-элементное моделирование поведения поликристаллического агрегата с ГПУ-решеткой. Для описания зеренной структуры использовались многогранники Вороного. Исследовался агрегат из 447 зерен; в расчетах применялись разбиения на 8 8 7 , 18 18 18, 28 28 28 конечных элементов. Использовалась техника па-
раллельных вычислений с разбиением исследуемой области на блоки (число блоков – от 1 до 20). На примере одноосного растяжения показано, что для осредненных по агрегату величин кривые продольное напряжение–продольная деформация практически не отличаются для трех указанных разбиений, однако аналогичные кривые для первого и двух более детальных разбиений, построенные по осредненным напряжениям и деформациям по зернам, существенно отличаются. Результаты расчета свидетельствуют об
относительно малом разбросе осредненных по зернам напряжений, тогда как деформа-
ции имеют существенно большую дисперсию, т.е. гипотеза Тейлора об однородности полных деформаций в представительном макрообъеме не вполне справедлива. При этом результаты расчетов на мелких сетках показывают локализацию градиентов деформаций и напряжений в окрестностях границ зерен.
Проанализировано влияние на результаты расчетов используемого способа разбиения и типа конечного элемента. Отмечается, что для получения осредненных по ПО поликристалла характеристик может применяться грубая (даже один элемент на зерно) регулярная сетка с 27 точками интегрирования. Однако для описания локальных характеристик (распределения напряжений и деформаций в зерне) требуется применение сетки, адаптированной к форме зерен, и повышенный порядок аппроксимации.
Для идентификации и верификации модели рассмотрены 4 варианта растяжения с раз-
личными скоростями деформаций (от 2 10-6 до 2 10-3 с-1) и 3 варианта ползучести (при напряжениях 275, 350 и 380 МПа) образца из циркониевого сплава Zy–4 при тем-
пературе 350оС. ПО поликристалла содержал 2197 зерен, использованы разбиения 13
13 13 и 32 32 32. Во всех случаях сопоставление обнаруживает удовлетворительное соответствие теоретических и экспериментальных результатов.
Исходя из важности для процесса меж- и внутризеренного разрушения концентрации напряжений вблизи границ зерен, осуществлен детальный статистический анализ нормальных напряжений на границах зерен. Результаты его показывают, что разброс нормальных напряжений увеличивается с ростом деформации и с ростом угла между нормалью к границе и направлением растяжений.
Детальное изложение модели пластичности монокристалла содержится в работе [Д8]. Приведен общий вид условия текучести на СС:
305

τ(k ) = f (k ) (γ(k ), r(k ),θ) τ(k ) + ρ(k ) |
, |
(9.61) |
c |
|
|
где τ(k ) = σ : M(k ) напряжение сдвига в k–й системе скольжения, функция f(k) описывает вязкопластическое сопротивление сдвигу (для пластичности, не зависящей от скорости деформации, она тождественно равна нулю), θ – абсолютная температура,
r(k ) , τ(ck ) , ρ(k ) – внутренние переменные, характеризующие вязкостное (в цитируемой
статье данная составляющая называется «сопротивлением множественному скольжению», что связано с реализацией в вязкопластической модели сдвигов одновременно по всем СС), квазистатическое и кинематическое упрочнение, соответственно. Для внут-
ренних переменных r(k ) , τ(ck ) , ρ(k ) эволюционные феноменологические уравнения в общем виде записываются следующим образом:
r |
(k ) |
ˆ(k ) |
γ |
(k ) |
, r |
(k ) |
, r |
(l) |
|
|
(k ) |
|
|
(l) |
, ρ |
(k ) |
, θ , |
|
||||||||||||||||
|
|
r |
|
|
|
|
|
|
|
|
|
, τc |
,τc |
|
|
|
|
|||||||||||||||||
|
|
(k ) |
ˆ(k ) |
γ |
(k ) |
, r |
(k ) |
, r |
(l) |
(k ) |
(l) |
, ρ |
(k ) |
, θ , |
|
|||||||||||||||||||
τc |
τc |
|
|
|
|
|
|
|
|
|
, τc |
|
|
,τc |
|
|
|
(9.62) |
||||||||||||||||
ρ |
(k ) |
ˆ(k ) |
γ |
(k ) |
, r |
(k ) |
, r |
(l) |
|
(k ) |
, ρ |
(k ) |
, θ . |
|
||||||||||||||||||||
|
= ρ |
|
|
|
|
|
|
|
|
|
, τc |
|
|
|
|
|
||||||||||||||||||
Знак «^» введен для отделения функции от ее значения; наличие в 1-м и 2-м соотношении соответственно r(l ) и τ(cl ) означает учет упрочнения за счет взаимодействия дислокаций на сопряженных СС.
Формулировка конститутивной модели основана на термодинамическом подходе. Прежде всего, авторы вводят сопряженные параметрам r(k ) , τ(ck ) , ρ(k ) термодинамиче-
ские переменные состояния R(k ) , Τ (k ) , Ρ(k ) . Функция свободной энергии (Гельмгольца) представляется суммой «упругой» и «неупругой» составляющих, ψ = ψe +ψi . «Упру-
гая» составляющая зависит от тензора упругих деформаций и температуры и по ней из неравенства Клаузиуса–Дюгема определяется тензор напряжений Коши. «Неупругая» составляющая связана с внутренними переменными, определенными в СС, в связи с чем предлагается следующее представление:
|
|
ρ ψi = |
ψ(k ) +ψ(k ) +ψ(k ) |
, |
(9.63) |
||
|
|
0 |
R |
Τ |
Ρ |
|
|
|
|
|
k |
|
|
|
|
где ρ |
0 |
–плотности материала, ψ(k ) , ψ(k ) , ψ(k ) – составляющие свободной энергии на k – |
|||||
|
R |
Τ |
Ρ |
|
|
|
|
й СС, являющиеся явными функциями соответствующих термодинамических парамет-
ров состояния R(k ) , Τ (k ) , Ρ(k ) . |
Из неравенства Клаузиуса–Дюгема с учетом незави- |
||||||||||||||||||
симости термодинамических параметров состояния |
R(k ) , Τ (k ) , Ρ(k ) непосредственно |
||||||||||||||||||
следует общий вид эволюционных уравнений для r(k ) , τ(k ) |
, ρ(k ) : |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
r(k ) = ρ |
|
|
ψi |
= |
|
|
ψR(k ) |
; τ(k ) = ρ |
|
ψi |
|
= |
ψΤ(k ) |
; |
|||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
0 R(k ) |
|
|
|
|
R(k ) |
c |
0 |
Τ (k ) |
|
|
Τ (k ) |
|
||||
|
|
|
|
|
|
|
|
|
|
(9.64) |
|||||||||
|
|
|
|
|
ψi |
|
|
|
|
ψΡ(k ) |
|
|
|
|
|
|
|||
|
(k ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ρ |
|
= ρ0 |
|
|
= |
|
|
. |
|
|
|
|
|
|
|
||||
|
|
Ρ(k ) |
Ρ(k ) |
|
|
|
|
|
|
|
|||||||||
306

Далее для построения в рамках термодинамического подхода теории вязкопластичности монокристалла вводится вязкопластический потенциал
ˆ k |
(k ) |
(k ) |
(k ) |
τ |
(k ) |
, r |
(k ) |
(k) |
, ρ |
(k) |
, θ . (9.65) |
Ω = Ω |
φ |
, где φ |
= φˆ |
|
|
, τc |
|
k
С использованием вязкопластического потенциала, учитывая, что пластические деформации реализуются сдвигом по СС, получают следующее соотношение:
dp = |
Ω |
= |
|
Ω |
|
φ(k ) |
= |
γ(k )M(k ) . |
(9.66) |
σ |
k φ(k ) |
|
σ |
||||||
|
|
|
|
k |
|
||||
Суммирование в записанных выше соотношениях осуществляется по всем активным системам скольжения.
Функция диссипации определяется разностью между мощностью работы напряжений на пластических деформациях и мощности работы на квазистатическом (или вязком) и кинематическом упрочнении, чему соответствуют два представления функции диссипации:
|
p |
|
|
ψi |
|
ψΤ(l) |
(k ) |
|
|
|
|
ψi |
|
|
ψΡ(l) |
(k) |
|
|
||||||
Φ= σ :d |
|
- |
ρ0 |
|
|
|
|
Τ |
|
|
- |
|
ρ0 |
|
|
|
|
|
|
Ρ |
|
|
, |
|
|
ψ(l) |
Τ (k ) |
|
|
k |
|
ψ(l) |
|
Ρ(k ) |
|
|
|||||||||||||
|
|
k |
l |
Τ |
|
|
|
|
|
|
|
l |
|
Ρ |
|
|
|
|
|
|
|
|
|
|
(9.67) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
ψi |
|
ψR(l) |
|
(k ) |
|
|
|
|
ψi |
|
|
ψΡ(l) |
|
(k) |
|
|||||
Φ= σ :d |
|
- |
ρ0 |
|
|
|
R |
|
- |
|
ρ0 |
|
|
|
|
|
Ρ |
|
|
. |
||||
|
ψ(l) |
|
R(k ) |
|
k |
|
ψ(l) |
|
Ρ(k ) |
|
|
|||||||||||||
|
|
k |
l |
R |
|
|
|
|
|
|
|
l |
|
Ρ |
|
|
|
|
|
|
|
|
|
|
(9.68) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Относительно соотношения (9.67) необходимо отметить следующее: по сути дела, считается, что часть энергии не диссипирует, а запасается в виде внутренней энергии упругих искажений решетки, энергии взаимодействующих дислокаций, что и описывают 2-й и 3-й члены правой части. Соотношение (9.68) в этом смысле менее понятно: как правило, вязкостное трение обычно приводит к рассеянию энергии. Вероятно, в данном случае следует помнить о вязкопластичности, т.е. повышении вязкого сопротивления, которое приводит к повышению запасенной упругой энергии, реализуемой при разгрузке.
Приведенная формулировка модели, обозначаемая как ЕВ-модель (E.Busso), далее сопоставляется с другими известными соотношениями пластичности монокристаллов. В рассмотрение включены модели G.Calletaud и L.Meric e.a. (обозначенные как GC), L.Anand (LA) с соавторами, D. McDowell&R. McGinty (DM). Все указанные модели от-
носятся к классу вязкопластических, однако в рамках моделей GC и LA рассматриваются также варианты с исключением вязких членов. В табл. 9.1 и 9.2 приведена достаточно полная информация о всех соотношениях моделей. В табл. 9.1 приведены функции, описывающие вязкопластичность, выражения составляющих свободной энергии, соотношения для сопряженных термодинамических переменных, характеризующих различные виды упрочнения. Табл. 9.2 содержит сведения об эволюционных уравнениях для критического напряжения сдвига, вязкого сопротивления и остаточных микронапряжений.
Реализация всех рассматриваемых моделей осуществлялась с использованием МКЭ и неявной схемы интегрирования по времени. Сопоставление результатов расчета осуществлено для ГЦК монокристаллов (12 потенциально активных систем скольжения). Идентификация параметров модели проводилась для случая одноосного нагружения по
307
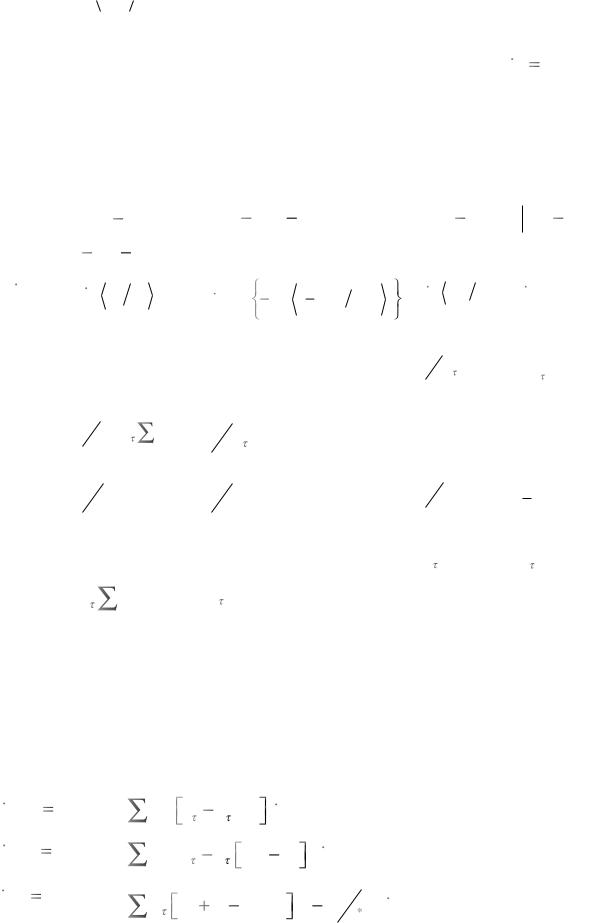
направлению  100
100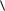 при квазистатическом нагружении и использовании закона упроч-
при квазистатическом нагружении и использовании закона упроч-
нения Тейлора. Калибровка проводилась таким образом, чтобы влияние вязкостных членов в интервале скоростей деформации 10-1–10-3 с-1было весьма малым. Во всех мо-
делях при калибровке пренебрегалось кинематическим упрочнением (т.е. ρk 0 ). Все коэффициенты моделей сведены в таблицу 9.3.
Таблица 9.1
Функции, используемые в моделях пластичности кристаллов
Функ- |
GC |
EB |
LA |
DM |
ции |
|
|
|
|
f (k) |
|
|
|
|
τ |
(k ) |
ρ |
(k ) |
|
|
||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
τ(k ) |
τ |
|
|
|
|||
|
|
|
|
|
|
|
c0 |
|
||||||
|
|
|
|
|
|
|
|
c |
|
|
|
|
||
|
γ(k ) |
|
|
γ0 f k |
τˆ |
|
|
n |
|
|||||
|
|
|
|
|
|
|||||||||
|
|
|
0 |
|
|
|||||||||
(k ) |
R |
(k |
— |
|
|
|
|
|
|
|
||||
ψˆR |
|
|
|
|
|
|
|
|
|
|
|
|||
ˆ (k ) |
|
|
(k |
1 |
|
τ(k )h |
|
|
|
|
hklT |
|||
ψT |
T |
|
|
|
2 |
c |
|
|
|
|
l |
|
||
ψˆP(k ) |
P(k |
1 |
h P(k ) |
2 |
||||||||||
|
||||||||||||||
|
|
|
|
|
|
|
2 R |
|
|
|
|
|
|
|
r(k) |
|
|
|
— |
|
|
|
|
|
|
|
|||
τc(k ) |
|
|
|
h |
|
l |
hklT (l ) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ(k ) |
|
|
|
h R(k ) |
|
|
|
|
|
|
||||
|
|
|
|
|
|
ρ |
|
|
|
|
|
|
|
|
|
τ(k ) |
ρ(k ) |
|
τ(k ) |
|
|
|
|
τ(k ) |
|
ρ(k ) |
||||||
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
q |
|
γ0 |
f |
(k ) |
r |
(k |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|||||
|
γ0 exp |
|
F |
|
1 f |
(k ) |
τˆ0 |
|
|
|
|
|
|
|
|||
|
|
kθ |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
— |
|
|
|
|
|
|
|
|
|
|
1 |
h |
|
R(k ) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
1 |
h |
T (k ) |
2 |
|
|
|
— |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
h |
P |
(k ) |
2 |
|
|
|
1 |
h |
|
P(k ) |
||||||
|
|
|
|
|
|||||||||||||
2 |
|
|
|
|
|
|
|
2 |
R |
|
|
||||||
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
— |
|
|
|
|
|
|
|
|
|
|
h R(k ) |
|
|
||||
h T |
(k ) |
|
|
|
|
|
|
|
|
|
— |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
h R(k ) |
|
|
|
|
|
|
|
|
|
h R(k ) |
|
|
|||||
|
ρ |
|
|
|
|
|
|
|
|
|
|
|
ρ |
|
|
|
|
Эволюционные уравнения для различных моделей
τ(k ) ρ(k )
γ0  f (k )
f (k )  r(k
r(k
1 |
h R(k ) |
2 |
|
||
2 |
|
|
|
|
—
12 hR P(k )
h R(k )
—
hρ R(k )
Таблица 9.2
Модель |
Уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
τc(k(GC)) |
l |
hkl |
h |
d T (l ) |
|
γ(l ) |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τc(k(EB)) |
l |
hkl |
h |
d |
τc(l ) |
|
|
τ0 |
|
γ(l ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r(LA)(k ) |
|
h |
qh |
(1 |
qh )δ |
kl |
1 |
r(l ) |
a |
|
γ |
(l ) |
|
|||
|
|
|
||||||||||||||
|
l |
|
|
|
r |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
308
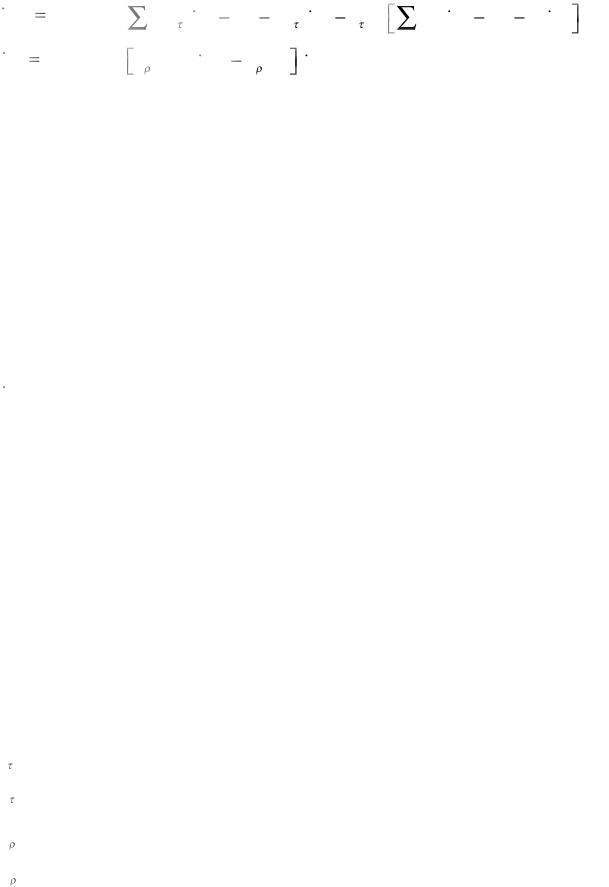
r(DM)(k ) |
|
|
|
|
|
γ(l ) |
|
d r(l ) |
|
|
γ(l ) |
|
γ(l ) |
|
||
|
q h |
γ(l ) |
(q 1)h |
|
|
|
|
q |
(q 1) |
|
||||||
|
l |
h |
|
h |
|
|
|
|
|
|
l |
h |
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ρ(k ) |
h si g n(γ(k ) ) d ρ(k ) |
|
γ(k ) |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 9.3 |
|
Материальные параметры анализируемых моделей |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
Параметр |
Параметры вязкопластических |
|
Параметры |
|
Еди- |
|
|||||||
|
|
|
моделей |
|
|
|
|
упругопластических |
ни- |
|
|||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
моделей |
|
цы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
GC |
|
EB |
LA |
DM |
|
GC |
|
LA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C11 |
|
250 |
|
250 |
250 |
250 |
|
250 |
|
250 |
ГПа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C12 |
|
200 |
|
200 |
200 |
200 |
|
200 |
|
200 |
ГПа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C44 |
|
100 |
|
100 |
100 |
100 |
|
100 |
|
100 |
ГПа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
γ0 |
|
1.0 |
|
150 |
7.3 10- |
1.0 |
|
— |
|
— |
с-1 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
2.0 |
|
— |
0.01 |
0.01 |
|
— |
|
— |
— |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ0 |
|
20 |
|
465 |
— |
— |
|
— |
|
— |
МПа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F0 |
|
— |
|
48.9 |
— |
— |
|
— |
|
— |
КДж |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
моль |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
— |
|
0.16 |
— |
— |
|
— |
|
— |
— |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
— |
|
1.22 |
— |
— |
|
— |
|
— |
— |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τc0 |
|
100 |
|
105 |
103 |
108 |
|
100 |
|
— |
МПа |
|
|
r0 |
|
|
— |
|
— |
103 |
108 |
|
— |
|
100 |
МПа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r* |
|
— |
|
— |
195 |
— |
|
— |
|
235 |
МПа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
— |
|
— |
0.929 |
— |
|
— |
|
1.6 |
— |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
1008 |
|
1150 |
1824 |
2203 |
|
1092 |
|
1953 |
МПа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
8467 |
|
12.1 |
— |
10.5 |
|
9532 |
|
— |
— |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
0.0 |
|
0.0 |
0.0 |
0.0 |
|
0.0 |
|
0.0 |
МПа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
0.0 |
|
0.0 |
0.0 |
0.0 |
|
0.0 |
|
0.0 |
— |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
kl |
, qh |
0 |
|
0 |
0 |
0 |
|
0 |
|
0 |
— |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
309

(актив- |
|
|
|
|
|
|
|
|
|
||
ное) |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
h |
kl |
, qh |
1 |
1 |
|
1 |
1 |
1 |
1 |
— |
|
|
|
|
|
|
|
|
|
|
|
||
(Тейлор) |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
Результаты расчета кривой σ |
ε при растяжении ГЦК-монокристалла в направлении [1 |
||||||||||
0 0] при скорости деформации 10-3 с-1 для всех четырех вязкопластических моделей обнаруживают удовлетворительное соответствие.
Далее анализируются результаты расчетов с использованием указанных вязкопластических моделей при двухосном деформировании монокристаллов. Кристаллографическое направление [1 0 0] совпадает во всех численных экспериментах с осью Х1. Для реализации моделей используется МКЭ (пакет Zebulon) с элементами, допускающими независимое задание нормальных и сдвиговых деформаций. Исследовались нагружения по лучевым траекториям деформации (двумерный вариант) при отношениях
ε11/ε22 |
0.95, 5.0,5.33 и ε11/ε12 0.02,0.40 (при неизменной скорости деформа- |
ции ε |
10 2 с-1 во всех вариантах). |
11 |
|
Опыты на двухосное растяжение–сжатие осуществлялись при использовании изотропного закона упрочнения Тейлора ( hkl = qh 1.0 ), сопоставление проведено для траекторий напряжений σ11 σ22 . Результаты расчетов по всем четырем моделям находятся в удовлетворительном соответствии. Рассмотрена также активация систем скольжения и
накопленный на них сдвиг. Для варианта ε11/ε22 |
5.33 отмечается, что при напряже- |
|
нии σ11 250 МПа из множества СС 1 1 1 |
1 1 0 активировались четыре первич- |
|
ные системы скольжения, а при напряжении |
σ11 |
310 МПа – дополнительно четыре |
вторичные СС. |
|
|
В экспериментах на растяжение–сдвиг использовались оба закона упрочнения – Тейлора
и деформационного ( hkl = q |
0.0 ). Здесь отмечается существенное отличие результа- |
h |
|
тов, полученных, с одной стороны, с помощью моделей EB и GC, с другой – LA и DM; в двух последних при напряжениях σ11 21 МПа и 35 МПа соответственно резко акти-
визировались вторичные СС. Данное обстоятельство связано с тем, что в моделях LA и DM учтен разворот кристаллической решетки, что отсутствует в моделях EB и GC. Для проверки этой гипотезы были проведены расчеты с использованием модели DM, в которой были отключены повороты; результаты оказались близки к результатам моделей EB и GC. Сопоставлялись также накопленные сдвиги, результаты аналогичны: близость данных по моделям EB и GC и их резкое отличие от полученных с помощью моделей LA и DM. Отмечается также, что возможным источником различия результатов являются использованные в моделях различные схемы решения нелинейных уравнений, основанные на методе Ньютона–Рафсона (Ньютона–Канторовича). Исследованию данного вопроса авторы собираются посвятить будущие работы.
Аналогичное сопоставление осуществлено для всех пяти программ нагружения при использовании упругопластических моделей LA и GC. Во всех расчетах принят закон уп-
рочнения Тейлора ( hkl = q |
1.0, ρ(k ) 0 ). Для случая двухосного растяжения–сжатия |
h |
|
траектории нагружения σ11 |
σ22 оказываются близкими; кроме того, обнаруживается |
их малое отличие от траекторий, полученных с помощью вязкопластических моделей
310
