Теория определяющих соотношений. Часть 2. Теория пластичности

шений. Например, приращение напряжений (с точностью до знака) при приращении деформации dэ, по сути дела, одинаково как для активного деформирования (Σ·dэ>0), так и для пассивного деформирования (Σ·dэ<0). С физической точки зрения подобный факт представляется необъяснимым.

В работе [52] на основе разложения общего функционала пластичности (истокообразной формы ОС) в ряд Фреше–Вольтерра показано, что рассмотренный первоначальный вариант ЭТП с достаточной точностью может быть использован для описания процессов деформирования по траекториям кривизны не выше средней. Более сложные траектории (например, большой кривизны или с изломами) описываются соотношениями (7.1)–(7.3) лишь приближенно. Иначе говоря, несоответствие экспериментальных и теоретических данных являются не следствием неверно определенных материальных констант или неверным набором экспериментов, а внутренне присуще рассматриваемым определяющим соотношениям. В силу этого первоначальный вариант ЭТП был подвергнут основательной критике в многочисленных публикациях, что побудило приверженцев ЭТП (включая ее автора) к созданию «исправленных вариантов» ЭТП. При этом наметились два основных пути «ревизии» теории: 1) изменение вида ОС ЭТП; 2) изменение определения внутреннего времени.

Одним из возможных подходов, отмеченных в [27, 53], является усложнение вида функционала (подход в рамках первого направления модификации ЭТП), представление его в виде суммы кратных интегралов по внутреннему времени (например, для описания процессов деформирования с кривизной, большей средней, требуется включение в (7.1) добавочного члена – тройного интеграла по внутреннему времени). Естественно, это приводит к необходимости определения дополнительного ядра для второго интегрального члена (содержащего уже четыре параметра), что связано с труднопреодолимыми сложностями (прежде всего – экспериментальными исследованиями; однако и использование подобных соотношений при постановке и решении конкретных краевых задач существенно усложняется).

К этому же пути относится другой вариант модификации ЭТП, предложенный Ю.И. Кадашевичем и А.Н. Михайловым [24]. В цитируемой рабо-

те предлагается так называемое тензорно-параметрическое представление

определяющего функционала

0

Здесь используется вспомогательный вектор R, играющий роль параметра. В цитируемой статье данный параметр детально не обсуждается, отсутствует его конкретное определение; отмечается только, что этот вектор характеризует влияние микродеформаций (микронапряжений) (см. гл. 6) на

231

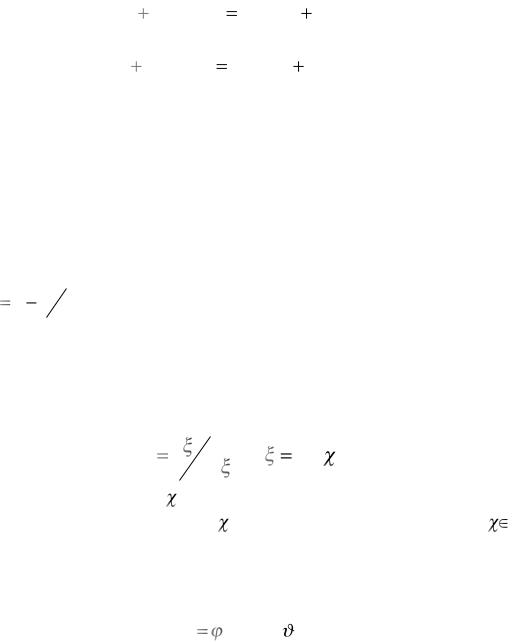
процесс упругопластического деформирования (в смысле деформирования представительного макрообъема). Введение двух ядер L1 и L2 вместо одного в первоначальном варианте ЭТП позволяет существенно расширить возможности теории (увеличить «число степеней свободы»), однако делает ее более сложной.

В цитируемой выше статье на основе анализа соотношений теории пластического течения и использования понятия микродеформаций (микронапряжений) предлагается дифференциальная форма тензорнопараметрических ОС вида

Особо подчеркивается, что (7.5) коренным образом отличаются от ОС теории пластического течения тем, что они справедливы при любой истории деформирования, как при активном нагружении, так и при разгрузке. Определение функций ai(z), bi(z), ci(z) (i=1,2) требует проведения экспериментов на сложное нагружение. Как отмечается в [52], дифференциальная форма параметрических ОС более удобна для практических расчетов.

В рамках приведенной модификации ЭТП остается открытым вопрос об определении вспомогательного вектора R. В ряде работ в качестве последнего предлагается использовать вектор пластических деформаций

эp э Σ 2G .

Другое направление модифицирования ЭТП связано с изменением меры внутреннего времени при сохранении исходной структуры уравнений. Одним из первых модификацию такого типа предложил автор теории К. Валанис [89], введя новую меру внутреннего времени следующими соотношениями:

Другой вариант изменения меры внутреннего времени был предложен А.Б. Мосоловым (1980 г.). Им была введена явная зависимость меры внутреннего времени от геометрических характеристик процесса деформирова-

232

ментально; сложность нагружения в определении (7.7) учитывается неявным образом за счет введения угла 1 .

Применение предложенной К. Валанисом новой меры внутреннего времени (7.6) позволило существенно улучшить соответствие экспериментальных и теоретических результатов. Однако и данный вариант ЭТП не освободился от недостатков первоначальной формулировки теории. К числу последних относятся нарушение постулатов Драккера и Ильюшина, появ-

ление в теоретических результатах не свойственных классической теории пластичности эффектов циклической ползучести и релаксации напряжений (как отмечается в [41], последнее следует скорее отнести к достоинствам теории, поскольку указанные эффекты действительно наблюдаются в экспериментах). В попытках избежать этих недостатков в значительном числе работ стали полагать параметр равным единице. Однако, как показано в ряде работ (см., например, [53, 89, 90, 92] и др.), это привело к возникновению сингулярности в соотношениях и появлению в теории поверхности текучести. Сингулярность ядра очевидна в силу необходимости отличия вектора напряжений от нулевого в области упругих деформаций (при равенстве нулю введенной меры внутреннего времени). Поверхность текучести в цитируемых работах определена в предположении несингулярности ядра как геометрическое место точек Σ при стремлении 0 при = 1. Как отмечается в

[53], теория тем самым лишается исходных преимуществ, декларированных при ее формулировке с самого начала. Следует отметить, что автор теории считал допустимым появление в теории поверхности текучести, однако как следствие исходных соотношений, а не постулируемого с самого начала утверждения о существовании такой поверхности (см., например, [92]). В упомянутых работах показано также, что в данном случае ОС ЭТП преобразуются к соотношениям одноповерхностной теории пластического течения с комбинированным упрочнением с интегральным законом изменения тензора внутренних микронапряжений. Приведенное выше исходное соотношение в работах К. Валаниса [89, 90 и др.] и его последователей было заменено на следующее (в терминах девиаторов напряжений и деформаций):

de – dS/ 2G – девиатор бесконечно малых приращений пластических деформаций, dz = dsp / f (sp) – внутреннее время, sp – длина дуги пластической деформации. Нетрудно видеть, что в данное соотношение с самого начала входит и предел текучести, и пластические деформации.

Последнее соотношение может быть легко преобразовано к виду соотношений теории течения с комбинированным законом упрочнения:

233

Первое из этих соотношений описывает поверхность текучести при использовании критерия Мизеса и комбинированного закона упрочнения, второе имеет следствием закон Гука (при равенстве нулевому тензору dер). По существу, полученные соотношения отличаются от уравнений одноповерхностных теорий течения (см. гл.6) только видом уравнения для тензора остаточных микронапряжений.

Представляется целесообразным остановиться более детально на посылках ЭТП и её модификаций, предложенных К. Валанисом и его последователями. Исходным пунктом построения эндохронной теории является основанное на рассмотрении экспериментальных данных утверждение о трудности (даже невозможности) определения поверхности текучести, наблюдающихся отклонениях от линейного закона Гука связях напряжение– деформация при весьма малых нагрузках (см. гл.2). В связи с этим утверждается, что размеры поверхности текучести будут тем меньше, чем точнее будут производиться измерения. В то же время в анализируемых работах [89, 90, 92, 93, 99 и др.] без всякого обсуждения используется аддитивное разло-

жение вида dε = dεe + dεp , причем для dεe используется линейный закон Гука для любых значений напряжений и произвольных процессах нагружения. Как представляется, между этими предположениями – возможностью аддитивного разложения в сочетании с применимостью закона Гука для упругих составляющих и существованием поверхности текучести (ограничивающей область применимости закона Гука в пространстве напряжений) существует тесная связь, одно не может существовать без другого. В связи с вышесказанным появление в ЭТП поверхности текучести и приводимость соотношений ЭТП к определяющим соотношениям теории пластического течения является вполне закономерным фактом.

Обратимся к анализу физического смысла параметра , проведенного впервые Ю.И. Кадашевичем и А.Б. Мосоловым [25]; изложение следует в ос-

234

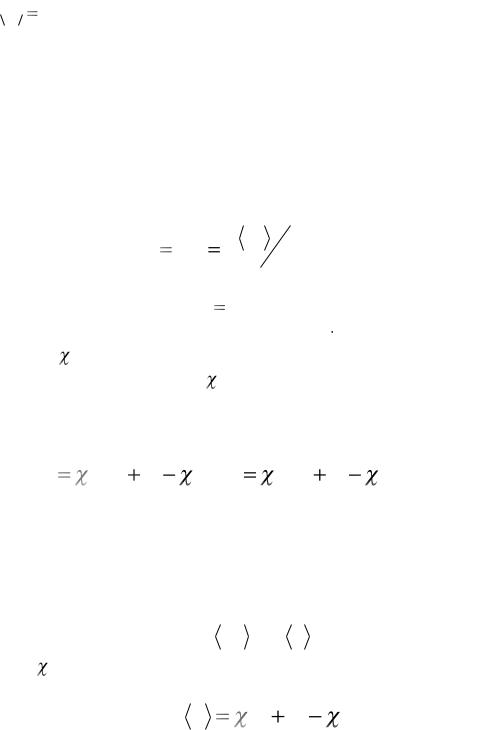
новном работе [53]. В основу анализа положен один из способов замыкания определяющих соотношений, используемый в статистической теории пластичности (см. гл.6).

Рассматривается представительный (в макросмысле) объем поликристаллического материала, состоящий из большого числа монокристаллов («зерен»). В пределах каждого из зерен напряженно-деформированное состояние (микронапряжения и микродеформации) считается однородным (т.е. рассматриваются «области однородности», введенные в квазистатистической теории (см. гл. 6)). Кроме того, принимается гипотеза Рейсса, согласно которой σ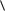 σ . Полагается, что каждое из зерен находится либо в упругом,

либо в неупругом состоянии. Следует отметить, что, вообще говоря, здесь неявным образом вводится критерий упругого (или неупругого) поведения материала на микроуровне. В цитируемом источнике, к сожалению, не рассматривается данный вопрос. В то же время указанный критерий, по существу, является аналогом поверхности текучести на микроуровне, что несколько нарушает последовательность теории в части «отсутствия в ней поверхности текучести».

Для элемента, находящегося в упругом состоянии, приращение деформаций

ском состоянии. Далее, следуя уже используемой схеме, представляется естественным определить осредненное значение приращения деформаций dэ соотношением

d 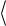э dэe 1 dэp dэe 1 dR . (7.10)

Говоря о схеме, имеем в виду структурно-механическая модель на микроуровне: по существу, модель Рейсса предполагает линейную цепочку элементов с различными физико-механическими характеристиками. Понятно, что в такой модели напряжения в каждом элементе одинаковы, а деформация определяется суммой деформаций элементов. Отметим также, что здесь принимается справедливым правило коммуникативности оператора ос-

235

в общем случае, при const, последнее соотношение, конечно, не эквива-

лентно (7.10).

Отметим, что в реальных материалах упругие и неупругие микродеформации связаны друг с другом. В данном случае это следует из самой структурной схемы: напряжения в неупругих элементах, очевидно, зависят от истории изменения неупругих деформаций. В силу принятой структурной схемы напряжения Σ в агрегате из упругих и неупругих элементов в каж-

дый момент деформирования одинаковы и, таким образом, зависят от исто-

эe ~ R в общем случае неизвестен. В качестве простейшей формы подобного

мени (7.13), соответствующей (7.6). Однако здесь параметр имеет ясно выраженный физический смысл – в каждый момент деформирования определяет вероятность реализации упругого состояния.

Отметим, что широко используемому варианту =1 отвечает предельный случай 1 (случай точного равенства =1 отвечает отсутствию пластических деформаций); согласно приведенной интерпретации параметра ситуации 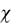1 соответствует нахождение почти всех элементов в упругом состоянии. В этом случае пластическая деформация локализуется в незначительном числе микроэлементов. Подобная ситуация действительно возникает в некоторых процессах деформирования, о чем свидетельствуют экспериментальные данные по микроструктуре. Однако в общем случае деформирова-

236

ния, особенно при сложных траекториях деформации, в пластическое деформирование оказывается вовлеченной значительная доля материала. Иначе говоря, предположение =1 не имеет достаточного обоснования с позиций физики неупругого деформирования.

В статье [32] проведен тщательный анализ ОС ЭТП с мерой (7.6); под-

обнаруженные (О.Г. Рыбакина) эффекты псевдоползучести и псевдорелаксации; авторы рекомендуют считать случай 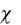1 основным рабочим вариан-

том эндохронной теории при малых деформациях, особенно при циклических нагружениях.

Другой крайний случай (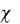 0) соответствует ситуации, когда почти все микроэлементы находятся в пластическом состоянии. При использовании понятия поверхности текучести данная ситуация имеет место при стремлении к нулю радиуса поверхностей текучести микроэлементов, что, в свою очередь, отвечает стремлению к нулю допуска на пластические деформации.

Более сложные варианты ОС ЭТП, основанные на статистическом подходе, интересующийся читатель найдет в [53].

В общем случае реалистичным следует признать значение в интервале [0,1]. При этом значение в рамках предложенной интерпретации суще-

ственно зависит от субструктуры дефектов кристаллической решетки, в

силу чего можно с полным основанием отнести к явным внутренним переменным. Поскольку микроструктура претерпевает значительные изменения в процессе пластического деформирования, то и параметр должен зависеть от истории деформирования. В рамках макроскопической теории эта зависимость должна носить, вообще говоря, функциональный характер. В общем виде такое соотношение может быть представлено следующим образом:

o

где, как обычно, rt – история градиента места (история деформирования), θt – история изменения температуры, αt – история изменения воздействий немеханической природы. Вероятно, первый вариант учета зависимости от процесса деформирования был предложен в работах А.Б. Мосолова (1980 г.), где принималось следующее соотношение:

в приведенном соотношении – функция (а не функционал) аргументов, однако зависимость от истории входит опосредованно, через зависимость угла

1 от предыстории деформации.

237

ЭТП можно отнести к феноменологическим макроскопическим тео-

риям. В связи с этим следует отметить необходимость разработки программ и проведения экспериментов на сложное нагружение. Подробно указанные проблемы рассматриваются в работах [27, 53, 90]. Заметим, что как в исходной работе [87, 88], так и в ряде последующих [89, 90, 92] декларировалось построение ОС ЭТП на основе неравновесной термодинамики, однако последняя использована только для получения весьма общей формы ОС, конкретный вид ядер функционалов и меры внутреннего времени определен феноменологически.

Остановимся на некоторых направлениях развития и применения ЭТП. Отметим, что с момента своего возникновения ЭТП предназначалась для описания процессов сложного нагружения (что является целью и большинства других созданных и создаваемых теорий пластичности); работа в этом направлении велась и ведется весьма интенсивно [43, 44, 45, 54, 98]. Особое внимание уделяется модификациям ОС ЭТП для описания простого («пропорционального») [90, 92, 93, 99] и сложного («непропорционального») [4, 41, 42] циклического нагружения. Достаточно подробный обзор работ по ЭТП с 1971 по 1990 гг. содержится в статье [27].

Как отмечено выше, в значительном числе работ по ЭТП в качестве ядра интегрального соотношения используется ядро, принятое в обобщенной модели Максвелла (7.3). Напомним, что соотношения Максвелла с ядром (7.3) соответствует многоэлементной модели с конечным набором (спектром) времен релаксации. Использование данной модели в линейной вязкоупругости не вызывает затруднений, поскольку в этом случае в качестве аргумента принимается единое для всех элементов физическое время t.

При применении обобщенной модели Максвелла в многоэлементной ЭТП естественно принять для каждого из этих структурных элементов свое внутреннее время. Ядро определяющего функционала имеет в этом случае вид

Можно ввести структурно-механическую модель многоэлементной ЭТП, состоящую из N параллельно соединенных элементов, описываемых ЭТП со своими материальными константами и внутренним временем.

Количество элементов зависит от требуемой точности теории и сложности исследуемых процессов деформирования. В пределе можно перейти к бесконечному числу элементов с некоторым статистическим распределением спектра внутреннего времени. Пусть h – некоторый параметр, определяющий спектр внутреннего времени, (h) – функция плотности распределения параметра h. Функционал ЭТП в этом случае может быть записан в виде

238

По существу, указанные соотношения можно использовать взамен соотношений ТПТ в квазистатистическом подходе, рассмотренном в предыдущем разделе, без существенного изменения структуры теории.

Представляется необходимым отметить еще одно направление развития ЭТП, связанное с учетом временных эффектов (связанных с физическим временем)[23, 26, 77, 95 и др.]. В классической теории пластичности постоянно подчеркивается, что физическое время в этой теории не должно входить в определяющие соотношения. В то же время невозможно игнорировать тот факт, что процессы неупругого деформирования происходят одновременно по нескольким (вероятно, многим) физическим механизмам, для ряда из которых физическое время является существенным параметром. Отделить деформирование по различным физическим механизмам практически невозможно, можно говорить только о преобладании, лидирующей роли одних по сравнению с другими в определенных диапазонах воздействий. При этом следует иметь в виду, что малый вклад того или иного механизма в собственно процесс деформирования (изменения конфигурации представительного объема в макросмысле) не говорит еще о его малой роли в целом, поскольку данный механизм может играть роль аккомодационного, существенно влияющего на лидирующие механизмы неупругого деформирования. О важной роли временных эффектов говорят и результаты макроэкспериментов, проведенных в последние годы. Эксперименты обнаруживают важную роль временных эффектов даже при комнатной температуре в широком интервале скоростей деформирования (10-8…101) с-1, в особенности – при сложном нагружении. Вышесказанное определяет интерес к временным эффектам и попытке их включения в ЭТП, предпринимаемые особенно интенсивно в последние десятилетия.

Следует отметить, что структура соотношений ЭТП позволяет без особых сложностей учесть указанные эффекты. Данное обстоятельство использовал создатель ЭТП К. Валанис, предложивший меру внутреннего времени,

Позднее были предложены другие варианты учета временных эффектов, как за счет изменения вида определяющего функционала, так и за счет введения других мер внутреннего времени. Так, например, Охаши предложил следующую меру:

239

Как уже отмечалось выше, в ЭТП вообще не требуется наличие единой меры внутреннего времени. Например, в многоэлементных вариантах ЭТП для ряда элементов можно вводить меры, связанные с физическим временем; можно рассмотреть модели, имеющие непрерывный спектр, содержащий физическое время.

Весьма интенсивно развивается направление, связанное с описанием в рамках ЭТП накопления поврежденности и разрушения [31, 69, 75, 91, 96, 100 и др.]. Большинство работ данного направления основаны на линейной неравновесной термодинамике, в рамках которой вводятся внутренние переменные, отвечающие за поврежденность и необратимые деформации. Далее вводятся определения функции свободной энергии и диссипативной функции; соотношения конститутивной модели формулируются, как правило, на основе неравенства Клаузиуса–Дюгема.

Несмотря на то, что настоящее пособие посвящено теориям пластичности при малых деформациях (так называемым геометрически линейным теориям), следует кратко упомянуть работы, посвященные еще одному направлению развития ЭТП, связанному с описанием процессов деформирования при больших пластических деформациях. Заметим, что в большинстве работ по геометрически нелинейным теориям используется термин «конечные деформации», который не представляется достаточно точно отражающим суть вопроса – «малые» деформации также являются конечными; более корректно следует пользоваться термином «большие градиенты перемещений», поскольку даже в случае малых удлинений материальных волокон и малых искажений углов между ними большие повороты материальных частиц как целого ведут к неприемлемости геометрически линейных ОС [57]. Особенно интенсивно указанное направление развивается в последнее десятилетие [33, 34, 97 и др.].

При построении геометрически нелинейных ОС исследователи сталкиваются с несколькими проблемами, к числу наиболее часто отмечаемых относятся выбор мер напряженного и деформированного состояния и их скоростей, выполнение принципа независимости от выбора системы отсчета (принципа материальной индифферентности) [61, 62]. В качестве исходных принимаются известные геометрически линейные ОС, как правило – записанные в дифференциальной форме. Аналогичным путем шли и авторы работ[33, 34, 97], используя в качестве отправной точки различные варианты геометрически линейных ОС ЭТП. Для удовлетворения принципу материальной индифферентности применяется переход к мерам напряжений и деформаций и их скоростей, инвариантным по отношению к наложенному жесткому движению [61, 62]. К сожалению, в цитируемых выше работах, как и в подавляющем большинстве исследований, посвященных построению геометрически нелинейных ОС упругопластических тел, практически не обсуждается одна из наиболее остро стоящих проблем – корректное разложение движения на квазитвердое и деформационное [57].

240