
Теория определяющих соотношений. Часть 2. Теория пластичности
.pdf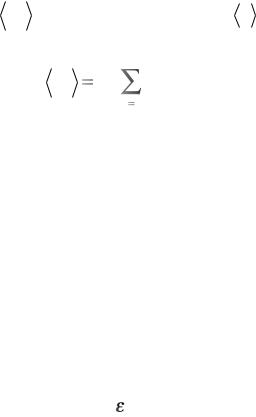
Основы рассматриваемого подхода были заложены в работах Г. Мазинга, Е. Кренера, А.Ю. Ишлинского, Н.Н. Афанасьева, В.В. Новожилова. Отметим, что статистический подход используется не только в теории пластичности – в равной степени он применим в теориях ползучести, вязкоупругости, разрушения и других. Изложение применения подхода в теории пластичности отнесено к разделу теории пластического течения только в связи с тем, что здесь рассматривается вариант статистической теории, использующий во многом схему построения соотношений ТПТ. В то же время статистический подход может быть использован для построения определяющих соотношений, существенно отличающихся от уравнений ТПТ, например для соотношений типа частных теорий в рамках теории УПП А.А. Ильюшина.
Будет рассматриваться поликристаллический материал, представляемый совокупностью монокристаллических микроэлементов (зерен, субзерен). Каждый из микроэлементов обладает анизотропией как упругих, так и пластических свойств, а также неодинаковой (с другими элементами) плотностью и конфигурацией дефектов, в основном отвечающих за процессы неупругого деформирования (см. гл. 3). Указанные обстоятельства предопределяют неравномерность пластических деформаций зерен, образующих область выбранного представительного макрообъема (в инженерном смысле, или в макросмысле).
Для представительного объема поликристаллического тела, состоящего из N «областей однородности» (т.е. совокупностей монокристаллов (зерен, субзерен, фрагментов) с примерно одинаковыми свойствами, примерно однородными деформациями и напряжениями) вводится осредненная пласти-
ческая деформация εp (здесь и далее значком |
обозначаются осреднен- |
||||
ные величины): |
|
|
|
|
|
εp |
1 N |
ε(k )p , |
(6.24) |
||
|
|
||||
N k |
|||||
|
1 |
|
|||
где ε(k )p – деформация k-й области (вообще говоря, также являющаяся некоторой осредненной по группе монокристаллов, входящих в «область однородности»). Отметим, что k-я область полагается состоящей из микрообъемов, в общем случае не контактирующих друг с другом, но имеющих примерно одинаковые пластические деформации. Обычно области нумеруются в порядке возрастания соответствующих пределов текучести (в случае изотропного упрочнения или некоторой интегральной характеристики текучести при анизотропном упрочнении). Допускается совпадение пределов текучести в нескольких областях, что позволяет учесть статистическое распределение пределов текучести, не вводя в (6.24) весовые коэффициенты, характеризующие вероятность распределения «областей однородности» по пределу текучести.
Соотношения типа (6.24) можно записать отдельно для шаровых и девиаторных составляющих тензора p :
221
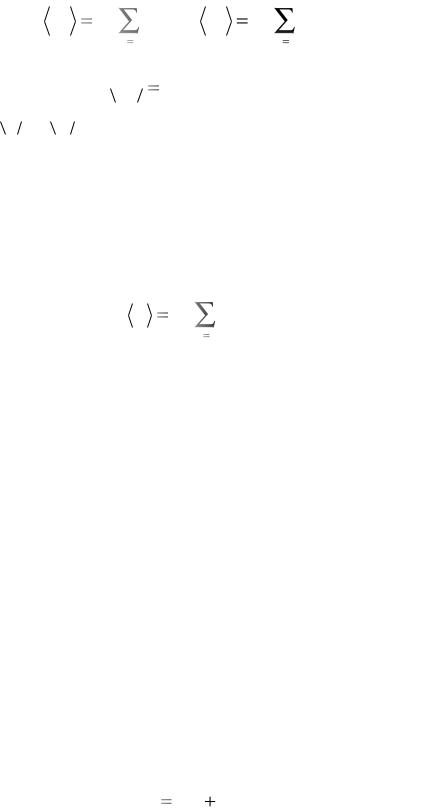
εp |
1 N |
ε(k )p , ep |
1 N |
e(k )p . |
(6.25) |
|||
|
|
|
|
|||||
N k 1 |
N k |
|||||||
|
|
1 |
|
|||||
Обычно для каждой из областей принимается предположение о пластической несжимаемости, откуда  εp
εp  0 . Принимая в дальнейшем гипотезу о линей-
0 . Принимая в дальнейшем гипотезу о линей-
ной связи  ε
ε и
и  σ
σ , будем оперировать только с девиаторными составляю-
, будем оперировать только с девиаторными составляю-
щими тензоров напряжений и деформаций.
Для каждой из областей в текущий момент нагружения проверяется условие текучести; при его выполнении приращения пластических деформаций в соответствующей области будут ненулевыми, в противном случае пластические деформации неизменны.
Аналогично деформациям определяются средние девиаторы напряжений для представительного объема:
S |
1 N |
S(k ) , |
(6.26) |
||
|
|
||||
N k |
|||||
|
1 |
|
|||
где S(k ) – средние девиаторы в тех же областях (одинаковых пределов текучести и пластических деформаций).
Из многочисленных экспериментов известно, что при пластическом деформировании не вся энергия, затраченная на деформирование, переходит в тепловую энергию (диссипирует), часть энергии сохраняется в деформи-
рованном теле в виде потенциальной («запасенной» упругой) энергии
(см. выше и гл.3). Механизм накопления этой энергии связан с неоднородностью пластического деформирования и несовместностью упругих и пластических составляющих (по отдельности) тензора деформаций, хотя полные деформации в случае сохранения сплошности являются совместными. Отметим, что речь здесь идет о пластических и упругих деформациях, одинаковых в «областях однородности», но отличающихся от области к области; в рамках рассматриваемого подхода указанные деформации отнесены к микродеформациям.
По аналогии с феноменологическими (одноповерхностными) макроскопическими теориями течения можно предположить, что появление добавочной потенциальной энергии (на микроуровне в принятом смысле) связано с появлением добавочных упругих микронапряжений. Тогда девиатор напря-
жений S(k ) в k-й области можно представить совокупностью диссипативной τ(k ) и упругой ρ(k ) составляющих:
S(k ) τ(k ) ρ(k ) . |
(6.27) |
Для упругих напряжений предполагается, как обычно, что их работа на любом замкнутом цикле деформаций равна нулю, в частности, на любых замкнутых циклах пластической деформации. Отсюда следует наличие потенциала упругих напряжений, т.е. существование скалярной функции пластических деформаций (поскольку именно несовместность пластических деформаций является источником возникновения несовместных упругих де-
222
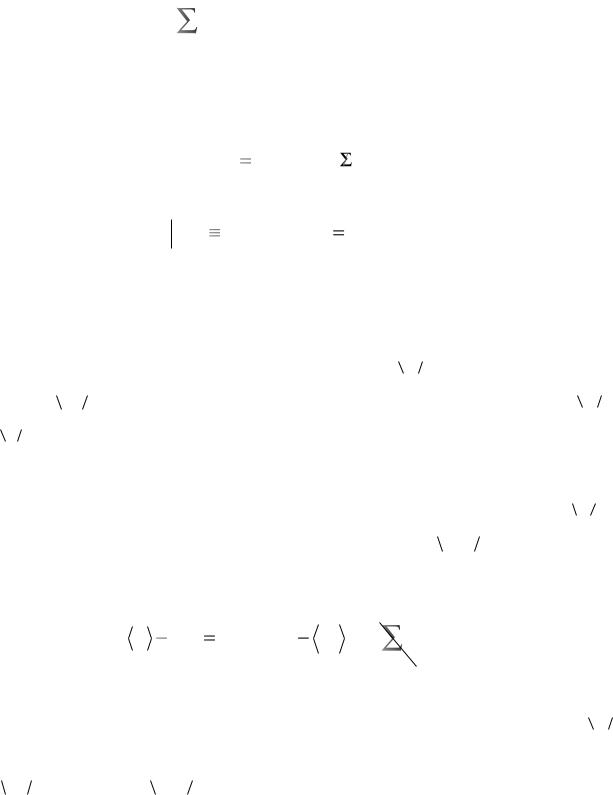
формаций, а следовательно – соответствующих напряжений), первая производная которой по пластическим деформациям определяет ρ(k ) .
В первом приближении можно принять, что упругие напряжения пропорциональны пластическим деформациям (иначе говоря, потенциал упругих напряжений представляется квадратичной функцией девиатора пластических деформаций):
ρ(k ) = |
1 N |
C e(l )p , |
C |
= C , C |
|
= const , |
(6.28) |
|
|
|
kl |
||||||
|
N l=1 |
kl |
kl |
lk |
|
|
||
|
|
|
|
|
|
|
||
Для тензора диссипативных напряжений и локальных пластических деформаций в каждой «области однородности» полагается выполняющимся соотношение теории течения (по существу, закон сухого трения при постоянном в каждой области значении сопротивления):
de(k )p |
dsk |
τ(k ) , |
, |
(6.29) |
(k ) |
τ0 k
при выполнении условия текучести:
τ(k ) |
|
τ(k ) : τ(k ) |
1/ 2 |
τ(k ) , |
(6.30) |
|
|||||
|
|
||||
|
|
|
|
0 |
|
где τ(0k ) – напряжение текучести (в данном случае – величина постоянная) k-й
области. Условие текучести и соотношения (6.29) могут быть усложнены учетом изотропного или анизотропного упрочнения.
Главной целью в настоящем подходе является получение соотношений между осредненными девиаторами напряжений  S
S и пластических дефор-
и пластических дефор-
маций 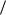 ep
ep 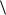 (принципиальных препятствий для введения связей между
(принципиальных препятствий для введения связей между  S
S и
и
 e
e нет, поскольку упругие деформации связываются с напряжениями про-
нет, поскольку упругие деформации связываются с напряжениями про-
стыми линейными соотношениями). Однако, к сожалению, записанных выше соотношений недостаточно. Затруднения связаны с соотношениями (6.29), не
позволяющими определить связь средних диссипативных напряжений  τ
τ со средними приращениями пластических деформаций
со средними приращениями пластических деформаций  dep
dep 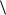 . В связи с этим
. В связи с этим
возникает потребность в дополнительных соотношениях. Е. Кренером было предложено линейное соотношение, связывающее локальные отклонения девиаторов напряжений и пластических деформаций от осредненных:
S S(k ) m |
e(k )p |
ep , |
, |
(6.31) |
(k ) |
|
|
|
|
|
|
|
k |
|
где m k – константа материала для k-й области. Полагая, что заданным явля-
ется процесс нагружения, определяемый историей изменения тензора  S
S ,
,
имеем (4N+1) тензорных (второго ранга) неизвестных S(k ) , ρ(k ) , τ(k ) ,e(k )p и 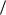 ep
ep 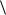 (или de(k )p и
(или de(k )p и  dep
dep 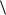 ), для определения которых имеем (4N+1) тензорных
), для определения которых имеем (4N+1) тензорных
223
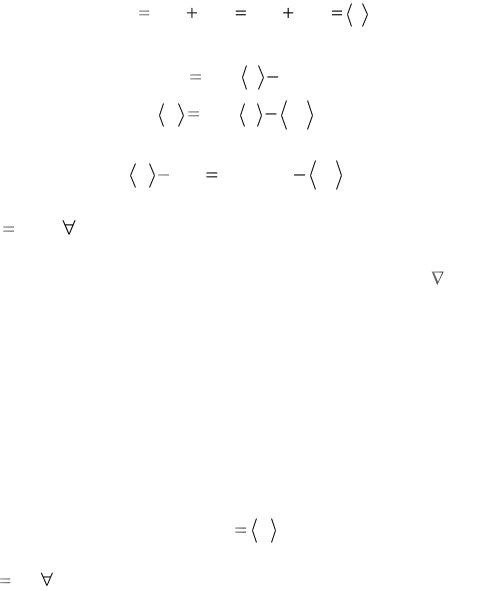
уравнений ((6.25)2 – 1 уравнение, (6.27)– N, (6.28)– N, (6.29)– N, (6.31)– N
уравнений). Таким образом, приведенная система уравнений является замкнутой.
В теориях определяющих соотношений часто используются два частных случая, применяемые при осреднении микропараметров:
а) Согласно модели Фойгта одинаковыми полагаются те или иные составляющие деформаций (или полные деформации). Для случая упругопластичности используется гипотеза об однородном распределении в предста-
вительном объеме полных деформаций
|
e(k ) e(k )e |
e(k )p |
|
S(k ) |
e(k )p e . |
(6.32) |
|
|
|
2G |
|||||
|
|
|
|
|
|
|
|
Из (6.32) |
следует: |
|
|
|
|
|
|
|
S(k ) |
2G |
e |
e(k )p |
, |
(6.33) |
|
|
S |
2G |
e |
ep . |
(6.34) |
||
Вычитая из (6.34) соотношение (6.33), получаем: |
|
||||||
|
S S(k ) |
2G e(k )p |
ep . |
(6.35) |
|||
Очевидно, что (6.35) является частным случаем (6.31) в предположении |
|||||||
m(k ) 2G |
k . Можно предложить модификацию гипотезы Фойгта (в ско- |
||||||
ростной форме), согласно которой одинаковыми по представительному объему считать градиенты вектора скорости перемещения v . При этом возможно аддитивное представление движения микрообъемов, во-первых, сум-
мой деформаций скорости D(k ) и вихря W(k ) , во-вторых, каждую из этих составляющих можно разложить на компоненты, отвечающие за упругую и не-
упругую скорости деформации D(k )e , D(k )p |
и поворот кристаллической ре- |
шетки W(k )e и «материальный» поворот |
W(k )m . |
б) Другой частный случай, известный в МСС и ТОС под названием ги-
потезы Рейсса, полагает однородным распределение напряжений (а сле-
довательно, девиаторов напряжений) в пределах представительного объема, т.е.
|
S(k ) S . |
(6.36) |
Нетрудно видеть, что соотношение (6.36) следует из (6.31) при условии |
||
m(k ) 0 |
k . |
|
Отметим, что гипотезы, приведенные выше, использовались Фойгтом и Рейссом при определении эффективных модулей упругости поликристаллов, в настоящее время они часто применяются в механике композитов. При этом ни одна из гипотез не обеспечивает точного соответствия теоретических и экспериментальных данных. Соотношения Кренера содержат набор параметров m(k ) , позволяющих за счет их выбора повысить данное соответствие.
224
Используя в приведенных соотношениях разное число элементов N, можно получить различные приближенные теории пластичности. Понятно, что увеличение числа элементов (а следовательно – числа степеней свободы модели) позволяет повышать точность определяющих соотношений. Простейший вариант теории получается при N=1 и соответствует известной модели А.Ю. Ишлинского.
Здесь остановимся на другом крайнем варианте – с бесконечно большим числом элементов. Следуя [55], вводятся обозначения: Ep , ,T – случайные тензоры девиаторов пластических деформаций, напряжений и диссипативных сил сопротивления пластическому деформированию; обозначения ep ,S, τ сохраняются для реализаций соответствующих случайных тензоров. Принимается справедливой эргодическая гипотеза, вследствие чего от осреднения по объему осуществляется переход к осреднению по множеству реализаций при сохранении обозначения 
 для осредненных величин.
для осредненных величин.
Из физического анализа процесса пластического деформирования известно, что важнейшими параметрами, определяющими движение дислокаций, реализующее пластическое формоизменение, являются характеристики различного вида препятствий (частицы включений, дислокации леса, барьеры различных типов и т.д.). «Мощность» и конфигурация этих препятствий являются стохастическими параметрами. Аналогом последних при континуальном рассмотрении можно считать диссипативные силы сопротивления пластическим деформациям, которые, в свою очередь, будут определять микродеформации и микронапряжения. В связи с вышесказанным, несколько упрощая модель, полагается, что единственным случайным параметром является интенсивность диссипативных сил Tu (реализации обозначаются че-
рез τu ). При этом полагается, что плотность распределения p τu этой слу-
чайной величины известна. В соответствии |
p τu можно поставить функцию |
|||||||||
|
|
u |
|
|
|
|
|
|
|
|
распределения ξ |
(τu ) |
p(τ'u )dτ'u . |
|
|
|
|||||
|
|
0 |
|
|
|
|
|
|
|
|
Тогда осредненные девиаторы пластических деформаций и напряжений |
||||||||||
определяются следующими соотношениями: |
|
|||||||||
|
|
|
|
|
|
|
|
1 |
|
|
ep |
|
ep (τ |
u |
)p(τ |
u |
)dτ |
u |
|
ep (ξ)dξ , |
(6.37) |
|
|
|
|
|
|
|
|
|||
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
S |
|
S(τu )p(τu )dτu |
S(ξ)dξ . |
(6.38) |
||||||
|
0 |
|
|
|
|
|
|
0 |
|
|
Гипотеза Кренера принимается практически без изменения (за исключе- |
||||||||||
нием определения осредненных величин): |
|
|
||||||||
S |
S |
m ep |
ep |
, |
m |
const . |
(6.39) |
|||
Локальный закон, соответствующий теории пластического течения, за-
225
писывается в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dep |
|
ds |
τ . |
|
(6.40) |
|||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
τu |
|
|
|
|
Аналогом соотношения (6.28) выступает следующее соотношение: |
|||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
ρ(ξ) |
C(ξ, ξ ')ep (ξ ')dξ ' . |
(6.41) |
||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
Тогда обобщение соотношения (6.27) |
представимо в виде |
||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
τ |
S C(ξ, ξ ')ep (ξ ')dξ ' , |
(6.42) |
||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
τ |
S |
|
C(τ |
u |
, τ' )ep |
(τ' )d |
τ' . |
(6.43) |
|||
|
|
|
|
|
u |
u |
u |
|
|||
|
|
0 |
|
|
|
|
|
|
|
|
|
Заметим, что в силу ограничения на константы Ckl |
в (6.28), в (6.41) – |
||||||||||
(6.43), ядро C(ξ,ξ ') |
должно |
|
быть |
симметричным. |
Вводя обозначение |
||||||
C '(ξ,ξ ') C(ξ,ξ ') |
m и подставляя (6.39) в (6.42), получаем |
||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
τ |
S |
|
mep |
|
|
C '(ξ, ξ ')ep (ξ ')dξ ' . |
(6.44) |
||||
0
Нетрудно видеть, что система соотношений (6.37), (6.40), (6.44) позволяет по заданной истории осредненных напряжений  S
S определить историю
определить историю
осредненных пластических деформаций  ep
ep  .
.
Использованный здесь подход к построению определяющих соотношений вплотную примыкает к физическим теориям и может быть использован при формулировке определяющих соотношений в различных разделах МСС.
Рассмотренный вариант квазистатистической модели относится к одноуровневым макрофеноменологическим ОС, в связи с чем в ней отсутствуют неявные внутренние переменные и эволюционные уравнения для них. Основными параметрами, существенно зависящими от микроструктуры, являются закон распределения сопротивления деформации (напряжения «сухого
трения») p τu , параметр т в модифицированной гипотезе Кренера (6.39) и ядро C(ξ,ξ ') в соотношении (6.41). Указанные параметры, как следует из фи-
зического анализа процессов пластического деформирования (см. гл. 3), зависят от величины зерен, их ориентации (взаимоориентации), типа кристаллической решетки, энергии дефекта упаковки, дислокационной субструктуры и других параметров мезо- и микроуровней.
Вопросы для самопроверки
1. Дайте определение поверхности пластичности (текучести) и пластиче-
226
ского потенциала. Как эти поверхности применяются для формулировки ОС теории пластического течения?
2.Как связаны первые инварианты тензора напряжений Коши (или средние напряжения) и тензора малых деформаций (или средние деформации) в теории пластического течения?
3.Какие способы разложения мер полных деформаций (или их скоростей) на упругую и пластическую составляющие Вам известны? В каких случаях они применимы?
4.Приведите запись модифицированного критерия текучести Мизеса. Дайте физическое толкование тензора остаточных микронапряжений.
5.Какие параметры в одноповерхностных теориях можно отнести к явным внутренним переменным и почему?
6.Запишите ОС простейшей одноповерхностной теории пластического течения, проиллюстрируйте его на примере одноосного нагружения.
7.Приведите запись уравнения для описания эволюции тензора остаточных микронапряжений в общем виде.
8.Проведите сравнительный анализ ОС вида (6.5) с соотношениями теории УПП А.А. Ильюшина (гл.5).
9.Проведите на примере одноосного нагружения качественный анализ содержащихся в табл. 6.1 модификаций одноповерхностных теорий.
10.С использованием соотношений (6.3) и (6.4) получите соотношения вида (6.5) для всех теорий, содержащихся в таблице 6.1.
11.Сформулируйте основные положения многоповерхностной теории течения З. Мруза.
12.Приведите структурно-механическую схему модели З. Мруза, проиллюстрируйте её для случая одноосного нагружения.
13.Приведите графическую иллюстрацию модели Мруза в двумерном пространстве напряжений для случая одноосного нагружения и сложного нагружения с частичной разгрузкой и последующим нагружением в направлении второй оси.
14.Повторите самостоятельно вывод соотношения (6.13) для определения движения поверхности текучести при произвольном нагружении. В каком случае из него следует закон Г. Циглера?
15.На основе какой кинематической гипотезы получено соотношение
(6.17)?
16.Приведите соотношения двухповерхностной теории течения, предложенной Я. Дафалиасом и Е. Поповым.
17.Какие модели, конкретизирующие соотношения Я.Дафалиаса и Е. Попова, Вам известны?
18.Каковы физические предпосылки для построения статистических теорий МДТТ? Каков общий «алгоритм» построения таких теорий?
19.Какие характеристики поликристаллов являются случайными? Каким образом предлагается описывать эти случайные характеристики в квазистатистической теории пластичности?
227
20.Что понимается в квазистатистической теории пластичности под «областями однородности»? Как определяются осредненные напряжения и деформации?
21.Чем обусловлено появление упругих напряжений ρ(k ) , от каких пара-
метров они зависят, как определяются в квазистатистической теории? Приведите пример, объясняющий появление упругих напряжений в случае одноосного деформирования.
22.Объясните механический смысл представления девиатора напряжений упругой и диссипативной составляющими, запишите выражение для диссипативной составляющей.
23.Запишите соотношение Кренера, объясните его на примере одноосного нагружения.
24.Осуществите проверку математической корректности квазистатистической теории пластичности (замкнутости системы уравнений).
25.Проведите сравнительный анализ гипотез Кренера, Фойгта и Рейсса, попытайтесь построить структурно-механические модели, соответствующие этим гипотезам (одномерный случай).
26.Приведите соотношения квазистатистической теории пластичности для случая бесконечного числа элементов. Проведите качественный математический анализ системы соотношений.
Любая теория пластичности представляет лишь модель явления и проверке могут подлежать только следствия из этой теории, притом с определенной степенью точности, зависящей от характера рассматриваемой задачи.
Ю.Н. Работнов
7. Эндохронная теория пластичности
Как видно из предшествующего материала (гл.2, 6), установление законов эволюции поверхности (поверхностей) нагружения представляет собой непростую задачу. В связи с этим в построении теории пластичности, начиная с работ А.А. Ильюшина, не прекращались попытки сформулировать определяющие соотношения теории пластичности, позволяющие описывать процессы произвольного нагружения, и в то же время не содержащие понятие поверхности текучести. Напомним, что достаточно общая форма ОС этого типа впервые была предложена А.А. Ильюшиным [15, 16]. Указанное ОС приведено в гл.5 (истокообразная форма ОС (5.29)).
К этому же типу теорий относится предложенная в 1971 г. К. Валанисом [88] эндохронная теория пластичности (ЭТП) (достаточно подробное из-
228
ложение теории содержится в [10, 24, 27, 53, 54]), интенсивно развивающаяся и в настоящее время. Одним из важнейших источников мотивации для автора теории была трудность определения (см. гл.2) в классической теории пластичности понятия поверхности текучести, особенно – для произвольного нагружения, в связи с чем отправным пунктом принят отказ от изначального постулирования существования такой поверхности. Следует отметить, что в более поздних работах (см., например, [90, 92]) появление такой поверхности как следствия теории автором допускается. В основу теории положено понятие так называемого внутреннего времени, что и обусловливает название теории (в последнее вошли два греческих слова: эндо – внутренний и хронос
– время). Определяющий функционал ЭТП имеет сравнительно простую структуру наследственного типа, по виду не отличающуюся от функционала линейной вязкоупругости, однако с заменой физического времени на внутреннее время.
Как и во всех предыдущих теориях, полагается, что рассматривается случай малых деформаций. В исходном варианте К. Валанисом предложена общая формулировка ОС ЭТП следующего вида [88]:
z |
dε |
|
|
σ = C(z z ) : |
dz , |
||
|
|||
0 |
dz |
||
|
|
||
где σ – тензор напряжений Коши, С – тензор свойств материала (четвертого ранга), ε – тензор малых деформаций, z – внутреннее время, определяемое
соотношениями: dη2 = dε : P : dε, dz = dη f (η) . Здесь Р – неотрицательно
определенный тензор четвертого ранга, f( ) – функция упрочнения, более подробно о ней будет сказано ниже.
В дальнейшем была принята гипотеза изотропии материала в естественной конфигурации. Принято, что первые инварианты тензоров напряжений Коши и малых деформаций связаны линейным соотношением, что позволяет перейти к анализу связи соответствующих девиаторов. Далее в настоящем разделе будет использоваться в основном векторное представление процессов нагружения (деформирования). С учетом принятых гипотез определяющие соотношения ЭТП принимают следующий вид:
|
z |
|
|
|
|
|
|
Σ |
J z |
|
z |
dэ z |
, |
(7.1) |
|
|
0 |
|
|
|
|
|
|
Внутреннее время z |
в наиболее простом случае определялось соотно- |
||||||
шением: |
|
|
|
|
|
|
|
dz |
ds |
|
, |
f s |
0 , |
(7.2) |
|
f |
s |
||||||
|
|
|
|
|
|||
В последнем соотношении ds, как и ранее, обозначает длину элементарного участка траектории (полных) деформаций, функция f(s) ответственна за эффекты изотропного упрочнения (разупрочнения) и называется обыч-
229
но функцией упрочнения; материал является упрочняющимся, если df /ds>0, и разупрочняющимся, если df /ds<0.
Для согласования со свойством затухающей памяти ядро функционала (7.1) должно быть убывающей функцией внутреннего времени z, dJ(z)/dz<0. Для конкретизации вида функции J(z) часто используются известные в теории вязкоупругости реологические соотношения. В частности, в ЭТП широко используется обобщенная модель Максвелла (структурная схема – совокупность N параллельно соединенных вязкоупругих элементов), для которой
|
N |
|
J z |
Eie iz . |
(7.3) |
|
i 1 |
|
Здесь Еi, i – материальные (положительные) постоянные, определяемые в экспериментах на сложное нагружение.
В случае N=1 для модели Максвелла (7.3) нетрудно получить дифференциальную форму записи (7.1):
dΣ 2Gdэ - αΣdz ,
т.е. ОС ЭТП представимы в «релаксационной» форме (первый член правой части играет роль «упругого предвестника», второй характеризует падение накопленных напряжений за счет неупругих процессов – «релаксацию»). Приведенная форма записи ОС ЭТП весьма наглядно демонстрирует механический смысл входящих в ОС параметров: параметр и внутреннее время совместно характеризуют «темп релаксации» напряжений. С физической точки зрения «темп релаксации» определяется микроструктурой материала, особенно – дислокационной субструктурой, наличием дефектов разной размерности и природы (см. гл. 3). Например, образование дислокационных жгутов, кос и т.д., появление дислокационных барьеров типа Ломера– Коттрелла, наличие жестких включений второй фазы должно приводить к существенному торможению процессов релаксации. С указанной точки зрения параметры и z являются (явными) внутренними переменными (см. гл.
1).
Несмотря на очевидную простоту (можно даже сказать – изящность) ОС ЭТП, они позволили качественно описать многие интересные эффекты, наблюдаемые при пластическом деформировании. В частности, ЭТП качественно достаточно хорошо описывает эффекты линейного и нелинейного упрочнения, гистерезис и стабилизацию петель гистерезиса при циклическом деформировании, «нырок» в интенсивности напряжений в окрестности точки излома траектории деформации и ряд других [53]. В то же время количественное соответствие экспериментальных данных и результатов расчетов с помощью ЭТП (в рассматриваемом начальном варианте) нельзя признать удовлетворительным.
Причиной указанного несоответствия является, как отмечается в [53], отсутствие в ОС (7.1)–(7.3) зависимости от сложности нагружения, «переупрощенность» уравнений по сравнению с общим видом ОС пластичности или с достаточно общей истокообразной формой (5.29) определяющих соотно-
230
