Теория определяющих соотношений. Часть 2. Теория пластичности

Ковалентная (или гомеополярная) осуществляется за счет «обобществления» соседними атомами двух или более электронов внешней оболочки, которая таким образом оказывается заполненной до восьми электронов; связь характерна для атомов, имеющих внешнюю оболочку, заполненную не менее чем наполовину.

Молекулярная связь реализуется за счет сил Ван-дер-Ваальса, обусловленных эффектом поляризации соседних атомов; поляризация происходит при случайных флуктуациях орбит электронов одного из атомов, что ведет к поляризации соседних атомов и появлению дипольных моментов.

Металлическая связь осуществляется за счет «обобществления» большими группами атомов слабо связанных с атомами валентных электронов; электроны, оторвавшиеся от своих атомов, равномерно распределены по объему кристалла (образуют так называемый электронный газ) и движутся по сложным траекториям таким образом, что в каждый момент времени уравновешивают силы отталкивания положительных ионов. Металлическая связь представляет собой более общий случай ковалентной.

Различные виды связей не исключают друг друга, они могут действовать одновременно (смешанная связь) или заменять одна другую при изменении состояния кристалла (например, при изменении температуры).

Для описания движения атомов в молекулярной динамике широко используются так называемые потенциалы межатомных взаимодействий, характеризующие потенциальную энергию взаимодействия атомов. Независимо от конкретного вида связей потенциальная энергия П(ij) атомов i,j с достаточной для решения многих задач точностью описывается соотношением, общий вид которого был предложен А.Ф.Иоффе:

где А, В, m, n – (положительные) константы материала, m, n – как правило, целые числа, причем n > m, rij = |ri – rj| – расстояние между атомами i,j. При этом не учитываются эффекты «экранирования» взаимодействия атомов. Полагая взаимодействие потенциальным, силы взаимодействия атомов определяются дифференцированием потенциальной энергии по rij . Качественно характер изменения потенциальной энергии и силы взаимодействия F(ij) двух атомов от расстояния между ними изображен на рис. 3.1. Нулевое значение силы взаимодействия, отвечающее минимуму потенциальной энергии взаимодействия, определяет равновесное расстояние между атомами.

Потенциальная энергия произвольной совокупности атомов определяется как сумма потенциальных энергий всех пар атомов. Отметим, что для ионной и ковалентной связей потенциальная энергия взаимодействия составляет порядка 10 эВ/ атом, для молекулярных (самых «слабых») связей – порядка 0.1 эВ/ атом, металлические связи имеют промежуточные значения энергии взаимодействия.

110

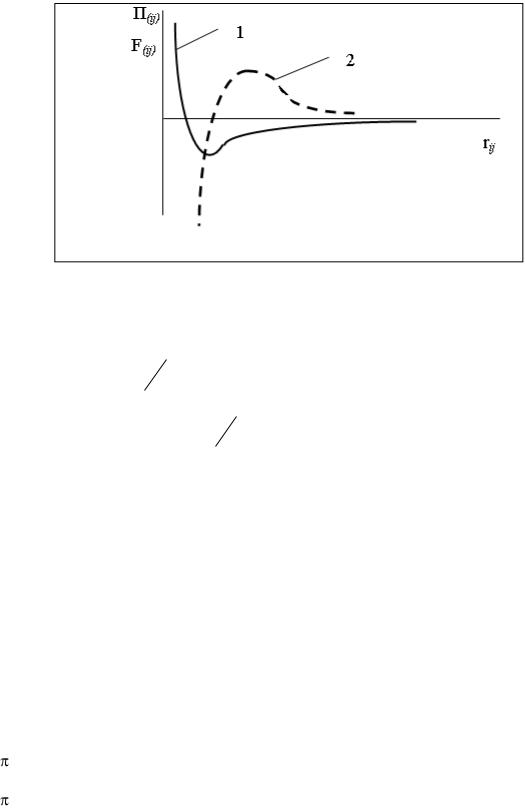
Рис. 3.1. Зависимость потенциальной энергии (1) и силы взаимодействия (2) двух атомов от расстояния между ними

При температуре, отличной от нулевой (по шкале Кельвина), кроме потенциальной атомы обладают кинетической энергией колебательных движений, средняя величина кото-

рой определяется как T = 3 2 k θ , где k – константа Больцмана, θ – абсолютная темпера-

тура; при этом считается, что на каждую из трех степеней свободы в колебательном дви-

жении приходятся равные доли, т.е. 12 k θ . При комнатной температуре кинетическая

энергия равна примерно 0.03 эВ. Заметим, что в кристаллах всегда имеют место флуктуации (отклонения от среднего значения) кинетической энергии, в силу чего, несмотря на весьма малую величину кинетической энергии по сравнению с характерной энергией образования точечных дефектов, вероятность их образования отлична от нулевой, причем вероятность растет по экспоненциальному закону с ростом температуры.

Типы кристаллических решеток

Для макросвойств металлов и сплавов, которые в подавляющем большинстве имеют кристаллическое строение, весьма важными являются тип и параметры кристаллической решетки исследуемого материала. В частности, указанные характеристики определяют анизотропию упругих и пластических свойств кристаллитов (зерен, субзерен), а в силу этого – и особенности деформирования поликристаллов. В связи с этим остановимся на некоторых понятиях кристаллографии [66].

Элементы симметрии (плоскости, оси, центры) встречаются в кристаллах в различных сочетаниях. Пусть решетка переходит сама в себя при повороте вокруг некоторой оси на угол 2 /n (n = 1,2,...), тогда данная ось называется осью симметрии или поворотной осью n-го порядка и обозначается как Сn. Если решетка переходит сама в себя при повороте на угол 2 /n (n=1,2,...) вокруг некоторой оси и одновременном отражении относительно плоскости, перпендикулярной к этой оси, то последнюю называют зеркальноповоротной осью n-го порядка и обозначают как Sn. В ФТТ показано, что поворотные и зеркально-поворотные оси (симметрии) кристалла могут быть только осями 2-го, 3-го, 4- го и 6-го порядков. Существуют оси симметрии, которые являются единственными, не повторяющимися с помощью операций симметрии, присущих данному кристаллу (например, отражения оси симметрии относительно плоскости симметрии). Такие направления называются особыми или единичными. К ним относится, например, ось шестого порядка в

111

шестигранной призме. В то же время в кубе вообще отсутствуют единичные направления, для любой оси симметрии можно найти эквивалентные ей направления.

По свойствам симметрии и числу единичных направлений кристаллы подразделяются на

три категории: высшую, среднюю и низшую.

Квысшей категории относятся кристаллы, не имеющие особых направлений, имеющие несколько осей симметрии порядка выше второго. Анизотропия в таких кристаллах выражена слабее всего. Внешняя форма кристаллов высшей категории симметрии является «изометричной», т. е. развита примерно одинаково по всем направлениям (куб, октаэдр). Кристаллы средней категории имеют одно особое направление – одну ось симметрии порядка выше второго. Анизотропия физических свойств более ярко выражена, особенно в направлениях вдоль особой (главной) оси симметрии и перпендикулярно ей. Характерные формы кристаллов данной категории – призмы, пирамиды.

Книзшей категории относятся кристаллы, не имеющие осей симметрии порядка выше второго и (или) обладающие несколькими особыми направлениями. Эти кристаллы имеют наиболее ярко выраженную анизотропию свойств.

Три категории кристаллов подразделяются на семь кристаллических систем или сингоний (сингония (греч.) – сходноугольность). В сингонию объединяются типы кристаллов, имеющих одинаковую симметрию элементарных ячеек и одинаковый тип (кристаллографической) системы координат. В общем случае последние представляют собой косоугольные системы координат с различными масштабными отрезками вдоль разных осей. Отметим, что в кристаллографии используется только правая система координат. Выбор системы координат согласуется с симметрией рассматриваемого кристалла. Оси координат выбираются по осям симметрии или по нормалям к плоскостям симметрии, а при недостаточности этих элементов — по ребрам кристаллического многогранника (как в кристаллах низшей категории симметрии).

Квысшей категории относится одна сингония – кубическая. Кристаллографическая система координат здесь – декартова ортогональная.

Средняя категория содержит три сингонии – тригональную, тетрагональную и гекса-

гональную. Кристаллографические системы координат в этом случае – косоугольные или

ортогональная (для тетрагональной решетки) декартовы, в качестве одной из осей обычно принимается главная ось симметрии (особое направление). Ось Ox3 перпендикулярна плоскости Ox1x2, масштабные отрезки по осям Ox1 и Ox2 одинаковы, так что анизотропия

кристаллов характеризуется обычно геометрическим параметром, равным отношению масштабов вдоль осей Ox3 и Ox1 (или Ox2).

Книзшей категории относятся три сингонии — ромбическая, моноклинная и трик-

линная. Система координат здесь или декартова ортогональная (для ромбической), или косоугольная декартова (для моноклинной (с осью Ox3, перпендикулярной плоскости симметрии Ox1x2) и триклинной) с различными масштабами вдоль всех трех осей. Остановимся подробнее на семи известных кристаллических системах (сингониях) и четырнадцати типах элементарных ячеек.

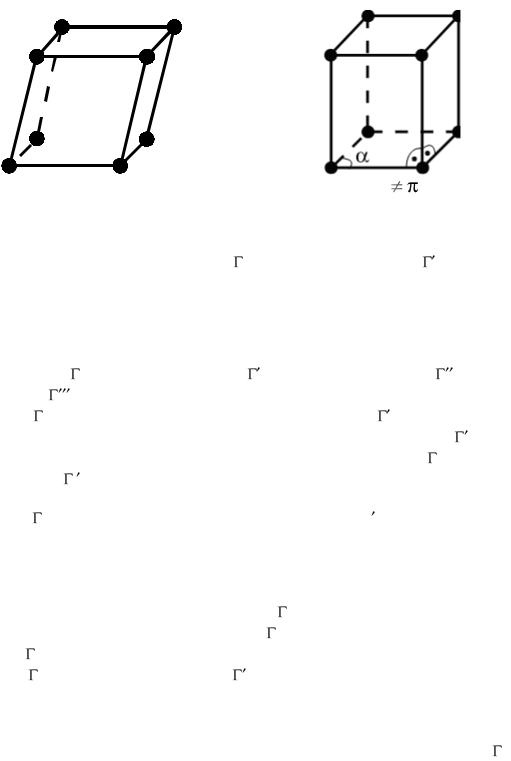
1. Триклинная система. Элементарная ячейка (рис. 3.2) в этом случае представляет собой произвольный параллелепипед (с ребрами различной длины и произвольными углами). Допустимые трансляции имеют различные длины и углы между векторами трансляции. Триклинная система не обладает поворотными осями (симметрии).

112

2. Моноклинная система. Элементарная ячейка (рис. 3.3) представляет собой прямоугольную призму, в основании которой лежит параллелограмм общего вида. Существуют два типа решетки данной системы — простая ( m) и базоцентрированная ( m), образуемая из простой добавлением узлов в центры одной из пар прямоугольных граней. Голоэдрия моноклинной системы характеризуется наличием одной поворотной оси (симметрии)

второго порядка (C2).

3. Орторомбическая (ромбическая) система. Элементарной ячейкой является прямо-

угольный параллелепипед с неравными ребрами. Существуют четыре типа решеток дан-

Простая решетка v имеет один атом. Базоцентрированная решетка v образуется из простой добавлением в центры одной из пар параллельных граней узлов; решетка v содержит два узла и может быть образована наложением двух простых решеток v. Гранецентрированная решетка v образуется из простой добавлением узлов в центры всех шести граней; решетка содержит 4 узла и может быть образована совокупностью четырех вложенных решеток v. Наконец, объемноцентрированная решетка 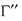v образуется из простой добавлением узла в центр параллелепипеда, содержит два узла и образуется двумя простыми решетками.

Голоэдрия орторомбической системы характеризуется наличием трех неэквивалентных поворотных осей второго порядка.

Голоэдрия тетрагональной системы характеризуется одной осью симметрии 4-го поряд-

ка и двумя неэквивалентными осями 2-го порядка (одна из них параллельна ребру, а

вторая — диагонали квадрата, лежащего в основании).

5. Тригональная система. Решетка тригональной (или ромбоэдрической) системы rh образуется из равноотстоящих плоских решеток, каждая из которых состоит из равносторонних треугольников, сдвинутых относительно друг друга (рис. 3.4). Сдвиг осуществляется таким образом, что узлы второго слоя находятся над центрами треугольников первого слоя, а узлы третьего слоя — над центрами треугольников второго слоя. Далее выполняются условия периодичности (узлы n-го слоя расположены перпендикулярно базовой плоскости над узлами (n-3)-го слоя на расстоянии 3a от (n-3)-го слоя; a — расстояние между слоями).

Голоэдрия данной системы характеризуется осью симметрии 3-го порядка, перпендикулярной базовой плоскости и лежащей в последней осью симметрии 2-го порядка.

113

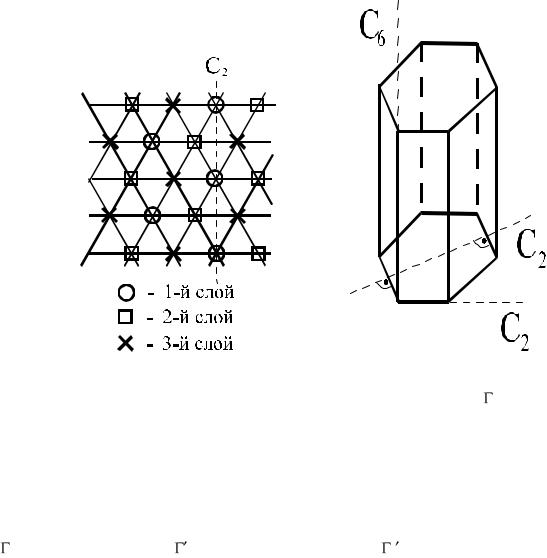
Рис. 3.4. Тригональная система Рис. 3.5. Гексагональная система

6. Гексагональная система. Решетка гексагональной системы h, как и в предыдущем случае, может быть получена путем сдвигов плоских решеток перпендикулярно базовой плоскости. Ячейка (рис.3.5) представляет собой прямоугольную призму с правильным шестиугольником в основании.

Голоэдрия гексагональной решетки характеризуется осью симметрии 6-го порядка и двумя неэквивалентными осями симметрии 2-го порядка, параллельными плоскости основания.

7. Кубическая система. Имеются три разновидности решеток данной системы: простая

c, гранецентрированная c и объемноцентрированная c. Простая решетка представляет собой куб с узлами в вершинах. Кубическую систему можно рассматривать как частный случай двух предшествующих систем (орторомбической и тетрагональной).

Голоэдрия кубической системы характеризуется осью 2-го порядка (диагональ грани), осью 3-го порядка (пространственная диагональ куба) и осью 4-го порядка (ребро куба).

Кристаллографические направления и плоскости

Как известно, кристаллические тела существенно анизотропны по теплофизическим и физико-механическим характеристикам, в связи с чем целесообразно введение некоторой «внутренней» системы координат для выделения направлений и плоскостей кристалла. Такую систему, связанную с расположением атомов в кристалле, называют кристаллографической системой координат (КСК). Заметим, что КСК широко используется при анализе напряженно-деформированного состояния монокристаллических деталей (например, монокристаллические литые лопатки газотурбинных двигателей) и при построении соотношений физической теории пластичности.

Рассмотрим простую кристаллическую решетку с расположенными в узлах атомами (ионами); один из узлов выберем в качестве начала координат O и соединим его векторами t1, t2, t3 с ближайшими узлами, не лежащими одновременно в одной плоскости (рис. 3.6).

114

Введенная таким образом система координат Ox1x2x3 с базисными векторами t1, t2, t3 (в общем случае не ортогональными и ненормированными) и является кристаллографической

системой координат. Тогда любое направление l0 = l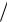l полностью определяется компонентами вектора l0 или l в базисе ti:

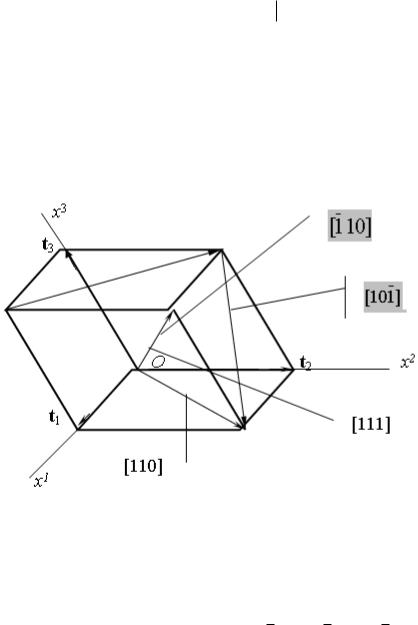
В кристаллографии, ФТТ и материаловедении обычно используются только такие векторы направлений l, компоненты которых в базисе ti суть целые числа, определяемые делением значений компонент на модуль наибольшего общего делителя. Совокупность определенных таким образом компонент называются индексами Миллера и записываются как [l1 l2 l3]. В случае отрицательных значений компонент знак «минус» ставится над индексом. Для примера на рис 3.6 показаны несколько направлений и соответствующих индексов Миллера; оси Ox1, Ox2, Ox3 имеют индексы Миллера [100], [010], [001] соответственно.

Рис. 3.6. Примеры индексов Миллера кристаллографических направлений

Совокупность кристаллографических направлений, получающихся из заданного [l1 l2 l3] ортогональными преобразованиями симметрии рассматриваемой кристаллической решетки, называются системой кристаллографических направлений и обозначаются как

< l1 l2 l3 > . Например, для кубической решетки система кристаллографических направле-

ний <100> включает направления [100], [010], [001], [100], [010], [001].

Наряду с направлениями в ФТТ и материаловедении широко используются обозначения атомных плоскостей (т.е. плоскостей, проходящих через совокупность атомов в узлах решетки), для определения которых вводят так называемые кристаллографические обозначения (также называемые индексами Миллера). Индексы Миллера некоторой произвольной плоскости определяются следующим образом: находятся точки пересечения плоскости с осями кристаллографической системы координат, т.е. устанавливаются координаты этих точек в долях размеров ячейки по соответствующим направлениям, вычисляются обратные к ним величины и делятся на наибольший общий делитель (точнее – его модуль), т.е. приводятся к целочисленным значениям (как и в индексах направлений, знак «минус» ставится над соответствующим индексом). Полученная тройка чисел и представляет собой индексы Миллера плоскости. Примеры обозначения некоторых плоскостей приведены на рис. 3.7.

115

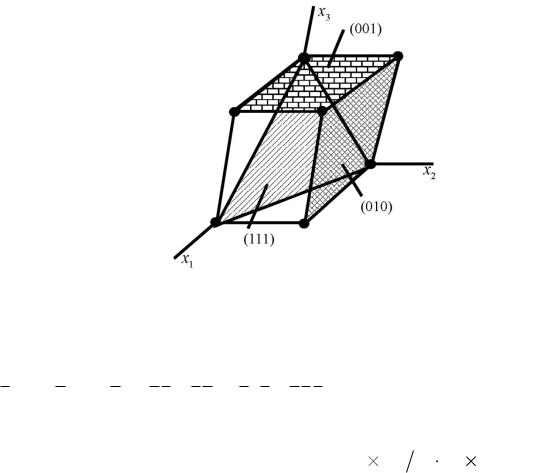
Рис. 3.7. Примеры индексов Миллера кристаллографических плоскостей

Конкретная плоскость обозначается как (A1A2A3); совокупность плоскостей, получаемых из некоторой заданной преобразованиями симметрии рассматриваемого типа кристалла, называется системой плоскостей и обозначается как {A1A2A3}. Например, для кубической решетки система плоскостей {111} включает плоскости (111),

(111),(1 11),(11 1),(1 1 1),(1 11),(11 1),(1 1 1) .

Заметим, что определение индексов Миллера плоскостей может быть осуществлено с использованием векторного произведения двух векторов, лежащих в данной плоскости; ком-

по модулю 3), приведенные к целочисленным значениям, совпадают с индексами Миллера плоскости.

Введенная система индексов для кристаллографических направлений и плоскостей применима для любых кристаллов, однако для гексагональной решетки возникают определенные сложности определения индексов Миллера. В связи с этим для гексагональных решеток применяются так называемые индексы Браве, представляющие совокупность четырех целых чисел (знак «минус», как и ранее, ставится над индексом). Для этого в базисной плоскости вводятся три оси с векторами «базиса» t1, t2, t3= –t1–t2, четвертая ось совпадает с главной осью симметрии, ее базисный вектор обозначим как t4 (рис. 3.8).

116

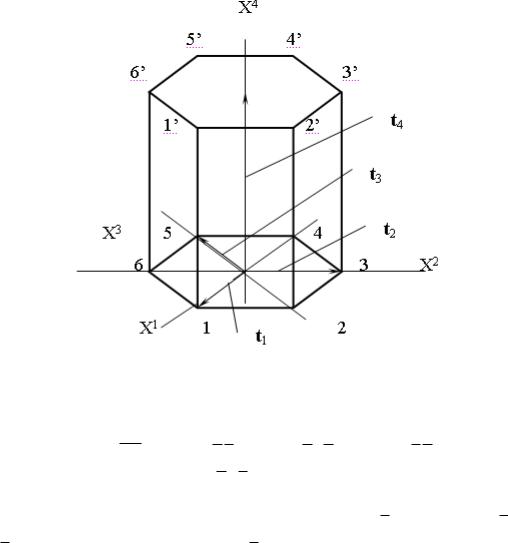
Рис. 3.8. Гексагональная решетка

Нетрудно видеть, что компоненты любого вектора r в разложении по этим четырем «базисным» векторам ti должны удовлетворять следующему свойству: r3= –r1 – r2; иначе говоря, сумма первых трех индексов Браве всегда равна нулю. В качестве примера укажем ин-

дексы Браве осей Oxi, i = 1, 4 : Ox1 – [2 1 10], Ox2 –[12 10] , Ox3 – [1 120] , Ox4 – [0001];

направление 12’ имеет индексы Браве [12 11] .

Индексы Браве кристаллографических плоскостей определяются аналогично индексам Миллера; например, плоскость 122’1’ имеет индексы Браве (10 10) , 233’2’ – (01 10) ,

344’3’– (1100) , 123456 – (0001), 133’1’– (1120) . Указанное выше свойство индексов Бра-

ве сохраняется и для индексов плоскостей, т.е. сумма первых трех индексов равна нулю, что является прямым следствием равенства индексов плоскостей индексам направлений нормалей к этим плоскостям.

117

Стереографические проекции

Как отмечалось, кристаллические материалы являются существенно анизотропными по широкому спектру свойств, в частности – по упругим и пластическим свойствам (более детально последние будут рассмотрены в главе, посвященной физической теории пластичности). На макроуровне поликристаллы в силу хаотической ориентации кристаллитов (зерен) обычно полагаются изотропными; однако глубокие пластические деформации могут порождать образование текстуры – появление некоторых предпочтительных для того или иного процесса обработки ориентаций кристаллитов. При анализе кристаллографии неупругих деформаций, в особенности при рассмотрении фрагментации и текстурообразования, широко используются так называемые стереографические проекции, с помощью которых достаточно наглядно определяются кристаллографические направления, плоскости и углы. Во многих случаях для качественного решения вопроса о приемлемости гипотезы изотропии или того или иного типа анизотропии бывает достаточно одного взгляда на стереографическую проекцию исследуемого поликристаллического материала.

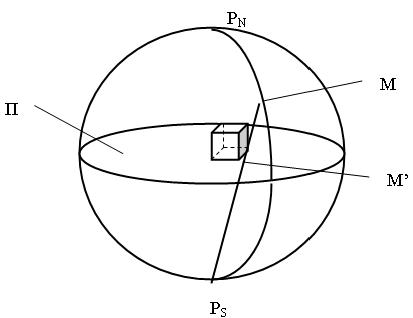
Рассмотрим стереографические проекции на примере наиболее распространенных кристаллов кубической системы. Расположим элементарную ячейку в центре сферы (рис. 3.9), проведем экваториальную плоскость, разделяющую сферу на две полусферы – «северную» и «южную», максимально удаленные от экваториальной плоскости точки назовем полюсами (соответственно «северным» и «южным»). Выбирая любое направление (или плоскость, определяя ее нормалью) и продолжая его до пересечения со сферой, находим так называемую сферическую проекцию направления (плоскости). Для установления стереографической проекции соединяем прямой линией точку сферической проекции с полюсом противоположной полусферы; точка пересечения этой прямой с «экваториальной» плоскостью и определяет стереографическую проекцию направления (плоскости). На рис. 3.9 показан пример определения проекций для направления r: M – сферическая, M’ – стереографическая проекция, П – экваториальная плоскость, PN и PS – «северный» и «южный» полюса.

Рис. 3.9. Сферические и стереографические проекции

На рис 3.10 приведены стереографические проекции основных направлений (плоскостей) кристалла кубической системы.

118

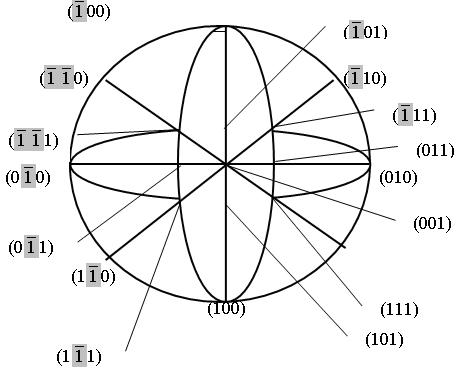
Рис. 3.10. Стереографические проекции основных направлений (плоскостей) кристалла кубической системы

Следует отметить, что для кристаллов обычно нет необходимости рассматривать всю стереографическую проекцию, в силу свойств симметрии достаточно рассмотреть лишь ее часть. Так, для кристаллов высшего класса симметрии – кубического – из изображенных на рис. 3.10 двадцати четырех стереографических треугольников достаточно рассмотреть лишь один, например, {(001), (011), (111)}. Необходимо заметить, что индексы любой плоскости могут быть определены как сумма индексов двух плоскостей, лежащих по обе стороны от рассматриваемой, сферические проекции которых расположены на одной дуге большого круга, что можно использовать для проверки правильности определения стереографических проекций.

Стереографические проекции широко используются в теории пластичности для анализа «разворотов» кристаллической решетки моно- и поликристаллов в процессе деформирования. Одним из классических примеров является исследование поворотов кристаллической решетки монокристалла при одноосном растяжении (сжатии) вдоль фиксированного в пространстве направления; в этом случае используется «обращенное движение», т.е. показывается не изменение направления кристаллографических направлений и плоскостей, а изменение кристаллографической проекции направления растягивающей (сжимающей) силы. При исследовании текстур, возникающих при различных процессах пластической обработки (деформирования) материалов, стереографические проекции используются при построении так называемых полюсных фигур (графического изображения функций распределения Pnkl, представляющих собой вероятность совпадения нормали к выделенной кристаллографической плоскости с различными направлениями в образце (или характерными направлениями исследуемого процесса)).

Полиморфные модификации

Предметом теории пластичности является изучение поведения только твердых тел, поэтому здесь не рассматриваются расплавы и процессы кристаллизации. В то же время при изучении поведения конкретных материалов следует помнить, что их свойства весьма су-

119