Теория определяющих соотношений. Часть 2. Теория пластичности

но (9.17) напряжения сдвига (а следовательно , и тензор напряжений) изменяются в k1 / n раз. Следует подчеркнуть, что из опред е- ления тензора свойств P очевидна нелинейность соотношения

(9.18), поскольку τ(k) определяется по искомому тензору S. Принимается закон изотропного упрочнения . Эволюционное

уравнение для критического напряжения имеет вид закона Воуса

(Voce):

пряжение насыщения. Макроскопический девиатор напряжений определяется осреднением с весами по всем зернам.

Отмечается, что степенной закон (9.17) может рассматриваться лишь как приближенный закон, не имеющий под собой должного физического обоснования. В связи с этим в работе пре д- лагается модифицировать указанный закон для учета скорости деформации в широком диапазоне ее варьирования и влияния те м- пературы. В основу указанной модификаци и положена так называемая модель механического порогового напряжения ( MTS-модель

(the mechanical threshold stress model)), предложенная Фоллансби и Куксом [Д14] . Последняя представляет собой изотропную «ск а- лярную» модель для предсказания напряжения течения в зависим о- сти от скорости деформации, температуры и текущего состо я- ния, описываемого параметром состояния, называемым механич е- ским порогом. При использовании этой модели для поликристаллов эффективное одноосное напряжение заменяется на критическое напряжение сдвига τ(k)c , а эффективная одноосная скорость дефо р-

мации – на суммарную скорость сдвигов по всем системам скол ь- жения. При этом рассматривается только изотропный закон у п- рочнения Тейлора, поскольку учет скоростной чувствительности и упрочнения по каждой системе скольжения весьма сложны.

Для устранения скоростной чувствительности из соотнош е- ния (9.17) (при фиксированном n, обычно принимаемом равным 20) γ0 в нем заменяется на интенсивности скорости деформации De =

(2/3 D:D)1 / 2 , что согласуется с принятой в модели Тейлора гип о- тезой Фойгта. Действительно, в этом случае при изменении D в k раз аналогичным образом в соответствии с (9.14)1 меняются ско-

291

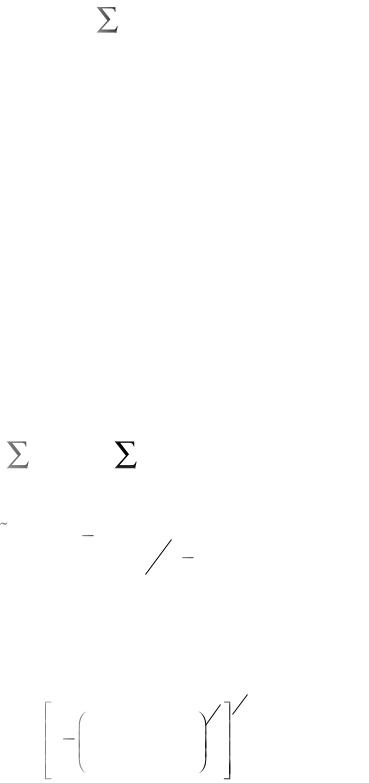
рости сдвигов, тогда согласно (9.17) напряжения сдвига остаются неизменными.

Критическое напряжение сдвига τ(k)c для учета влияния скоро-

сти деформации и температуры масштабируется «механическим порогом» τˆ , представляющим собой сопротивление сдвигу при 0 К: последний разделен на атермическую составляющу ю τˆa и термиче-

скую составляющую τˆlt , так что

l

Следует отметить, что использование термина «термическая составляющая» (введенного в

исходной статье [Д14]) для второго члена правой части (9.21) представляется не совсем

корректным, поскольку «пороговое напряжение» τˆ определено как сопротивление сдвигу при нулевой абсолютной температуре, а первый член правой части по определению не за-

висит от температуры θ .

Отмечается, что составляющая τˆa характеризует нечувствительное к скорости взаимодействие дислокаций с дальнодейс т- вующими барьерами (например, границами зерен), а τˆlt – чувстви-

тельные к скорости деформации взаимодействия дислокаций с близкодействующими препятствиями (например, дислокациями л е- са, примесными атомами), которые могут быть преодолены за счет термической активации. При изменяющихся температурах и скоростях деформации соотв етствующий вклад в критическое н а- пряжение сдвига τlt связан со своим исходным аналогом τˆlt мас-

штабирующей функцией Slt (De , θ) , так что τlt = τˆlt Slt (De , θ) .

Критическое напряжение сдвига для всех СС определяется аналогично «механическому порогу»:

Здесь G0 – некоторое отсчетное значение модуля сдвига G, определяемого соотношением:

D0, θ 0 – экспериментально определяемые константы.

Для описания кинетики взаимодействия на короткодейству ю- щих препятствиях используется соотношение Аррениуса и феном е- нологическое выражение для свободной энергии как функции н а-

292

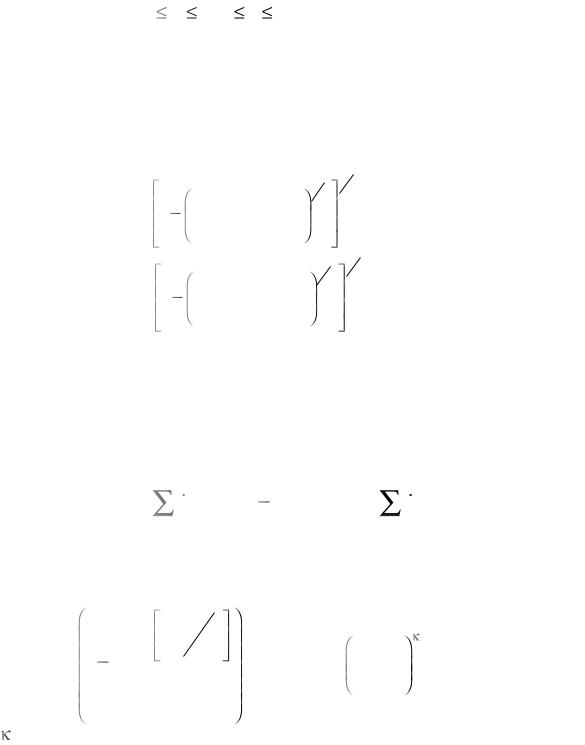
Здесь k – константа Больцмана, b – модуль вектора Бюргерса, g0 – нормализованная энергия активации дислокаций для преодоления препятствий, De 0 константа, p,q – константы, характеризующие

В этих соотношениях τˆi описывает термическую составля ю-

щую сопротивления деформации (в данной работе этот член не учитывается), а τˆε – взаимодействие подвижных дислокаций с л е-

где h0 отражает упрочнение, обусловленное накоплением дислокаций (принимается постоянным), а hr описывает скорость динамического возврата. Наиболее употребимыми функциональными формами скорости упрочнения h являются запись через гиперболический тангенс (Фоллансби–Кукс), или в виде степенного закона (Кукс и др.):

отношениях h0 описывает начальную скорость упрочнения; скорость упрочнения h с ростом деформации уменьшается и стремится к насыщению. Применение подобных моделей для деформаций, превосходящих единицу, исключено, так что невозможно описать IV стадию упрочнения.

Пороговое напряжение насыщения τˆεs является функцией скорости деформации и температуры:

293

где De0ε , g0εs , τˆεs0 – эмпирические константы.

Рассматриваемая MTS-модель является, таким образом, н е- значительной модификацией вышеизложенной модели поликр и- сталла. Уравнения (9.17), (9.19) и (9.20) теперь запишутся в виде

где использована степенная зависимость (9.28)2.

Подробно описывается численная процедура; для интегрирования по времени используется неявная разностная схема, система нелинейных уравнений решается методом Нью- тона–Рафсона (Ньютона–Канторовича). Для установления шага по времени решена задача на одноосное сжатие при 10, 20, 40 и 100 постоянных шагах по времени; различие между результатами расчета напряжения сжатия при 10 и 100 шагах не превысило

0.24%.

Верификация предлагаемой модели осуществляется сопоста в- лением полученных с ее помощью результатов ра счета напряжений с результатами стандартной изотропной модели MTS. Скоростная и температурная зависимости определялись в опытах на сжатие алюминиевого сплава Al 5182 при температурах 200 и

300о С при скоростях деформации 0.001 и 1.0 с – 1 . Показано очень хорошее соответствие результатов.

Анализ предсказания моделью формирования текстуры осущ е- ствлен сопоставлением с результатами, полученными Kalidindi

e.a. с использованием модели Тейлора; отмечается хорошее кач е- ственное соответствие результатов.

Отдельный раздел работы посвящен процедуре идентификации модели. С этой целью записывается функция квадратичного о т- клонения определяемых расчетным путем компонент тензора н а- пряжений от экспериментально измеряемых значений . Для регуляризации добавлен штрафной член, представляющий собой квадратичное отклонение искомых параметров модели от первоначально заданных. Решение поставленной задачи минимизации этой фун к- ции осуществлялось градиентным методом. Проведены расчеты для случаев сжатия и кручения образцов из стали HY100 (ОЦК– решетка, в рассмотрение включены все 48 потенциально возмо ж- ных систем скольжения) при различных скоростях деформации и

294

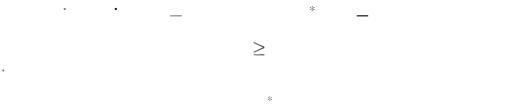
температурах. Полученные результаты позволили с удовлетвор и- тельной точностью описать поведение стали при отсутствии н а- чальной текстуры. Аналогичные результаты получены для начал ь- но текстурированной танталовой пластины.

Представляется целесообразным кратко остановиться на р а- боте [Д5], содержащей значительное количество экспериментал ь- ных данных по лучевым и двухзвенным траекториям деформации листового алюминиевого сплава, пригодным для идентификации и верификации теоретических моделей. Подробно описана методика экспериментальных исследований, включающих как чисто механ и- ческие измерения, так и анализ текстуры и дислокационных су б- структур. Теоретические исследования проведены с использован и- ем вязкопластических моделей со степенным законом, «полностью стесненной» и самосогласованной. Обе модели дают близкие р е- зультаты как по зависимостям напряжений от работы на пластич е- ских деформаций, так и по полюсным фигурам . Отмечается, что полюсные фигуры в теоретических расчетах получаются более четко выраженными, чем в экспериментах.

Г. Упруговязкопластические модели

Одной из первой работ, в кот орой представлены теоретические результаты, удовлетворительно согласующиеся с экспер и- ментальными данными, была статья [Д36] . Модель, предложе н- ная в цитируемой работе, базируется на теории термоактив и- руемого движения дислокаций ( Kroner&Teodosiu (1972), Kratochvil&de Angelis (1971)) и модели Линя.

В предлагаемой модели приняты все гипотезы модели Линя, за исключением соотношений для определения скоростей (или прир а- щений) сдвигов: предполагается, что скорости сдвигов связаны с касательными напряжениями на кристаллографических системах скольжения вязкопластическими соотношениями вида

где γ0 – константа материала, Н0 – величина энергетического барьера (Пайерлса); k – кон-

станта Больцмана; θ – температура (К); ν – константы, относящиеся к объему препятствий (активационный объем); τ(k ) , τ(ck ) – касательное напряжение и критическое напряже-

τ(k )

ние сдвига в k-й системе скольжения, причем c характеризует сопротивление сдвигу

препятствий, не преодолеваемых за счет термической активации и связанное с дальнодействующими полями напряжений; К – число систем скольжения (для рассматриваемых в работе ГЦК-кристаллов принято К = 24, т.е. удвоенное число кристаллографических сис-

295

K

τ(ck ) = A γ(i) [B(τ(ck ) τˆc )]m exp[ QD/(kθ)] , k =1, K , (9.33)

i =1

где А, В, m, τˆc – материальные константы, QD – энергия активации диффузии.

В качестве основы конститутивной модели, как и в модели Линя, используется (изотропный) закон Гука, записанный в скор о- стях. Численная процедура реализуется пошагово, задается ист о- рия осредненных скоростей полных деформаций (используется г и- потеза Фойгта).

Предлагаемая модель была апробирована для случая простого и сложного (на двухзвенных траекториях с изломами на углы 30, 60, 90, 120, 150 и 180о ) нагружения поликристаллического алюм и- ния при изотермическом деформировании при температуре 200 о С и скоростях деформирования от 3х10 - 5 до 3х10- 3 . Результаты расчетов находятся в удовлетворительном соответствии с экспериме н- тальными данными; в частности, хорошо описывается эффект «нырка» (резкого падения интенсивности напряжений в окрестн о- сти точки излома траектории деформации).

К рассмотренной выше работе вплотную примыкает стат ья [Д37], в которой более детально рассматривается процедура орие н- тационного осреднения тензора напряжений. Рассмотрена также модификация модели для реализации процесса нагружения в пр о- странстве напряжений. Отмечается возможность использования вместо гипотезы Фойгта самосогласованной модели Кренера.

Обзор работ по физическим теориям пластичности, вязко - и упруговязкопластичности, выполненных до 1985 года, содержится в статье [Д2]. Предлагаемая в работе модель ориентирована на описание образования текстуры при больших пластических дефо р- мациях и с этой точки зрения представляется целесообразным её достаточно полное изложение.

В качестве исходного кинематического соотношения также используется вариант мультипликативного разложения

где тензор F* описывает как упругое деформирование, так и кв а- зижесткие повороты, тогда как Fр полностью определяется сдвигами по кристаллографическим системам скольжения (СС).

Рассмотрим разложение (9.34) в терминах конфигураций и базисных векторов. Наряду с отс четной К0 и актуальной Кt конфигурациями в разложении участвует промежуточная конфигурация К*, получаемая из К 0 преобразованием Fр . Векторы основного (сопряженного) базисов в этих конфигурациях обозначим соответственно

o o

как ei ei , eˆi eˆi , ei ei . В терминах базисных векторов входящие в

296

разложение (9.34) тензоры можно представить следующим образом

[57]:

ми и ортогональными, т.е. влиянием упругих искажений решетки пренебрегается. Тогда пластическая составляющая градиента

скорости перемещений ˆ vT = F F-1 выражается через скорости сдвигов следующим образом:

моделях физической теории пластичности принято использовать её симметричную часть M((S)k ) , вводя разложение

где M((A)k ) – антисимметричная составляющая диады. С использов а-

нием разложения (9.38) входящие в (9.37) пластические составляющие девиатора деформации скорости и спина можно записать в виде

С использованием (9.34)–(9.35) можно получить следующие соотношения:

297

Из (9.41)2 следует, что «пластическая составляющая» в разлож е- нии (9.40) представляет собой скорость изменения компонент метрического тензора в конфигурации К*, отнесенных к диадному базису актуальной конфигурации.

Остановимся на геометрическом смысле приведенных выше тензоров градиентов скоростей перемещений. Рассмотрим две бе с-

этот член представляет собой относительную скорость той же ча с- тицы в конфигурации К*, компоненты которой отнесены к базису актуальной конфигурации Кt . Наконец, аналогично показывается,

что Le dr = dvKt ei dvK* eˆi , т.е. эта составляющая представляет с о-

бой разность скоростей той же частицы в конфигурации К t и в конфигурации К* (приведенную к базису актуальной конфигур а- ции).

Введенные соотношениями градиенты скоростей перемещений представляются разложением на симметричную (тензоры деформ а- ции скорости) и антисимметричную (тензоры вихря) составля ю- щие:

Следует отметить, что обе составляющие De и We содержат скорости упругих искажений решетки и вращения тела как целого, тогда как Wр описывает скорость вращения решетки за счет пластич е- ских сдвигов («полностью стесненная модель Тейлора»).

Введем меру Коши–Грина G* и тензор деформаций Коши– Грина C* [57] при использовании в качестве отсчетной конфигур а- ции К* (в анализируемой статье последний назван «решеточным тензором Грина):

298

где g – метрический (единичный) тензор, gˆ ij – его компоненты в ба-

зисе актуальной конфигурации. С использованием (9.41)1 , (9.43) и (9.45) нетрудно показать, что справедлива следующая связь:

которая потребуется в дальнейшем.

В геометрически нелинейной теории пластичности наряду с тензором напряжений Коши σ часто используется тензор напряже-

o

ний Кирхгоффа (или «взвешенный тензор Кирхгоффа») K = ρ ρˆ σ

o

(см. п.1.1.2), где ρ, ρˆ – плотность в отсчетной и актуальной конф и-

гурации соответственно. Заметим, что свертки K : D и σ : D определяют мощность напряжений на единицу объема соответственно в отсчетной и актуальной конфигурациях.

В работе полагается, что свободная энергия (Гельмгольца)

не зависит от пластических сдвигов и является функцией только С*. Мощность работы напряжений определяется соотношением

ния. Первый член правой ча сти характеризует скорость изменения свободной энергии Гельмгольца и может быть выражен через как

C : C , тогда с учетом (9.46) можно записать

как функции С*, то (9.49) можно трактовать как закон гиперупр у- гости (закон Гука с заменой линейной меры деформаций на нел и- нейную).

Далее вводится коротационная производная K r [57] тензора

Кирхгоффа K , ассоциированная с решеточным упругим спином

Wе :

299

Дифференцируя (9.49) по времени и подставляя в (9.50), с использованием (9.46)2 получаем

т.е., по сути, осуществляется переход к гипоупругому закону. К сожалению, авторам не удалось доказать правомочность такого п е- рехода, вероятно, он неверен (возможно, использовалось известное в тензорном анализе «цепное правило», справедливое только для сверток тензоров второго ранга, тогда как в данном соотношении фигурирует тензор четвертого ранга). Заметим, что запись первого члена правой части (9.51) в компонентах не меняет закона гипоупругости, имеет место просто усложнение записи.

В дальнейшем, заменой в (9.50) Wе =W–Wр и переходом к ко-

ротационной производной K r , ассоциированной с тензором (материального) вихря W, определяющее соотношение преобразуется к виду

K M((A)k ) M((A)k ) K γ(k ).

k

Наконец, заменяя Dе = D – Dр , а Dр выражая через скорости сдвигов, получаем ОС упруговязкопластичности, связывающее корот а-

ные ОС для решения кон кретных задач, следует определить закон для скоростей сдвигов, в качестве которого используется вязкопл а- стический закон (степенная зависимость скорости сдвига от сдв и- гового напряжения на каждой СС)

где а( k ) – так называемая «отсчетная скорость» (сдвига) (нетрудно видеть, что она равна ско рости сдвига при K (k ) = g(k ) ); g(k ) – функ-

ция упрочнения, зависящая от суммарного сдвига, накопленного на всех системах скольжения; m – показатель скоростной чувствительности монокристалла. Из (9.53) следует однозначная определенность скорости сдвига по любой СС, причем скорость сдвига

300