
Теория определяющих соотношений. Часть 2. Теория пластичности
.pdf
23) 2) Показать справедливость соотношений (4.7), (4.12).
24) 2) Получить систему неравенств (4.8) и построить круги Мора.
25) |
1) Показать, что величина τ |
S |
в критерии |
пластичности Треска ( |
|||||
|
|
|
|
|
|
|
|
|
|
max | σi 1 |
σi 2 | 2 τS ) – предел текучести при чистом сдвиге (см. упр. 1,2), а |
||||||||
|
|
|
|
|
3 |
|
|
|
|
величина |
S |
в критерии пластичности Мизеса ( |
(S |
S |
)2 |
2σ2 ) – предел |
|||
|
|
|
|
|
i |
i 1 |
|
S |
|
|
|
|
|
|
i 1 |
|
|
|
|
текучести при чистом растяжении. |
|
|
|
|
|
|
|||
26) |
2) Установить энергетический смысл условия пластичности Мизеса. |
||||||||
27)Для тонкостенного образца (см. рис. 1) определить условие для величин нагрузок F, M, p в момент выполнения критерия пластичности Треска, Мизеса.
28)2) Определить вид функции упрочнения f (εup ) из опыта на одноосное
растяжение, если кривая σ ε состоит из двух прямолинейных участков, тангенсы наклона которых к оси интенсивности деформации есть E1 , E2 , а
координата точки излома по оси напряжений есть σT .
29) 2) Определить вид функции упрочнения f (εu ) из опыта на одноосное растяжение для упругопластического материала с линейным упрочнением.
Параметры E1 , E2 , σT |
и коэффициент |
Пуассона |
для упругого |
|
деформирования известны. |
|
|
|
|
30) Шар |
со сферической |
полостью из упруго-пластического материала |
||
находится |
под действием |
внешнего pb |
и внутреннего |
давления pb . |
Геометрические центры шара и полости совпадают, радиус шара – b , радиус полости – a , a b . При какой разности давлений чисто упругое деформирование станет невозможным? В каком месте шара начнется развитие пластических деформаций?
31) 2) Упруго-пластический материал находится под сжимающей нагрузкой p , приложенной вдоль оси x1 , в условиях плоской деформации между двумя жесткими пластинами, нормальными оси x3 , так что σ22 0 , ε33 0 .
2) Трусов П.В. Механика сплошной среды: курс лекций. Ч. 3. Классические среды. –
Пермь: Изд-во ПГТУ, 1996. 142 стр.
321

Используя критерий Мизеса, определить величину нагрузки p и тензор малых деформаций в момент начала пластической деформации.
32) 1) Бесконечно длинная труба, имеющая внутренний радиус a и внешний радиус b , находится под действием внешнего pb и внутреннего давления pb .
При какой разности давлений упругое деформирование станет невозможным? В каком месте трубы начнется развитие пластических деформаций?
33)Цельный цилиндр радиусом R закручивается с моментом M . При какой величине момента упругое деформирование станет невозможным? В каком месте цилиндра начнется развитие пластических деформаций?
34)2) Проверить справедливость равенства э э = 23 e : e для случая связи
компонент векторов деформаций |
и компонент девиатора тензора |
деформаций в виде (5.3) . |
|
35) 2) Доказать взаимообратность матриц преобразований компонент девиатора тензора деформаций (напряжений) в компоненты векторов
деформаций (напряжений) и обратно: (5.2) (5.4), (5.3) |
(5.5). |
36) 2) Определить параметры кривизны и кручения в терминах компонент девиатора тензора малых деформаций.
37)Проверить (при необходимости – определить условия) выполнение аксиом Нолла для определяющих соотношений ТУПП (5.17)– (5.29).
38)Для изотропного полого шара из упруго-идеально-пластического материала, на который действует внутреннее давление p , найти поля
напряжений, деформаций и перемещений при использовании соотношений теории малых упругопластических деформаций.
39)Получить решение задачи простого сдвига для упруго-идеально- пластического тела по соотношениям теории малых упругопластических деформаций.
40)См. упр. 38 – аналогично для изотропно упрочняющегося тела с линейным и степенным законами упрочнения.
41)Траектория деформации (после установления) – окружность радиусом R , критерий пластичности выполняется. Полагая материал упруго-идеально- пластическим и используя соотношения для траектории малой кривизны
322
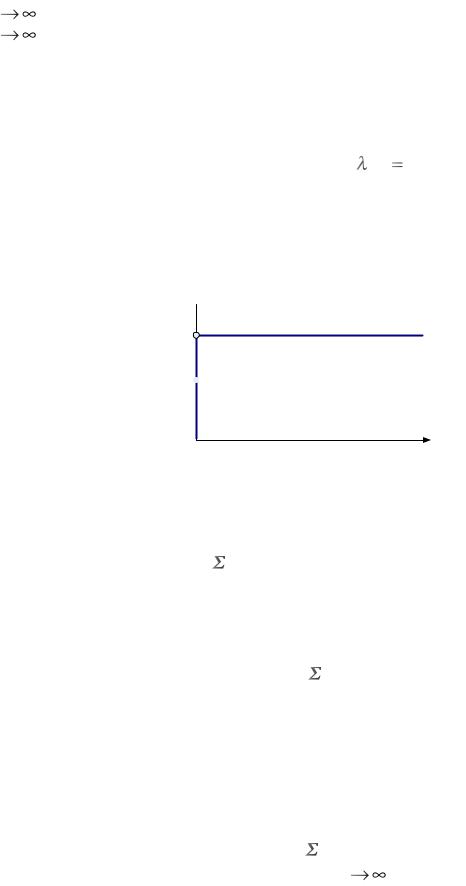
ТУПП, получить зависимость Σ(s) . Рассмотреть установившееся состояние (
s ). Каков должен быть радиус R , чтобы мощность напряжений при s была нулевой?
42)См. упр. 39 – аналогично для материала с линейным и степенным законами упрочнения.
43)См. упр. 39 – аналогично для случая использования соотношений для
траекторий средней кривизны в форме (5.20), ( s) const .
44)См. упр. 41 – аналогично для материала с линейным и степенным законами упрочнения.
45)Траектория деформации OABС изображена на рис. 3.
э2 
B |
C |
A
O |
э1 |
|
|
|
Рис. 3. Траектория деформации |
На участке ОА происходило упругое деформирование, в точке А выполнился критерий пластичности. Принимая материал упруго-идеально- пластическим, определить (s) , используя соответствующие соотношения
ТУПП.
46) Траектория деформации (после установления) – квадрат со стороной L , при этом критерий пластичности выполняется. Принимая материал упруго-
идеально-пластическим, определить |
(s) , используя соответствующие |
соотношения ТУПП. |
|
47)См. упр. 45 – аналогично для материала с линейным и степенным законами упрочнения.
48)Траектория деформации (после установления) – правильный n - угольник, вписанный в окружность радиусом R . Принимая материал упруго-
идеальнопластическим, определить |
(s) , |
используя соответствующие |
соотношения ТУПП. (Получается ли при n |
результат решения задачи |
|
(41)?) |
|
|
323

49) |
См. упр. 46 – аналогично для материала с упрочнением, Ф( s) |
const . |
|||||||||||
50) |
Принимая гипотезу компланарности, найти вид коэффициентов в |
||||||||||||
|
э A |
|
|
|
B ( |
|
|
|
|
|
|
|
|
разложении |
|
|
|
|
) , приняв |
( |
|
) |
L( 1, s) |
известной |
|||
|
|
|
|
|
|||||||||
|
|
|
Ф(s) |
Ф(s) |
|
Ф(s) |
|
|
|||||
функцией, |
1 – угол между векторами э и Σ , |
|
s – длина дуги траектории |
||||||||||
деформации, Ф(s) |
|
|
– функция упрочнения. |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
51)Проверить (при необходимости – определить условия) выполнение аксиом Нолла для определяющих соотношений одноповерхностных ТПТ с кинематическим упрочнением (6.1), (6.2),(6.5).
52)Для изотропного полого шара из упруго-пластического материала, на который действует внутреннее давление p , найти поля напряжений,
деформаций и перемещений при использовании соотношений ТПТ с различными законами кинематического упрочнения (см. табл. 6.1.).
53)Получить решение задачи простого сдвига для упруго-идеально- пластического тела по соотношениям ТПТ.
54)См. упр. 53 – аналогично с линейным и степенным законами изотропного упрочнения.
55)См. упр. 53 – аналогично с различными законами кинематического упрочнения (см. табл. 6.1.).
56)Траектория деформации – луч, начальное состояние – естественное. Полагая материал упруго-идеально-пластическим, определить траекторию
вектора напряжений и траекторию вектора остаточных микронапряжений ρ для одноповерхностных ТПТ с различными законами кинематического
упрочнения (табл. 6.1).
57) Траектория деформации представляет собой циклическое движение по отрезку (например, циклический процесс растяжения–сжатия). Полагая материал упруго-идеально-пластическим, определить траекторию вектора напряжений и траекторию вектора остаточных микронапряжений ρ для
одноповерхностных ТПТ с различными законами упрочнения (табл. 6.1).
58) Траектория деформации (после установления) – квадрат со стороной L , критерий пластичности выполнен. Полагая материал упруго-идеально- пластическим, определить траекторию вектора напряжений Σ и траекторию
324

вектора остаточных микронапряжений ρ для одноповерхностных ТПТ с различными законами упрочнения (табл. 6.1).
59) Траектория деформации (после установления) – окружность радиусом R , критерий пластичности выполнен. Полагая материал упруго-идеально- пластическим, определить траекторию вектора напряжений Σ и траекторию вектора остаточных микронапряжений ρ для одноповерхностных ТПТ с
различными законами упрочнения (табл. 6.1).
60)Построить ОС на основе структурной модели, соответствующей приведенной на рис. 6.2, с внедрением упругих элементов между элементами сухого трения.
61)См. упр. 56 – аналогично для двухповерхностной ТПТ в форме (6.19),
(6.20), (6.22).
62)См. упр. 56 – аналогично для двухповерхностной ТПТ в форме (6.19),
(6.20), (6.23).
63)См. упр. 57 – аналогично для двухповерхностной ТПТ в форме (6.19),
(6.20), (6.22).
64)См. упр. 57 – аналогично для двухповерхностной ТПТ в форме (6.19),
(6.20), (6.23).
65)См. упр. 58 – аналогично для двухповерхностной ТПТ в форме (6.19),
(6.20), (6.22).
66)См. упр. 58 – аналогично для двухповерхностной ТПТ в форме (6.19),
(6.20), (6.23).
67)Построить структурные модели, соответствующие гипотезам Фойгта, Рейсса, Кренера.
68)Проверить (при необходимости – определить условия) выполнение аксиом Нолла для определяющих соотношений ЭТП.
69) |
Показать, что (7.12), (7.13) можно представить в форме (7.1) с ядром |
J( z) |
E e αz и внутренним временем, определенным согласно (7.13). |
70) |
Показать, что при = 1 соотношения ЭТП сводятся к соотношениям |
ТПТ.
325

71) Траектория деформации – луч. Определить траекторию вектора напряжений , используя (7.12)-(7.13) при различных постоянных значениях параметра .
72) Траектория деформации – окружность радиуса R . Определить траекторию вектора напряжений , используя (7.12)–(7.13) при различных постоянных значениях параметра .
73) Траектория деформации (после установления) – правильный n - угольник, вписанный в окружность радиуса R . Определить траекторию вектора напряжений , используя (7.12)-(7.13) при различных постоянных значениях параметра .
74)См. упр. 71 – аналогично при = (s)=1-e-s.
75)См. упр. 72 – аналогично при = (s)=1-e-s.
76)См. упр. 73 – аналогично при = (s)=1-e-s.
77)Траектория деформации – циклически по отрезку. Определить траекторию вектора напряжений , используя (7.12)-(7.13) при различных
постоянных значениях параметра .
78) Для изотропного полого шара из упруго-идеально-пластического материала, на который действует внутреннее давление p , найти поля
напряжений, деформаций и перемещений при использовании соотношений ЭТП.
79)Получить решение задачи простого сдвига для упруго-идеально- пластического тела по соотношениям ЭТП.
80)См. упр. 79 – аналогично для изотропно упрочняющегося тела с линейным и степенным законами упрочнения.
81)Предложить обобщение соотношений ЭТП на геометрически нелинейный случай.
82) Показать, что первый инвариант линейной комбинации |
aiMi равен 0. |
83) Показать, что критерий Шмида соответствует критерию Треска для соответствующего сдвига.
326

С использованием построенных моделей проанализировать различные процессы деформирования.
328
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1.Аннин Б.Д. Поведение материалов в условиях сложного нагружения. / Б.Д. Аннин, В.М. Жигалкин – Новосибирск: Изд-во СО РАН, 1999.–342 с.
2.Белл Дж. Ф. Экспериментальные основы механики деформируемых твердых тел. Ч.1. Малые деформации (600 с.); Ч.2. Конечные деформации (432 с.)/ Дж. Ф. Белл – М.: Наука. Гл. ред. физ.-мат. лит, 1984.
3.Бондарь В.С. Неупругость. Варианты теории./ В.С. Бондарь – М.: ФИЗМАТЛИТ, 2004. –144 с.
4.Бородий М.В. Применение эндохронной теории пластичности для моделирования непропорционального повторно-переменного жесткого нагружения./ М.В. Бородий // Проблемы прочности. 1994. №5. С.3–10.
5.Вакуленко А.А. Связь микро- и макросвойств в упругопластиче-
ских средах./ А.А. Вакуленко // Итоги науки и техники. Сер. Механика деформируемого твердого тела. ВИНИТИ. 1991. №22. С.3–54.
6. Валанис К. Обоснование эндохронной теории пластичности методами механики сплошной среды./К. Валанис // Тр. ASME. Теоретические основы инженерных расчетов. 1984. Т.106. № 4. С.72–81.
7.Васин Р.А. Некоторые вопросы связи напряжений и деформаций при сложном нагружении/ Р.А. Васин // Упругость и неупругость. Вып.1. – М.: Изд-во МГУ, 1971. – С.59– 126.
8.Васин Р.А. Свойства функционалов пластичности у металлов, определяемые в экспериментах на двузвенных траекториях деформации./ Р.А. Васин // Упругость и неупругость. – М.: Изд-во МГУ, 1987. – С.115–127.
9.Васин Р.А. Об экспериментальном исследовании функционалов пластичности в теории упругопластических процессов./ Р.А. Васин // Пластичность и разрушение твердых тел. – М.: Изд-во МГУ, 1988. – С.40–
10.Васин Р.А. Определяющие соотношения теории пластичности./ Р.А. Васин // Итоги науки и техники. Сер. Механика деформируемого твердого тела. ВИНИТИ. 1990. №21. С.3–75.
11.Васин Р.А. Введение в механику сверхпластичности: В 2 ч./ Р.А. Васин, Ф.У. Еникеев – Уфа: Гилем, 1998. Ч.1. – 280 с.
12.Зубчанинов В.Г.Механика сплошных деформируемых сред./ В.Г. Зубчанинов – Тверь: Изд-во ТГТУ, ЧуДо,2000.– 703 с.
13.Зубчанинов В.Г. Основы теории упругости и пластичности./ В.Г. Зубчанинов – М.: Высшая школа, 1990. – 368 стр.
14.Ивлев Д.Д. Теория упрочняющегося пластического тела./ Д.Д. Ивлев, Г.И. Быковцев – М.: Наука. Гл. ред. физ.-мат. лит-ры. 1971. 232 стр.
329
15.Ильюшин А.А. О связи между напряжениями и малыми деформациями в механике сплошных сред./ А.А. Ильюшин // ПММ. 1954. Т. XVIII. Вып. 6. С.641–666.
16.Ильюшин А.А. Об основах общей математической теории пластичности. / А.А. Ильюшин //Вопросы теории пластичности. – М.: Изд-во АН СССР, 1961. – С.3–29.
17.Ильюшин А.А. Пластичность. Основы общей математической теории. / А.А. Ильюшин – М.: АН СССР, 1963.– 272 с.
18.Ильюшин А.А. Об одной модели, поясняющей аппроксимационный метод СН–ЭВМ в теории пластичности. / А.А. Ильюшин // Упругость и неупругость. Вып.1. – М.: Изд-во МГУ, 1971.– С. 52–58.
19.Ильюшин А.А. Пластичность. Ч.1. Упруго-пластические деформации. / А.А. Ильюшин – М.: Логос, 2004.– 388 с.
20.Ильюшин А.А. Труды (1946–1966). Т.2. Пластичность. / А.А. Ильюшин – М.: ФИЗМАТЛИТ, 2004.– 480 с.
21.Ишлинский А.Ю. Общая теория пластичности с линейным упрочнением./ А.Ю. Ишлинский // Украинский математический журнал. 1954. Т.6. №3. – С.314–325.
22.Кадашевич Ю.И. О различных тензорно–линейных соотношениях в теории пластичности./ Ю.И. Кадашевич // Исследования по упругости и пластичности. Л.: Изд-во ЛГУ, 1967. Вып. 6. – С.39–45.
23.Кадашевич Ю.И. Учет изменения скорости деформирования при построени определяющих уравнений неупругих материалов. / Ю.И. Кадашевич, В.С. Клеев Прикладные проблемы прочности и пластичности. Горький: Горьковский универс тет, 1981. № 18. – С. 20–23
24.Кадашевич Ю.И. О теории пластичности, не имеющей поверхности текучести/ Ю.И. Кадашевич, А.Н. Михайлов/ Ю.И. Кадашевич, А.Н. Михайлов // ДАН СССР. 1980. Т. 254. №3. С.574–576.
25.Кадашевич Ю.И. Вероятностный подход в эндохронных теориях пластичности./ Ю.И. Кадашевич, А.Б. Мосолов// Доклады АН СССР. 1988. Т.300. №5. С.1084–1086.
26.Кадашевич Ю.И. Эндохронные теории пластичности: основные положения, перспективы развития./ Ю.И. Кадашевич, А.Б. Мосолов // Изв. АН СССР. МТТ. 1989. №1. С.161–168.
27.Кадашевич Ю.И. Современное состояние эндохронной теории пластичности./ Ю.И. Кадашевич, А.Б. Мосолов// Проблемы прочности. 1991. №6. С.3–12.
28.Кадашевич Ю.И. Теория пластичности, учитывающая эффект Баушингера./ Ю.И. Кадашевич, В.В. Новожилов// Доклады АН СССР. 1957. Т.117. №4. С.586–588.
29.Кадашевич Ю.И. Теория пластичности, учитывающая остаточные микронапряжения./ Ю.И. Кадашевич, В.В. Новожилов// Прикладная математика и механика. 1958. Т.22. Вып.1. С.78–89.
330
