Теория определяющих соотношений. Часть 2. Теория пластичности

гим образом, C0 . При продолжающемся нагружении в положительном направлении оси S2 ИТН «захватывает» поверхность f0 и движется вместе с ней до достижении точки F1 ; пластическое деформирование на участке F0 F1 осуществляется с модулем пластичности C1 . До достижения точки F1 все поверхности f1,f2 ,...,fn остаются неподвижными. При достижении ИТН точки F1 и продолжающемся лучевом нагружении уже две поверхности, f0 и f1 , движутся вместе с ИТН поступательно прямолинейно вплоть до точки F2 . Деформирование на участке F1F2 осуществляется с пластическим модулем C2 , окружности f2 ,f3 ,...,fn остаются неподвижными. Аналогичным образом

можно описать последующее активное лучевое нагружение. На рис. 6.3, б изображено положение поверхностей, соответствующее достижению ИТН точки F3 .

Пусть начиная с этого момента осуществляется процесс разгрузки и нагружения в обратном направлении. При движении ИТН от точки F3 до точки

R0 (рис. 6.3, б) материал деформируется упруго, точке R0 соответствует на-

чало пластического деформирования в обратном направлении. Начиная с точки R0 , ИТН движется в отрицательном направлении оси S2 вместе с по-

верхностью f0 вплоть до касания окружности f1 в точке R1 . На этом этапе деформирования все остальные поверхности f1,f2 ,...,fn сохраняют положение, занимаемое ими в конце предыдущего участка активного нагружения. После достижения ИТН положения R1 дальнейшее деформирование до положения R 2 сопровождается совместным перемещением поверхностей f0 , f1 при неподвижных поверхностях f2 ,f3 ,...,fn ; деформирование на участке R1R2 осуществляется с пластическим модулем C2 . На рис. 6.3, в изображено положение поверхностей в момент достижения ИТН положения R 3 .

При формулировке определяющего соотношения полагается справедливым принцип градиентальности, причем при определении градиента используется последняя из поверхностей нагружения fk, вовлеченная в трансляцию в пространстве напряжений вместе с ИТН, и соответствующий ей пластический модуль C k+1.

– проекция бесконечно малого приращения девиатора напряжений на еди-

211

ничную нормаль к активной поверхности нагружения f; C – модуль упрочнения, являющийся обобщением тангенциального модуля, используемого в случае одноосного нагружения. Отметим, что в силу пропорциональности

перемещаться только поступательно, могут только касаться друг друга, последовательно вовлекая в движение поверхности с большими номерами. На любом участке активного пластического деформирования все предшествующие поверхности нагружения, «захваченные» при движении ИТН, касаются друг друга в точке текущего положения ИТН.

Рассмотрим случай, когда после нагружения до точки F3 (см. рис. 6.3б)) произошла частичная разгрузка до положения R0 ' , а затем осуществляется нагружение по лучу R0 ' R0 ' ' R1 ' R2 ' R3 ' R4 ' , параллельному оси S1 (рис. 6.4). После достижения ИТН положения R0 ' ' и продолжающегося нагружения вдоль R0 ' ' R4 ' поверхность f0 не может перемещаться ни вдоль единичной нормали n0 в точке R0 ' ' , ни вдоль луча R0 ' ' R4 ' , поскольку в этом случае она будет пересекать другие поверхности, что недопустимо. Конечная трансляция, приводящая к касанию окружностей f0 и f1 в точке R0 ' ' , расположенной на f0 , может быть осуществлена поступательным перемещением f0 на вектор R0''A1 , где A1 определяет положение внешней нормали n10 на поверхности f1 , совпадающей с n0 . Однако при этом будет нарушено другое условие: точка A1 не является местом расположения ИТН, поскольку траектория нагружения задана и определяется лучом R0 ' R4 ' . В связи с этим используется следующая схема: мгновенное перемещение поверхности f0 осуществляется вдоль R0''A1 , однако ИТН остается на поверхности f0 . Тогда

после бесконечно малого смещения поверхности f0 вдоль R0''A1 определяется новое положение R0 ' ' на поверхности f0 , одновременно принадлежащее лучу R0 ' R4 ' . Из рассмотрения рис.6.4 нетрудно видеть, что при этом угол между n0 и осью OS2 уменьшится. После этого определяется новое положение точки A1 , причем в силу вышесказанного угол F3O1A1 уменьшается на то же значение, на которое уменьшится угол F3O0R0 '' . В ходе бесконечно малых шагов происходит постепенное сближение положения R0 ' ' ИТН на f0 и соответствующей точки A1 на f1 . При этом точка R0 ' ' все время будет

212

оставаться на луче R0 ' R4 ' , в силу чего положение точки A1 на f1 будет при-

ближаться к указанному лучу. В конечном счете при переходе ИТН в положение R1 ' поверхности f0 и f1 будут касаться друг друга в этой точке.

Перейдем к математическому описанию движения поверхностей нагружения. Для этого достаточно рассмотреть процесс перемещения одной из поверхностей (например, fl ) до касания с поверхностью следующего уровня (

fl 1 , рис.6.5). Действительно, все поверхности с последующими номерами остаются неподвижными ( fl 1,fl 2 ,..,fn ).

Рис.6.4. Иллюстрация к модели З.Мруза (случай сложного нагружения в двумерном пространстве напряжений)

Описание движения ранее «захваченных» поверхностей ( f0 ,...,fl 1 ) мо-

жет быть осуществлено аналогично рассматриваемому случаю (напомним, что при активном нагружении все они должны касаться друг друга и поверхности fl в месте текущего положения ИТН). Ниже будет показано, что

положение поверхностей f0 ,...,fl 1 может быть установлено простыми соот-

ношениями. При этом отсутствует необходимость определения их положения в каждый момент нагружения, достаточно устанавливать их в момент начала разгрузки; при активном нагружении в соотношениях используются характеристики только последней из вовлеченных в движение поверхностей (в данном случае – fl ).

Рассматриваются две подобные поверхности нагружения fl и fl 1 , положение которых определяется центрами Ol и Ol 1 соответственно, устанавливаемые, в свою очередь, девиаторами остаточных микронапряжений ρl и

213

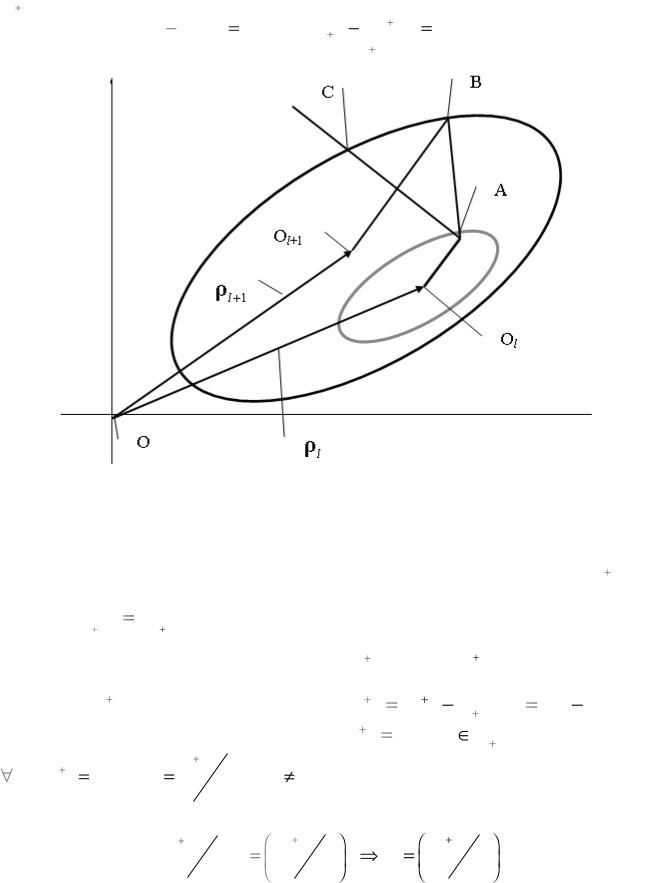
ρl 1 (рис. 6.5). Поверхности нагружения описываются уравнениями

где f – однородная функция порядка q, σ(0l ) ,σ(0l 1) – постоянные.

Рис. 6.5. Схема к описанию движения поверхностей текучести

Пусть изображающая точка лежит на поверхности fl в положении A, нагружение осуществляется вдоль луча AC. Тогда мгновенное перемещение поверхности fl осуществляется вдоль AB, где B – точка на поверхности fl 1 , имеющая одинаковое направление внешней нормали с внешней нормалью в

ределяется пересечением с поверхностью fl 1 прямой Ol 1B, параллельной Ol A . Обозначим девиаторы напряжений в точках A и B соответственно че-

откуда следует

214

Тогда dρl можно определить следующим образом:

где dμ – скалярный множитель, характеризующий величину смещения. В ча-

т.е. в этом случае мгновенная трансляция осуществляется вдоль Ol A . Отме-

тим, что в этом частном случае закон трансляции (6.14) совпадает с предложенным Г. Циглером (1959г.) законом для определения остаточных микронапряжений при произвольном нагружении с использованием одноповерхностной теории пластического течения:

dρ dμ S ρ .

Таким образом, в этом законе полагается, что смещение поверхности текучести осуществляется вдоль направления, связывающего центр поверхности текучести и ИТН.

Как уже отмечалось ранее, движение ИТН задано условиями нагружения. Для рассматриваемого случая, например, ИТН должна находиться на прямой AC, не покидая при этом поверхность нагружения fl . Иначе говоря, t ИТН участвует одновременно в двух мгновенных движениях – определяемом собственно нагружением ( dS ) и движением поверхности fl ( dρl ). По

аналогии с кинематикой сложного движения точки, рассматривая последнее как «переносное» движение, первое – как «абсолютное», для сохранения по-

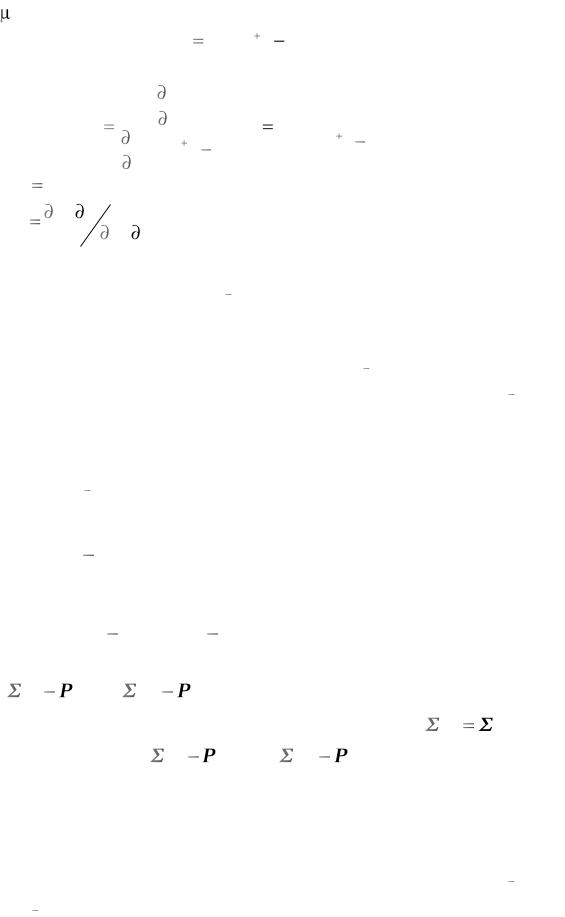
Соотношение (6.15) используется для определения скалярного множителя d . Для этого запишем вначале (6.13) в виде:

оставаться в контакте с поверхностью fl , причем общая точка контакта совпадает с текущим положением ИТН. Очевидно, что данное обстоятельство обусловливает смещение поверхностей f0 , f1 ,..., fl 1 относительно fl .

Отметим, что положение внутренних поверхностей f0 ,f1,...,fl 1 относительно fl при активном нагружении определяется в каждый момент процесса

простыми соотношениями. Действительно, в силу подобия поверхностей нагружения и в силу их выпуклости нетрудно заметить, что центры поверхностей f0 ,f1,...,fl 1 расположены на прямой Ol A . Данный факт следует из того,

что для выпуклой и гладкой поверхности ориентация внешней нормали полностью и однозначно определяется положением точки на поверхности, т.е.

тензором S(k ) ρk для любой поверхности fk . Поскольку в точке касания внешние нормали касающихся поверхностей fk и fm должны совпадать, а сами подобные поверхности движутся относительно друг друга поступательно, то тензоры S(k ) ρk , S(m) ρm должны быть пропорциональны. В векторном пространстве напряжений это означает, что соответствующие векто-

прямой, что и требовалось показать. Заметим, что в случае не строго выпуклых поверхностей (например, для поверхностей Треска–Сен-Венана) данное свойство также сохраняется, что следует из процедуры построения конфигурации семейства поверхностей нагружения.

Из приведенного свойства следует, что положение центра Ol 1 поверхности fl 1 , касающейся поверхности fl в точке S(l ) , может быть определено

216

соотношением

f0 ,f1,...,fl . При этом общая точка контакта находится постоянно в месте расположения ИТН и все центры O0 ,O1,...,Ol 1 расположены на одной прямой, соединяющей положение ИТН с центром Ol 1 .

Отметим, что все указанные выше положения и соотношения сохраняются в любом подпространстве пространства (5) . При этом, если нагружение осуществляется таким образом, что ненулевыми будут только некоторые компоненты девиатора S , то отличными от нуля будут только соответст-

вующие компоненты девиатора остаточных микронапряжений ρi , i 0, n всех поверхностей f0 ,...,fn .

Предполагаемая модель может быть обобщена на случай изменения

ний структуры и соотношений. Из экспериментов известно, что в процессе нагружения поверхность f0 может уменьшаться по размерам, тогда как ос-

симости используются эксперименты на циклическое нагружение. Последующее развитие многоповерхностной теории течения связано в

значительной мере с различными модификациями предложенной З.Мрузом модели. «Центр тяжести» исследований лежит в установлении законов перемещения поверхностей нагружения, их числа и размеров. При определении числа поверхностей возникают два предельных случая: n 2 и n . Наиболее широко применяемыми в последние 10–20 лет является двухповерхностные модификации модели Мруза. Особенно часто они используются для описания сложного (непропорционального) циклического нагружения. Остановимся вкратце на моделях данного типа.

В этом случае вводится поверхность f0 , отделяющая область упругого

деформирования от пластической зоны и называемая разными авторами

внутренней поверхностью, поверхностью текучести или поверхностью нагружения. Поверхность f0 в течение всего процесса нагружения не может

выходить за границы поверхности f1 , называемой внешней поверхностью,

граничной поверхностью или предельной поверхностью. Далее для f0 бу-

дем использовать термин «поверхность текучести», а для f1 – «предельная поверхность». Если в процессе активного нагружения ИТН находится в по-

217

A' на поверхности f1 , имеющую одинаковую единичную внешнюю нормаль,

Одну из первых двухповерхностных теорий предложили Я.Дафалиас и Е. Попов (1975). Система уравнений, определяющих пластическое деформирование, движение и изменение размеров поверхности текучести и предельной поверхности имеет вид

ются из экспериментов (вообще говоря, при сложном циклическом нагружении). При формулировке теории авторы сознательно оставили незамкнутой систему соотношений (6.21) для определения S',ρ0 ,ρ1 , что позволяет в ши-

роких пределах варьировать законы изменения поверхностей f0 и f1 . Так,

Ченгом и Ли (1983) предложена следующая конкретизация предлагаемых соотношений:

Более общий случай конкретизации соотношений (6.21) приведен в ра-

боте [30]:

Наличие большого числа материальных постоянных в последних соотношениях позволяют более точно описать экспериментальные данные, приводя, однако, к потребности более сложных экспериментов, чем в классических теориях пластического течения.

Следует отметить, что работы в направлении построения новых вариантов двухповерхностных теорий продолжаются (например, для описания сложного («непропорционального») циклического нагружения, что требует введения дополнительных параметров, характеризующих сложность нагру-

218

жения [72, 73]), поэтому представленный здесь краткий обзор теорий этого класса, конечно, не является сколь-нибудь полным. Впрочем, авторы и не ставили такой цели, главным является ознакомление с существующими «ветвями» и направлениями развития классической теории пластического течения.

219

О статистических теориях пластичности

Для большинства материалов, поведение которых описывается теми или иными теориями МДТТ на макроуровне, по мере углубления в микромир характерно выявление микроэлементов материала, обладающих примерно одинаковыми законами эволюции микроструктуры, механизмами деформирования, относительно стабильными физическими характеристиками. В связи с этим в МДТТ (и МСС в целом) одним из наиболее интенсивно развивающихся и, вероятно, перспективных направлений построения определяющих соотношений является статистический подход. Согласно указанному подходу выделяются микроструктурные элементы исследуемого материала, поведение которых описывается однотипными законами (по возможности – простыми), с минимально потребным количеством физических характеристик. Затем для достаточно большой совокупности микроструктурных элементов, составляющих представительный объем материала (в макросмысле), осуществляется статистическое осреднение.

Статистический подход до настоящего времени достаточно успешно применяется в теории упругости, в первую очередь – для композиционных материалов. В последнее время предпринимаются энергичные попытки применить его в теории пластичности, ряд из них следует признать достаточно успешными для сегодняшнего состояния теории пластичности. Однако, как отмечают авторы монографии [55], в настоящее время не представляется возможным достичь в теории пластичности хотя бы того же уровня строгости описания, как в теории упругости. Основным «камнем преткновения» является необходимость при построении статистической теории пластичности поликристаллов (или любой другой «теории неупругости») учитывать не только статистику упругих свойств зерен (в первую очередь – стохастическую ориентацию анизотропных зерен, субзерен), но и статистику различного рода дефектов (см. гл. 3).

В связи с этим в [55] предлагается так называемый квазистатистиче-

ский вариант теории пластичности, «…в котором при отказе от точного осреднения анизотропии кристаллитов, точного осреднения условий их взаимодействия и точного учета механических свойств отдельных кристаллитов тем не менее делается попытка уловить статистический характер процесса пластического деформирования» [55, с.26]. В рассматриваемой работе все многообразие случайных факторов (ориентации анизотропных (как по упругим, так и пластическим свойствам) зерен и субзерен, микроструктуры, включая дислокационные субструктуры, распределения точечных дефектов и т.д.) предлагается учитывать за счет статистического распределения предела текучести в элементах, совокупностью которых представляется поликристалл. В то же время разработанная теория [55] позволяет моделировать основные особенности поведения материалов даже при описании достаточно тонких эффектов. В связи с этим остановимся на этой теории несколько подробнее.

220