Теория определяющих соотношений. Часть 2. Теория пластичности

вариационном исчислении называются двойственными (друг другу): из одного с помощью так называемого преобразования Лежа н- дра следует другой, и наоборот (см., например, [40]).

Заметим, что в отличие от предположения Тейлора о том, что деформация реализуется сдвигом не более чем по пяти системам скольжения, здесь такого предположения не вводится, число а к- тивных систем скольжения ограничивается только числом возмо ж- ных кристаллографических систем, что еще более усугубляет пр о- блему неоднозначности определения сдвигов. Нетрудно видеть, что принцип минимума сдвига не позволяет определить единственный набор систем скольжения, он обеспечивает только «отбр а- ковку» векторов сдвига, не являющихся физически возможными.

Поликристаллический агрегат

Хотя в физической теории пластичности большое внимание уделяется построению моделей монокристаллов, главной задачей является формулировка конститутивной модели представительного объема макроуровня для поликристаллических материалов, без ч е- го невозможна постановка и решение практически важных краевых задач МДТТ. В связи с этим нем инуемо встают вопросы о перех о- де от переменных и соотношений микроуровня (в рассматрива е- мых моделях точнее надо говорить о мезоуровне) к переменным и соотношениям макроуровня, о процедурах идентификации и вер и- фикации разрабатываемых моделей. При этом одним из важных компонентов модели становится принимаемая процедура осредн е- ния.

Физическая теория пластичности в различных ее модифик а- циях в значительной мере опирается на макроэксперименты. В ч а- стности, из макроэкспериментов определяются физические пар а- метры (или часть из них), фигурирующие в описании микродефо р- мирования. Правильность основных положений ФТП проверяется в конечном счете также в опытах на макрообразцах. В связи с выш е- сказанным в замкнутой ФТП должны присутствовать подходы и соотношения, позволяющие связывать микро - и макропараметры.

При проведении экспериментов и интерпретации результатов в рассмотрение входят напряжения и деформации, осредненные по большому числу микроэлементов (зерен). Понятно, что интерпр е- тация результатов макроэкспериментов с позиций ФТП существенным образом связана с принимаемой процедурой осреднения. Ниже рассматриваются некоторые аспекты принятого в теории Бишопа–Хилла подхода к осреднению, опирающегося на две о с- новные гипотезы о связи микро - и макропараметров.

Измерения макропеременных осуществляются на таких объ е-

мах, что распределение ориентаций и упрочнения зерен в ра з-

261

личных объемах отличаются несущественно . Иначе говоря, об-

разец полагается однородным в макросмысле. Следует отметить, что это не исключает из рассмотрения ан изотропные материалы, поскольку распределение ориентаций не обязательно равномерное, могут реализовываться случаи преимущественной ориентации в определенных направлениях.

Вдальнейшем наименьший объем, обладающий подобными свойствами, будет называться «еди ничным» кубом (имеющим в действительности форму куба и единичные ребра).

Отсутствует корреляция между микроскопическими н а- пряжениями и положением на плоскости произвольного сеч е-

ния «единичной» площади. Данное предположение позволяет представить результирую щую микронапряжений на такой едини ч- ной площади как одиночную силу, приложенную в центре площа д- ки. Выбирая далее декартову ортогональную систему координат, по компонентам определенной таким образом силы нетрудно п о- лучить компоненты тензора макронапряжений, причем последний будет симметричным.

Вслучае, если корреляция между микронапряжениями и п о- ложением в единичном сечении существует, тензор микронапр я- жений не обязательно симметричный. В этом случае уравнение б а- ланса момента количества движения отличается о т классического,

врассмотрение необходимо вводить тензор моментных напряж е- ний. Иначе говоря, от классического континуума следует перех о- дить к обобщенному (например, континууму Коссера). Заметим, что подобное определение напряжений возможно на различных масштабных уровнях, включая используемый в некоторых вариа н- тах ФТП так называемый «атомный» (представительный объем

атомного уровня можно определить как объем совершенной кр и- сталлической решетки, содержащей 10 3 –106 атомов).

Рассмотрим связь кинематических характеристик микро- и макроуровней, опираясь на геометрический смысл компонент те н- зора малых деформаций. Будем обозначать через u, ε, σ микроско-

пические перемещения, деформации и напряжения, соответству ю- щие макропеременные будем обознач ать аналогичными символами с введением знака осреднения < >. Тогда приращение тензора м а- лых деформаций для «единичного куба» можно определить сл е- дующим образом:

где n – единичная внешняя нормаль к поверхности «единичного куба», S – его поверхность.

262

В случае если микроскопические перемещения принимаются непрерывными функциями пространственных координат, из (8.20) следует

V

где интегрирование ведется по объему единичного куба. Отметим, что в случае произвольных («не нормализованных») размеров представительного объема правые части (8.20) и (8.21) следует делить соответственно на S и V (будем полагать при этом, что представительный макрообъем имеет форму куба).

Следует подчеркнуть, что микропараметры представляют с о- бой некоторые осредненные величины по подобъемам представ и- тельных микрообъемов. Иначе говоря, и на микроуровне осущес т- влен переход к континууму.

Элементарная работа, совершаемая микронапряжениями в элементарном кубе представительного макрообъема, определяется соотношением

вторая часть соотношения справедлива в случае непрерывности полей микроперемещений и выполнени я на микроуровне однородного условия равновесия. Заметим, что компоненты микронапр я- жений не обязательно должны быть непрерывными на произвол ь- ных поверхностях (например, границах зерен) . Для выполнения условий равновесия должны быть непрерывны только результ и- рующие распределенные нагрузки на таких поверхностях.

В дополнение к двум предыдущим принимается гипотеза об отсутствии корреляции между рас пределением любых компонент микронапряжений и любыми компонентами микроперемещений в любом сечении единичной площади (в единичном кубе).

Отсутствие корреляции может быть косвенно подтверждено тем фактом, что резкие увеличения значений напряжений соотве т- ствуют местам расположения барьеров, стыкам зерен и т.д., тогда как резкие изменения микроперемещений реализуются на криста л- лографических системах, свободных от подобных препятствий.

Остановимся на этой гипотезе несколько подробнее. Напо м- ним, что для произвольных осредняемых случайных параметров A, B обычно принимается следующее разложение:

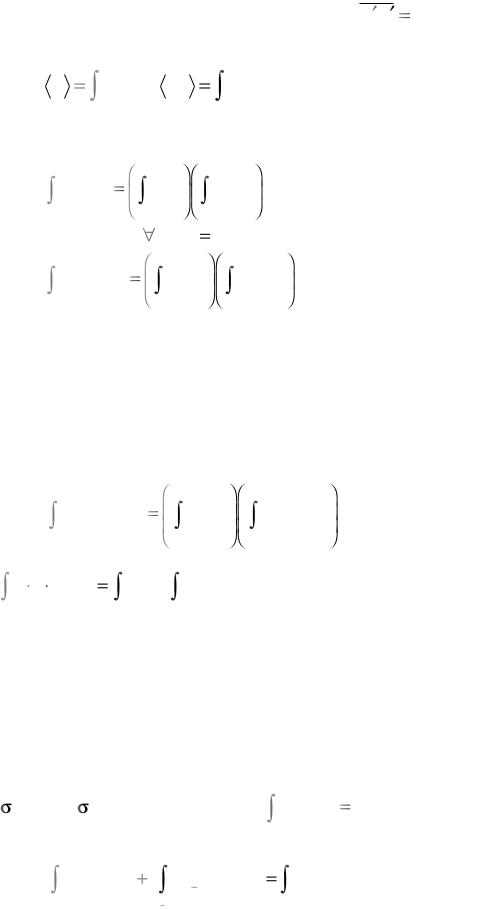
величинами A и B означает, что для осциллирующих составля ю-

щих можно принять следующее равенство: A B 0 .

В модели Бишопа–Хилла осреднение производится по ед и-

В частности, последнее соотношение элементарно выполн я- ется, когда напряжения или деформации однородны в рассматр и- ваемом единичном кубе (т.е. в условиях справедливости гипотез Рейсса или Фойгта). Заметим, что (8.24)–(8.25) получены для произвольной площадки единичной площади. Переходя в (8.25) к интегрированию по граням единичного куба, полагая j = k и домножая левую и правую части (8.25) на ni , суммируя по повторяющимся индексам, приходим к соотношению

где p – номер грани единичного куба.

Расположим куб ребрами вдоль осей декартовой ортогональной системы координат; номера граней в (8.26) и индексы для внешних нормалей вдоль осей xp и в противоположном направлении обозначим через p и (–p) соответственно. В силу условий ра в- новесия, выполняемых для представительного макрообъема (н а- помним, что рассмотрение ведется именно для представительного объема материала первого порядка [61, 62]), компоненты напряж е-

ний < >p q = < >( – p ) q ; кроме того, σ pq dS σ pq . Второй сомножи-

S p

тель правой части (8.26) отличен от нуля только для i = p (np + 1 =

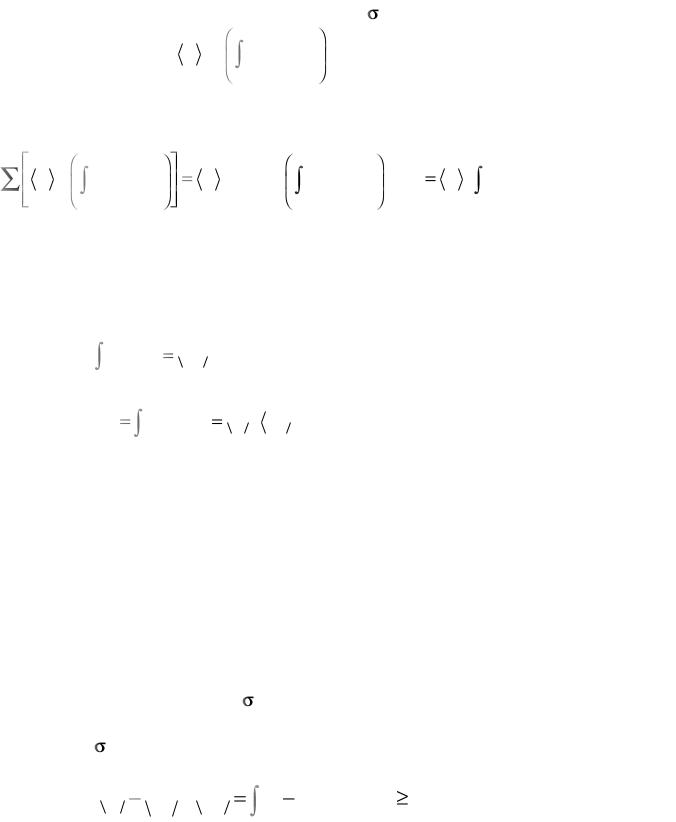
единичного куба. Таким образом, для членов с номерами p и (–p), вынося в качестве общего множителя < >p q , получаем, что правая

и пробегающего значения от 1 до 3 индекса q, по которому осуществляется суммирование. Просуммируем последнее соотношение по p:

Читателю рекомендуется самостоятельно проверить справе д- ливость данного соотношения вычислениями «справа налево» с учетом свойства np = 1, np + 1 = np + 2 = 0 на Sp .

Заметим, что без изменения результата подынтегральное в ы- ражение второго интеграла правой части (8.28) можно симметризовать. Тогда в соответствии с (8.20) имеем:

ndu dS dε . (8.29)

S

Таким образом, из (8.22) с учетом (8.28) и (8.29) получаем dA σ : dε dV σ : dε . (8.30)

V

Следует отметить, что при доказательстве (8.30) мы непосредственно исходили из (8.23). В то же время доказательство можно существенно упростить, если учесть, что в модели Бишопа – Хилла принята гипотеза Фойгта; по существу, оно сводится к у т- верждению об идентичности осреднения тензора напряжений по объему и (8.23)1 , доказательство которого предоставляет ся читателю.

С использованием последнего соотношения может быть док а-

зан принцип максимума работы для пластического поликр и-

сталла на основе принципа максимума для монокристалла, не прибегая при этом к понятию поверхности текучести поликриста л- ла. Действительно, пусть * – микронапряжения, не нарушающие условия текучести и удовлетворяющие однородному условию ра в- новесия, < *> – осредненные напряжения. Тогда в соответствии с

(8.30) и (8.17) имеем

σσ* : dε σ σ* : dε dV 0 , (8.31)

V

что и требовалось показать.

Аналогично доказывается принцип минимума сдвига для поликристалла. Пусть du и du* – непрерывные с непрерывными первыми производными поля перемещений, удовлетворяющие у с-

265

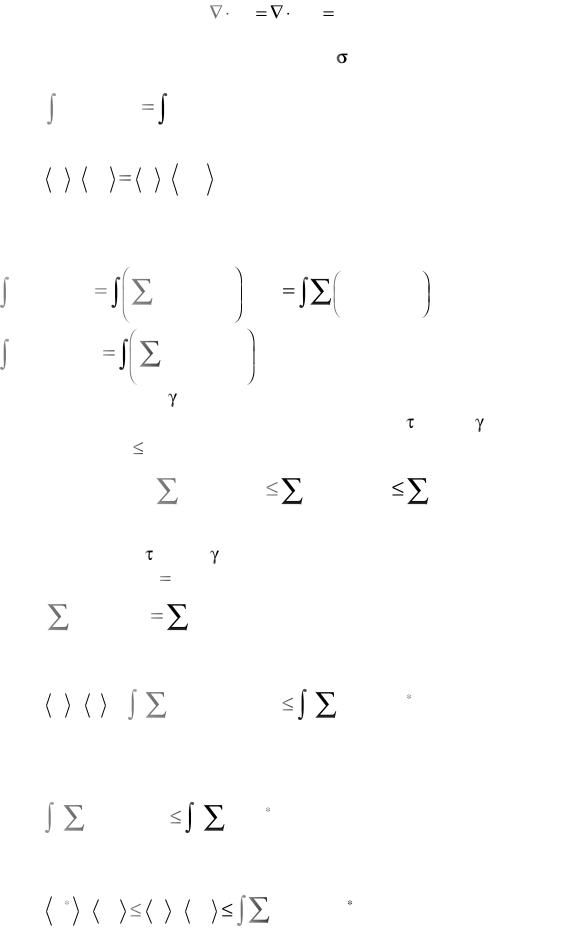
ловию сохранения объема ( du du* 0 ), имеющие одинаковые значения на поверхности единичного куба. Полагаем, что du ассоциировано с тензором микронапряжений , удовлетворяющих ус-

Указанные соотношения легко получа ются с использованием (8.28)– (8.29) с учетом равенства du и du* на поверхности единичного куба. При этом справедливы следующие равенства:

по агрегату, получаем принцип минимума сдвига для поликр и- сталла:

Кроме того, справедливо неравенство:

где d * соответствует некоторому перемещению du*. Напомним, что принципы максимума работы и минимума сдвига являются двойственными [40], и в этом смысле эквивалентны друг другу, один следует из другого.

Как следует из последних результатов, принцип максимума работы справедлив для агрегата из монокристаллических зерен в предположении, что деформирование в каждом из них ос уществляется сдвигом по определенным системам скольжения. Тогда из р а- нее сформулированного (без доказательства) утверждения следует, что может быть построен пластический потенциал, совпадающий с функцией текучести. Но тем самым решается в принципе вопрос об установлении определяющих соотношений в виде принципа градиентальности. Открытым остается только вопрос о величине скалярного множителя в законе градиентальности.

Построение функции текучести связано с определенными сложностями. Остановимся вначале на оц енках для частного случая изотропии в ориентации зерен и отсутствия эффекта Бауши н- гера. В этом случае можно показать, что поверхность текучести располагается между двумя цилиндрическими поверхностями. О т- метим, что в силу независимости условия текучести от шаровой части достаточно определить направляющую цилиндра на деви а- торной плоскости, для чего в каждом направлении в этой плоск о- сти следует определить расстояние от «начала координат» S = 0 (от гидростатической оси, равнонаклоненной к главным осям те н- зора напряжений) до точки начала текучести.

Получим вначале оценку «снизу», т.е. определим повер х- ность, ограничивающую поверхность текучести «изнутри». Пре д- положим, что напряженное состояние в рассматриваемом агрегате однородно, < > = , <S> = S (т.е., по существу, используется гипотеза Рейсса). Заметим, что в силу изохоричности деформаций замена в приведенных выше соотношениях (8.37), (8.38) тензора напряжений на девиатор напряжений не изменяет справедливости полученных неравенств.

Введем направляющий тензор r = <S>/ |<S>|, |<S>| = (<S>:<S>)1 / 2 . Для каждого из заданных направлений будем выб и- рать «допустимые», «пробные» микронапряжения S* таким образом, что они приводят к текучести только в одной системе скол ь- жения (в «слабейшем звене» агрегата). Иначе говоря, для всего а г- регата зерен отыскивается (при известной ориентации зерен и з а- данного направляющего тензора r ) СС с наибольшим фактором

267

Шмида. Допустимые напряжения для заданного направления о п- ределим в виде S* = λ*r, тем самым сводя задачу к определению скалярного множителя λ *, который вычисляется из условия дост и- жения критического напряжения в «слабейшем звене» (подобно тому, как это делается в модели Закса). При этом в силу принятого предположения <S* > = S* . Из (8.37) имеем

т.е. для каждого из направлений r модуль действительных напряжений не меньше величины λ *, определяемой критическим напр я- жением сдвига на рассматриваемом этапе нагружения (напомним, что критические напряжения полагаются здесь одинаковыми во всех системах скольжения).

Отметим, что, вообще говоря, λ * может зависеть от направления в девиаторной плоскости. В этом случае следует определить наименьшее λ * для всех r и можно построить круговой цилиндр с направляющей |< S>| = λ* = const, ограничивающий «изнутри» поверхность текучести. Однако в случае одинаковых значений с во всех системах скольжения и равномерного закона распределения ориентации зерен можно с большой степенью достоверности пре д- положить, что λ * не зависит от направляющего тензора r (заметим, что существует строгое доказательство независимости в модели Бишопа-Хилла величины модуля девиатора напряжений, соотве т- ствующей началу текучести, о т направления r).

Теперь получим оценку «сверху». Рассмотрим определение поверхности текучести в предположении однородного распредел е-

|<S>|. Выбрав произвольное направление r на девиаторной плоскости, рассмотрим «пробные» деформации d *, соответствующие активному нагружению, т.е. < S>:<d *> > 0. Пусть d ( i ) * – векторы сдвига в i-м зерне, эквивалентные d ( i ) * = d *, т.е.d ( k) *– геометрически возможные векторы сдвига (различные, вообще говоря, в разных зернах). Введем величину * следующим соотношением

r:dε

268

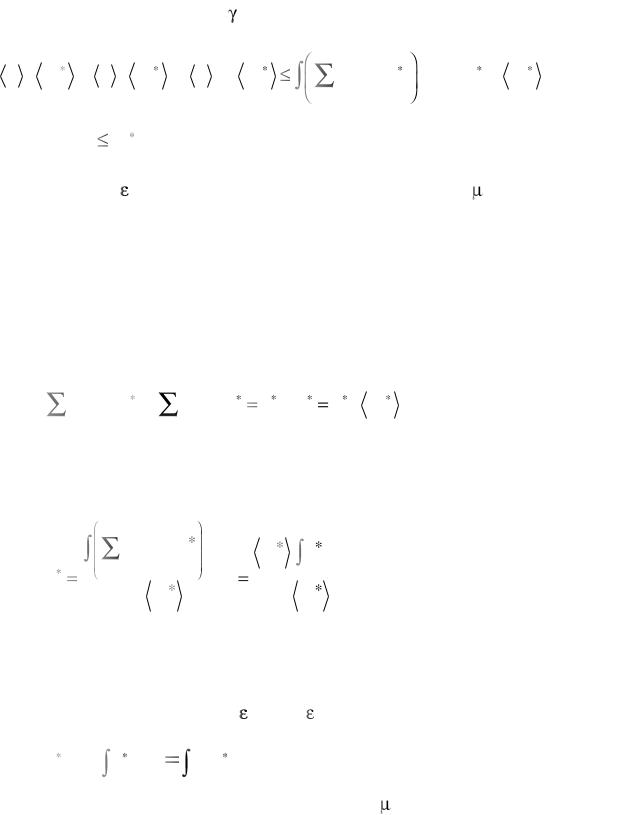
где зависимость от зерен входит через координаты, от которых в общем случае зависят и d ( k ) *; интегрирование осуществляется по объему единичного куба. В соответствии с (8.38) имеем

силу (8.35) реализуется на физически допустимых полях сдвигов

имеющих одинаковую деформацию). Полагая далее, что d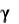 – геометрически и физически допустимые векторы сдвига в i-х зернах, 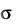– напряжения, обеспечивающие эти сдвиги в i-х зернах, для каждого из зерен (опуская обозначения номеров зерен) пол у- чаем:

Последнее соотношение справедливо для каждого отдельного кр и- сталла (зерна) и обеспечивает минимальное значение числителю (8.41) на множестве геометрически возможных сдвигов. Суммируя по всем зернам, приходим к соотношению

С учетом принципа градиентальности и того, что искомая ограничивающая поверхность текучести является круговым цили н- дром, тензор приращен ий деформаций для обеспечения макс и- мальности знаменателя следует направить вдоль девиатора дейс т- вительных напряжений, т.е. < d *> = d * r. Тогда из (8.43) следует (с учетом r:r = 1)

Таким образом, радиус направляющей * , ограничивающей поверхности текучести «сверху», определяется как работа, которая должна быть произведена над всеми зернами однородной ориент а- ции, на которые расщепляется единичный куб, и каждая из кот о- рых по отдельности испытывает деформации r.

269

Геометрическое место точек действительной поверхности текучести, таким образом, определяются неравенствами

тельной поверхности можно принять любую из ограничивающих, <S> = λ* или |<S>| = *. Однако в общем случае для применения теории Бишопа–Хилла к решению конкретных задач теории пл а- стичности требуется построение поверхности текучести, которое замыкает процедуру установления определяющих соотношений. Действительно, если поверхность текучести будет определена, для установления ОС достаточно воспользоваться ассоциированным законом течения. В связи с выш есказанным представляется целесообразным остановиться более детально на процедуре построения функции текучести монокристалла.

Здесь будут использованы упомянутые выше свойства неко р- релированности полей микронапряжений и микродеформаций. Р а- нее (см. уравнение (8.30)) показано, что для микронапряжений , удовлетворяющих однородному уравнению равновесия (в дал ь- нейшем для краткости такие напряжения будем называть равн о- весными) и произвольного тензора микродеформаций d в предположении существования поля перемещений du, такого, что d= ½ ( du+ duT ), и отсутствия корреляции между и du на любой единичной площадке, справедливо соотношение:

σ : dε dV = σ : dε .

V

Интегрирование в последнем соотношении ведется по объему единичного куба. Очевидно, что тензор приращений осредненных деформаций <d > также можно считать некоррелированным с те н- зором микронапряжений; тогда можно записать следующие соотношения:

V

где тензор напряжений – тот же самый, т.е. равновесный. Представим теперь агрегат, состоящий из отдельных свобо д-

ных зерен с присущими каждому из них однородными ориент а- циями и упрочнением, которые они имели в поликристалле. Пусть * – микронапряжения, которые в каждом из свободных зерен производят деформацию <d >, одинаковую для всех зерен. Понятно, что в общем случае (произвольной ориентации и упрочнения з е- рен) напряжения * не являются равновесными и отличаются от