Теория определяющих соотношений. Часть 2. Теория пластичности
.pdf
LA и GC. Для варианта ε11/ε22 5.33 приведены результаты расчета суммарной скорости сдвигов как функции напряжения σ11 и времени. Для обеих моделей при σ11 270 МПа и 285 МПа наблюдаются осцилляции суммарной скорости сдвига. Ав-
торы связывают это с неустойчивостью алгоритма в окрестности точек активизации вторичных СС. Проведено также сопоставление номеров четырех первичных и вторичных активируемых систем скольжения и накопленных сдвигов на них; за исключением
нагружения по траектории ε11/ε22 |
0.95 , где в модели GC не активировалась ни од- |
на из вторичных систем, соответствие результатов следует признать удовлетворительным, что обусловлено некоторым отличием траекторий нагружения (в модели LA в от-
личие от модели GC напряжение σ |
достигало в момент активизации вторичных СС |
11 |
|
значения 0). Аналогичное удовлетворительное соответствие получено для программ нагружения растяжение–сдвиг.
К сожалению, авторы не обсуждают, каким образом в упругопластической модели по предписанной деформации могут быть определены сдвиги в восьми системах скольжения. В плоском случае, анализируемом в данной работе, возможно одновременное определение не более трех скоростей сдвигов (даже при работе с полными напряжениями), в объемном – не более шести. Возможно, в статье речь идет о СС, активированных в течение всей истории нагружения.
Весьма подробно вопросы построения и применения физических моделей упруговязкопластичности для описания поведения поликристаллов в широком диапазоне скоростей деформации (10-3–102 с-1) при больших деформациях (порядка 100%) и относительно низких гомологических температурах (Тг<0.3) рассмотрены в статье [Д4]. Как и в большинстве рассмотренных выше работ, использовано мультипликативное разложение градиента места и ОС анизотропной гиперупругости (с учетом температурной деформации), в котором в качестве мер напряженного и деформированного состояния приняты соответственно второй тензор Пиола–Кирхгоффа и тензор деформаций Коши–Грина, определенные в терминах разгруженной конфигурации.
Пластическое деформирование полагается реализующимся скольжением краевых дислокаций. Следует отметить, что, как и во многих других работах последнего десятилетнего периода, закон вязкопластичности выводится на основе уравнения Орована:
|
γ(k ) = ρ(k )bv (k ) |
τ(k ) , τ(k ) , θ |
, |
, |
(9.69) |
|
|
m |
c |
|
|
|
|
|
|
|
|
|
k |
|
где ρ(k ) |
– плотность мобильных дислокаций, |
v (k ) – средняя скорость движения дисло- |
||||
m |
|
|
|
|
|
|
каций в k-й СС, причем v (k ) равна нулю при |
τ(k ) |
< τ(k ) |
. Критическое напряжение |
|||
|
|
|
|
|
c |
|
сдвига полагается равным сумме двух составляющих: сопротивления близкодействующих барьеров, которые могут быть преодолены за счет термических флуктуаций даже при напряжениях ниже барьера Пайерлса–Набарро (называемого термической состав-
ляющей) τ(ctk ) и сопротивления дальнодействующих барьеров (называемого атермиче-
ской составляющей) τ(cak ) (см., например, [Д14]). Для модуля средней скорости движения дислокаций принимается соотношение
311
|
|
|
|
|
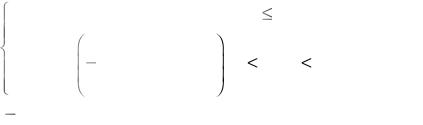
0 |
|
Δτ(k ) |
0, |
||||
|
v (k ) |
|
= |
|
|
|
|
|
ψ(k ) Δτ(k ) , τ(k ) |
|
(9.70) |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
l (k ) ν exp |
ct |
0 |
Δτ(k ) τ(k ) , |
||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
k θ |
|
ct |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
где Δτ(k ) = |
τ(k ) |
|
τ(k ) , |
l |
(k ) – средняя длина свободного пробега дислокаций, ν – ха- |
|||||||
|
|
|
|
|
|
|
ca |
|
|
|
||
рактеристический частотный параметр (порядка 1012 с-1), ψ(k ) – свободная энтальпия ак-
тивации (или свободная энергия активации Гиббса); направление движения совпадает с направлением сдвиговых напряжений. Предлагается модификация закона упрочнения, рассмотренного выше [Д2], для учета влияния температуры и скорости деформации.
Для определения макронапряжений используется процедура осреднения Тейлора по представительному объему, включающему 400 зерен. Предлагаемая модель встроена в конечно-элементный пакет ABAQUS. Подробно описаны процедура и результаты идентификации модели, выполненная для чистого (99.987%) алюминия и алюминиевого сплава (ГЦК–решетка). Для идентификации использованы известные в литературе экспериментальные данные по одноосному растяжению образцов при нескольких значениях постоянных скоростей деформаций и температур. Полученные параметры были далее применены для теоретического предсказания поведения материала при одноосном нагружении со скачками по скорости деформаций и температуре; режимы изменения скоростей деформаций и температур выбраны аналогичными реализуемым в известных из литературы экспериментах. Сравнение расчетных и экспериментальных данных по зависимостям напряжение–деформация показывают хорошее соответствие.
В работе [Д26] приведено краткое описание эволюции микроструктуры при деформировании ГЦК-монокристаллов (ячейки, блоки ячеек, субзерна, дислокационные стенки, разделяющие ячейки и блоки). Для описания микроструктуры предлагается ввести внутренние переменные, моделирующие блоки ячеек и дислокационные стенки. В качестве основного ОС используется закон Гука, записанный для разгруженной конфигурации. Скорости сдвигов по СС определяются из закона Орована; скорость движения дислокаций устанавливается кинетическим законом, учитывающим энергию активации дислокаций, температуру, сдвиговые напряжения, плотности мобильных дислокаций и дислокаций леса. Основываясь на принципе максимума работы напряжений на пластических деформациях, получают выражение для плотности мобильных дислокаций. Представляется странным, что плотность мобильных дислокаций пропорциональна корню квадратному плотности дислокаций леса. На основе того же принципа для случая «композита» из блоков ячеек и стенок выведено выражение для плотности мобильных дислокаций как функции плотностей дислокаций в блоках ячеек и дислокационных стенках. Предложены основанные на рассмотрении дислокационных реакций кинетические уравнения для изменения плотностей иммобильных дислокаций в блоках ячеек и в дислокационных стенках.
Для моделирования «композита» из блоков и стенок для каждой системы скольжения предлагается использовать модель Максвелла, в которой в силу сложности реализации пренебрегается упругими составляющими сдвигов. В итоге построенная модель имеет в своем составе десять материальных констант. Авторы отмечают, что вследствие построения всех кинетических уравнений на основе теории дислокаций указанные константы имеют ясно выраженный физический смысл и, по крайней мере, известен порядок этих величин. Авторами проведен физический анализ и обоснованы интервалы возможных значений каждой из констант, входящих в модель. Разработанная модель использована для анализа сжатия монокристалла алюминия при трех скоростях нагруже-
312
ния (0.2, 2 и 20 н/с) и трех различных температурах (623, 673 и 723оК). Сопоставление теоретических результатов с экспериментальными показывает удовлетворительное соответствие. Отмечается, что в дальнейшем модель предполагается расширить на более широкий температурный диапазон и ОЦК-кристаллы и встроить её в конечноэлементную программу.
Впоследние годы для модификации различных физических теорий все чаще исследователи применяют модели обобщенных континуумов (градиентные теории – в особенности). Остановимся детально на одной из первых работ по данному направлению [Д13], основанной на концепции так называемых «геометрически необходимых дислокаций» (восходящей к работам [Д32, Д3, Д19]). Согласно этой концепции наряду со «статистически накопленными дислокациями» [Д3], являющимися следствием однородного пластического деформирования, вблизи областей неоднородности пластических сдвигов (например, в окрестности границ зерен) появляются дислокационные субструктуры типа стенок дислокаций, дислокационных ячеек и т.д., которые должны обеспечить совместность деформации решетки и обеспечить искривления–кручения решетки, которые и называются «геометрически необходимыми дислокациями».
Всоответствии с указанной концепцией авторы представляют поликристалл совокупностью двух «фаз» – примерно однородно деформируемых «ядра» зерен и бикристаллических зон, моделирующих участки границы каждого из зерен.
Вкачестве основы для описания поведения «зон однородности» принята упруговязкопластическая модель [Д18], основанная на мультипликативном разложении Ли, изотропном гиперупругом законе, в котором в качестве мер напряженного и деформированного состояния выбраны соответственно второй тензор Пиола–Кирхгоффа и тензор деформаций Коши–Грина, определенные в терминах промежуточной (разгруженной) конфигурации.
Основное отличие от известных моделей кристаллов заключается в упомянутой выше «двухфазности» материала. Поликристалл представляется совокупностью «ядер» зерен и приграничных областей – бикристаллов. При этом бикристаллические зоны подразделяются да две подобласти – «внутреннюю» и «внешнюю» (для каждого зерна), каждая из этих подобластей «наследует» ориентацию систем скольжения зерен, примыкающих к моделируемому участку границы. На границе подобластей задаются дополнительные условия совместности по градиентам места и напряжениям. Полные деформации в «ядре» зерен и осредненные деформации в каждом бикристалле полагаются равными осредненным деформациям (т.е. принята гипотеза Фойгта).
Напряжения в зерне определяются осреднением по объему «ядра» и бикристаллов, окружающих зерно (с учетом объемной доли «ядра» и бикристаллической границы). В представительном объеме напряжения определяются осреднением по совокупности зерен (сумма напряжений в зернах, деленная на число зерен, составляющих представительный объем).
Полагается, что «геометрически необходимые дислокации (ГНД)» накапливаются с ростом деформации во внутренней части бикристаллов, их плотность определяется разностью пластических составляющих градиентов места в ядре и внутренней части бикристаллов. Появление ГНД связывают с дополнительным (по отношению к увеличению критических напряжений за счет «статистически накопленных дислокаций») упрочнением систем скольжения. Предлагаемая модель использована для анализа одноосного растяжения образца с акцентом на проверку справедливости соотношения Холла–Петча. Результаты расчетов по предлагаемой модели сопоставлялись с теоретическими результатами прямого конечно-элементного моделирования и экспериментальными данными для поликристаллической меди со средним размером зерна 14, 33 и 220 мкм, показано их хорошее соответствие.
313
К данному направлению относится работа [Д27]. Отмечается, что основанные на однородности деформирования (сдвигом) мод е- ли и связанной с этим однородности распределения дислокаций в системах скольжения оказываются недостаточно адекватн ыми при описании поведения материала на более малых масштабах. Для описания локальных искажений (кривизн –кручений) кристаллической решетки требуется введение неоднородных дислокационных субструктур, которые авторы также относят к «геометрически н е- обходимым дислокациям». В связи с этим приведенная в [Д26] м о- дель модифицируется введением дополнительной внутренней п е- ременной – тензора плотности геометрически необходимых дисл о- каций (ГНД) и кинетического уравнения для неё, определяющее скорость изменения тензора ГНД через градиент скорости сдвигов. Последнее при использовании предлагаемой модели совместно с конечно-элементным пакетом требует вычисления в каждой гау с- совой точке интегрирования вычисления указанных градиентов, что существенно усложняет процедуру инт егрирования, в связи с чем значительная часть работы посвящена описанию предлагаем о- го авторами эффективного алгоритма интегрирования. Разработа н- ный алгоритм встроен в коммерческий конечно -элементный пакет MSC.Marc200x и использован для анализа деформирова ния простым сдвигом монокристаллического алюминиевого образца. С о- поставление результатов расчета (кривые сдвиговые напряжения – сдвиговые деформации, интенсивности деформаций на боковой поверхности образца, сдвиговая деформация – до 55%) с полученными авторами экспериментальными данными показывают хор о- шее соответствие. Для анализа влияния масштабного фактора пр о- ведены расчеты для образцов с уменьшенной высотой (1/2 и 1/10 от исходного), показано, что с уменьшением высоты образца п о- вышаются сдвиговые напряже ния и существенно изменяются поля плотности дислокаций и разориентаций решетки.
В статье [Д28], в которой получили развитие положения из рассмотренных выше работ, отмечается важность учета в моделях поликристаллов границ зерен, которые могут служить мощны м препятствием для мобильных дислокаций. Предполагается, что подвижные дислокации могут пересекать границу зерен, оставляя в ней дислокацию ориентационного несоответствия (ДОН), пар а- метры которой авторы предлагают определять из условия миним у- ма энергии ДОН. Для моделирования влияния границ предлагается использовать, как и для внутренности зерен, вязкопластическую модель с дополнительной энергией активации, пропорциональной энергии образования ДОН. Для численной реализации модели та к- же применяется конечно –элементный пакет MSC.Marc200x и специальные элементы для учета границ зерен.
314
Разработанная модель применена для анализа процесса д е- формирования бикристалла с ГЦК -решеткой (алюминий) для трех разориентировок (авторы называют их «малой», «средней» и «большой»). В проведенных экспериментах и численных расчетах (простой сдвиг до 50%) показано, что по мере увеличения разор и- ентировок возрастает неоднородность интенсивности деформаций в кристаллах, составляющих бикристалл, что обусловлено возра с- тающим сопротивлени ем движению дислокаций границы криста л- лов. Сопоставление результатов экспериментально измеренных на боковой поверхности образца интенсивностей деформаций и ор и- ентировок с данными расчетов показывает хорошее соответствие.
В статье [Д29] рассматривается модификация предложенной авторами модели [Д27, Д28] для описания поведения моно - и поликристаллов с ОЦКрешеткой. В отличие от ГЦК -кристаллов, где барьер Пайерлса мал по сравнению с сопротивлением дислокаций леса движению мобильных дислокаций, для ОЦК -кристаллов, напротив, можно пренебречь напряжениями от леса дислокаций в сравнении с напряжением Пайерлса; в остальном модель не отл и- чается от изложенной в цитируемых выше работах. Модифицир о- ванная модель использована для анализа деформирования бикр и- сталла ниобия при выдавливании образца через прямоугольную матрицу. Результаты расчетов сопоставляются с данными пров е- денных авторами экспериментов. Отмечается, что лучшее соотве т- ствие достигается при использовании для ОЦК -решетки в качестве потенциально активных с истем скольжения <111>, {110} и <111>, {112}.
Структурно–аналитическая теория
Значительный вклад в развитие физических теорий внесен р а- ботами В.А.Лихачева и В.Г.Малинина. Обобщающие результаты многолетней работы по созданию модели, названной авторами структурно-аналитической теорией прочности и пластичности, содержатся в монографии [48], где приведен также весьма о б- ширный список публикаций авторов.
Анализируя состояние физических тео рий пластичности, авторы отмечают, что основным концептуальным недостатком этих теорий являлось описание процессов деформирования, основанное на рассмотрении поведения самой малой части, которую можно выделить в материале (например, субзерно, фрагмент), н е- учет самоорганизованной многомасштабности процессов неупр у- гого деформирования и разрушения.
В основу теории авторами положены следующие положения: 
Для описания поведения материала используется дву х- уровневая модель (микро - и макроуровень), для каждого
315
из уровней вводится представительный объем; в пределах представительного объема соответствующие параметры каждого из уровней полагаются однородными.
Все микрообъемы взаимодействуют друг с другом через микронапряжения. При этом вводится дополнительное поле микронапряжений, разделенное на две составляющие
– ориентированные и неориентированные микронапряж е- ния. Поля ориентированных микронапряжений порожд а- ются неоднородными неупругими макродеформациями и не исчезают при снятии внешней нагрузки (в макросмы с- ле). Поля неориентированных микронапряжений обусло в- ливаются многими причинами, к числу которых относя т- ся: несовместности температурных деформаций микр о- объемов, неоднородности упругих характеристик на ми к- роуровне, неоднородностей магнитострикционных и электрострикционных микродеформаций, неоднородность неупругих микродеформаций.
Процессы деформирования на микро - и макроуровнях связаны между собой через соответствующие поля напр я- жений и деформаций.
Физические константы теории являются фундаментал ь- ными характеристиками материала и не зависят от способа их калибровки в макроэкспериментах (принцип л о- кальной калибровочной инвариантности).
В качестве процедуры осреднения принимается ориентационное и статистическое осреднение (по некоторым параметрам).
Детально анализируется большинство из известных механи з- мов упругого и неупругого деформирования (температурные, ма г- нитострикционные, электрострикционные, диффузионные, вязкие (деформации ползучести), сдвиговые, деформации двойникования, деформации за счет мартенситных реакций). Для каждого из указанных механизмов записываются определяющие напряжения ми к- роуровня, связывающие скорости микродеформаций со скоростями и полными эффективными микронапряжениями. Для тензора ск о- рости микродеформаций принимается гипотеза об аддитивности скоростей микродеформаций по всем реализующимся механизмам.
Учитывая тот факт, что основными механизмами неупругого деформирования моно - и поликристаллических металлов являются кристаллографический сдвиг и двойникование, рассмотрение этих механизмов выделено в отдельную главу. Приведены соотношения конститутивной модели для описания пластического деформир о- вания, деформаций ползучести (с разделением их на деформации
316
ползучести, обусловленные возвратом, и деформации термоакт и- вируемой ползучести). Приведены рез ультаты численных расчетов для различных пропорциональных и сложных нагружений, отмеч а- ется их хорошее качественное соответствие экспериментальным данным. Значительная часть монографии посвящена анализу про ч- ности и разрушения поликристаллов, а также рассмот рению деформирования материалов с мартенситным механизмом неупруг о- го деформирования (в частности , материалов, обладающих эффектом памяти формы). Указанные вопросы выходят за рамки тематики предлагаемой работы.
Задачи и упражнения
1)Длинный цилиндрический тонкостенный трубчатый образец с
первоначальными размерами l0 , a0 , d0 (d0 a0 l0 ) находится под
действием некоторой нагрузки (рис. 1), из-за чего испытывает деформацию, в результате которой приобретает размеры l, a, d (d a l ) , d d0 , кроме
того, торцы оказываются повернутыми относительно друг друга (вокруг оси образца) на угол .
l |
a |
|
F
M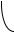 
d
Рис. 1. Тонкостенный трубчатый образец под нагрузкой
Можно считать, что во всех точках образца, достаточно удаленных от торцов, компоненты тензоров деформации в цилиндрической СК одинаковы. Определить физические компоненты следующих тензоров деформации:
а) тензора деформации Коши–Грина, б) тензора деформации Альманси, в) тензора малых деформаций, г) левого тензора деформации Генки, д) правого тензора деформации Генки.
317
2) |
1)Длинный тонкостенный трубчатый образец находится в равновесии |
|||||||||
под действием следующих сил (рис. 1): на каждом торце приложена |
||||||||||
растягивающая вдоль оси сила M F и крутящий относительно оси образца |
||||||||||
момент M, кроме того, известна разность внутреннего и внешнего давлений |
||||||||||
p=p2 -p1 . |
|
|
|
|
|
|
|
|
|
|
|
Можно считать, что во всех точках образца, достаточно удаленных от |
|||||||||
торцов, компоненты тензоров напряжений в цилиндрической СК одинаковы. |
||||||||||
Считая все размеры образца в каждый момент деформирования известными, |
||||||||||
по измеряемым силе, давлению и моменту определить физические |
||||||||||
компоненты для тензора напряжений Коши и тензоров напряжений Пиола– |
||||||||||
Кирхгофа. |
|
|
|
|
|
|
|
|
|
|
3) |
1) Какими должны быть величины F, M, p для трубчатого образца (см. |
|||||||||
упр. 1.2), чтобы нетривиальной была только следующая компонента тензора |
||||||||||
напряжений: |
|
|
|
|
|
|
|
|
||
|
а) |
zz |
(реализуется «чистое растяжение»); |
|
||||||
|
б) |
z |
(реализуется «чистый сдвиг»). |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
4) Пусть в результате испытания образца получены следующие |
||||||||||
зависимости для величин, приведенных на рис.1 (см. упр.1,2): F(t ) , M(t ), |
||||||||||
p(t) , |
l(t ), |
(t ) (при этом толщина d |
d(t ) определяется из условия упругой |
|||||||
сжимаемости): |
|
|
|
|
|
|
|
|||
|
l |
|
|
|
|
a |
|
|
|
k |
|
l * |
|
|
|
|
|
|
|
* |
|
|
|
kl |
|
|
|
|
2 |
|||
|
|
|
|
|
|
|
||||
|
|
|
2 |
a * |
|
ka2 |
|
|||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
kl |
|
|
|
|
ka |
|
|
k |
|
|
1 |
|
|
|
|
1 |
|
|
1 |
|
O t * |
|
t O t * |
|
t O t * |
t |
|||||
|
F |
|
|
|
|
M |
|
|
p |
|
|
|
|
|
|
|
|
|
|
p * |
kp |
|
F * |
|
kF |
|
|
|
|
kM |
|
2 |
|
|
|
|
M * |
|
2 |
|
|||
|
|
|
2 |
|
|
|
|
|
||
|
kF |
|
|
|
kM |
1 |
|
kp |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
O t * |
|
t O t * |
|
t O t * |
t |
|||||
|
|
|
|
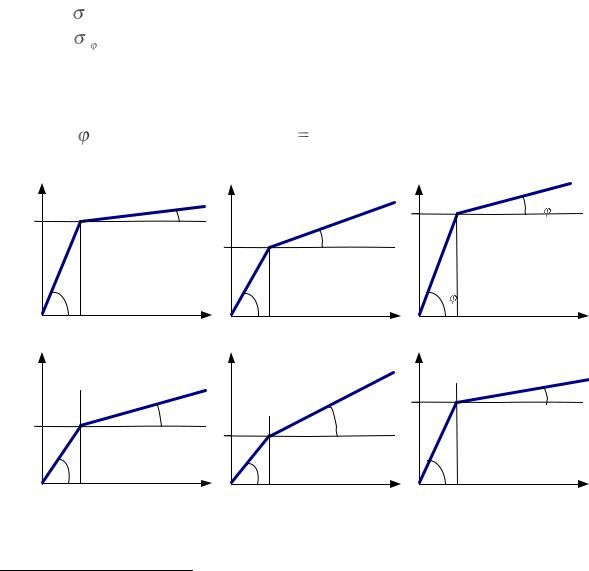
Рис.2. Идеализированные опытные данные |
|
|||||
1) Механика сплошных сред в задачах. Т.1. Теория и задачи./ под ред. М.Э. Эглит. М.:
Московский лицей. 1996. 396 стр.
318
а) |
зависимость |
F(t ) , |
l(t ) |
согласно |
рис. |
2, |
остальные |
величины |
нулевые; |
|
|
|
|
|
|
|
|
б) |
зависимость |
M(t ), |
(t ) |
согласно |
рис. |
2, |
остальные |
величины |
нулевые; |
|
|
|
|
|
|
|
|
в) |
зависимость |
p (t ), |
a(t ) |
согласно |
рис. |
2, |
остальные |
величины |
нулевые; |
|
|
|
|
|
|
|
|
г) все зависимости согласно рис. 2. |
|
|
|
|
||||
Построить кривые σ |
ε |
при использовании различных мер |
||||||
деформации и энергетически сопряженных с ними мер напряжений для приведенных экспериментальных данных (численные значения параметров задаются самостоятельно).
5)Предложите и обоснуйте процедуру идентификации соотношения (3.1); постройте зависимость потенциала от межатомного расстояния для различных значений показателей степени.
6)Доказать, что не существует оси симметрии 5-го порядка.
7)Построить сферические проекции зеркальных плоскостей симметрии и осей симметрии для кристалла кубической системы.
8)Показать, что индексы любой плоскости могут быть определены как сумма индексов двух плоскостей, лежащих по разные стороны от рассматриваемой, сферические проекции которых расположены на одной дуге большого круга (рис. 3.10).
9)Построить стереографические проекции зеркальных плоскостей симметрии и осей симметрии для кристалла кубической системы.
10)Показать, что для кристаллов кубической системы достаточно рассмотреть только один из 24 треугольников на стереографической проекции.
11)Построить схематичный рисунок винтовой дислокации, обозначить линию дислокации, ввести контур Бюргерса и указать вектор Бюргерса.
12)Рассмотреть систему из трех пластин одинаковой толщины, находящихся в естественном состоянии, контакт считать идеальным, упругие
характеристики всех пластин одинаковы. При незначительном изменении температуры средняя пластина испытывает твердотельное фазовое превращение, при котором её удельный объем возрастает на 3 %.
319
Качественно определите напряженное состояние пластин. Как оно изменится, если удельный объем при фазовом превращении уменьшится?
13)Для условий предыдущей задачи определить качественное распределение напряжений при вторичном (обратном) фазовом переходе в случаях: а) первичный фазовый переход приводит только к упругим деформациям всех пластин; б) первичный фазовый переход приводит к появлению пластических деформаций только в средней пластине; в) первичный фазовый переход приводит к появлению пластических деформаций только в крайних пластинах; г) первичный фазовый переход приводит к появлению пластических деформаций во всех трех пластинах.
14)На схематичном рисунке кристаллической решетки обозначить плоскости и направления скольжения краевых дислокаций для ГЦКкристалла и ОЦК-кристалла.
15)Дополнить рис. 3.13 (тетраэдр Томпсона) указанием направлений и плоскостей сдвига.
16)Рассмотреть дислокационную реакцию в ГЦК-кристалле: расщепление частичной дислокации на две дислокации Шокли.
17)Рассмотреть дислокационную реакцию в ГЦК-кристалле: объединение дислокации Франка и дислокации Шокли.
18)Рассмотреть дислокационную реакцию в ГЦК-кристалле: объединение единичной дислокации и дислокации Шокли из разных плоскостей скольжения.
19)Рассмотреть образование барьера Ломера–Коттрелла в ГЦК-кристалле.
20)Рассмотреть дислокационную реакцию в ОЦК-кристалле: объединение n полных дислокаций в n-кратную дислокацию и обратную реакцию.
21)Рассмотреть все возможные реакции расщепления полной краевой дислокации в ОЦК-кристалле.
22)Рассмотреть реакцию расщепления винтовой дислокации в ОЦК– кристалле.
320