Теория определяющих соотношений. Часть 2. Теория пластичности

10.Дайте формулировку постулата изотропии в частной форме. В чем состоит его значимость для построения ОС?

11.Приведите формулировки гипотезы локальной определенности, поясните её значение для формулировки конкретных соотношений теории пластичности.

12.Сформулируйте гипотезу компланарности, поясните её значение для построения конкретного вида ОС.

13.В чем преимущества формулировки гипотезы компланарности в виде (5.16) по сравнению с (5.13)?

14.Запишите соотношение теории малых упругопластических деформаций, укажите область её применимости.

15.Сформулируйте соотношение теории малой кривизны, определите область её применимости.

16.Запишите варианты соотношений теории средней кривизны, предложенные В.И. Малым.

17.В чем основные отличия от предшествующих вариантов соотношений, предложенных С.В. Ермаковым и Дао Зуй Биком?

18.Запишите соотношения теории пластичности для двухзвенных ломаных в приращениях.

19.Приведите соотношения теории двухзвенных ломаных в терминах векторов напряжений и деформаций.

20.Запишите ОС в истокообразной форме, предложенные А.А. Ильюшиным, сопоставьте их с соотношениями теории средней кривизны.

Теория необратимых процессов, несмотря на сосуществование в ней большого количества вариантов, отнюдь не является наукой противоречивой или нелогичной. Все эти варианты укладываются в стройную систему и представляют собой своего рода приборы, отличающиеся друг от друга разрешающими способностями.

В.В. Новожилов, Ю.И. Кадашевич

6. Некоторые модификации теории пластического теч е- ния

Изучаемая в университетских курсах МДТТ классическая теория пластического течения (ТПТ) базируется на понятии поверхности текучести, ассоциированном законе течения и трех основных законах упрочнения (изотропного, кинематического и комбинированного типов) (см. гл.4). В теориях, использующих неассоциированный закон течения, наряду с поверхностью текучести вводится так называемый пластический потенциал (или диссипативная функция) (см. гл. 4). Из многочисленных экспериментальных данных известно, что ТПТ позволяет описывать процессы деформирования с достаточной для прикладных задач МДТТ точностью лишь при нагружениях, близких к простым (деформирование по траекториям малой кривизны, см.

201

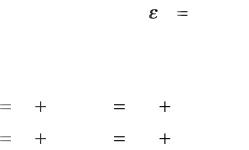
гл.5). Данное обстоятельство, имеющее широкое экспериментальное подтверждение, стимулировало исследования в теории пластического течения, имеющие целью создание теории, позволяющей описывать процессы сложного нагружения без отказа от основных положений теории течения.

Созданные и создаваемые в последние десятилетия в рамках ТПТ теории

сконцентрированы на построении различных законов упрочнения. При построении законов упрочнения различают одноповерхностные и многоповерхностные теории [55, 64], в рамках каждой из которых формулируются законы трансляции (переноса без изменения формы) и эволюции формы поверхности (поверхностей) течения. Собственно определяющие соотношения ТПТ в дальнейшем получают, как правило, с использованием принципа градиентальности, согласно которому бесконечно малое приращение тензора (девиатора) пластических деформаций пропорционально градиенту (в пространстве девиаторов напряжений) функции, описывающей поверхность текучести (в случае ассоциированного закона течения), или пластического потенциала (в случае неассоциированного закона течения). Иными словами, вектор бесконечно малых приращений пластической деформации направлен по нормали к соответствующей поверхности текучести в текущей точке процесса нагружения. Здесь будут рассматриваться получившие большее распространение ОС ТПТ, основанные на ассоциированном законе течения. Вероятно, основной причиной широкой популярности указанных соотношений является достаточно простой и прозрачный формализм формулировки ОС, ясное физическое обоснование основных понятий теории.

При построении модификаций ТПТ обычно сохраняются и другие гипотезы классической ТПТ. В частности, принимается линейная связь первых инвариантов тензоров напряжений и деформаций (средних напряжений и деформаций), аналогичные приведенным в гл.5. Пластические деформации обычно полагаются изохорическими, I1 ( p ) 0. В рамках геометрически ли-

нейных теорий принимается гипотеза об аддитивном разложении тензора

(девиатора) полных деформаций на упругую и пластическую составляющие:

Следует отметить, что для случая больших градиентов перемещений следует использовать введенное Ли мультипликативное разложение градиента места [57]. Приемлемым является также аддитивное разложение тензора деформации скорости на упругую и пластическую составляющие, D=De + Dp, ведущее, однако, к появлению неголономных мер деформации.

Для упругих составляющих тензора деформаций в большинстве теорий полагается справедливым закон Гука. Таким образом, в дальнейшем можно сосредоточить внимание на рассмотрении соотношений для девиаторов напряжений и пластических деформаций.

202

Одноповерхностные теории течения

Рассмотрим одноповерхностные теории течения. Для определенности будем применять критерий текучести Мизеса, модифицированный введением так называемого тензора остаточных микронапряжений ρ (или «обратных

напряжений» по зарубежной терминологии, «back stress» (англ.)) [28, 29]. Уравнение поверхности текучести в этом случае имеет вид

где s – параметр, характеризующий длину дуги (пластической) деформации,

Очевидно, что соотношение (6.2) представляет собой математическую запись комбинированного закона упрочнения. Отметим, что если в качестве R(s) используется сопротивление деформации σT (s) , определяемое в опытах на од-

ноосное нагружение, то перед первым членом в выражении функции текучести (6.2) следует поставить множитель 3/2.

Хотя в математическую структуру ОС теории пластического течения тензор ρ впервые был введен А.Ю. Ишлинским [21], его название и физиче-

ское толкование было дано несколько позднее в работах Ю.И. Кадашевича и В.В. Новожилова [28, 29, 55]. Механизм пластического течения рассматривался по аналогии с сухим трением. Отправной точкой в рассуждениях является известный экспериментальный факт (см. гл.3) о «запасаемой» в ходе пластического деформирования материалом энергии, которая и связывается авторами с упругими микродеформациями и микронапряжениями. В качестве основной причины возникновения остаточных микронапряжений полагалась несовместность пластических сдвигов в соседствующих зернах поликристаллического агрегата (так называемый стесненный сдвиг), в силу чего при нагружении возникают упругие взаимодействия зерна с окружением. После разгрузки эти упругие деформации и соответствующие им напряжения сохраняются в зернах, уравновешиваясь силами сухого трения. При повторном нагружении в первоначальном направлении для достижения пластического деформирования необходимо вначале преодолеть накопленные упругие внутризеренные напряжения (остаточные микронапряжения), что и создает, по мнению авторов, эффект «кажущегося возрастания сил сухого трения». При реверсивном же нагружении вслед за разгрузкой остаточные напряжения, напротив, способствуют началу пластического деформирования, т.е. порождают «кажущееся снижение сил сухого трения».

Вероятно, с позиций ФТТ ситуация может показаться чрезмерно упрощенной (см. гл.3), однако качественно, как представляется, суть явления уловлена с удивительной (для времени появления теории) прозорливостью и прозрачностью. Именно поэтому указанная теория и её модификации в течение уже многих десятилетий являются одними из самых распространенных в теории пластичности.

203

Остаточные микронапряжения присущи не только поликристаллам, но и монокристаллическим материалам (по крайней мере – при сколь-нибудь развитых (более 10%) пластических деформациях), где их возникновение обусловлено формированием дислокационных субструктур и их взаимодействием с дислокациями и другими дефектами (см. гл. 3). Из сказанного следует, что тензор ρ представляет собой явную внутреннюю переменную (см. Вве-

дение) наряду с радиусом поверхности текучести R(s), также являющимся явной внутренней переменной, характеризующей микроструктуру материала. Несколько забегая вперед, отметим, что замыкание конститутивных соотношений здесь осуществляется на макроуровне, ρ и R(s) определяются через

макроскопические пластические деформации (аналогичным образом замыкаются, например, соотношения теории турбулентности Рейнольдса).

С использованием принципа градиентальности основное соотношение теории течения для комбинированного закона упрочнения может быть записано в виде

Простейшим вариантом этого соотношения является предложенное еще в 1929 г. А. Рейссом уравнение теории течения, следующее из (6.3) в предположении ρ =0 и R=const.

Следует отметить, что здесь в рассмотрение не включены теории с поверхностями текучести, испытывающими искажения формы (что в действительности имеет место, см. гл. 2), в силу их редкого использования в практике; последнее обусловлено прежде всего математическими и экспериментальными трудностями, возникающими при применении подобных теорий. В рассматриваемых теориях поверхность текучести может испытывать однородное расширение (сжатие) без искажения формы.

Основное различие в разрабатываемых модификациях ТПТ состоит в применении разных законов движения центра поверхности течения, положение которого определяется тензором ρ . Большинство из известных (замы-

кающих) уравнений для ρ представляют собой тензорно-линейные связи ме-

жду тензором остаточных микронапряжений и девиатором пластических деформаций и их производными. При этом простыми алгебраическими операциями можно получить ОС, связывающие девиатор напряжений и его первую производную с девиатором пластических деформаций, первой и второй производной последнего, что оправдывает отнесение ОС вида (6.3) к тензор- но-линейным соотношениям второго порядка [55] (ниже этот вопрос рассмотрен более подробно). В первых теориях данного типа (А.Ю. Ишлинский (1954), Ю.И. Кадашевич и В.В. Новожилов (1957)) предложены достаточно простые эволюционные уравнения; обширная сводка соотношений для ρ со-

держится в работах В.В. Новожилова, Ю.И. Кадашевича и их сотрудников [30, 55 и др.]. Для классификации этих соотношений запишем уравнение для

204

описания эволюции тензора остаточных микронапряжений в достаточно общем (для рассматриваемых теорий) виде

где a, b, c, g – материальные функции или константы, определяемые экспе-

риментально (вообще говоря, в опытах на сложное нагружение).

Если продифференцировать ОС (6.3) по s, затем из полученного соот-

щему виду тензорно-линейных определяющих соотношений второго порядка

[22]:

где α0 ,α1,β0 ,β1,β2 – материальные функции, определяемые в макроскопиче-

ских опытах [3]. Заметим во избежание недоразумений, что несмотря на присутствие в (6.5) вторых производных от девиатора пластических деформаций (по длине дуги пластической деформации!) данные ОС относятся к классу простых определяющих соотношений (или материалов первого порядка) [61, 62]. Наличие данного члена указывает на зависимость отклика материала не только от проекции приращения пластической деформации на касательную к траектории деформации, но и от проекции на нормаль. В этом смысле ОС (6.5) примыкает к соотношениям теории УПП А.А. Ильюшина.

В приведенной ниже табл. 6.1 содержится сводка о наиболее известных уравнениях, описывающих эволюцию тензора остаточных микронапряжений в процессе пластического деформирования ρ [55].

Таблица 6.1 Конкретизация уравнения для тензора остаточных микронапряжений (6.4)

Приведенный перечень не претендует на полноту и завершенность, соотношения одноповерхностной теории течения продолжают появляться и модифицироваться. Напомним, что здесь не рассматриваются теории с изменяющейся формой поверхности текучести, хотя работы в этом направлении также ведутся.

Несколько особняком стоит предложенное Д. Бакхаузом в 1972 г. соотношение

где b, L – материальные функции. Нетрудно видеть, что в уравнение Д. Бакхауза (6.6) явным образом введена память о предшествующей истории деформации; появляется дополнительная возможность учета памяти за счет введения ядра L(s s ') , характеризующего затухающую память. Конечно, к

виду (6.6) могут быть приведены и различные варианты, следующие из (6.4), однако вопрос о затухающей памяти потребует наложения некоторых ограничений на материальные функции, отсутствовавших в исходной форме ОС.

Несмотря на различия в виде соотношений для описания эволюции центра поверхности текучести, все они основаны на анализе результатов макроэкспериментов и определенных эвристических соображениях.

Более детально с приведенными теориями интересующийся читатель может ознакомиться в монографии [55]. Дальнейшее развитие теории пластичности в рамках тензорно-линейных определяющих соотношений второго порядка нашло отражение в монографии В.С. Бондаря [3]. В цитируемой работе, в частности, рассматриваются ОС теории пластичности для материалов, чувствительных к виду напряженного состояния, материалов, испытывающих дополнительное циклическое упрочнение, а также теории пластичности для описания процессов неизотермического нагружения и при наличии ионизирующих воздействий. Отличительной особенностью монографии, выгодно отличающей её от многих других, является детальное описание процедур идентификации всех рассмотренных моделей.

206

Многоповерхностные теории течения

В конце 60-х годов появилась серия работ, посвященных созданию так называемых многоповерхностных теорий течения. Создание их было в первую очередь обусловлено неудовлетворительным описанием существующими в то время одноповерхностными теориями эффекта Баушингера и процессов циклического деформирования (в особенности – при сложном нагружении). Остановимся более подробно на теории, предложенной в пионерской работе З. Мруза [74].

Рассмотрим вначале случай одноосного нагружения, диаграмма которого представлена на рис. 6.1. Материал полагается начально изотропным. При растяжении материал на начальной стадии испытывает упругие деформации (участок OF0 , рис 6.1), модуль упругости равен E0 E . После достижения

помощью n линейных сегментов с постоянными модулями E1, E2 ,...,En (заметим, что текущее значение касательного модуля определяется как d / d ),

). Вопрос о приемлемой аппроксимации решается исследователем. Для определенности будем полагать, что при аппроксимации одинаковы длины участ-

няется модуль пластичности Ck 1 Ck (т.е. сопротивление пластическому деформированию), который сохраняется вплоть до достижения напряжения

k.

Предположим теперь, что после достижения конца этапа m (на рис. 6.1 m=3) начинается разгрузка и нагружение в обратном направлении. На участке FmR0 (рис. 6.1) нагружение осуществляется упругим образом, причем про-

тяженность участка FmR0 вдвое превышает протяженность соответствующего участка OF0 первоначального активного нагружения.Обоснование этому

можно найти в физическом рассмотрении упругопластических деформаций. Если принять, что упругие деформации обеспечиваются искажениями кристаллической решетки, то после искажения в одном направлении кристаллическая решетка может испытать двойное искажение в обратном направлении без необратимых деформаций. На участке R0 R1 деформирование осуществ-

ляется неупругим образом, модуль пластичности равен модулю C1 соответствующего участка F0 F1 , протяженность участка R0 R1 также вдвое превыша-

207

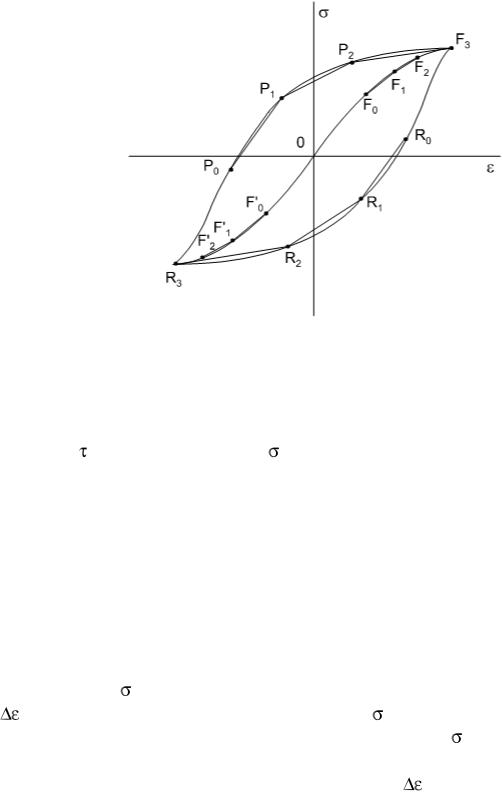
ет протяженность участка F0 F1 первичного нагружения.

Рис.6.1. Схема к модели З.Мруза (одноосное нагружение)

Для объяснения этого факта можно принять следующий механизм. Участку Fk -1Fk с модулем пластичности Ck отвечает определенный набор кри-

сталлографических плоскостей и направлений скольжения с критическим напряжением k–1, соответствующим k–1. Вероятно, можно предположить, что повышение напряжения обусловлено упрочнением, связанным с остановкой дислокаций на различных препятствиях, прекращением действия дислокационных источников. При обратном нагружении на первой стадии необратимые деформации обусловливаются движением и аннигиляцией уже накопленных на препятствиях дислокаций; на второй стадии источники начинают действовать в обратном направлении (по существу, повторяется – с точностью до направления – картина первичного нагружения).

Для описания данного механизма пластического деформирования можно предложить следующую структурно-механическую (имитационную) схему. Введем пластический элемент с ограничениями, характеризуемый напряжением активации a , модулем пластичности C и предельными деформациями p . До достижения в элементе напряжения a он ведет себя как жесткое тело; после того, как напряжение достигает напряжения a , элемент деформируется с сопротивлением пластической деформации C вплоть до реализа-

вновь становится жестким.

Тогда структурно-механическая модель рассматриваемой теории З.Мруза может быть представлена в виде последовательности упругого элемента и совокупности n пластических элементов с ограничениями (рис 6.2). Следует отметить, что если модули упрочнения Ck полагаются постоянны-

208

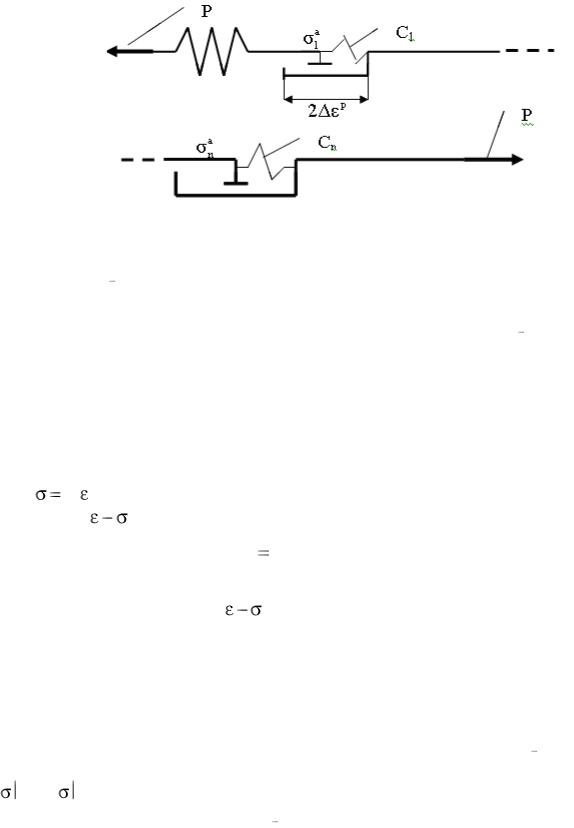
ми, то напряжения активации σak зависят от предыстории пластических де-

формаций всех элементов. Приведенная модель достаточно хорошо иллюстрирует одноосное нагружение.

Рис. 6.2. Структурно-механическая модель к теории Мруза

Аналогичным образом описывается нагружение на последующих участках R1R2...Rm 1Rm . Нетрудно видеть, что напряжения в точках Rm и Fm равны

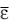
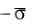по модулю и противоположны по знаку. Начиная с точки Rm кривая обратного нагружения FmR0R1...RmRm+1... совпадает с кривой OF0'...Fm 1'Rm..., получаемой из кривой прямого нагружения центральносимметричным отражением относительно точки O. Отметим, что при описании реверсивного нагружения обычно вводят повернутую на 180систему координат c началом координат в точке начала разгрузки. Нетрудно видеть, что кривая обратного нагружения FmR0...Rm... однозначно определяется кривой прямого нагружения OF0...Fm... Действительно, если задана кри-

падает с соотношением, полученным Г.Мазингом (1927) при рассмотрении одноосной модели, состоящей из совокупности параллельно соединенных упругих и идеально пластических элементов с различными (распределенными по стохастическому закону) пределами текучести.

Если в точке Rm вновь осуществляется изменение направления нагружения, то нагружение будет осуществляться по кривой RmP0P1...Pm 1Fm и далее по кривой начального нагружения. При циклически изменяющихся между Fm и Rm напряжениях деформирование будет происходить по установив-

шемуся циклу FmR0R1...RmP0P1...Pm 1Fm .

Перейдем теперь к рассмотрению общего случая. В пространстве напряжений каждому значению напряжений σ0 ,σ1,...,σn ставятся в соответст-

209

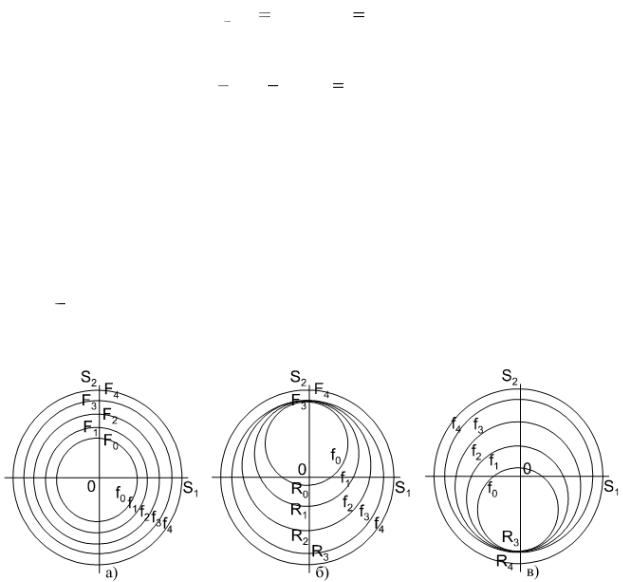
вие гиперповерхности f0 ,f1,...,fn ; в случае условия Мизеса в пространстве девиаторов напряжений эти гиперповерхности представляют собой гиперсферы. Поверхность f0 отделяет область упругого поведения материала от

области упругопластических деформаций; в исходном положении начало координат (в пространстве напряжений) содержится внутри области, ограниченной поверхностью f0 . Поверхности f1 ,...,fn определяют области постоян-

ных модулей пластичности; в исходном положении поверхности fk содержат внутри себя поверхности fk l (k 1, 2,..., n;l 1, 2,..k) , нигде не пересекаются

и не касаются. Уравнения поверхностей имеют одинаковый вид; например, для k-й поверхности справедливо уравнение

где σ(0k ) – постоянная (напряжение течения (сопротивление деформации), со-

ответствующее концу k-го участка), q – постоянная, ρ(k ) – девиатор остаточ-

ных микронапряжений, определяющий положение k-й гиперповерхности. Полагается, что функция f(.) является однородной степени q; следовательно, описываемые этими функциями поверхности являются подобными, в начальном положении – концентрическими. В дальнейшем для простоты иллюстрации будем в основном пользоваться двумерным случаем. При использовании условия Мизеса гиперповерхности f0 ,f1,...,fn в пространстве девиато-

ров S1 S2 будут представлять в начальном положении семейство концен-

трических окружностей (рис. 6.3, а)).

Рассмотрим вначале простое циклическое нагружение вдоль оси S2 .

Рис.6.3. Иллюстрация к модели Мруза (случай одноосного нагружения в двумерном пространстве напряжений)

В рассматриваемой модели предполагается, что каждая из гиперпо-

верхностей может перемещаться только поступательно (трансляционные перемещения) без изменения своей формы.

На начальной стадии нагружения изображающая точка в пространстве напряжений (ИТН) движется от точки О вдоль оси S2 до достижения предела

текучести в точке F0 , деформирование на участке OF0 осуществляется упру-

210