
Теория определяющих соотношений. Часть 2. Теория пластичности
.pdf
1. Поликристалл представляет собой агрегат из большого числа хаотично ориентированных зерен.
2. Поведение каждого из зерен описывается жесткопла стической моделью; деформации зерен осуществляются только криста л- лографическим сдвигом по известным для данного материала кр и- сталлографическим системам (скольжения).
3. Упрочнение одинаково во всех плоскостях скольжения и определяются свойствами монокриста лла.
4. Границы зерен имеют нулевую толщину, не осуществляют вклада в механизмы неупругого деформирования.
5. Деформации (или деформации скорости) полагаются одн о- родными в пределах макроскопического представительного объема (гипотеза Фойгта), т.е. p ( k ) = < p > = (или Dp ( k ) = <Dp >= D). Кроме
того, поскольку деформации осуществляются |
сдвигом, в этом |
случае отсутствует изменение объема, т.е. p ( k ) |
= ep ( k ) = <ep > = |
(или Dp ( k ) = dp ( k ) = <dp >= d). |
|
В наиболее распространенных кристаллах с ГЦК и ОЦК р е- шеткой число систем скольжения существенно превышает число независимых компонент девиатора деформаций (см. гл. 3), что обусловливает неоднозначность определения сдвигов по криста л- лографическим плоскостям по заданному девиатору деформаций. Указанное обстоятельство является одной из существенных трудностей построения физических теорий пластичности. Как избежать этой трудности?
Для ее преодоления Тейлором был предложен эвристический принцип, суть которого состоит в следующем. Полагается, что любая деформация (или приращение деформации) осуществляется сдвигом не более чем по пяти независимым системам скольжения,
определенным из условия минимальности суммарного сдвига .
Представляющий , по существу, гипотезу, данный принцип минимума сдвига основывался на наблюдениях за поведением одино ч-
ных кристаллов. |
|
Обозначим через dγ(k ) |
приращение сдвига в n-м зерне по k-й |
(n) |
|
системе скольжения (соответствующая скорость сдвига обознач а- ется как γ((kn)) ). Тогда принцип минимума сдвига математически з а- писывается в виде
Kn |
|
|
|
|
γ(k ) |
min |
n = 1, N , (8.7) |
||
(n) |
|
|
|
|
k =1
при этом в силу принятой гипотезы Фойгта должно выполняться ограничение
251
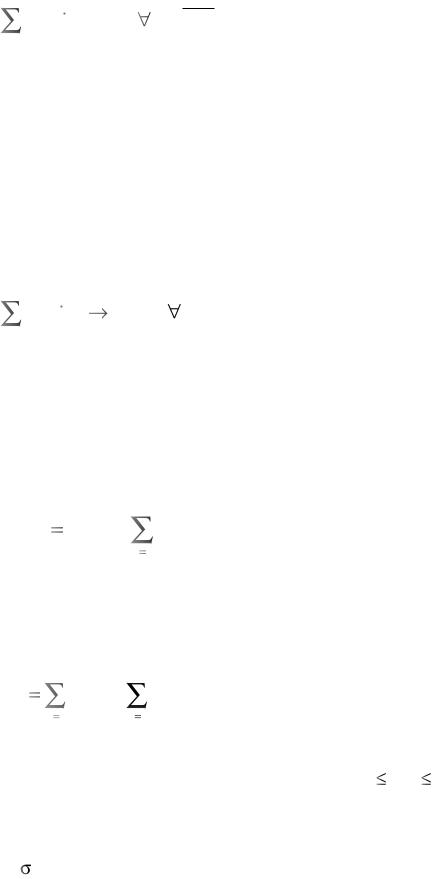
Kn
M((kn)) γ((kn)) = d n = 1, N , (8.8)
k =1
где d – предписанный (заданный в каждый момент деформиров а- ния) девиатор деформации скорости; здесь в обозначении орие н- тационного тензора появился индекс п, относящийся к номеру зерна; в дальнейшем он будет сохраняться только в случае, если из контекста не ясно, что ориентационный тензор относится к сист е- мам скольжения определенного зерна. Заметим, что в случае отк а- за от предположения об изотропном упрочнении в каждом из зерен принцип минимума сдвига трансформируется в принцип минимума мощности, согласно которому действительные скорости сдвига доставляют минимум мощности (по сравнению с кинематически возможными скоростями сдвигов):
Kn |
|
|
|
|
τ(n)k γ(k ) |
min |
n = 1, N . (8.9) |
||
c (n) |
|
|
|
|
k =1 |
|
|
|
|
Более подробно принцип минимума мощности рассмотрен ниже.
Как отмечено выше, критические напряжения сдвига в исхо д- ной модели Тейлора приняты одинаковыми во всех системах да н-
ного зерна и обозначаются как . Тогда элементарная работа
dA( п ) , произведенная в п-м зерне объемом V( п ) , определяется соотношением:
|
|
Kn |
dA n |
V n τcn |
dγkn , (8.10) |
|
|
k 1 |
где Кn – число активных систем скольжения в данном п-м зерне в рассматриваемый момент нагружения.
Элементарная работа dA, производимая на сдвигах по акти в- ным системам скольжения в агрегате из N монокристаллов, определяется следующим соотношением:
N |
|
Kn |
|
dA |
V n τcn |
dγkn . |
(8.11) |
n 1 |
|
k 1 |
|
Заметим, что в правой части (8.11) суммирование по числу активных систем скольжения осуществляется от 1 до Кn , т.е. в различных зернах это число может быть различным (1 Кn 5).
В модели Тейлора полагается, что вся подводимая к образцу
механическая энергия расходуется на совершение пластич е-
ской деформации. В случае одноосного нагружения (при действии напряжения 1 1 ) элементарная работа внешних сил в предполож е- нии одноосного макроскопического напряженн о- деформированного состояния равна
252

σ11dε11( V (n) ) σ11dε11p ( V (n) ) .
Тогда, приравнивая работу внешних напряжений и работу внутренних сдвиговых напряжений, получаем:
N |
N |
|
Kn |
|
σ dε ( |
V (n) ) |
(V (n) (n) |
dγ(n) ) . |
(8.12) |
11 11 |
|
C |
k |
|
n 1 |
n 1 |
|
k 1 |
|
Предполагая, что все зерна имеют одинаковый объем, око н- чательно получаем:
1
σ11dε11 N
N |
Kn |
|
τcn |
dγkn |
(8.13) |
n 1 |
k 1 |
|
Последнее соотношение позволяет построить кривую одноо с- ного нагружения поликристалла с использованием модели мон о- кристалла. Процедура пошагового пос троения кривой состоит в следующем.
Пусть кривая построена для определенной предшествующей деформации 1 1 , т.е. известны напряжения 1 1 во все предшествующие моменты нагружения, накопленные сдвиги, критические напряжения сдвига во всех зернах; ориентация з ерен полагается неизменной и известной.
|
Задается достаточно малое приращение деформации |
1 1 , яв- |
|||||
ляющееся |
одновременно |
приращением главной |
деформации |
||||
1 |
=Δ |
1 1 |
; из условия несжимаемости два других главных значения |
||||
приращений деформаций |
2 =Δ 3 = –1/2Δ 1 (при этом |
2 =Δ 2 2 , |
|||||
3 |
=Δ |
3 3 |
, |
все остальные |
компоненты тензора |
равны |
нулю). |
Следует подчеркнуть, что в данном случае главные оси тензоров 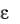 и
и 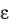 совпадают и неизменны. По заданному тензору
совпадают и неизменны. По заданному тензору 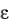 данного шага нагружения в каждом зерне определяются приращен ия сдвигов по активным системам скольжения, обеспечивающие мин и- мальность приращения суммарного сдвига.
данного шага нагружения в каждом зерне определяются приращен ия сдвигов по активным системам скольжения, обеспечивающие мин и- мальность приращения суммарного сдвига.
По накопленным сдвигам (с учетом приращений на рассма т- риваемом шаге) определяются критические напряжения сдвига в
каждом зерне τcn , n 1, N , после чего легко опреде ляется значе-
ние правой части (8.13) и величина 1 1 .
Тейлор применил описанную процедуру для построения кр и- вой одноосного деформирования алюминия (ГЦК -решетка). Результаты расчета хорошо согласуются с экспериментальными да н- ными, что подтверждает приемлемость модели для рассмотрения, по крайней мере, одноосного нагружения.
Таким образом, модель Тейлора [84] сводится к минимизации мощности работы на сдвигах (в пространстве скор остей сдвигов) (8.9) при ограничении (8.8), после чего для определения девиатора
253

напряжений используется (8.3) (или (8.4)) с ориентационными тензорами, соответствующими активным системам скольжения.
Постановку задачи минимизации мощности для каждого зе р- на можно переформулировать следующим образом. Введем об о- значения (определив компоненты тензоров в базисе ЛСК):
c = {τ1 |
, τ2 |
,..., τ5}T , |
|
|
. . |
|
. |
}T , |
|
|
|||
x = {γ , γ |
,..., γ |
|
|
||||||||||
c |
|
|
c |
|
c |
|
|
1 2 |
|
5 |
|
|
|
A = [A |
ij |
], A |
= M1 |
|
,A |
= M2 |
,...,A |
= M5 |
, |
||||
|
|
|
11 |
11 |
12 |
11 |
|
15 |
11 |
|
|||
...................................................
A51 = M131,A52 = M312 ,...,A55 = M315 ,
b = {bi}, b1 = d11, b2 = d22 , b3 = d12 , b4 = d23, b5 = d31.
Тогда задачу (8.9)–(8.8) можно записать в канонической фо р- ме задачи линейного программирования:
min cT x, Ax=b,
(А)
x 0.
Процедура решения следующая: из решения возможных для данного типа кристаллов систем линейных алгебраических ура в- нений (А2 ) (каждая из систем содержит в общем случае 5 уравнений) определяются соответствующие наборы скоростей сдвигов; из них сразу «отбраковываются» решения, содержащие отриц а- тельные компоненты вектора х. Из оставшихся «наборов» опред е- ляется удовлетворяющий (А1 ).
Заметим, что в с обственно модели Тейлора девиатор напр я- жений вообще отсутствует, напряжения априори полагаются так и- ми, что активизируют все необходимые для реализации предп и- санной скорости деформации системы скольжения, причем число СС равно числу независимых компонент де виатора напряжений. Компоненты девиатора напряжений определяются на втором этапе, после определения активных система скольжения и скоростей сдвига по ним. Для этого используется закон Шмида, предста в- ляющий в этом случае систему линейных алгебраических урав нений относительно компонент девиатора напряжений (число ура в- нений равно числу активных систем скольжения).
Резюмируя, можно отметить следующие проблемы, возн и- кающие при применении модели Тейлора .
Неединственность определения совокупности 5 скоростей сдвига, реализующих предписанный девиатор скоростей деформ а- ций.
Возможное несоответствие напряженного состояния виду деформированного состояния (например, при одноосном деформ и- ровании напряженное состояние может отличаться от одноосного).
254
Невозможность определения тензора напряжений по ско-
ростям девиатора деформаций, поскольку имеем материал со св я- зью (несжимаемость).
Не исключена ситуация, когда минимум мощности достигае т- ся на совокупности систем скольжения с числом нетривиальных скоростей сдвига, меньшем 5 (например, при совпадении систем скольжения с плоскостями и направлениями главных скоростей сдвига). Эта ситуация соответствует нахождению изображающей точки в пространстве напряжений (ИТН) на грани или ребре мн о- гогранника текучести. Ряд авторов трактует данную ситуацию как так называемое вырождение системы уравнений. Это представл я- ется не совсем верным. Действительно, в модели Тейлора поиск осуществляется именно в вершинах многогранника и число ура в- нений должно соответствовать числу неизвестных компонент девиатора напряжений (случай большего числа упомянут выше). О д- нако в данном случае (8.9) не дает критерия отбора единственного набора активных систем скольжения (нулевые с двиги), и решению с точки зрения минимума мощности сдвига удовлетворяют все ИТН в вершинах многогранника текучести, примыкающие к да н- ной грани или ребру, хотя напряжения при этом существенно о т- личаются. Последнее возможно, например, в случае чистого сдв и- га при такой «благоприятной» ориентации одной из систем скол ь- жения, что предписанная деформация (сдвиг) реализуется за счет сдвига только по данной системе скольжения.
Невыполнение условий равновесия на границах зерен.
Сложность реализации модели , связанная с необходимо-
стью определения активных систем скольжения и сдвигов в них, доставляющих минимум суммарному сдвигу. Процедура решения данной задачи минимизации оказывается весьма трудоемкой.
Неучет в модели Тейлора упругих деформаций.
Достаточно грубым является также предположение об одн о- родности деформаций в зернах, что не соответствует результатам микроэкспериментов, особенно в случае сложного нагружения. В реальных процессах деформирования микродеформации неодн о- родны даже в пределах каждого зерна и субз ерна.
Заметим, что часть (п. 2, 3, 4) из указанных выше недоста т- ков в известных авторам работах не отмечалась. Однако и отм е- ченных ранее оказалось вполне достаточно, чтобы стимулировать исследователей к совершенствованию модели Тейлора. В первую очередь появились работы, направленные на «подведение» под модель Тейлора более глубокой математической «базы», замена интуитивно высказанных положений математически строго док а- занными. При этом основные положения и гипотезы модели Те й- лора остались неизменными. К числу наиболее ярких работ этого
255

направления относятся статьи Бишопа и Хилла [67, 68], подробно анализируемые ниже.
Модель Бишопа–Хилла
В модели используются некоторые положения макроскопич е- ской теории пластичности . Для полноты изложения ниже напоминаются ее основные понятия и положения. В частности, использ у- ется понятие поверхности текучести, f(S)= s ; принимаются соот-
ношения ассоциированного закона течения, dep dλ Sf . Полагает-
ся, что упругими деформациями можно пренебречь; пластическое деформирование осуществляется без изменения объема, d p =dep .
В теории используется также введенный в макроскопической теории пластичности принцип максимума работы (см. гл. 4). Пусть в некоторый момент нагружения действительное напряже н- ное состояние в рассматриваемой частице определяется тензором и отвечает состоянию пластического (упругопластического) д е- формирования (т.е. изображает положение на поверхности тек у- чести). Данному состоянию отвеча ет тензор приращения деформаций d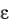 (d
(d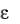 = d p = dep ), направленный согласно сказанному выше
= d p = dep ), направленный согласно сказанному выше
по нормали к поверхности текучести. Далее, пусть |
* |
– напря- |
|
жение, не нарушающее условие текучести при данном положении и размерах поверхности текучести, т.е. * отвечает точка в пространстве напряжений, лежащая внутри или на поверхности тек у- чести. В силу выпуклости последней угол между ( – *) и направлением внешней нормали к поверхности текучести (а следовател ь- но – d ) должен быть острым, откуда
( – |
*):d |
0, d 0. |
(8.14) |
В последнем соотношении знак равенства возможен только в |
|||
случае, если |
и * |
отличаются гидростатическим давлением. Со- |
|
отношение (8.14) представляет собой математическую формул и- ровку принципа максимальной работы (гл.4): из всех возможных
напряжений (т.е. не нарушающих условие текучести) действ и- тельное напряжение производит максимальную работу на пр и- ращении (пластических) деформаций .
Предполагая, что тензоры напряжений и * удовлетворяют однородному уравнению равновесия, учитывая, что (8.14) выполняются для произвольной точки тела, нетрудно получить следу ю- щее соотношение:
(T T* ) du dS 0 , (8.15)
S
256

где T, T* – соответствующие , * поверхностные нагрузки. Заметим, что соотношения (8.14), (8.15) не зависят от наличия или отсутствия упрочнения и анизотропии материи.
В цитируемых работах Бишопа и Хилла доказывается также обратное (в определенном смысле) утверждение: если для зада н- ного d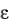 напряжения доставляют стационарное (или максимал ь- ное) значение работе по сравнению со всеми близкими напряж е- ниями *, не выходящими за пределы поверхности текучести, т о существует пластический потенциал, и он совпадает с поверхн о- стью текучести; в случае максимальности работы соответству ю- щая поверхность (изопотенциальная или поверхность текучести) является строго выпуклой.
напряжения доставляют стационарное (или максимал ь- ное) значение работе по сравнению со всеми близкими напряж е- ниями *, не выходящими за пределы поверхности текучести, т о существует пластический потенциал, и он совпадает с поверхн о- стью текучести; в случае максимальности работы соответству ю- щая поверхность (изопотенциальная или поверхность текучести) является строго выпуклой.
Для полноты изложения модели Бишопа –Хилла остановимся на всех этапах ее построения, начиная с монокристалла, хотя часть положений не отличается от рассмотренных выше.
Пластичность монокристалла
Полагается, что пластическое деформирование осуществляе т- ся только сдвигом по известным кристаллографическим с истемам; ориентационные тензоры последних, как и ранее, будут обозн а- чаться как M( k ) , k=1,...,К. Соответствующий бесконечно малым
приращениям микросдвигов d ( k ) (скоростям микросдвигов )
тензор (девиатор) микродеформаций de (de = dep = d ) (девиатор деформации скорости d) определяется линейной комбинацией
микросдвигов по кристаллографическим системам: dε |
M k |
dγ k |
|||
|
|
|
|
k |
|
( d |
M k |
γ k ), причем тензор |
(или d) имеет пять независимых |
||
|
k |
|
|
|
|
компонент.
Авторы сохраняют здесь используемую в цитируемых раб о- тах Бишопа и Хилла терминологию, относящуюся к уровню зерен (микросдвиги, микродеформации и т.д.). В современной литерат у- ре параметры, относящиеся к уровню зерен и субзерен, трактуются как величины мезоскопического уровня (мезоуровня).
Очевидно, что тензор d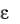 однозначно определяется по заданным d ( k ) . Однако обратное неверно, причем возможны различные ситуации. Если число возможных систем скольжения (СС) К<5, в случае произвольной деформации отсутствует комбинация сдв и- гов, реализующая d . Отметим, что в данном случае невозмож на реализация произвольной деформации только за счет скольжения краевых дислокаций и в рассмотрение необходимо вводить другие моды деформации, например движение винтовых дислокаций, п е- реползание краевых дислокаций, движение точечных дефектов. В
однозначно определяется по заданным d ( k ) . Однако обратное неверно, причем возможны различные ситуации. Если число возможных систем скольжения (СС) К<5, в случае произвольной деформации отсутствует комбинация сдв и- гов, реализующая d . Отметим, что в данном случае невозмож на реализация произвольной деформации только за счет скольжения краевых дислокаций и в рассмотрение необходимо вводить другие моды деформации, например движение винтовых дислокаций, п е- реползание краевых дислокаций, движение точечных дефектов. В
257
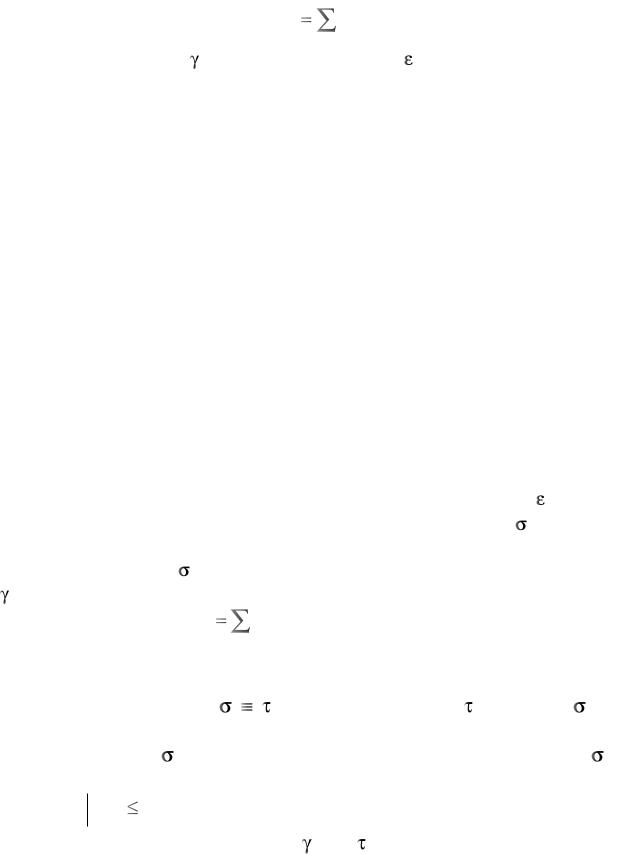
случае К=5, при условии линейной независимости ориентационных
тензоров M( k ) , |
в разложении dε |
M k |
dγ k |
существует |
единст- |
||
|
|
|
k |
|
|
|
|
венное решение для d |
( k ) , определяемых по d . |
|
|
|
|||
В случае, |
когда |
К>5, могут |
быть |
определены |
C5 |
наборов |
|
|
|
|
|
|
|
K |
|
сдвигов, реализующих данную деформацию, однако следует и с- пользовать только множества линейно независимых сдвигов. В общем случае могут быть найдены множества шести и более сдв и- гов по кристаллографическим системам, производящих заданную деформацию (понятно, что в их числе линейно независимых может быть не более пяти). Отметим, что из чисто кинематических (ге о- метрических) соображений установить единственную совоку п- ность сдвигов не удается, и это представляет одну из сложностей физических теорий.
В модели Бишопа–Хилла обычно принимается, что упрочн е- ние одинаково в активных и неактивных системах скольжения; о д- нако при этом в активных системах возможно различие критич е- ских напряжений по противоположным направлениям скольжения, т.е. условие текучести имеет вид (8.4). В оригинальном варианте модели [67] законы упрочнения практически не обсуждаются, п о- скольку не приводят к изменению структуры теории и ее основных соотношений.
Для монокристалла также формулируется и доказывается
принцип максимальности (максимума) работы. Пусть d – при-
ращение деформации, реализующееся в монокристалле, – тензор напряжений, вызывающий эту деформацию. Пусть имеется другой
тензор напряжений |
*, |
не нарушающий |
условие текучести. Через |
|
d ( k ) обозначим элементарные сдвиги |
по активным системам |
|||
скольжения, так что |
dε |
M k |
dγ k , причем суммирование в пра- |
|
|
|
k |
|
|
вой части ведется только по номерам активных систем скольж е- ния. На активных системах скольжения должно выполняться усл о-
вие текучести, т.е. M( k ) : |
( k ) = |
τ(k ) . Обозначим * ( k ) |
=M( k ) : * – |
|
|
c |
|
сдвиговое напряжение в k-ой системе скольжения, соответствующее напряжению * . В силу предположения о допустимости * (т.е. ненарушении условия текучести) имеем
τ* k |
τck . (8.16) |
Отметим также, что знаки d ( k ) и ( k ) в данном случае всегда одинаковы и положительны (каждое из направлений в плоскости скольжения образует собственную систему скольжения). Тогда н е- трудно установить следующее соотношение:
258

dA - dA σ : dε σ* : dε σ σ* : dε |
τck |
τ* k |
dγ k |
0, |
||||
откуда |
|
|
|
|
|
|
|
|
dA σ : dε |
τck |
dγ k |
τ k |
dγ k |
σ* : dε |
dA* . (8.17) |
||
Соотношение (8.17) представляет собой математическую з а-
пись принципа максимальной работы для монокристалла .
Отметим, что в физических теориях часто используются п о- нятия геометрически и физически возможных систем сдвигов, или,
при векторном представлении |
в Rn , соответствующих векторов |
||
сдвига. |
Вектор сдвига называется геометрически возможным , |
||
если он |
реализует предписанную пластическую |
деформацию ep |
|
(аналогично – для приращений d |
и dep ). Вектор d |
называется фи- |
|
зически возможным, если он реализуем для данного напряженного состояния, т.е. в соответствующих системах скольжения выпо л- няется условие текучести.
Для определения физически и геометрически возможных ве к- торов сдвига d в теории Бишопа–Хилла используется упомянутый выше принцип минимума сдвига. Пусть d – задаваемое приращение деформаций, – тензор напряжений, инициирующий эту д е-
формацию активизацией сдвига d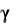 и удовлетворяющий условию текучести. Предположим, что d * – вектор сдвига, также эквивалентный d (т.е. геометрически возможный), однако не обязател ь- но вызываемый некоторым напряжением, удовлетворяющим усл о- вию текучести (т.е. не являющийся физически возможным). Зам е-
и удовлетворяющий условию текучести. Предположим, что d * – вектор сдвига, также эквивалентный d (т.е. геометрически возможный), однако не обязател ь- но вызываемый некоторым напряжением, удовлетворяющим усл о- вию текучести (т.е. не являющийся физически возможным). Зам е-
тим, что |
в силу выполнения условия текучести для т ензора |
ком- |
поненты |
( k ) вектора сдвиговых напряжений в любой k-й системе |
|
скольжения не превосходят критического напряжения сдвига |
τ(k ) . |
|
|
|
c |
Для геометрически и физически возможного вектора d в К активных системах скольжения ( k ) = τ(ck ) , в остальных d ( l ) =0. При этом
в активных системах скольжения знаки d ( k ) и ( k ) совпадают и положительны. Для геометрически (но не физически) возможного
вектора d * в |
каждой системе скольжения | ( k ) | |
τ(k ) , при этом |
||||||||||
|
|
|
|
|
|
|
|
|
|
c |
||
знаки d ( k ) и |
( k ) |
могут быть произвольными (т.е. |
( k ) может быть |
|||||||||
как положительным, так и отрицательным). |
|
|
|
|||||||||
С учетом сказанного выше получаем |
|
|
|
|||||||||
σ : dε τ dγ |
τ k dγ k |
τ k dγ* k , |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
τ k dγ k |
|
τck |
dγ k |
, |
τ k dγ* k |
τ k |
|
dγ* k |
|
τck |
dγ* k |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно,
259

τck |
dγ k |
τck |
dγ* k |
. (8.18) |
Последнее соотношение представляет собой принцип минимума сдвига Тейлора, расширенный на случай неоднородного упрочнения ; иногда его называют принципом минимума р аботы. Полагая, что упрочнение одинаково во всех системах скольжения, из (8.18) получаем
dγ k |
|
dγ* k |
, (8.19) |
представляющее собой математическую запись принципа минимума сдвига Тейлора : сумма абсолютных значений прир а- щений физически и геометрически возможных сдвигов не прево с- ходит суммы абсолютных значений приращений геометрически возможных сдвигов. Из доказательства следует также, что если существует более одной системы физически и геометрически во з- можных сдвигов, то сумма абсолютных значений приращений сдвигов во всех таких систе мах будет одинаковой.
Остановимся на соответствии двух сформулированных выше принципов, один из них – принцип максимума работы, второй – принцип минимума работы. Даже названия принципов, поставле н- ные рядом, могут вызвать некоторое недоумение; действительно , в обоих принципах речь идет об одной и той же величине – элементарной работе, но первый постулирует для этой величины макс и- мум, а второй – минимум. Не являются ли такие утверждения взаимоисключающими?
Ответ на поставленный вопрос отрицательный. При форм у- лировке экстремальных принципов (более широко – вариационных принципов) важно различать параметры, которые являются зада н- ными, неизменными (возможно – только в некоторый момент рассматриваемого процесса), и параметры, которые можно изменять, перебирать, варьировать. В зависимости от этого величина, эк с- тремальность которой устанавливается, может принимать макс и- мальное или минимальное значение (а может не обладать экстр е- мальными свойствами, в каждом конкретном случае последние н а- до устанавливать).
Аналогичным образом дело обстоит и с рассматриваемыми принципами. В первом из них – принципе максимума работы – варьируемой величиной является тензор напряжений, а бесконечно малое приращение деформаций является величиной заданной, н е- изменной в данный момент процесс а. Во втором принципе ситуация «зеркально отражается»: тензор напряжений считается зада н- ным, а варьируемыми параметрами являются бесконечно малые приращения сдвигов. Такие принципы в математической физике и
260
