
Теория определяющих соотношений. Часть 2. Теория пластичности
.pdf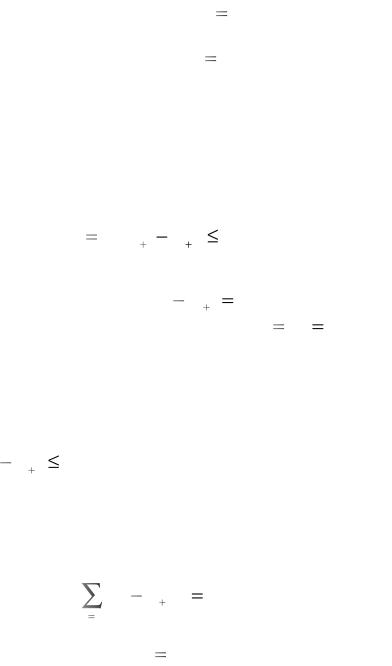
его девиатора). Полагается, что деформирование осуществляется упругим образом до тех пор, пока изображающая точка в пространстве напряжений не достигнет некоторой характерной для данного материала поверхности – поверхности пластичности (или поверхности текучести). В шестимерном пространстве напряжений поверхность пластичности может в некоторых направлениях простираться до бесконечности, в девиаторном пространстве напряжений поверхность пластичности всегда замкнута.
Для начально изотропного материала поверхность пластичности должна быть функцией инвариантов тензора напряжений Коши. При этом, как уже отмечалось, для металлов и сплавов в широком диапазоне изменения среднего напряжения последнее практически не оказывает влияния на возникновение пластического деформирования, о чем свидетельствуют многочисленные экспериментальные исследования [2]. При использовании данного предположения для начально изотропного материала условие пластичности (текучести) может быть записано в виде
f (I2 (S), I3 (S);σs ) 0, |
(4.15) |
или
f (S1,S2 ,S3 ;σs ) 0, |
(4.16) |
где Si – главные значения девиатора напряжений S , I2 (S), I3 (S) – второй и третий ин-
варианты S . Отметим, что вводимый критерий пластичности должен выполняться и для случая одноосного растяжения–сжатия или для случая чистого сдвига.
Одним из исторически первых были критерий Треска–Сен-Венана, называемый также условием постоянства максимальных касательных напряжений. Согласно этому критерию наступление пластического деформирования отвечает достижению на одной из площадок максимальных касательных напряжений характерной для данного материала величины
| τi | |
1 |
| σi 1 |
σi 2 | |
1 |
σs , |
(4.17) |
|
2 |
2 |
||||||
|
|
|
|
|
где σs – предел текучести материала (определяется в опытах на одноосное нагружение), индексы взяты по модулю 3. Соотношения | σi σi 1 | σs представляются в пространстве напряжений правильной шестигранной призмой с осью σ1 σ2 σ3 , равнонаклонен-
ной к осям главных напряжений (вдоль этой оси призма простирается в бесконечность); след этой поверхности на девиаторной плоскости представляет собой правильный шестиугольник. НДС, определяемое изображающими точками внутри призмы, является упругим; наступлению пластического деформирования соответствует выполнение одного или двух условий (4.17) со знаком равенства, т.е. положению изображающей точки на одной из граней или ребре призмы. Заметим, что (4.17) может быть записано в терминах девиа-
тора напряжений: | Si Si 1 | σs .
Недостатком критерия Треска–Сен-Венана является наличие особых точек (ребер) поверхности текучести, что создает определенные трудности при дальнейшем применении его для построения определяющих соотношений. В связи с этим, Мизесом (а позднее Губером и Генки) было предложено заменить шестигранную призму описанным круговым цилиндром
3 |
|
|
|
|
|
(S |
S |
|
)2 |
2σ2 |
(4.18) |
i |
i 1 |
|
s |
|
|
i 1 |
|
|
|
|
|
или |
|
|
|
|
|
|
σu |
σs |
|
(4.19) |
|
или |
|
|
|
|
|
150

τи |
1 |
|
σs . |
(4.20) |
|||||
|
|
|
|||||||
3 |
|||||||||
|
|
|
|
|
|
|
|||
В некоторых случаях вводят предел текучести при чистом сдвиге τs |
1 |
|
σs и послед- |
||||||
|
|
|
|||||||
3 |
|||||||||
|
|
|
|
|
|
|
|||
нее условие записывается в виде τи τs .
Эксперименты показывают достаточную для практических расчетов точность рассмотренных критериев текучести. При этом для поликристаллических материалов условие текучести Мизеса (называемое иногда условием Мизеса–Губера–Генки) выполняется несколько лучше, чем условие Треска–Сен-Венана.
Следует отметить, что исключение из критерия пластичности первого инварианта тензора напряжений является достаточно обоснованным для так называемых компактных материалов. В то же время для пористых сред, порошковых материалов среднее напряжение существенно сказывается на наступлении и протекании процесса пластического деформирования. В связи со сказанным в критерий текучести и определяющие соотношения по-
добных материалов входит и первый инвариант I1 (σ) .
Заметим также, что, по существу, в критерии пластичности, описанные выше, входит лишь второй инвариант тензора напряжений. Отсутствие в нем третьего инварианта объясняется геометрическим смыслом последнего (как направления сдвигового напряжения на октаэдрической площадке) и изотропностью материала. Однако подобное объяснение
едва ли можно признать удовлетворительным. Необходимость введения I3 (S) в условие
пластичности периодически обсуждается в публикациях по теории пластичности.
В процессе нагружения поверхность, разделяющая области упругого и пластического деформирования, называемая поверхностью нагружения, может претерпевать существенные
изменения положения и формы в пространстве напряжений Σ 5 (пятимерное девиаторное или соответствующее ему векторное пространство, см. гл.5). В случае, если поверхность пластичности неизменна, материал называют идеально–пластическим, а поверхность пластичности в этом случае называют поверхностью текучести [14]. Если же процесс пластического деформирования сопровождается изменением поверхности пластичности, то материал называется упрочняющимся; поверхность пластичности в этом случае иногда называют также поверхностью нагружения или поверхностью упрочнения. В дальнейшем, чтобы не создавать терминологические трудности, термины «поверхность пластичности» и «поверхность текучести» будут использоваться как синонимы, случай идеальной пластичности полагается частным случаем пластичности упрочняющихся материалов. Претерпеваемые поверхностью нагружения трансформации зависят от истории нагружения. С достаточной для многих технологических задач теории пластичности точностью претерпеваемые поверхностью нагружения изменения описываются с помощью двух распространенных законов упрочнения – изотропного и кинематического, или их комбинацией.
Закон изотропного упрочнения может быть записан в следующем виде: |
|
σu σT (q) , |
(4.21) |
где q – параметр, характеризующий предшествующую пластическую деформацию, σT
– сопротивление деформации («текущий предел текучести»). В качестве параметра q
может быть принята либо интенсивность пластических деформаций εup , либо накопленная
пластическая деформация sp (длина дуги пластической деформации). Аналогом последней является параметр Одквиста
151

q dHp |
2dep : dep . |
(4.22) |
В ряде работ в качестве данного параметра используется работа пластической деформации
q |
: d p . |
(4.23) |
Определение зависимости σT (q) осуществляется на основе экспериментальных данных с привлечением гипотезы единой кривой. Напомним, что согласно этой гипотезе интенсив-
ность напряжений зависит от интенсивности накопленных пластических деформаций sp (или от интенсивности пластических деформаций, или от некоторой иной величины, выбранной в качестве параметра q ), но не от вида НДС. В связи с этой гипотезой для опре-
деления σT (q) достаточно провести эксперименты по одноосному нагружению. Гипоте-
за единой кривой оказывается достаточно точной для углеродистых и низколегированных сталей, титановых сплавов; в то же время для некоторых алюминиевых и магниевых сплавов, для высокопрочных сталей имеют место отклонения от неё [59]. В качестве законов
изотропного упрочнения часто используются степенные функции вида |
σ |
Aqm B . |
|
T |
|
Кинематическое упрочнение описывает перемещение поверхности нагружения в пространстве напряжений, чем и обусловлено название. Один из наиболее распространенных законов кинематического упрочнения может быть представлен следующим соотношением:
3 |
(S ) : (S ) σ2 |
0 , |
(4.24) |
|
|||
2 |
s |
|
|
|
|
|
где – тензор (девиатор) так называемых «остаточных микронапряжений» (или «об-
ратных напряжений», back – stress), определяющий в данном случае положение центра гиперсферы в пространстве напряжений; в качестве эволюционного уравнения для мо-
жет использоваться, например, соотношение (предложенное независимо А.Ю. Ишлинским и В. Прагером) вида
d k dep , (4.25)
k – экспериментально измеряемая константа. Подробнее законы кинематического упрочнения будут рассмотрены при анализе модификаций теории пластического течения
(гл.6).
С помощью закона кинематического упрочнения можно описать хорошо известный в пластичности эффект Баушингера. Последний состоит в уменьшении предела текучести после разгрузки и нагружении «в обратном» по отношению к первоначальному направлению
деформирования в Э(5) .
Совместное использование законов (4.21) и (4.24) приводит к так называемому комбинированному закону упрочнения
3 |
(S ) : (S ) σ2 (q) 0 |
(4.26) |
2 |
T |
|
В общем виде условие пластичности тогда можно записать следующим образом:
f (S,ρ,q) 0 |
(4.27) |
или |
|
f (σ,ρ,q) 0 . |
(4.28) |
152

Отметим, что в случае неизотермического нагружения напряжение течения σT зависит также от температуры σT σT (q,θ) .
Большинство конструкционных материалов обладают свойством деформационного упрочнения. Однако в ряде случаев, особенно при повышенных температурах, деформационным упрочнением можно пренебречь и положить коэффициент деформационного уп-
рочнения |
E |
|
|
σT |
равным нулю. В этом случае материал называется идеально пласти- |
t |
|
|
|||
|
|
|
sp |
||
|
|
|
|
||
ческим, напряжение течения σT полагается постоянным и равным пределу текучести: |
|||||
σT (q) |
σs |
|
const . |
||
Понятно, что эволюция поверхности текучести при деформировании является следствием процессов изменения микроструктуры на мезо- и микроуровнях (вообще говоря, и на более низких масштабных уровнях). В связи с этим очевидно, что параметры, описывающие положение и форму этой поверхности с полным основанием можно отнести к (явным) внутренним переменным. Следует подчеркнуть, что построение адекватных исследуемому процессу пластического деформирования и достаточно универсальных законов, описывающих эволюцию поверхности текучести, требует тщательного рассмотрения физики процесса.
Формулировка определяющих соотношений классической теории пластичности базируется либо на одном из постулатов пластичности, либо на одном из принципов максимума, которые изложены ниже.
Постулаты пластичности
При построении определяющих соотношений теории пл а- стичности (впрочем, как и любой другой) важным моментом явл я- ется отделение ф изически реализуемых реализуемых от физически нереальных ситуаций при описании деформирования рассматр и- ваемых тел и формулировка соответствующих критериев. Указа н- ные критерии в макрофеноменологической теории пластичности являются обычно обобщением большого числа экспериментальных исследований, обоснованными с физической точки зрения, и фо р- мулируются в виде некоторых постулатов или принципов.
Одним из наиболее употребимых в теории пластичности является постулат Драккера: В любом замкнутом по напряжениям процессе нагружения (с началом в точке 
) работа дополнительных напряжений |
|
неотрицательна, т.е. |
|
|
A |
d 0 . |
(4.29) |
Представим входящие в подынтегральное выражение тензоры в виде |
|||
S σE (S S0 ) (σ σ E, d |
de dεE . |
||
Тогда |
|
|
|
A |
S : de |
3 σdε . |
|
|
S |
σ |
|
Поскольку в силу принятой ранее гипотезы dε |
dσ / K , второй член в правой части по- |
||
следнего соотношения может быть проинтегрирован: |
|
||
153
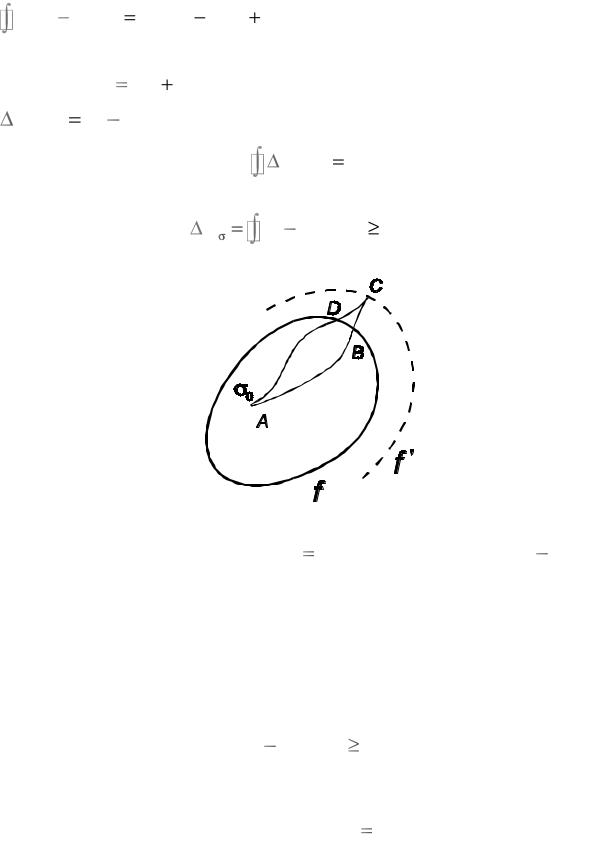
3 |
|
|
|
|
3 |
|
|
σ2 |
|
|
|
|
|
|||
|
|
(σ |
σ0 )dσ |
|
|
|
( |
|
|
σσ0 ) |
C , а так как интеграл определяется по замкнутому |
|||||
σ K |
|
|
K |
2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
контуру, то он равен нулю. Представив далее de |
суммой упругих и пластических со- |
|||||||||||||||
ставляющих, de |
dee |
|
|
dep , и производя аналогичные преобразования для члена |
||||||||||||
S : dee |
(S |
S |
|
) : |
dS |
, получаем |
|
|
|
|
||||||
0 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
2G |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
S : dee |
0 . |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
Тогда окончательно имеем |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
A |
(S S |
0 |
) : dep 0 . |
(4.30) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S
Рис. 4.2. Иллюстрация к постулату Драккера |
|
|
Знак равенства реализуется только при dep 0 или при ортогональности (S S |
0 |
) и |
|
|
dep . С учетом (4.30) получаем, что при чисто упругом деформировании (4.29) выполняется со знаком равенства, вклад в работу напряжений вносят только участки пластического деформирования. Рассмотрим деформирование по замкнутой по напряжениям траектории АВСDА (рис. 4.2), причем такое, что на участках AB и CDA деформирование осуществляется упругим образом (упругая нагрузка и упругая разгрузка), а участку BC отвечают
бесконечно малые приращения девиатора пластической деформации dep и бесконечно
малые изменения девиатора напряжений S . Тогда, пренебрегая малыми второго порядка, из (4.30) получаем
(S S |
) : dep |
0. |
(4.31) |
0 |
|
|
|
Последнее неравенство в теории пластичности иногда называют локальным принципом максимума. Отметим, что знак равенства в (4.31) при ненулевых пластических деформациях реализуем только для случая идеально-пластической среды; для упрочняющегося
материала знак равенства возможен только при dep 0.
Следует заметить, что физически реализуемым является выбор начальной точки S0
внутри или на поверхности текучести для любого анализируемого замкнутого цикла нагружения.
Неравенство (4.31) может быть представлено в векторной форме
154

(Σ Σ |
) : dэp |
0, |
(4.32) |
0 |
|
|
|
Рис. 4.3. Схема к постулату пластичности
т.е. угол между векторами добавочных напряжений (Σ Σ0 ) и приращений пластиче-
ских деформаций dэp всегда не тупой (рис.4.3). Отсюда следует, во-первых, что в совме-
щенных векторных пространствах деформаций Э(5) и напряжений Σ (5) вектор dэp направлен вне поверхности текучести по нормали к ней (в противном случае выбором Σ и Σ0 всегда можно добиться отрицательности рассматриваемого скалярного произведе-
ния); во-вторых, поверхность текучести должна представлять собой выпуклую (точнее – не вогнутую) поверхность (на рис. 4.3 изображена ситуация с нарушением последнего условия). Введенные выше условия текучести удовлетворяют второму положению; первое же используется при формулировке определяющих соотношений. При этом оно часто постулируется независимо в виде принципа градиентальности (или закона нормальности).
Следует отметить, что сам Драккер подчеркивал, что сформулированный им постулат не следует из термодинамики и называл его «квазитермодинамическим» [59].
Наряду с постулатом Драккера в теории пластичности широкое распространение имеет альтернативный постулат пластичности, сформулированный А.А. Ильюшиным:
Во всяком замкнутом по деформациям изотермическом процессе нагружения (деформирования) работа напряжений неотрицательна
A |
d |
0. |
(4.33) |
Аналогично приведенному выше можно показать, что |
|
||
A |
S : de |
Σ : dэ 0 . |
(4.34) |
Из постулата пластичности Ильюшина также следует принцип градиентальности. При этом можно показать, что A A , т.е. из (4.33) следует (4.29), но не наоборот.
Отметим, что в ряде работ по теории пластичности в силу связи векторов напряжений и деформаций условие текучести, принцип градиентальности и т.д. переформулируются в терминах пространства деформаций.
Альтернативные подходы к формулировке ОС теории пластичности основаны на использовании одного из принципов максимума.
155

Принципы максимума
Пластические деформации, как известно, являются необратимыми, работа напряжений на пластических деформациях почти полностью превращается в тепловую энергию (диссипирует). Мощность диссипации механической энергии (часто называемая также функцией диссипации) определяется соотношением
N p = σ : Dp . |
(4.35) |
Пусть Dp – некоторая предписанная скорость пластической деформации, σ – вызывающий эту скорость деформации тензор напряжений (можно назвать эти напряжения ассо-
циированными с Dp ); очевидно, что σ удовлетворяет (4.28). Введем тензор напряжений
σ , также удовлетворяющий условию пластичности (4.28), но не ассоциированный с Dp ; такие напряжения будем называть допустимыми. Тогда можно сформулировать следующий принцип максимума диссипации механической энергии:
При фиксированных параметрах ρ, q для предписанной скорости пластической де-
формации Dp из всех допустимых тензоров напряжений действительное напряжение σ , ассоциированное с Dp , производит максимальную мощность диссипации,
σ : Dp > σ : Dp . |
(4.36) |
Влитературе сформулированное утверждение называют иногда принципом максимума Мазинга [14]. Из принципа максимума, равно как из постулатов пластичности, вытекает выпуклость поверхности пластичности и принцип градиентальности. В случае идеальной пластичности (отсутствия изотропного и кинематического упрочнения) аналогичный
принцип называется принципом максимума Мизеса [59]. В этом случае из условия экстремума функции Ф = N p – p f ( σ ), где р – неопределенный множитель Лагранжа, непосредственно следует ассоциированный закон течения [59].
Внекоторых случаях (например, при использовании условия пластичности Треска–Сен- Венана) принцип максимума формулируется в ослабленной форме, с заменой строгого неравенства на нестрогое:
σ : Dp σ : Dp . |
(4.37) |
Из ослабленного принципа Мазинга также следует принцип градиентальности, однако вместо условия выпуклости поверхности пластичности из него вытекает условие невогнутости последней.
Аналогичный принцип в пространстве скоростей деформаций был сформулирован Г. Циглером [65]. Вернемся к диссипативной функции (4.35). Для классической упругопластичности (нечувствительной к скорости деформации и опирающейся на понятие поверхности пластичности и принцип градиентальности) тензор напряжений не зависит от величины скорости деформации, он определяется предшествующей историей упругопластического
деформирования и направляющим (единичным) тензором Dp /| Dp | (| Dp |=( Dp : Dp )1/2). В силу этого диссипативная функция является однородной функцией первого порядка по
Dp . Напомним, что функция нескольких переменных f(x1, …, xn) называется однородной степени r, если f(kx1, …,k xn) = kr f(x1, …, xn). Для такой функции справедлива теорема Эйлера об однородных функциях, математическое выражение которой имеет вид:
x |
f |
+ ... + x |
|
f |
= r f(x |
,...., x |
|
) . |
|
|
n x |
|
|
||||||
1 |
x |
|
n |
1 |
|
n |
|
||
|
1 |
|
|
|
|
|
|
|
|
Тогда для диссипативной функции справедливо следующее представление:
N p = |
N p |
: Dp . |
(4.38) |
|
Dp |
||||
|
|
|
Сопоставляя (4.35) и (4.38), нетрудно установить соотношение
156
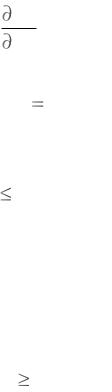
σ = |
N p |
, |
(4.39) |
Dp |
называемое в некоторых работах [14] ассоциированным законом нагружения. При фиксированной истории пластических деформаций уравнения
N p (Dp ) const |
(4.40) |
определяют в пространстве скоростей деформаций поверхности равного уровня диссипа-
тивной функции. Совокупность скоростей пластических деформаций D*p , удовлетворяющих при той же истории пластических деформаций соотношению
N p (D*p ) N p (Dp ) , |
(4.41) |
будем называть множеством допустимых скоростей пластических деформаций. Иначе говоря, если в пространстве скоростей пластических деформаций определена поверхность равного уровня диссипативной функции (4.40), то вектор возможных скоростей пластических деформаций расположен внутри объема, определенного данной поверхностью. Приведем формулировку принципа максимальной скорости диссипации [65]:
При фиксированной предыстории пластических деформаций из всех возможны ростей пластических деформаций (т.е. удовлетворяющих (4.41)) действительны рости пластических деформаций доставляют максимум диссипативной функции
σ : Dp σ : D*p . |
(4.42) |
Из последнего неравенства вытекает невогнутость (при строгом неравенстве выпуклость) поверхностей равного уровня диссипативной функции и (в случае одн родной первого порядка диссипативной функции) ассоциированный закон нагруж ния (4.39).
В работе [14] показана эквивалентность принципов максимума Мизеса (в пространстве напряжений) и Циглера (в пространстве скоростей пластических деформаций). Таким образом, два приведенных принципа дают альтернативные эквивалентные возможности формулировки ОС упругопластического тела.
Вопросы для самопроверки
1.Какие основные меры напряженного состояния применяются в теории пластичности и почему?
2.Запишите выражения для определения главных инвариантов тензора малых деформаций, девиаторов тензора напряжений Коши и тензора малых деформаций.
3.Приведите выражения интенсивностей напряжений, деформаций и скоростей деформаций.
4.Запишите соотношения для определения интенсивностей касательных напряжений, деформаций сдвига и скоростей деформаций сдвига. В чем их отличие от выражений интенсивностей напряжений, деформаций и скоростей деформаций?
5.Приведите запись тригонометрического представления главных значений девиаторов напряжений и деформаций.
6.Запишите параметр Надаи–Лоде для напряженного и деформированного состояний, объясните его механический смысл.
7.Приведите выражение параметра Надаи–Лоде через угол вида напряженного (деформированного) состояния, дайте его интерпретацию с использованием представления напряженного (деформированного) состояния на октаэдрической площадке.
8.Приведите соотношения для построения кругов Мора, дайте механическую интерпретацию диаграммы Мора.
157

9.Какие способы разложения мер деформации на упругую и пластическую составляющие Вам известны? Область применимости каждого из способов?
10.Запишите общий вид соотношения для определения поверхности пластичности. Какими свойствами, следующими из общего вида соотношения, обладает поверхность текучести?
11.Приведите критерии пластичности Треска–Сен Венана и Мизеса–Губера–Генки, дайте их объяснение с позиций механики деформируемого твердого тела.
12.Какие законы упрочнения Вам известны? Приведите их математическую запись.
13.Сформулируйте постулат Драккера и приведите его математическую запись.
14.Запишите локальный принцип максимума. Какие важные следствия вытекают из него?
15.Приведите формулировку постулата пластичности А.А.Ильюшина. В чем его отличия от постулата Драккера?
16.Сформулируйте принцип максимума Мазинга, приведите комментарии с позиций МДТТ.
17.Приведите формулировку принципа максимальной скорости диссипации Циглера. Какие следствия вытекают из него?
Теория производит тем большее впечатление, чем проще её предпосылки, чем разнообразнее предметы, которые она связывает, и чем шире область её применения.
|
А. Эйнштейн |
5. Теория упругопластических процессов |
А.А. |
Ильюшина |
|
Одной из наиболее глубоких теорий пластичности, нашедших широкое признание в ХХ веке, является теория упругопластических процессов (УПП) А.А. Ильюшина [10, 13, 17]. Несмотря на то, что исторически первыми появились теории пластического течения, изложение в настоящей работе в качестве первой именно теории УПП обусловлено широким использованием в современных теориях пластичности (включая и теорию пластического течения) понятий, определений, геометрической интерпретации, впервые введенных А.А. Ильюшиным.
Следует подчеркнуть, что в настоящем пособии рассматриваются только геометрически линейные теории пластичности, пригодные, строго говоря, только для процессов деформирования с малыми градиентами перемещений. С некоторыми проблемами, возникающими при рассмотрении деформирования с большими градиентами перемещений, можно познакомиться в [57].
Как и в большинстве других теорий, предполагается, что с достаточной обоснованностью может использоваться гипотеза о линейной связи первых инвариантов тензора напряжений Коши σ и тензора малых деформаций ε (или средних напряжений и деформаций
ε , 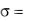 , K = E
, K = E (1 2ν) – модуль объемного сжатия, Е – модуль упругости, ν – коэффициент Пуассона). В связи с этим дальнейшее рассмотрение может быть сосредоточе-
(1 2ν) – модуль объемного сжатия, Е – модуль упругости, ν – коэффициент Пуассона). В связи с этим дальнейшее рассмотрение может быть сосредоточе-
но на связи девиаторных составляющих тензоров напряжений S и деформаций e . Как отмечено выше, в последние годы в работах по теории пластичности широко
используется предложенное А.А. Ильюшиным векторное (геометрическое) представление процесса деформирования (нагружения). С чем связана распространенность такого представления? Казалось бы, пятимерное векторное пространство так же трудно воспринимаемо, как и соответствующее девиаторное пространство. Однако в настоящее время реализуемыми экспериментально являются только процессы деформирования в трехмерном
189

пространстве (см. гл. 2), в котором наглядность векторного представления процесса очевидна. В случае теоретического анализа для большей размерности пространства используются векторные представления в нескольких двух- и трехмерных подпространствах пятимерного пространства, также обладающие большой наглядностью.
Согласно этому представлению, пяти независимым компонентам девиатора деформаций eij (напряжений Sij ), определенным в некоторой выбранной лабораторной системе координат (обычно – декартовой ортогональной), во взаимно однозначное (линейное) соответствие ставятся пять компонент вектора деформаций эi (напряжений i), которые относят к векторам ортонормированного, фиксированного в соответствующем пространстве (де-
формаций или напряжений) базиса ai |
|
|
|
|
|
|||
|
( i |
1,5). Векторы деформаций э и напряжений |
||||||
определяются как |
|
|
|
|
|
|
|
|
|
э э ai |
, |
Σ |
|
Σ |
ai , |
(5.1) |
|
|
i |
|
|
|
|
i |
|
|
э Э(5), |
(5), Э(5) и (5) – пятимерные векторные пространства деформаций и напряже- |
|||||||
ний соответственно. Отметим, что линейное соответствие e ~ э , S ~ Σ выбирается
обычно таким образом, что модули |
э |
и |
|
векторов деформаций и напряжений равны |
|
|
|
|
|
соответственно интенсивностям деформаций εu и напряжений и. В этом случае связь
компонент векторов напряжений и деформаций с компонентами соответствующих девиаторов может быть выражена, например, следующими соотношениями:
Σ1 = |
3 cos(β + |
6 |
)S11 |
|
|
3 sinβS22 , |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Σ2 = |
|
3 sin(β + |
6 |
)S11 |
|
|
3 cosβS22 , |
|
|
|
(5.2) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Σ3 = |
3S12 , |
Σ4 = |
|
3S23 |
, Σ5 = |
3S31, |
|
|
|
|
|
||||||||||||||||
э = 2 |
|
|
|
cos(β + |
6 |
)e |
|
|
|
2 |
|
|
sinβ e |
|
|
, |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
1 |
3 |
|
|
|
11 |
|
|
|
3 |
|
|
|
|
22 |
|
|
|
||||||||||
э = 2 |
|
|
|
|
sin(β + |
6 |
)e |
|
+ |
2 |
|
|
cosβ e |
|
|
, |
(5.3) |
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
2 |
3 |
|
|
|
11 |
|
|
|
3 |
|
|
|
|
|
22 |
|
|
||||||||||
э = 2 |
|
|
|
|
e , |
э = |
2 |
|
|
|
|
e |
|
, э = 2 |
|
|
e |
|
|
. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
3 |
3 |
12 |
4 |
|
3 |
|
|
|
23 |
5 |
|
3 |
|
31 |
|
||||||||||||
Инвертируя (5.2) и (5.3), получаем соответственно следующие соотношения:
S |
= 2 |
cosβ Σ |
|
|
2 |
sinβ Σ , |
|
|
|
|
|
|
||||||||
11 |
3 |
|
|
|
1 |
|
3 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
S |
= -sin(β + |
6 |
)Σ |
2 |
3 |
cos(β + |
6 |
) Σ , |
|
(5.4) |
||||||||||
22 |
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
S = 1 |
|
|
Σ |
, S = |
1 |
|
|
Σ |
4 |
, S = |
1 |
|
Σ |
, |
||||||
|
|
|
|
|
||||||||||||||||
12 |
|
3 |
3 |
|
|
23 |
|
3 |
|
31 |
|
3 |
|
5 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
190
