Теория определяющих соотношений. Часть 2. Теория пластичности

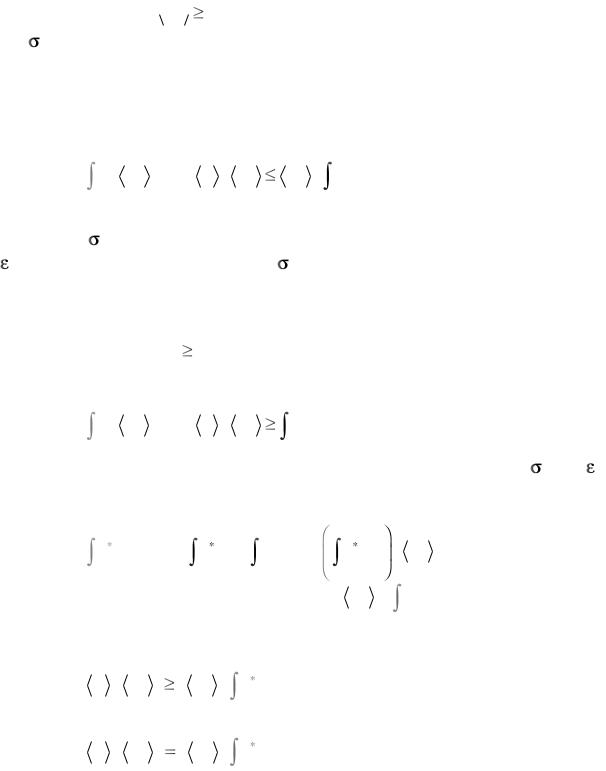
ляются действительными. Тогда согласно принципу максимальной работы для каждого монокристалла можно записать

σ * -σ : dε 0 , (8.47)

где – равновесные микронапряжения, действующие в поликр и- сталле и являющиеся допустимыми (действительные напряжения не нарушают условия текучести).

Интегрируя (8.47) по объему единичного куба, учитывая (8.46) и возможность вынесения из-под знака интеграла осредненных величин, получаем

допустимого, поскольку он также не нарушает условия текучести. Следовательно, для каждого из зерен справедливо неравенство принципа максимальной работы, записанное в форме

Полагая, что отсутствует корреляция между полями * и d в объеме единичного куба, правую часть (8.50) можно преобразовать следующим образом:

предположении непрерывности и гладкости соответствующих п о- лей перемещений du. Следовательно, из (8.50) и (8.51) вытекает

V

являющееся основным для построения функции текучести пол и- кристалла. Соотношение (8.53) представляет собой математическое выражение теоремы, сформулированной Бишопом и Хиллом в работе [67, 68]:

Действительная работа, производимая над поликр и- сталлическим агрегатом, равна работе, которую необходимо

271

совершить над отдельными зернами, составляющими агр е- гат, чтобы все зерна испытали микродеформации, равные макроскопической деформации поликристаллического пре д- ставительного объема.

Кратко рассмотрим процедуру построения поверхности тек у- чести, не вдаваясь в детали ее установления для конкретных типов поликристаллических агрегатов.

Построение поверхности текучести (по аналогии с её эксп е- риментальным определением) осуществляется перебором всех возможных направлений приращений пластических деформаций <d >. Для любого заданного < d >, рассматриваемого как свобо д- ный вектор в пространстве напряжений, для отдельн ых зерен определяются геометрически возможные векторы сдвига. Полагая известными к данному моменту деформирования накопленные сдвиги, а следовательно — критические напряжения сдвига в си с- темах скольжения, для каждого из зерен определяются напряжения

* , доставляющие максимальные значения работе в каждом зерне на приращениях микродеформаций, равных приращениям средних

брать» вершины многогранника поверхности текучести для кажд о- го из зерен и выбрать из них значение *, доставляющее максимум элементарной работе.

Отметим, что, хотя для построения поверхности текучести в данный момент нагружения не требуется определять приращения сдвигов в системах скольжения, для установления критических напряжений сдвига на следующем шаге нагружения необходимо иметь информацию о накопленны х сдвигах. В связи с этим после определения * устанавливаются физически и геометрически д о- пустимые векторы сдвига, определяемые с помощью принципа м и- нимума сдвига.

В результате решения указанной задачи оптимизации для к а- ждого зерна определяется величина *, а отсюда для любого за-

272

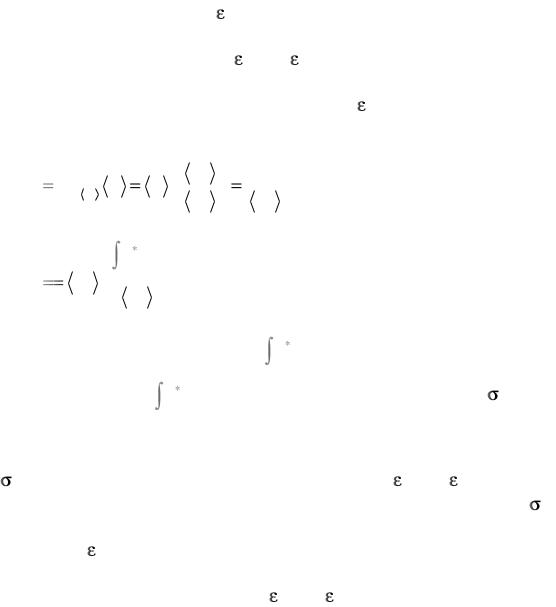
причем для заданного <d > величина dP – постоянная, уравнение (8.55) определяет гиперплоскость в пространстве напряж е- ний с «единичной нормалью» < d >/|<d >|. Иначе говоря, (8.55) определяет геометрическое место концов «вектора напряжений», с о- ответствующих приращению деформаций < d >. Кратчайшее расстояние от начала координат в пространстве напряжений до г и- перплоскости, определенной соотношением (8.55)

V

В соответствии с принципом градиентальности дл я поликристаллического агрегата для произвольной точки поверхности тек у- чести < > внешняя нормаль к ней совпадает с < d >/|<d >|, т.е. касательная к поверхности текучести гиперплоскость в точке < > совпадает с определенной выше гиперплоскостью (8.55) для любого заданного <d >. Отсюда следует, что поверхность текучести определяется как огибающая гиперплоскостей (8.55), построенных для всех возможных направлений < d >/|<d >|.

Напомним, что, поскольку «пробные» деформации имеют н у- левую гидростатическую составляющую, поверхность текучести является цилиндрической с образующей, направленн ой вдоль гидростатической оси. Для построения этой поверхности достаточно определить направляющую на девиаторной плоскости.

Отметим, что в случае изотропного поликристаллического агрегата поверхность текучести представляет собой круговой ц и- линдр. В этом случае достаточно определить его радиус для люб о- го направления в девиаторной плоскости. Для изотропии матери а- ла «в целом» требуется так называемая статистическая одноро д- ность. Последняя выполняется, если в каждом из зерен упрочнение полагается одинаковым на каждой из систем скольжения, а сами зерна имеют хаотическую ориентацию (ориентация распределена по равномерному закону).

Из рассмотрения модели нетрудно видеть, что наиболее тр у- доемкой её составляющей является построение поверхности тек у-

273

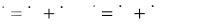
чести на каждом шаге нагружения. При современном развитии в ы- числительной техники данную процедуру можно исключить из а л- горитма решения конкретных задач. Действительно, для решения можно воспользоваться законом Гука в качестве ОС, в котором приращения пластических деформац ий на каждом шаге нагружения определяются непосредственно из модели Бишопа –Хилла.

Сопоставляя модель Бишопа –Хилла с ранее изложенной моделью Тейлора, нетрудно убедиться, что концептуальные полож е- ния обеих моделей практически совпадают (а следовательно , модели Бишопа–Хилла присущи те же недостатки, что и модели Те й- лора), однако модель Бишопа –Хилла отличается более глубокой «математической оснащенностью». Вероятно, это является прич и- ной того, что в последнее десятилетие модели, имеющие в основе те же гипотезы и положения, что и модель Тейлора, стали наз ы- вать моделями «типа Тейлора –Бишопа–Хилла». Модели этого тапа в последние 20 лет весьма широко используются при решении практически важных задач, в частности для описания формиров а- ния и эволюции микроструктуры.

Модель Линя

В большинстве работ по физической теории пластичности в качестве одного из основных недостатков моделей Тейлора, Биш о- па–Хилла и их модификаций отмечается неучет упругих деформ а- ций. Т.Г. Линь полагал [47, 70], что упруг ими деформациями можно пренебречь в случае больших пластических деформаций, что недопустимо в ситуации, когда эти составляющие имеют один п о- рядок. Однако подобная ситуация при анализе упругопластическ о- го деформирования представляет ограниченный интерес даж е в теоретическом плане и весьма редко встреча ется в практически важных задачах. Тем не менее включение в рассмотрение упругих деформаций представляется необходимым исходя из потребности определения остаточных напряжений (второго рода), во многом определяющих прочностные характеристики материала, и нака п- ливаемой упругой энергии. Отметим, что первоначально модель Линя сформулирована для случая малых деформаций.

Модель Линя базируется на следующих основных гипотезах . Скорости полных деформаций поликристалличе ского агрега-

та представляются суммой упругих и пластических составляющих

ε εe εp , e ee ep . (8.57)

274

Скорости полных деформаций отдельных зерен поликриста л- ла ε(n) (n = 1,2,…, N) равны скоростям полных деформаций пол и-

кристаллического агрегата:

ε(n) = ε = D, e(n) = e = d . (8.58)

Пластические деформации являются изохорическими, изменение объема определяется первым инвариантом упругих д е- формаций.

Пластические деформации обусловлены сдвигом по криста л- лографическим системам скольжения и подчиняются закону Шм и- да.

Упрочнение изотропно и определяется суммарным сдвигом по всем активным системам скольжения.

Рассмотрим соотношения для произвольно выбранного зерна. При наличии одной активной системы скольжения k скорость

сдвига γ(k ) в ней связана со скоростью пластической деформаци и

При активизации нескольких систем скольжения девиатор пластической деформации определяется выражением

K

dp = M(k ) γ(k ) , (8.60)

k =1

где K – число активных систем скольжения.

В соответствии с последней гипотезой критические с двиговые напряжения в каждой системе скольжения одинаковы и зав и- сят от суммарного сдвига:

где f (.) – производная функции f по накопленному сдвигу.

Скорости упругих деформаций в зерне определяются соотн о- шением

k=1

Впредположении изотропии упругих характеристик (отм е-

тим, что эта гипотеза может быть принята только в первом пр и- ближении) скорость изменения девиатора напряжений определяется согласно (изотропного) закон у Гука:

275

S = 2Gde . (8.64)

Скорость изменения шаровой части тензора напряжений (или среднего напряжения σ ) определяется также согласно закону Гука:

Заметим, что в случае исследования процессов с большими градиентами перемещений (т.е. геометрически нелинейных) мат е- риальная производная девиатора напряжений в (8.64) может быть заменена на производную, не зависящую от выбора системы о т- счета (чаще всего – коротационную [57]).

Рассмотрим процесс нагружения в пространстве девиаторов деформаций. Определение шаровых составляющих тензоров д е- формаций и напряжений осуществляется аналогично рассмотре н- ному ранее. Для решения (физически и/или геометрически) нел и- нейных задач, как правило, необходимо использовать пошаговые процедуры, согласно которым весь интервал нагружения разбивается на ряд малых шагов (приращений нагрузки или перемещ е- ний).

Рассматривается представительный макрообъем поликр и- сталлического агрегата. В начальный момент материал полагается находящимся в естественной конфигурации, в силу че го все компоненты тензоров напряжений и деформаций равны нулю; орие н- тации всех СС полагаются заданными (тем или иным законом ра с- пределения). Для представительного объема полагается заданным закон нагружения (т.е. заданы все компоненты тензора деформ а- ции как функции времени (или возрастающего параметра), а сл е- довательно, в каждый момент нагружения известны компоненты тензора деформации скорости).

На первом шаге материал является упругим; задавая тензор деформации скорости перемещений в соответстви и с (8.64) и учитывая, что de = d , определяется скорость изменения девиатора н а- пряжений. Интегрируя, по последней определяется момент дост и- жения в одной из СС (например, с номером 1) сдвигового напряжения, равного по модулю начальному критическому напряжению ,

c 0 = f(0). После этого момента начинается неупругое скольжение по системе 1 при возрастающем девиаторе деформации e (последний определяется интегрированием d). При этом в кажд ый момент деформирования должно выполняться условие пластического т е- чения

τ(1) = τc = f(γ(1) ) ,

или

2GM(1) : (e M(1)γ(1) ) = f(γ(1) ) . (8.66)

276

При заданном в каждый момент времени е (8.66) представляет собой уравнение для определения γ(1) .

При выполнении (8.66) и возрастающем девиаторе деформации e (в каждый момент времени определяемого интегрированием d с использованием любой из известных схем) одиночный сдвиг продолжается до тех пор, пока в некоторой другой системе скол ь- жения (например, 2) сдвиговое напряжение ( 2 ) не достигнет критического значения τc = f(γ(1) ) . Начиная с этого момента, возраст а-

ние e вызывает двойное скольжение по системам 1 и 2, при этом должны выполняться следующие условия:

(8.67)

(8.67) – система двух алгебраических уравнений для определения

γ(1) , γ(2) .

Аналогичным образом рассматривается вовлечение в скол ь- жение 3-й, 4-й и 5-й систем скольжения. При этом на каждой из активных систем скольжения должно выполняться условие текуч е- сти. При продолжающемся активном деформировании возможно возникновение ситуации, когда условие текучести выполняется одновременно более чем в пяти системах скольжения (при испол ь- зовании закона типа шмидовского для ГЦК -кристаллов это соответствует нахождению ИТН в одной из вершин, где пересекаются 6 или 8 гиперплоскостей). В этом случае, опираясь на экспериментально известный факт о некотором превышении латентного у п- рочнения над деформационным (активным), предпочтение отдают ранее вовлеченным в скольжение системам.

В конкретных расчетах обычно используют систему уравн е- ний типа (8.67), записанную в приращениях, например вида:

j

всем активным системам скольжения (в том числе и бывшим а к- тивными ранее, в текущий момент деформирования перешедших в разряд пассивных).

Для перехода к модели поликристалла используется один из известных подходов к осреднению (чаще всего – ориентационное осреднение).

277

Модель Линя по сравнению с ранее рассмотренными обладает тем преимуществом, что позволяет определять последовательность активных систем скольжения и учитывает упругие деформации. В то же время использование гипотезы Фойгта (об однородности полных деформаций в представительном микрообъеме) приводит к нарушению условий равновесия на границах зерен. В дальнейшем Линем и другими исследователями предпринимались и предпр и- нимаются попытки построения так называемых самосогласованных моделей пластичности поликристаллов, в которых выполняются как условия совместности деформаций, так и условия равновесия на границах зерен [47, 70]. В знач ительной мере эти исследования опираются на решение Эшелби задачи об одиночном эллиптич е- ском включении в бесконечной однородной упругой среде с э ф- фективными характеристиками[47]. В дальнейших исследованиях (Кренер, Хилл) были рассмотрены более сложные зад ачи об одиночном включении в упругопластической среде с эффективными (осредненными) характеристиками. Следует отметить, что самос о- гласованные модели требуют чрезвычайно больших вычислител ь- ных ресурсов.

Другим направлением развития физической теории являет ся модификация законов упрочнения и определение изменения п о- верхности текучести для монокристаллов с целью включения в них постоянно обновляющихся экспериментальных и теоретических данных об эволюции дислокационных субструктур. В последние 10–15 лет физическая теория активно применяется для описания процессов глубокого пластического деформирования, особое вн и- мание при этом уделяется анализу эволюции микроструктуры, в частности возникновению и развитию текстуры.

В заключение кратко остановимся на связи физи ческой теории с рассмотренной в главе 1 структурой конститутивной модели, основанной на введении внутренних переменных. Как нетрудно видеть, рассмотренные здесь различные модификации физической теории относятся к двухуровневым моделям, при этом основной целью является определение реакции материала на макроуровне. По существу, роль собственно определяющих соотношений играет закон Гука (обычно – в скоростной форме). Внутренней явной п е- ременной макроуровня является тензор пластической составля ю- щей деформации скорости. Внутренними неявными переменными являются критические напряжения сдвига по СС и скорости сдвига в последних. В качестве эволюционных уравнений выступают з а- коны упрочнения, связывающие скорости изменения критических напряжений со скоростями сдвиго в в СС. Наконец, замыкающими уравнениям являются соотношения, определяющие среднюю по

278

представительному макрообъему пластическую составляющую д е- формации скорости по скоростям сдвигов в СС.

В данной главе описаны главным образом основополагающие работы по физической теории пластичности. В последние годы и н- терес к ФТП резко возрастает, что находит отражение в огромном числе публикаций, посвященных различным аспектам теории. Как представляется, в ближайшие 5 –10 лет ФТП станет одной из наиболее применяемых тео рий для решения практически важных задач. Особую роль в этом процессе играет быстрое развитие вычи с- лительной техники и соответствующих методов, особенно – появление ЭВМ и методов параллельных вычислений.

Вопросы для самопроверки

1. В чем состоит основное отличие физической теории пластичности от математических теорий пластичности?

2. Какой механизм неупругого деформирования считается в ФТП основным и почему?

3. Запишите выражения для ориентационного тензора и зак о- на Шмида, приведите физическое обоснование последнего.

4. Какими соотношениями определяется поверхность текуч е- сти монокристалла? Для чего требуется удвоение числа систем скольжения по сравнению с числом кристаллографических СС?

5. На основе какого принципа устанавливаются ОС пласти ч- ности монокристалла? В чем трудность применения уравнения п о- верхности текучести (8.3)?

6. Какую роль играют границы зерен в процессах пластич е- ского деформирования поликристаллов?

7. Каковы основные гипотезы модели Закса?

8. Опишите алгоритм определения напряжения течения с и с- пользованием модели Закса. Назовите основные недостатки да н- ной модели.

9. Перечислите основные гипотезы, положенные в основу м о- дели Тейлора.

10. В чем состоит при нцип минимума сдвига Тейлора ? С чем связана необходимость его формулировки?

11. Приведите описание процедуры построения кривой одн о- осного деформирования, основанной на модели Тейлора.

12. Каким образом модель Тейлора может быть приведена к задаче линейного программирования?

13. Назовите основные недостатки модели Тейлора.

14. Сформулируйте основные положения, на которых базир у- ется модель Бишопа–Хилла на макроуровне.

279

15. Приведите основные гипотезы, принимаемые в модели Бишопа–Хилла на уровне монокристалла (зерна).

16. Сформулируйте и докажите принцип максимальности р а- боты для монокристалла.

17. Дайте определения геометрически возможных и физич е- ски возможных векторов сдвига.

18. Сформулируйте и докажите принцип минимума работы для монокристалла.

19. В чем состоят отличия между принципами минимума р а- боты и максимума работы ? Как они связаны между собой?

20. Сформулируйте гипотезы, использованные Бишопом и Хиллом для построения модели деформирования поликристалла, объясните их физический смысл и значение для мод ели.

21. Приведите графическую иллюстрацию осреднения прир а- щений деформаций с использованием соотношения (8.20), запишите соотношения для всех компонент тензора приращения деформаций, используя единичный куб и декартову ортогональную сист е- му координат.

22. Аналогично п.21 – для тензора напряжений Коши с и с- пользованием соотношения (8.23)1 .

23. Восстановите доказательство соотношения (8.30), объясните его важность для формулировки основных соотношений те о- рии Бишопа–Хилла.

24. Опишите процедуры построения огранич ивающих поверхность текучести цилиндрических поверхностей в модели Б и- шопа–Хилла.

25. Сформулируйте и докажите теорему Бишопа –Хилла (8.53)

.

26. Опишите процедуру построения поверхности текучести в теории Бишопа – Хилла.

27. Перечислите основные гипотезы модели Линя. В чем с о- стоит её основное отличие от модели Бишопа –Хилла?

28. Опишите процедуру применения модели Линя для иссл е- дования изменения напряженно -деформированного состояния представительного макрообъема.

29. Приведите основные направления развития современной физической теории пластичности.

30. Опишите связи между общей структурой конститутивной модели (см. гл.1) и ФТП Закса, Тейлора – Бишопа–Хилла и Линя.

280